三维等熵欧拉方程组解的爆破
2015-08-08朱旭生艾利娜汤传扬
朱旭生,艾利娜,汤传扬
(华东交通大学 理学院,江西 南昌 330013)
0 引言
考虑三维空间中带阻尼项等熵欧拉方程组:
(1)
的Cauchy问题,对应的初始数据为
(2)

对欧拉方程组的Cauchy问题解的研究已有很多,主要集中在经典解的整体存在性以及经典解爆破的研究.在文献[1]中,王维克和杨彤研究了带阻尼项的等熵欧拉方程组的初值问题,当初始数据是在一个常状态附件的小扰动时,得到了经典解的整体存在性.文献[2]研究了三维可压缩欧拉方程组的经典解,并用能量估计的方法证明了解的整体存在性.而文献[3]报道了有界区域内带阻尼项的可压缩欧拉方程组的初边值问题的经典解的整体存在.文献[4-5]报道了带阻尼项的等熵欧拉方程组,在假设某些初始数据较大时,构造泛函,得出经典解的爆破.文献[6-8]报道了真空状态下的欧拉方程组正规解的爆破.文献[9]考虑带有温度项的欧拉方程,引入特殊速度函数,进而研究欧拉方程的爆破现象.文献[10]充分利用了轴对称和理想气体状态方程的特点,当关于初始速度的泛函足够大时,经典解会在有限时间内爆破的结论.本文继续研究三维空间中带阻尼项的等熵Euler方程组的Cauchy问题,结合文献[4-6]中的方法,在M(0)<0条件下,当初始数据较大时,通过构造泛函,证明其经典解在有限时间内必定发生爆破的结论.
1 预备知识
定义:


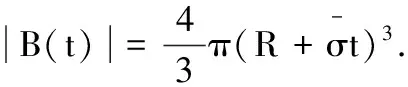
根据经典解的局部能量估计知道方程组的经典解具有有限传播速度的性质,即

2 主要结论
在M(0)<0条件下得到以下结论:

(3)
则τ 证明假设(ρ,u)是方程在时间区间[0,τ)的C1解,且T<τ,则由方程组(1)可得 则 M(t)=M(0). (4) 对F′(t)分部积分,由方程组(1)可得到 根据状态方程P=Aργ且γ>1,可得 所以 (5) 根据引理1和Cauchy-Schwartz不等式可得: (6) 又由式(4)可得 (7) 而A′(t)>0,即A(t)递增,从A(t)的定义可知A(0)>0,所以A(t)>0恒成立,从而综合式(5)、(6)和(7)可得以下微分不等式: (8) 可设G(t)=eαtF(t),则G′(t)=eαt(F′(t)+αF(t)),所以 (9) 而当0≤t≤T时,则 那么 (10) 而由F(0)=G(0),T<τ及式(3)得出: 即G′(t)>0.那么G(t)一定时间内是增加的,所以 那么得到: (11) 对式(11)在[0,t]上积分,可得到 而F(0)=G(0),所以 (12) 则τ 证明假设(ρ,u)是方程在时间区间[0,τ)的C1解,且T<τ,同样对F′(t)进行分部积分,得: |x|2x·▽P+ρ|x|2|u|2dx, 所以 F′(t)+αF(t)≥ (13) 根据引理1和Cauchy-Schwartz不等式可得到: (14) 又由式(7)可得 (15) 结合式(13)、(14)和(15)可得以下微分不等式 而由定理1可知A(t)>0且递增,所以 我们仍设G(t)=eαtF(t),则G′(t)=eαt(F′(t)+αF(t)),所以 (16) 而当0≤t≤T时,则 那么 (17) 同理,由F(0)=G(0),T<τ及式(12),得G′(0)>0,那么G(t)一定时间内是增加的,所以 那么 (18) 对式(18)在[0,t]上积分,可得到 由F(0)=G(0)及式(12)可得 对任意t∈[0,T]成立. 同理,再由定理1可得τ 本文在满足了一些条件的基础上,研究了三维等熵欧拉方程组的柯西问题,获得的主要结论是:在Sideris T.C.研究结果的基础上,当初始数据足够大时,运用泛函分析的方法,得到两种条件下,欧拉方程组经典解爆破的结论,分析过程清晰简单.本文虽然研究了等熵欧拉方程组在三维空间中经典解的爆破问题,而对于在一维、二维空间的研究没有涉及,所以今后有待于研究的是运用本文中的方法,解决一维、二维空间中,等熵欧拉方程组经典解的爆破问题.
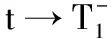
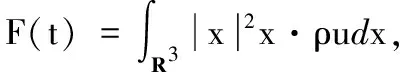
3 结语
