地面超载对土钉墙工作性能影响的有限元分析
2015-08-08张宗领
张宗领,付 超
(信阳师范学院 土木工程学院,河南 信阳 464000)
0 引言
土钉支护是近年来基坑工程中广泛应用的一种用于土体开挖和边坡稳定的挡土技术,由被加固土体、深入土体的钢管或钢筋(土钉)、钢筋混凝土面层组成,形成一个类似重力式挡墙的结构,以此来抵抗开挖面后土体的压力和地面超载等,从而保持开挖面的稳定.其工作机理是在土体中放入一定长度和密度的土钉,这种加筋土较原状土的强度和刚度大大提高,从而显著提高开挖面的稳定.土钉支护结构的施工过程包括定位、成孔、置筋、注浆等工序.
虽然土钉支护具有安全可靠、施工便捷、成本较低等优点,在岩土工程界深受青睐[1].但目前对其理论研究远滞后于工程实践,很多土钉支护结构仅凭经验设计,工程事故时有发生,尤其在坑后地表存在地面超载的情况下,开挖面水平位移显著增大,更容易发生强度和稳定破坏.因此,研究在地面超载作用下土钉墙的受力和变形机理很有必要.
有限元法是对土钉支护结构进行理论分析较为流行的一种方法,不仅能分析支护结构的变形及受力,也能模拟基坑开挖、支护的施工过程[2].本文以某深基坑土钉支护结构为例,运用非线性有限元软件ADINA模拟了基坑开挖与支护的施工过程,分析了地面超载对土钉支护结构工作性能的影响.
1 土钉支护工程算例
某高层建筑深基坑,东西长约60 m,南北宽约30 m,开挖深度9 m.从上到下基坑各层土体参数见表1,根据基坑周边的环境和土质情况,结合以往的施工经验,垂直开挖并采取了土钉支护方案,设置了6排土钉,土钉倾角均为10°,采用梅花形布置,竖向间距1.5 m,水平间距1.3 m,钢筋直径均为22 mm,第一排距坑顶0.8 m,最后一排距坑底0.7 m,其中第一、二、三排的钉长为16 m,第四、五排的钉长为12 m,第六排的钉长为9 m.在坑壁钻直径为120 mm的孔,钢筋网采用∅10@250×250的钢筋,土钉之间采用∅14@1200×1200的加强钢筋纵横双向焊接,土钉端头采用钢板螺母加固,最后喷射100 mm厚的混凝土面层.
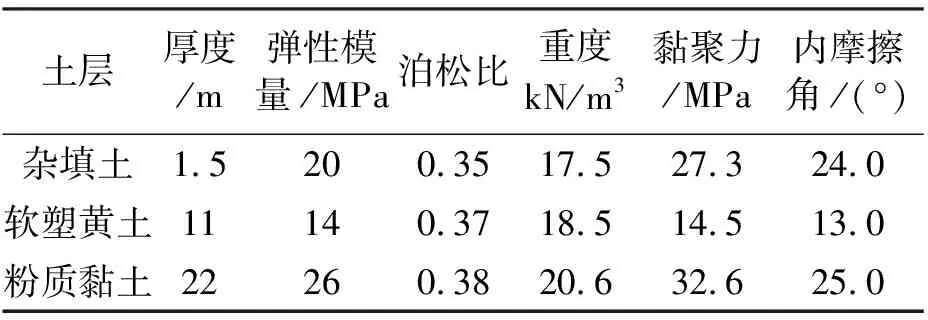
表1 基坑土体物理力学参数
2 有限元模型的建立
基于基坑的对称性,有限元分析时取整个基坑的1/4,根据文献[3]的结论并考虑以往的工程经验[3-8],基坑开挖对宽度的影响为3~4.5倍的挖深,对深度的影响为2~4倍的挖深,最终的整体三维有限元模型尺寸取70 m×55 m×36 m,如图1所示.

图1 整体三维有限元模型
在模型中,土体选用3D-solid8节点实体单元,被土钉加固的土体的力学行为极为复杂[9],采用Mohr-coulomb屈服准则描述其受荷后由弹性状态向塑性状态转变时的材料特性,其表达式为:
其中:σ1,σ3分别为最大和最小主应力;c,φ分别为土体的黏聚力和内摩擦角;土钉采用杆单元(rebar单元),按弹性材料考虑,其弹性模量按混凝土和钢筋的截面积进行加权计算,同时考虑钉、土间的极限摩阻力进行修正;钢筋混凝土面层按弹性材料考虑,3D-solid8节点实体单元.
施工过程的模拟是利用了ADINA中的单元“生死”功能,“杀死”即把土体开挖掉,刚度、质量为零;“出生”即支护,刚度、质量荷载等将恢复其原始的数值.基坑施工工程采取分步开挖和支护,共分6步,每步挖深均为1.5 m.为了使有限元分析结果能反映真实的施工情况,模拟的开挖和支护步数、每步的挖深均与实际施工过程相同.
3 地面超载影响的有限元分析
为了研究坑后地面超载对土钉支护结构受力和变形的影响,从开挖面到坑后20 m的范围内施加水平均布荷载q,分别取q=0、15、30 kPa时分析其对开挖面水平位移、坑后地面沉降、坑底隆起以及各排土钉轴力的影响.
3.1 地面超载对开挖面水平位移的影响
图2给出了开挖结束后不同地面超载情况下中部开挖面上沿深度方向的水平位移.由图2可知,地面超载不仅影响开挖深度以上土体的水平位移,也影响了坑底下部土体的水平位移.当超载为0、15、30 kPa时最大水平位移分别为23、30、36 mm,有超载比无超载最大水平位移分别增大30.4%和56.5%.水平位移随地面超载的增大而增大,且二者增量间近似呈线性关系.

图2 不同地面超载下的开挖面水平位移
3.2 地面超载对坑后地面沉降的影响
图3给出了开挖结束后不同地面超载情况下坑后的地表沉降.
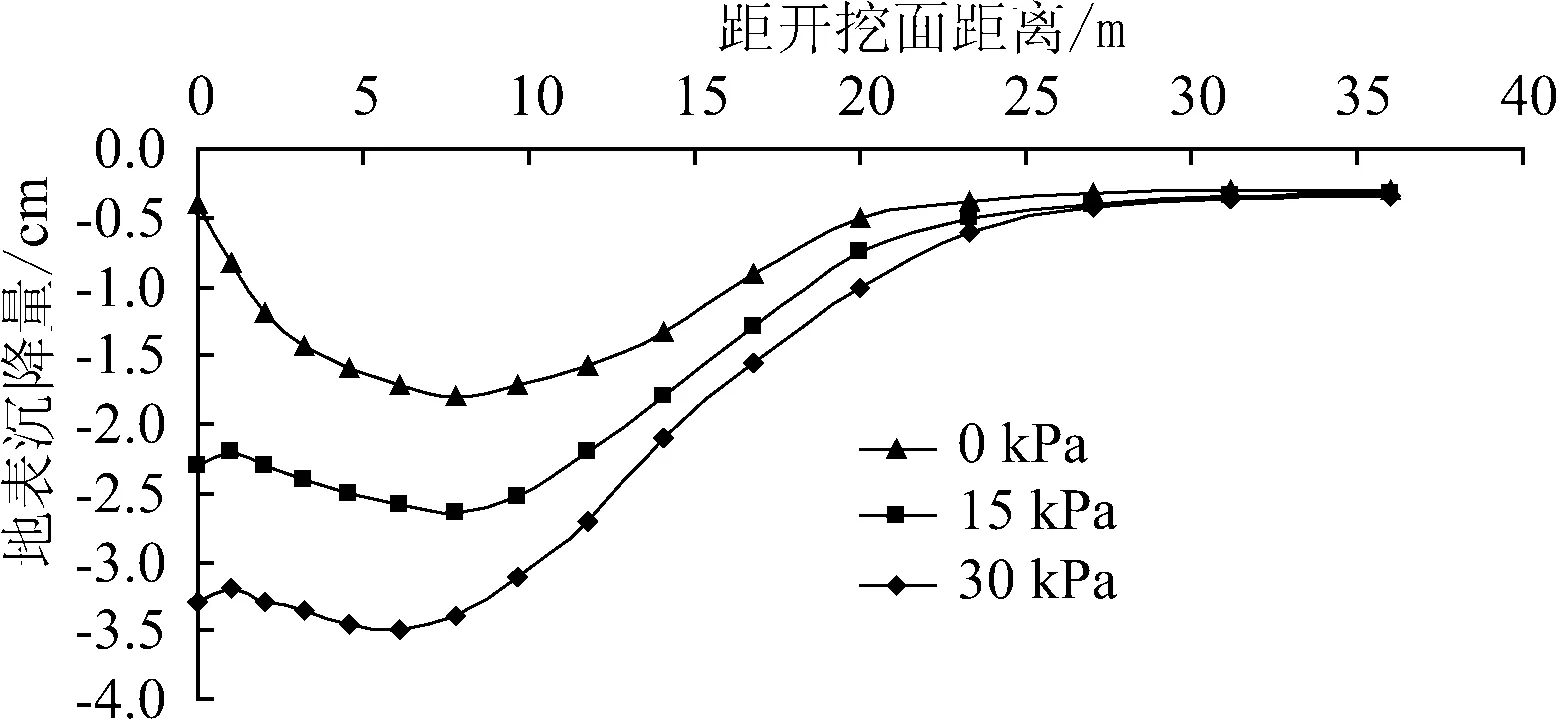
图3 不同地面超载下的地面沉降
由图3可知,在加载范围内,地面超载对坑后地面沉降的影响较大,在加载范围外,地面超载对坑后地面沉降的影响较小.当超载为0、15、30 kPa时坑后最大沉降值分别为1.8、2.65、3.4 cm,有超载比无超载最大地面沉降分别增大47.2%和88.9%.
无超载时沉降曲线呈“勺子”形状,有超载时沉降曲线前端接近水平(靠近开挖面处),有无超载最大沉降值均出现在距开挖面约1倍挖深处,地面沉降随地面超载的增大而增大,且二者增量间近似呈线性关系.
3.3 地面超载对坑底隆起的影响
图4给出了开挖结束后不同地面超载情况下基坑中心线上坑底的隆起值.由图4可见,地面超载对坑底隆起的影响较小,可忽略不计.
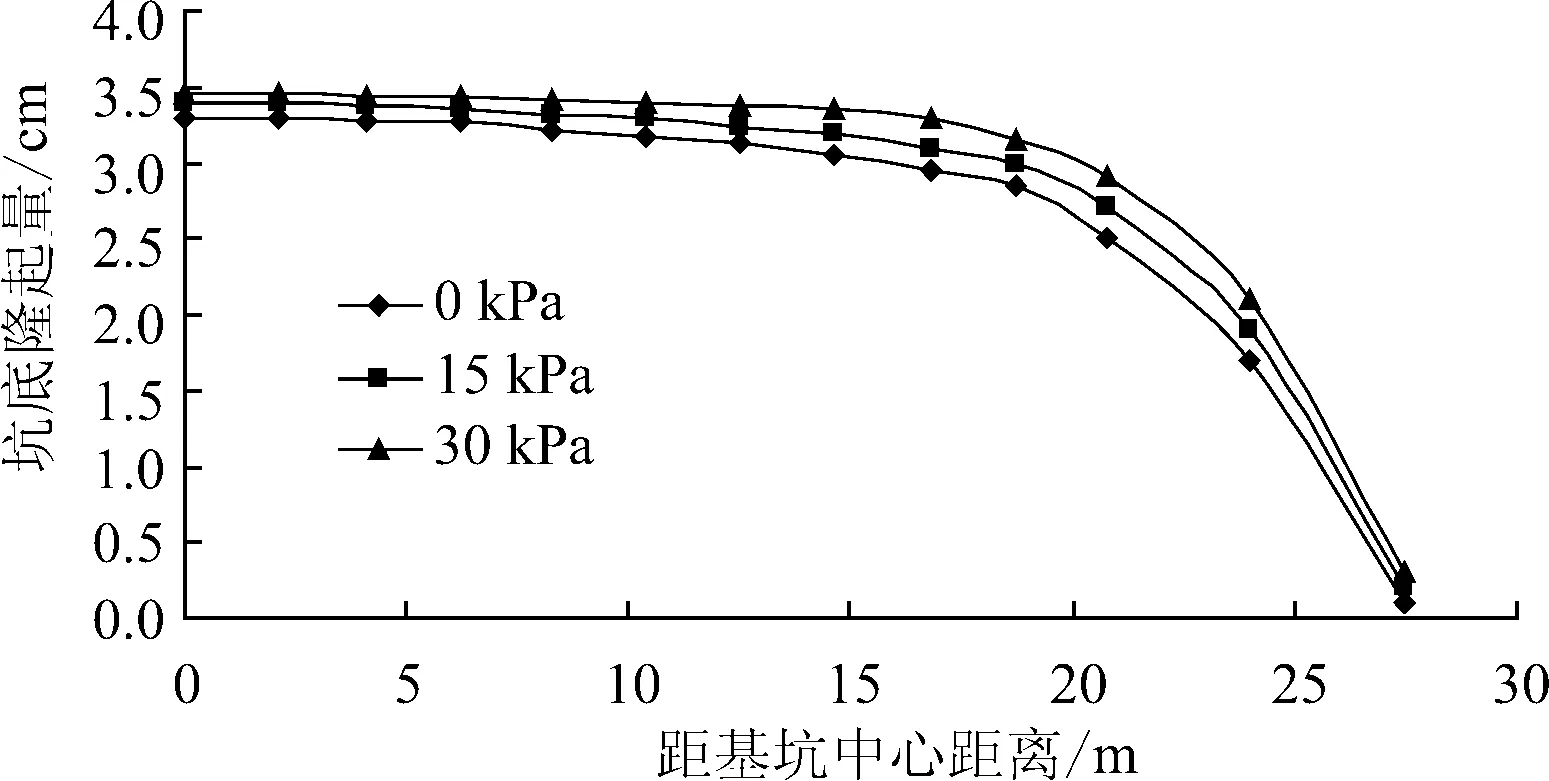
图4 不同地面超载下的坑底隆起
3.4 地面超载对各排土钉轴力的影响
图5~图7分别给出了开挖结束后不同地面超载情况下第二、四、六排的土钉轴力.从图中可以看到,有无地面超载轴力曲线形状基本相同,仍呈两头小、中间大的枣核形,随着地面超载的增大,每排土钉的轴力都在增大.上部土钉轴力的增大幅度大于下部土钉轴力的增大幅度,且从上往下,轴力峰值逐渐从土钉中后部转移到前部,峰值的连线预示着潜在的滑移面位置.总的来说,由于超载施加在地表,对上部各排土钉轴力的影响要大于下部.
4 结语
随着地面超载的增大,开挖面的水平位移、坑后地面沉降均随之增大,且近似呈线性关系,但坑底隆起变化不大.在加载范围内,地面超载对坑后地面沉降的影响较大,在加载范围外,地面超载对坑后地面沉降的影响较小,无超载时沉降曲线呈“勺子”形状,有超载时沉降曲线前端接近水平,有无超载最大沉降值均出现在距开挖面约1倍挖深处.随着地面超载的增大,每排土钉的轴力都在增大,地面超载对上部各排土钉轴力的影响要大于下部各排.
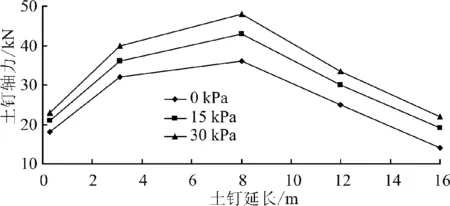
图5 不同地面超载下的第二排土钉轴力

图6 不同地面超载下的第四排土钉轴力
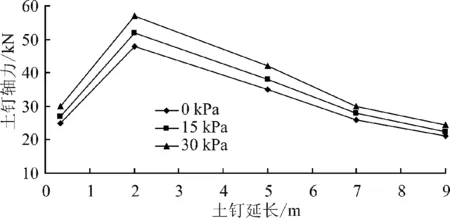
图7 不同地面超载下的第六排土钉轴力
