一类病毒动力学模型的全局稳定性

郑丽丽,王 娟

(信阳师范学院 数学与信息科学学院, 河南 信阳 464000)

0 引言

近年来，有关1型人类免疫缺陷病毒(HIV-1)和丙型肝炎病毒(HCV)动态模型的建立与研究备受关注,并得到了许多很好的结果[1-3].1型人类免疫缺陷病毒感染过程可以通过如下简单微分方程模型描述[3]:

(1)

其中:T(t),I(t)和V(t)分别表示t时刻未受感染的靶细胞、感染HIV病毒的靶细胞及HIV-1病毒数;s表示新靶细胞的生成率;d表示未感染的靶细胞的自然死亡率;δ是受感染的靶细胞的死亡率;受感染的靶细胞以比率q生成自由病毒;参数c表示HIV-1病毒被体内免疫系统吞噬的比例.假设HIV-1感染靶细胞服从双线性发生率,即kT(t)V(t).所有的参数都是正常数.文献[4]已证明模型的全局动力学性态完全由基本再生数决定.基于系统(1),一些作者研究了具有非线性发生率的病毒动力学模型[5-7].

文献[8]讨论了以下具有比率依赖接触率的HIV-1动力学模型：

(2)

文献[8]中讨论了模型(2)解的有界性、平衡点的局部稳定性及系统的持续性等，给出了病毒消失或持续的阈值条件，但没有讨论感染性平衡点的全局渐近稳定性.研究免疫系统感染平衡点或传染病系统的地方病平衡点的全局渐近稳定性是很有意义的问题.本文将讨论模型(2)的全局稳定性问题，给出了系统感染平衡点全局稳定的充分条件.

1 系统(2)的全局性分析

直接计算可得系统(2)的基本再生数表达式为

(3)

下面两个定理见文献[8].

定理1 系统(2)的解(T(t),I(t),V(t))是非负有界的.

定理2 如果R0>1，则系统(2)是持续的.

本文主要目的是依据文献[9-11]中的方法，证明系统感染平衡点E2是全局渐近稳定的.特别地，我们将论证系统(2)的全局稳定性.

通过计算系统(2)的雅可比矩阵，取矩阵H为H=diag(1,-1,1),容易看出系统(2)在凸区域Ω中,关于定义在象限{(T,I,V)∈R3:T≥0,I≤0,V≥0}中的偏序是竞争系统.为了证明我们的结果，需要以下引理.

引理1[10-11]假设D是凸有界的且系统

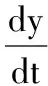
(4)

由引理1和文献[8]中的定理4,可以得到下面主要结果.

定理3 假设：

(H1)R0>1,

和下列两个条件中的一个成立：

则系统(2)的正平衡点E2是全局渐近稳定的.

证明假设ρ(t)=(T(t),I(t),V(t))是系统(2)的周期解,且其轨道γ包含在Ω内.显然，由定理1和定理2，对所有的t≥0,T(t),I(t)和V(t)都是具有下界的有界函数.系统(2)关于周期轨道γ的雅可比矩阵为：

(5)

这里，

与系统(2)的周期解ρ(t)=(T(t),I(t),V(t))相关第二个加性复合系统为：

(6)

根据文献[10]中的定理6.3,定义以下Lyapunov函数：

L(t)=L(Y1(t),Y2(t),Y3(t),T(t),I(t),V(t))=

(7)

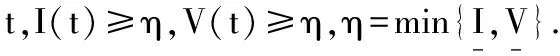
L(Y1,Y2,Y3;T,I,V)≥c1sup{|Y1|,|Y2|+|Y3|}.

(8)

L(t)的右导数存在，直接计算得：

D+|Y1(t)|≤-(δ-Q11)|Y1(t)|+

D+|Y2(t)|≤q|Y1(t)|-(c-Q11)|Y2(t)|,

D+|Y3(t)|≤mQ13|Y2(t)|-(δ+c)|Y3(t)|.

因此,我们得到

D+L(t)≤sup{h1(t),h2(t)}L(t),

(9)

其中

重写系统(2)中的后两个方程：

从而

(10)

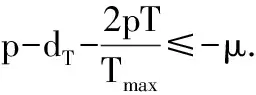
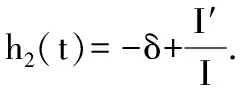
(11)

令ω=min{μ,δ}，由式(10)和(11)得

由式(9)和Gronwall不等式，得L(t)≤L(0)I(t)e-ωt≤L(0)Me-ωt.这意味着L(t)→0，t→+∞.通过式(8)得

L(Y1(t),Y2(t),Y3(t))→0,t→+∞.

这意味着线性系统(6)是渐近稳定的，因此周期解是渐近轨道稳定的.根据引理1，知系统(2)的正平衡点E2是全局渐近稳定的.证毕.

定理4 假设(H1)和(H2)成立.若(H3)不成立，则系统(2)存在轨道渐近稳定的周期解.

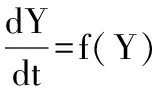
这里，

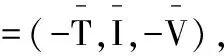
2 结论

进一步研究了具有比率依赖接触率的病毒动力学模型的全局稳定性.运用竞争系统的结果，证明了当系统是持久的，而正平衡点不稳定时，存在一个轨道渐近稳定的周期轨道.利用复合矩阵和周期轨道的稳定性,得到了正平衡点全局稳定性的充分条件.