基于连续介质力学模型的部分埋入单桩的纵向振动研究

刘林超，冯震宇，闫 盼，陈晴晴

(1.信阳师范学院 土木工程学院, 河南 信阳 464000;2.国网信阳供电公司, 河南 信阳 464000 )

0 引 言

桩基础在建筑、铁路、公路等基础工程领域有着广泛的应用，桩基通常要承受纵向、水平、扭转等动态激励，所以对于桩基振动特点的研究具有十分重要的意义，国内外不少学者对完全埋入桩基的振动特性进行了系统的研究[1-6].鉴于高速铁路、码头工程、离岸结构和输油栈线等结构的基础大都采用部分埋入式桩基[7]，李炳球等[8]给出了部分埋入弹性地基中变截面桩自振频率和振型的数值计算方法.任青等[9-11]利用Winkler 动力梁模型和传递矩阵法研究了部分埋入单桩竖向振动问题，并采用有限元子结构方法，提出可以考虑承台板对部分埋入式群桩动力阻抗贡献的计算方法.Catal H H[12]在考虑弯矩、轴力和剪力的情况下研究了半刚性连接的部分埋入桩的自由振动.

目前对桩-土动力相互作用的研究主要采用连续介质力学模型、Winkler动力梁模型和数值方法.Winkler动力梁模型计算简单，与实际结果较为接近，但需要通过实验、边界元和有限元等方法确定模型参数，而数值计算方法研究桩-土动力相互作用计算量较大.连续介质力学模型是将桩周土介质视为连续体，基于连续介质理论和框架来建立桩基力学行为的数学模型，其中，桩和土的材料可以是弹性、黏弹性和弹塑性材料等，在一定的简化假定下，可较精确揭示桩-土间的相互作用.连续介质力学模型具有理论性强、概念清楚等优点.为了准确地反应桩-土之间的相互作用，本文拟采用连续介质力学模型研究部分埋入式单桩的纵向振动问题.

1 土层竖向振动

考察图1所示土中的部分埋入式单桩，桩顶作用有竖向简谐集中荷载，简谐荷载的频率为ω，埋入土中桩的长度为l1，伸出土体外的桩长为l2，桩底为基岩，桩的直径为d，桩身混凝土密度为ρp.由于伸出部分桩长较大或者竖向动力荷载较大时，单桩将会出现明显的压曲现象[13]，这里假定伸出部分桩的长度和竖向动荷载没有达到导致桩发生屈曲的情况，并假定土体材料阻尼采用振频无关的滞回阻尼形；土层上表面为自由边界，无正应力和剪应力；桩土系统振动为小变形谐和振动，桩土接触界面两侧位移、应力连续.

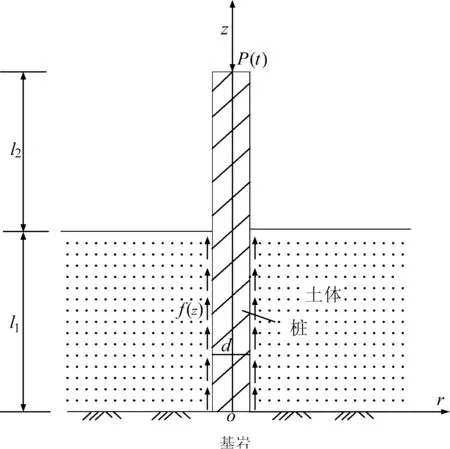
图1 部分埋入单桩计算模型

(1)

(2)

其中:ρ为土体的密度;λ，μ为土体的拉梅常数.

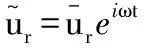
(3)

(4)

其中，

η1n=mkK0(k/2)+βm2εK0(β/2)+

mkK1(k/2)+β3εK1(β/2)，

η2n=-qK0(k/2)-β2εK0(β/2)，

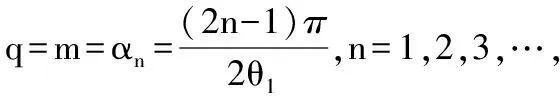
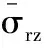
2 部分埋入单桩的竖向振动

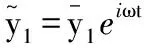
(5)

(6)

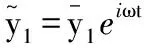
(7)

(8)

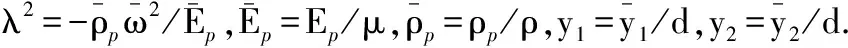
(9)

(10)

这里E1、E2、E3、E4为待定系数.

考虑土体中和土体外桩的连续条件以及桩底和桩顶的边界条件，则有

(11)

其中:θ2=l2/d，P为无量纲化后的桩顶集中简谐荷载的幅值.考虑边界条件式(11)、式(9)和式(10)可得

E1+E2=0,

(12)

E1eλθ1+E2e-λθ1+

E3eλθ1+E4e-λθ1,

(13)

E1eλθ1-E2e-λθ1=E3eλθ1-E4e-λθ1,

(14)

(15)

(16)

由式(12)—式(16)可得

(17)

(18)

-(e-λ(θ1+θ2)+eλ(θ1+θ2))·

(19)

(e-λ(θ1+θ2)+eλ(θ1+θ2))θ1B1m·

(20)

可以看出，式(20)为无穷维线性方程，求解式(20)可以确定系数B1n(n=1,2,3,…)，再由式(12)—式(16)可以求得E1、E2、E3和E4，从而可以求出部分埋入式单桩的纵向振动位移的表达式，则桩顶的纵向位移为

(21)

桩顶产生单位竖向位移时的桩顶竖向荷载即为桩顶竖向复刚度，由此可得桩顶竖向复刚度为

(22)

3 数值分析与讨论

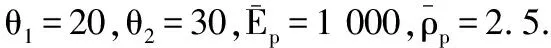
图2和图3分析了桩的埋入深度和桩土模量比对桩顶纵向复刚度的影响.可以看出，桩顶纵向复刚度的实部和虚部随无量纲频率dω/vs的变化曲线存在明显的波峰和波谷，而且随频率的增大峰值越大，由此可见动态简谐荷载作用下桩-土体系存在共振现象.可以看出，在埋入深度不变(θ1不变)的情况下，当外露部分桩长小于埋入部分桩长时，桩顶纵向复刚度随频率变化曲线波动较为平稳.当外露部分桩长大于等于埋入部分桩长时，桩顶纵向复刚度随频率变化曲线波动较大，且外露部分桩长较埋入部分桩长越大波动越厉害，可能是由于外露部分过长时土体对外露部分桩基没有约束，稳定性相对较差的缘故.可见对桩基进行设计时，尽量减少外露部分的桩长.桩土模量比对部分埋入单桩纵向振动也有较大的影响，桩土模量比越大，桩顶纵向复刚度越大，且桩顶竖向复刚度随频率变化曲线峰值对应的频率越大.可见我们可以通过改变桩土模量比也改善部分埋入桩基的抗震性能.

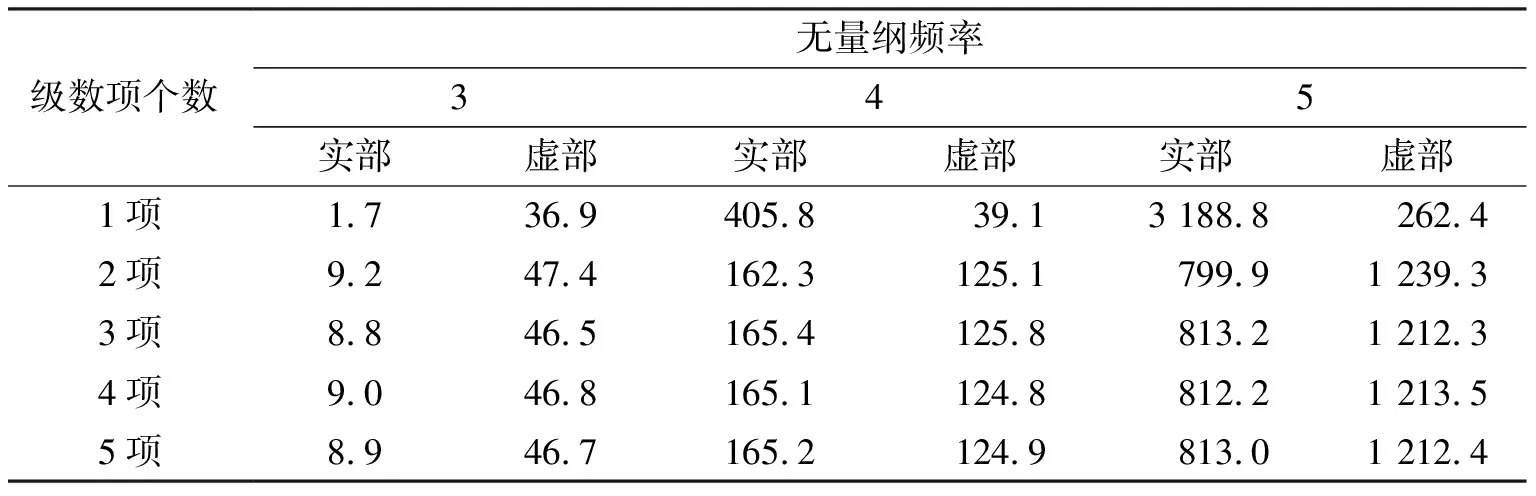
表1 数值结果的收敛性

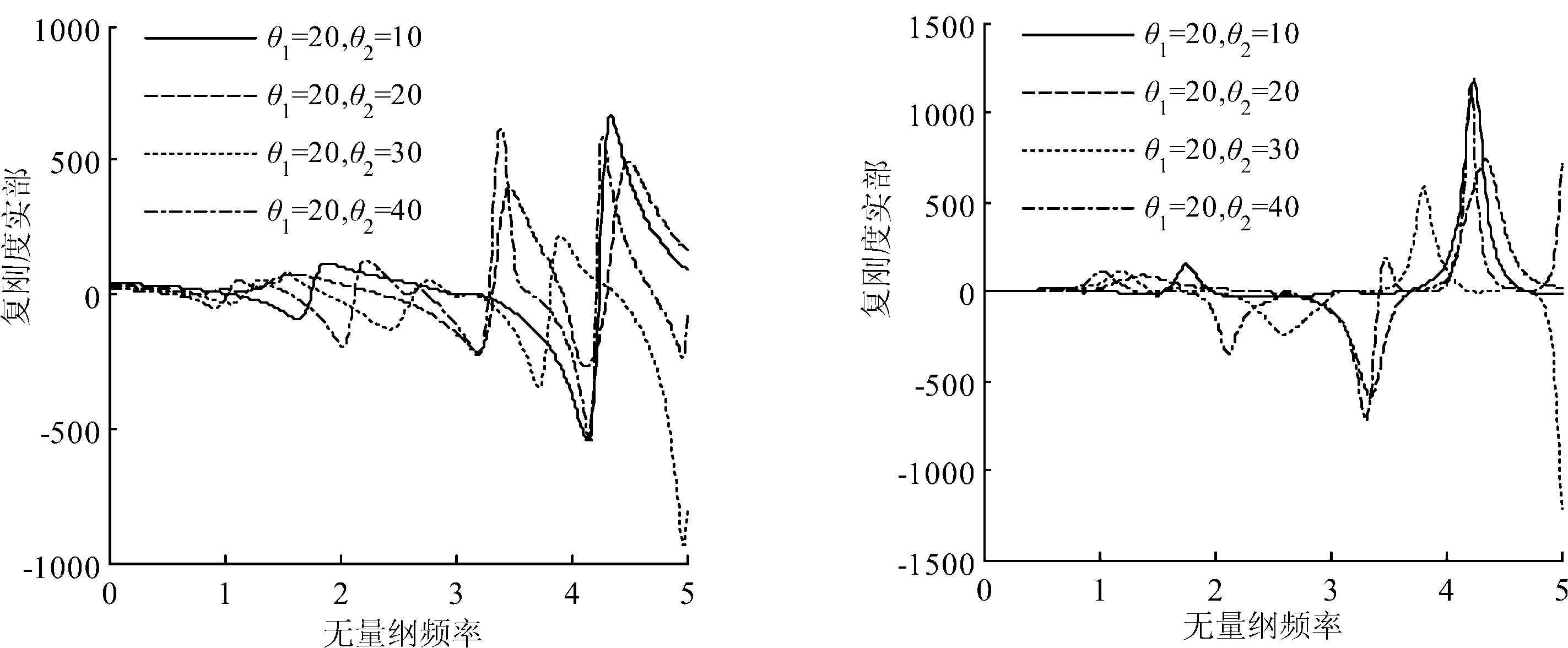
(a)复刚度实部 (b)复刚度虚部

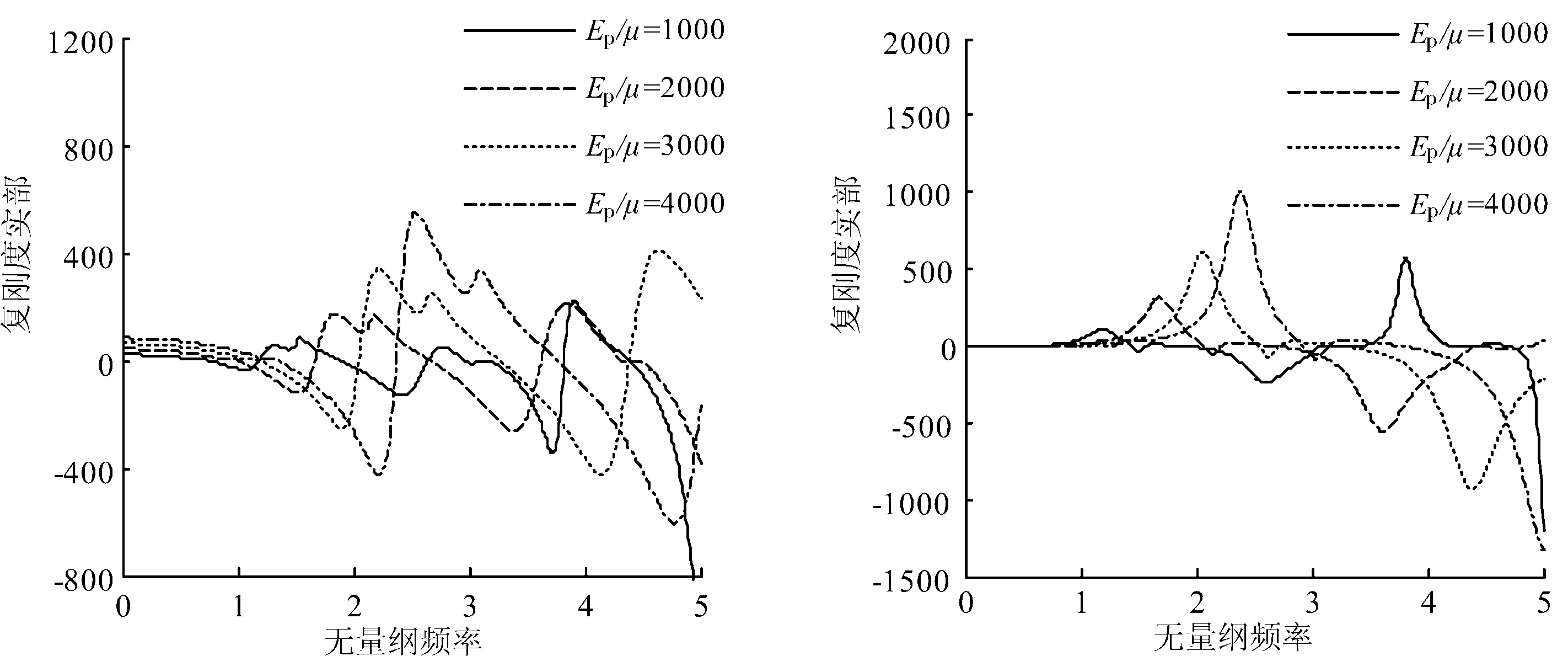
(a)复刚度实部 (b)复刚度虚部

4 结语

以部分埋式单桩的纵向振动为研究对象，将桩基视为杆件单元，考虑桩土之间的连续条件和桩基与土体的边界条件得到了部分埋入单桩的桩顶复刚度.对于桩顶复刚度的级数解，只需取前几项即可满足计算精度的要求；桩的埋入深度和桩土模量比对部分埋入单桩的竖向振动的影响较大，且外露部分桩长与埋入部分桩长之比对桩顶复刚度随频率变化曲线的波动情况有较大影响.为了减小这种波动，设计时尽量较少外露部分的桩长.