城市无信号控制T型交叉口通行能力计算方法
2015-08-07李爱增王啸啸李文权
李爱增,王啸啸,李文权
(1.河南城建学院交通运输工程学院,河南,平顶山467036;2.东南大学交通学院,南京210096)
城市无信号控制T型交叉口通行能力计算方法
李爱增*1,王啸啸1,李文权2
(1.河南城建学院交通运输工程学院,河南,平顶山467036;2.东南大学交通学院,南京210096)
以当量人群描述非机动车和行人对机动车通行的共同影响,对城市无信号控制T型交叉口的交通流运行优先等级进行重新划分,共划分为5级.将主路直行车流和横穿支路的当量人群流作为独立优先流,应用间隙接受理论,研究了各次级交通流的可能通行能力计算方法.考虑高等级次级交通流及横穿主路的当量人群流的影响,采用概率论方法研究了各次级交通流的可能通行能力修正系数,从而得到各次级交通流的实际通行能力计算模型,进而得到整个无信号控制T型交叉口的通行能力计算方法.结果表明,以当量人群描述非机动车和行人对机动车通行的共同影响计算过程简单,符合我国城市道路交叉口非机动车和行人多的实际情况.
交通工程;城市无信号控制T型交叉口;通行能力;间隙接受理论;概率论;当量人群;优先等级
1 引言
对城市无信号控制T型交叉口的通行能力进行分析是制定交叉口管理和控制策略、交叉口设计,以及进行城市道路网通行能力分析等的基础.目前,有较多文献对无信号控制T型交叉口的通行能力进行研究[1-8],也有文献对T型交叉口禁左的交通量条件[9]进行分析.上述研究中,大部分是基于可接受间隙理论进行分析,也有部分文献基于交通仿真的方法进行研究.然而,上述研究中大部分没有分析非机动车和行人对机动车通行的影响[1-4],也有部分文献只对行人对机动车通行的影响进行了分析[5,6].与国外相比,我国城市道路交叉口的显著特征是交叉口处具有较多的非机动车和行人,它们相互作用对机动车的通行构成了影响[10].对非机动车和行人影响的分析成为我国城市道路无信号控制T型交叉口通行能力计算的关键.为了分析这种影响,国内也有少数学者采用时间占有率法以修正系数的形式体现非机动车和行人对机动车通行能力的影响[8,9].
本文以当量人群描述非机动车和行人对机动车通行的共同影响.研究过程中,对横穿支路的当量人群流作为机动车流的独立优先流进行分析,对横穿主路的当量人群流采用概率论方法以修正系数的方法进行分析,从而得到符合我国实际的城市无信号控制T型交叉口通行能力计算方法.
2 城市道路交叉口当量人群运行特征
非机动车和行人在通过交叉口的过程中,相互之间相距较近而且存在着一定的交叉.以当量人群描述非机动车和行人对机动车通行的共同影响,研究表明,当量人群的群时距服从移位负指数分布,并且当量人群的个数和群时距与当量人群的当量人数之间存在着式(1)和式(2)所示的关系[10].

式中yg为15 min时段当量人群个数;x为15 min时段当量人数.
当量人数指的是在指定的时间段内,根据自行车、电瓶车和行人间的换算系数值,即1.67、1.58和1,将自行车和电瓶车换算为行人后的“人数和”.
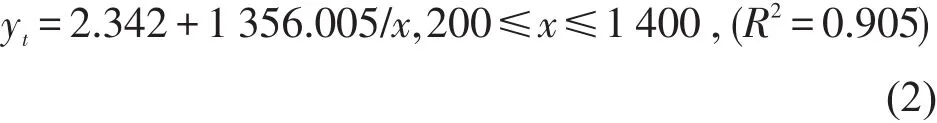
式中yt为15 min时段平均群时距(s).
3 T型交叉口交通流运行优先等级
不同学者对无信号控制T型交叉口的交通流运行优先等级划分也不尽相同.王炜等划分的公路无信号控制T型交叉口交通流运行优先等级如图1所示[4];陈吉发划分的交通流运行优先等级如图2所示[8];HCM2000划分的交通流运行优先等级如图3所示[5].
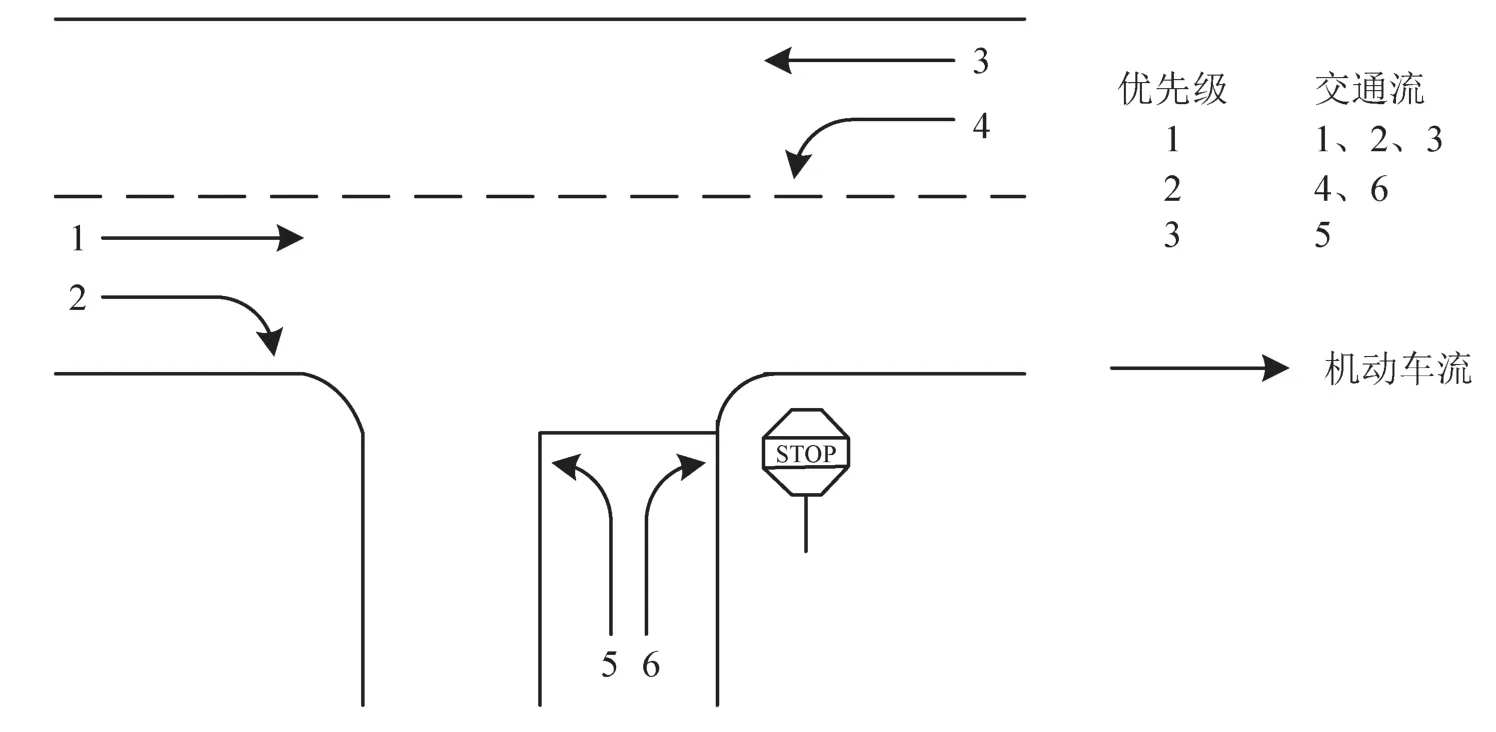
图1 王炜划分的交通流运行优先等级Fig.1 Priority ranks of traffic flows divided by Wang-Wei
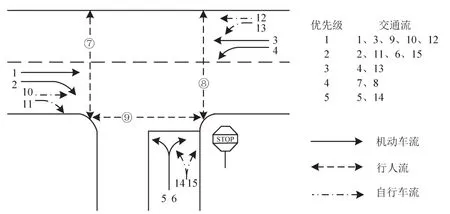
图2 陈吉发划分的交通流运行优先等级Fig.2 Priority ranks of traffic flows divided by Chen Ji-fa

图3 HCM2000划分的交通流运行优先等级Fig.3 Priority ranks of traffic flows divided by HCM2000
上述交通流运行优先等级划分中,以美国HCM2000的划分标准最具代表性.但国外交叉口中,由于非机动车交通量很小,因此国外的研究成果一般最多只考虑了行人流,而我国则不同.将城市道路交叉口处,非机动车和行人对机动车通行的影响以当量人群进行描述,本文对城市无信号控制T型交叉口的交通运行优先等级划分如图4所示.
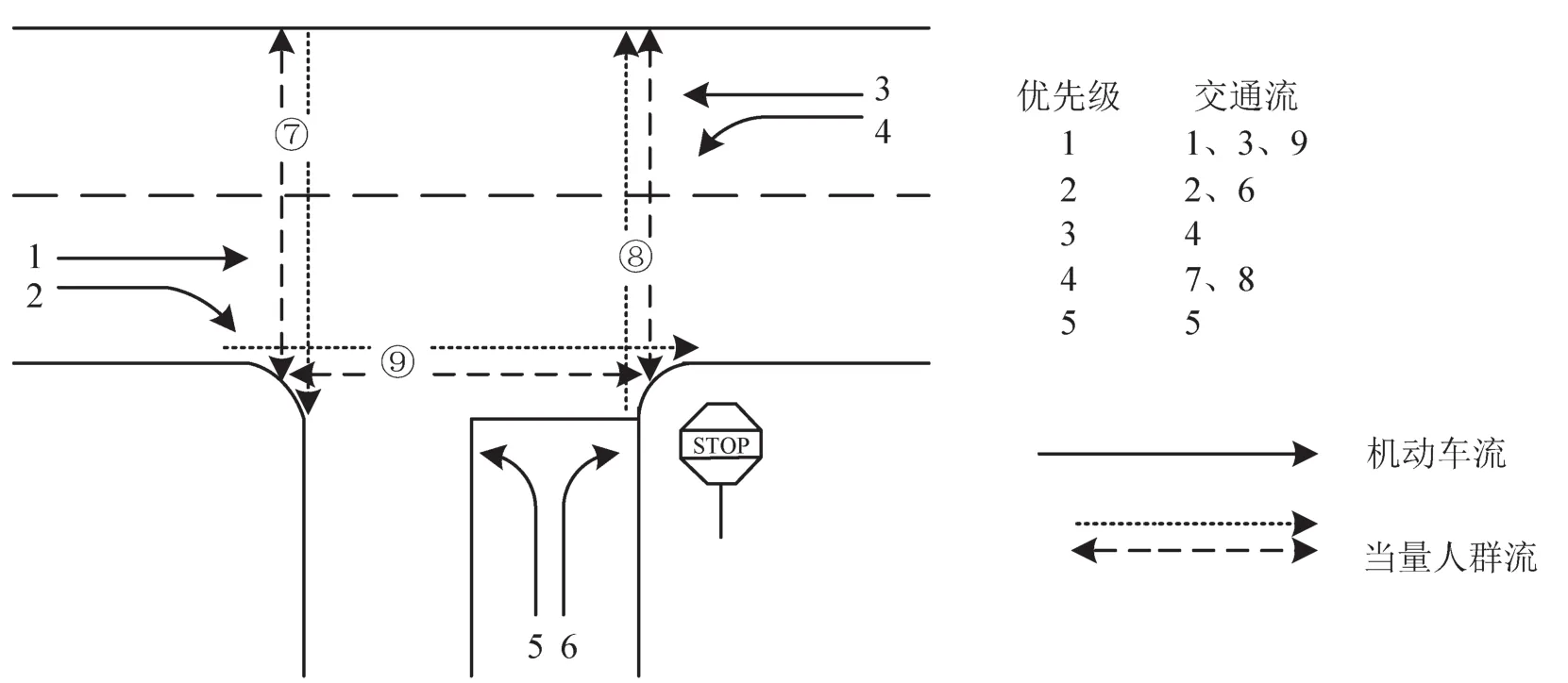
图4 城市无信号控制T型交叉口交通流运行优先等级Fig.4 Priority ranks of traffic flows on urban road unsignalized T-intersection
4 城市道路交叉口交通流到达特性
对无信号控制T型交叉口的通行能力进行分析,应用较多的是间隙接受理论,首先需要确定主路交通流的到达分布规律.研究表明[11],当距上游信号交叉口在400 m以内时,下游交叉口车辆的到达车头时距服从M3分布;当距上游信号交叉口大于400 m时,如果到达下游交叉口的交通量小于500 veh/h,到达车头时距服从移位负指数分布,如果到达交通量大于500 veh/h,到达车头时距服从M3分布.对于城市道路交叉口处当量人群的到达特性,研究表明[10],当量人群的群时距服从移位负指数分布.
5 城市T型交叉口通行能力计算
根据T型交叉口的交通流运行优先等级划分,次要交通流的优先流中有一部分为独立优先流,即在一组优先流中,各交通流优先等级相同,相互独立,彼此不需要让行.本文下述研究将依据第一优先等级的独立优先流计算各次级交通流的可能通行能力,对于高等级次级交通流对低等级次级交通流的影响将以修正系数的方法进行分析.根据上述交通流运行优先等级划分,横穿次路的当量人群流将作为独立优先流进行分析,横穿主路的当量人群流将以修正系数的方法进行通行能力修正.
5.1 次级交通流的可能通行能力
由于横穿支路的当量人群流具有第一优先等级,因此,对于任何次级交通流来说,除了主路右转只有具有移位负指数分布的单优先流(即横穿支路的当量人群流)外,其它任何次级交通流的独立优先流都是当量人群流与机动车流的组合.所以,除了主路右转次级交通流外,其它所有次级交通流的多重独立优先流的车头时距分布组合可能是:移位负指数分布(当量人群流)+移位负指数分布(机动车流)、移位负指数分布(当量人群流)+M3分布(机动车流)、移位负指数分布(当量人群流)+移位负指数分布(机动车流)+M3分布(机动车流).下面分析独立优先流服从不同分布时次级交通流的可能通行能力.
(1)移位负指数分布(当量人群流).
当次级交通流k只需穿越符合移位负指数分布的当量人群流时,利用间隙接受理论,可以得到次级交通流的可能通行能力计算公式如式(3)所示.

式中tc为次级交通流车辆穿越冲突流时的临界间隙(s);tf为次级交通流的随车时距(s);ts为冲突交通流的最小时距(s);qe为当量人群流流量(群/h);θ为尺度参数,θ=qe/(3 600-qets);R(t)为主路车头时距分布的残存函数(survivor function)[6],R(t)=1-F(t),其中F(t)为主路车头时距的分布函数.
(2)移位负指数分布(当量人群流)+移位负指数分布(机动车流).
此种情况下,利用间隙接受理论,可以建立次级交通流的可能通行能力计算公式如式(4)所示.
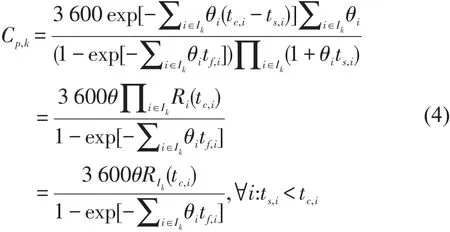
式中Ik为次级交通流k的独立优先交通流的集合;θi为交通流i的尺度参数;kk为主路多重独立优先流叠加过程中延迟分布的残存函数;tc,i、tf,i为次路车辆穿越交通流i的临界间隙(s)和随车时距(s);ts,i为交通流i的最小车头时距(s).
(3)移位负指数分布(当量人群流)+M3分布(机动车流).
当当量人群的到达时距服从移位负指数分布时,令其属于Ik1系列,当机动车流的到达车头时距服从M3分布时,令其属于Ik2系列.文献[8]利用间隙接受理论,推导了独立优先流分别服从移位负指数分布和M3分布时次级交通流的可能通行能力计算公式,如式(5)所示.
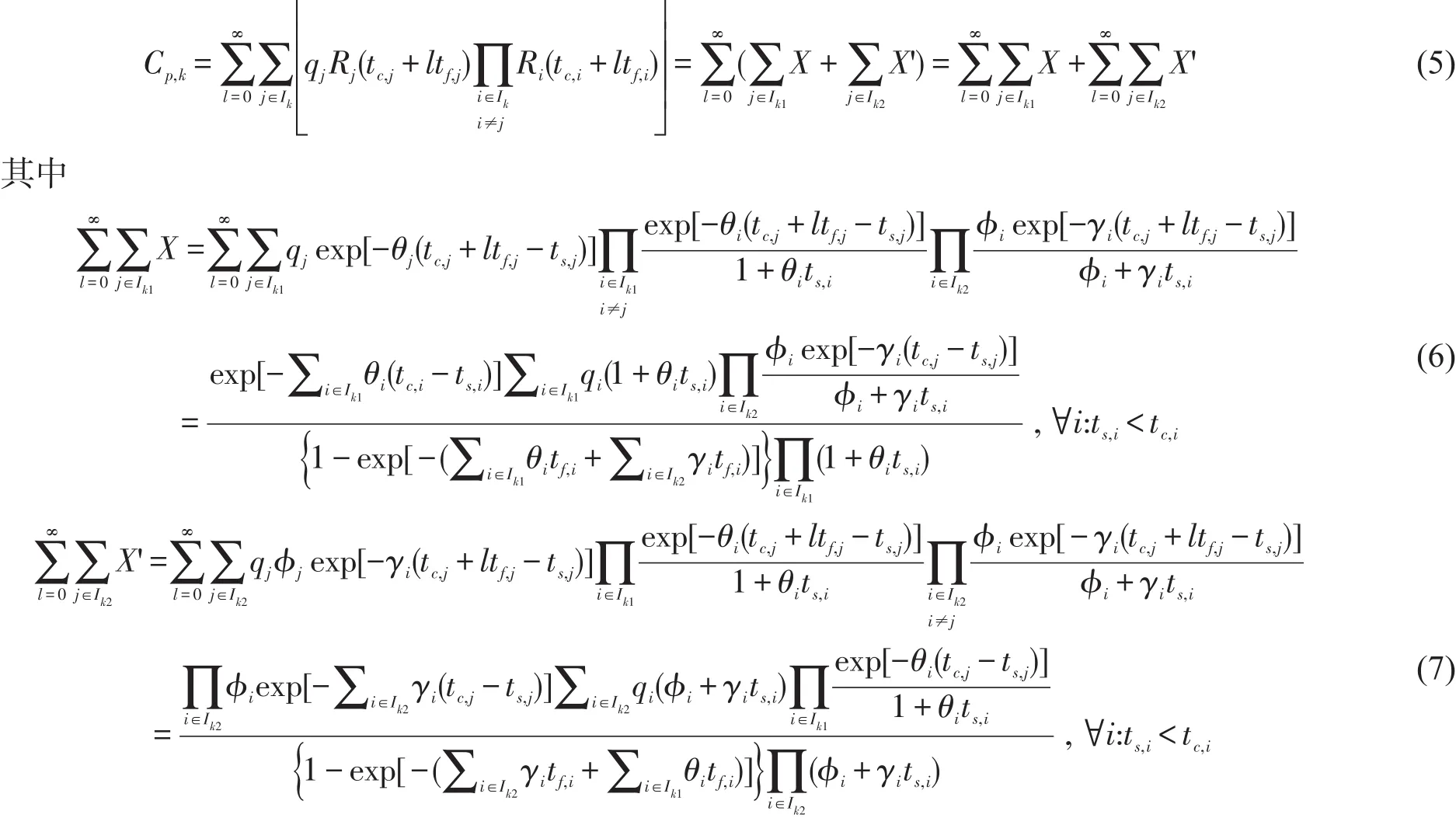
式中qi为交通流i的交通流率(pcu/h);φi为交通流i的自由流比例;γi=qiφi/(3 600-qits,i)为交通流i的衰减常量.
(4)移位负指数分布(当量人群流)+移位负指数分布(机动车流)+M3分布(机动车流).
此种情况下,仍可运用式(5)~式(7)对次级交通流的可能通行能力进行分析,但由于机动车流穿越当量人群流和机动车流时的临界间隙和随车时距不同,因此在对Ik1系列进行计算时,针对二者的临界间隙和随车时距取不同的值.
5.2 次级交通流的实际通行能力
5.2.1 机动车流间的阻抗影响分析
(1)应用间隙接受理论计算交叉口的通行能力时,总是假设第一优先等级的交通流(主路直行:1、3)不受其它次级交通流的影响,它的最大通行能力受道路条件的限制.
(2)对于第二优先等级的交通流(主、次路右转:2、6)来说,它必须让行且只需让行于第一优先等级的交通流.因此第二优先等级交通流的实际通行能力等于其可能通行能力,即

式中b为第二优先等级交通流,b=2、6.
(3)对于第三优先等级(主路左转:4)的交通流来说,它除了需让行于第一优先等级的交通流外,还要让行于第二优先等级的主路右转交通流2.对于第二优先等级的交通流2来说,其进入交叉口时无排队的概率为

式中V2为交通流2的交通流率(pcu/h).
因此,对于第三优先等级交通流4来说,其通行能力修正系数为

式中d为第三优先等级交通流,d=4.
由上述分析,得第三优先等级交通流的实际通行能力计算公式如式(11)所示.

(4)对于第五优先等级的交通流(次路左转:5)来说,它除了需要让行于第一优先等级的交通流外,还需要让行于第三优先等级的主路左转交通流4.主路左转交通流4进入交叉口时无排队的概率为

式中V4为交通流4的交通流率(pcu/h).
因此,对于第五优先等级的交通流5来说,其通行能力修正系数为

式中n为第五优先等级交通流,n=5.
得次路左转交通流5 的实际通行能力计算公示如式(14)所示

5.2.2 当量人群流的阻抗影响分析
横穿支路的当量人群流⑨具有第一优先等级,其对次级交通流的影响体现在各次级交通流的可能通行能力中.对于横穿主路的当量人群流⑦,次路左转交通流⑤必须让行.
当量人群流⑦出现可穿越间隙的概率为

式中tc′为次路左转机动车流穿越当量人群流的临界间隙(s);λ′为移位负指数分布参数,λ′=1/(ˉt-tm′),ˉt为当量人群的平均群时距(s),可由式(2)进行计算;ts′为当量人群的最小群时距(s),可取ts′=1 s.
因此,对于当量人群流⑦来说,其对机动车流5的阻抗系数可由式(16)进行计算.

因此,考虑当量人群流影响的次路左转交通流5的实际通行能力C′m,5如式(17)所示.
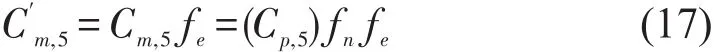
5.2.3 共用车道情况下的通行能力分析
上述通行能力分析隐含的假设是各流向交通流具有专用车道,实际情况中,往往存在着不同流向交通流共用车道的情况,尤其是次路交通流.
(1)次路入口共用车道情况.
次路入口共用车道时的通行能力计算可采用HCM2000的分析方法[18],如式(18)所示.

式中Csh为共用车道的实际通行能力(pcu/h);Vy为共用车道中流向y的交通流率(pcu/h);Cm,y为共用车道中流向y的实际通行能力(pcu/h).
(2)主路入口共用车道情况.
当主路入口左右转车流和直行车流共用车道时,左右转车流也可能由于等待可接受间隙而影响主路直行车流的通行.此种情况下,在实际通行能力计算中可用式(19)和式(20)计算的代替前文的p0,2、p0,4,以考虑左右转车辆排队对主路直行车流的影响.
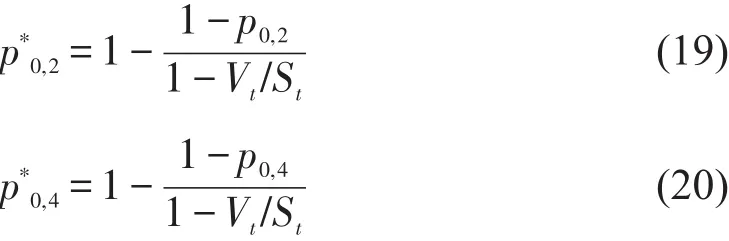
式中Vt为主路直行车流流率(pcu/h);St为主路直行车流饱和流率(pcu/h).
6 算例分析
图5所示为河南省平顶山市的光明路—启蒙路无信号T型交叉口,该交叉口的早高峰小时交通量如图6所示.

图5 T型交叉口现状图Fig.5Schematic diagram of T-intersection
经调查,该交叉口南进口内侧车道的车头时距服从M3分布,φ=0.83,其它车道的车头时距服从移位负指数分布.交叉口次级交通流的临界间隙和随车时距值如表1所示.
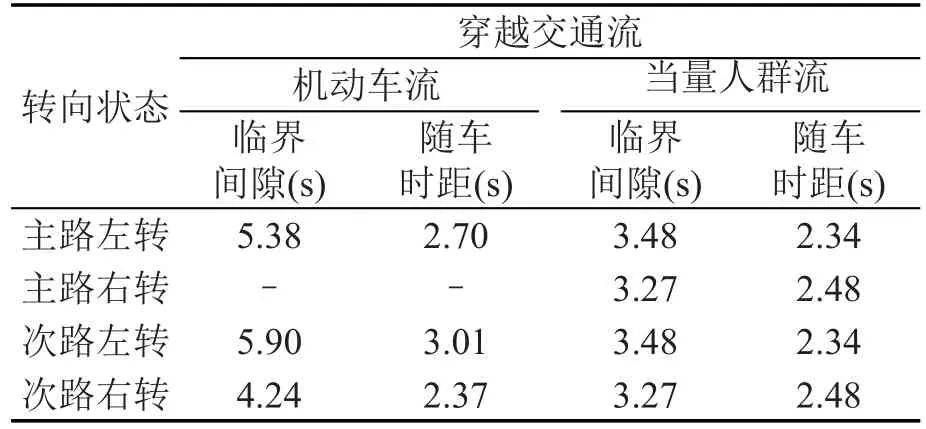
表1 临界间隙和随车时距值Table 1Critical gap and follow-up time values
按照图4所示的交通流标示方法,考虑主路共用车道情况,计算得到各次级交通流的可能通行能力和实际通行能力如表2所示.
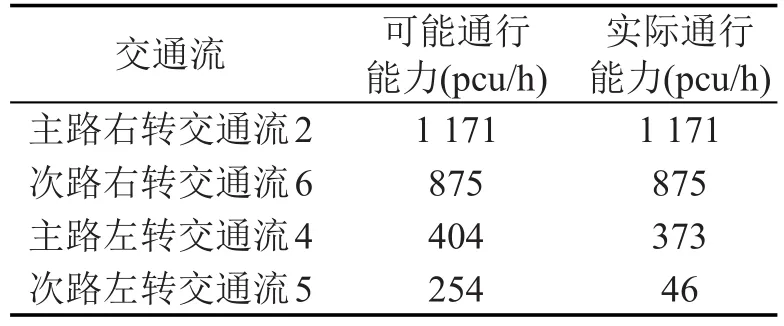
表2 次级交通流通行能力Table 2Capacity of minor streams
考虑次路共用车道情况,得到启蒙路入口的实际通行能力为153 pcu/h,该交叉口的实际通行能力为3 079 pcu/h.由上述计算可知,次路入口的交通需求已基本接近通行能力,经现场观察,该交叉口启蒙路入口交通已较为拥堵,计算结果和现场观测基本一致.
7 研究结论
以当量人群描述非机动车和行人对机动车通行的共同影响,对城市无信号控制T型交叉口的交通流运行等级进行了重新划分,共划分为五级.以主路直行车流和横穿支路的当量人群流作为独立优先流,采用间隙接受理论,得到各次级交通流的可能通行能力计算模型.考虑高等级次级交通流对低等级次级交通流的影响,采用概率论方法得到低等级次级交通流的可能通行能力修正系数.考虑当量人群的间隙分布,采用概率论方法得到横穿主路的当量人群流对次级交通流的可能通行能力影响修正系数.在上述分析的基础上,得到各次级交通流的实际通行能力计算模型,进而得到整个T型交叉口的通行能力计算方法.对于共用车道情况,参考HCM2000的研究成果,给出了该情况下交叉口通行能力的计算方法.实例分析表明,本文提出的计算方法符合我国城市无信号控制T型交叉口的交通流运行实际.
[1]钟剑华,吴晓层,简金宝.无信号T型交叉口次要道路通行能力分析[J].交通科技,2006(2):68-70.[ZHONG J H,WU X C,JIAN J B.Analysis traffic capacity at unsignalized T-intersections[J].Transportation Science &Technology,2006(2):68-70.]
[2]盛宇,吴中.基于Vissim仿真软件对无信号控制T型交叉口通行能力分析[J].交通与计算机,2005,23(1): 50-52.[SHENG Y,WU Z.Theoretical capacity of no signal T-type intersection based on Vissim[J].Computer and Communications,2005,23(1):50-52.]
[3]邹智军.计算机仿真法研究优先控制T型交叉口通行能力[J].中国公路学报,2000,13(3):101-105.[ZOU Z J.A study of capacity of major/minor priority T-intersection by means of computer simulation[J].China Journal of Highway and Transport,2000,13(3):101-105.]
[4]王炜,高海龙,李文权.公路交叉口通行能力分析方法[M].北京:科学出版社,2001.[WAGN W,GAO H L,LI W Q.Capacity analysis method on highway intersections[M].Beijing:Science Press,2001.]
[5]TRB.Highwaycapacitymanual(HCM)2000[R]. National Research Council,Washington,DC,2000.
[6]Finnish Road Administration.Capacity and level of serviceatfinnishunsignalizedintersections[R]. Helsinki,2004.
[7]陈吉发,李文权.混合流优先控制T型交叉口通行能力研究[J].交通科技与信息,2013,15(5):89-91,96. [CHEN J F,LI W Q.Research on the capacity of urban T-type priority intersection under mixed traffic flow[J]. Technology&Economy in Areas of Communications, 2013,15(5):89-90,96.]
[8]陈吉发.城市无信号控制T型交叉口通行能力研究[D].南京:东南大学,2007.[CHEN J F.Research oncapacityoftheurbanunsignalizedT-type intersection[D].Nanjing:Southeast University,2007.]
[9]Li A Z,Song X S,Song X H,et al.Traffic volume conditionforleft-turnforbiddenonurbanroad unsignalizedT-intersection[C].TheInternational Conference on Computational Intelligence and Software Engineering,2009.
[10]李爱增,王炜,李文权.城市道路交叉口当量人群运行特征[J].交通运输工程学报,2010,10(3):84-89.[LI A Z,WANG W,LI W Q.Running characteristics of equivalent people groups at urban road intersections[J]. Journal of Traffic and Transportation Engineering,2010, 10(3):84-89.]
[11]李爱增.城市道路交叉口空间布局及其通行能力研究[D].南京:东南大学,2008.[LI A Z.Research on lane distribution conditions and capacity of urban road intersections[D].Nanjing:Southeast University,2008.]
Capacity Calculation Method of Urban Road Unsignalized T-intersections
LIAi-zeng1,WANG Xiao-xiao1,LI Wen-quan2
(1.School of Transportation Engineering,Henan University of Urban Construction,Pingdingshan 467036,Henan,China; 2.School of Transportation,Southeast University,Nanjing 210096,China)
Taking the joint influence of non-motorized vehicles and pedestrians on motor vehicles into account,the priority of traffic flows is divided into 5 ranks.Let major-road through traffic flows and equivalent people groups crossing the minor road be independent priority streams,this paper studies the potential capacity of each minor stream by gap acceptance theory.Considering the effects of higher-rank minor-stream vehicles and equivalent people groups crossing the major road on lower-rank minor-stream vehicles,the paper studies the potential-capacity adjustment factors of each minor stream applying probability theory,and the movement capacity of each minor stream is obtained.So the capacity calculation method of urban road unsignalized T-intersections is acquired.The results indicate that analyzing the joint influence of non-motorized vehicles and pedestrians on motor vehicles by equivalent people groups can simplify the capacity calculation process,and the capacity calculation results is also accord with the running conditions of T-intersections with more non-motorized vehicles and pedestrians.
traffic engineering;urban road unsignalized T-intersection;capacity;gap acceptance theory; probability theory;equivalent people group;priority ranks
1009-6744(2015)05-0208-08
U491.4
A
2015-04-02
2015-09-05录用日期:2015-09-11
国家高技术研究发展计划(863计划)(2007AA11Z210);国家自然科学基金项目(50978057).
李爱增(1972-),男,河南汝州人,副教授,博士. *
liaizeng@163.com
