大型运动会专用道设置问题的多目标模型及其求解
2015-08-02李福清伍乃骐
李福清,伍乃骐
(广东工业大学 机电工程学院,广东 广州 510006)
大型运动会专用道设置问题的多目标模型及其求解
李福清,伍乃骐
(广东工业大学 机电工程学院,广东 广州 510006)
建立了大型运动会专用道设置问题的多目标模型。针对该多目标问题,划分目标的优先次序,将其降解为两个单目标模型。然后以一个简化的大型运动会交通网络进行仿真实验,实验结果表明,该模型更符合大型运动会的实际运输需求。
大型运动会;专用道设置问题;多目标模型;仿真实验
1 引言
在诸如亚运会、奥运会等大型运动会举办期间,组委会需要安排车辆接送运动员们往返于运动员村和比赛场馆之间。若前往比赛场馆或返回运动员村的行车时间太长,就不利于运动员们的赛前准备和赛后恢复。因此承办城市在申办时就会承诺这个行车时间必在可接受范围,如广州在申办2010亚运会时承诺这个行车时间不超过30min。在运动员村附近新建所有比赛场馆是不现实的,绝大多数情况是将现有体育场馆作为比赛场馆使用。而运动员村和一些场馆离得较远,车辆若按正常行驶的话,很难保证在规定时间内抵达。若在现有交通网络上设置专用车道,仅供运送运动员车辆行驶,由于该专用道上车辆少,也没有社会车辆干扰,就可以极大提高行车速度、减少行车时间,使运动员村与各比赛场馆之间的行车时间控制在规定时限内。事实上,北京奥运会、广州亚运会等大型运动会举办期间都采用了设置专用道的方法。但设置专用道这种交通管制措施,是以剥夺普通车辆对该车道的使用权为代价的,如果盲目设置必然招致受影响者的极大反对。因此在完成运送任务的前提下如何使专用道的设置代价最小是值得研究的问题。
吴瀛峰等人基于2010广州亚运会的实际应用背景,首次提出了基于大型运动会交通网络的专用道设置问题(Lane Reservation Problem in Transportation Network of Large Sports,LRPTNLS)的定义,并展开了相关的研究[1-4]。吴瀛峰等人所做的工作非常有意义,开拓了一个新的研究方向,并为后来者研究该问题奠定了基础,但仍存在着一些不足。本文分析了大型运动会中运送任务的特点和要求,在最小化专用道设置代价这个目标的基础上,提出增加最少化运送车辆数目的目标,据此建立相应的数学规划模型,并设计了两阶段算法进行求解,然后以一个简化的大型运动会交通网络的专用道设置作为实例来验证了模型和算法的正确性和有效性。
2 问题描述
2.1 专用道设置问题中交通网络的构成
一般使用网络图表示交通网络,其中节点分为源节点和终点节点,分别表示出发地和目的地,边或弧就表示路段,边或弧上的权表示该路段的参数,典型的如最短路径问题、车辆路径问题等。但在专用道设置问题中,网络图的含义有所不同。①在专用道设置问题中,每个路段需描述多个属性,这些属性至少包括:设置专用道后车辆通过该路段所需时间t1、未设置专用道车辆通过该路段所需时间t0及在该路段设置专用道的代价μ。因此网络图中边或弧的权是由多个属性构成的一个数组。②节点类型不仅包括源节点和终点节点,还包括中间节点,其表示从出发地到目的地途径的交叉路口。在路段上因某一运输任务的要求而设置专用道,则会产生专用道设置代价,而一旦设置后,其他运输任务的车辆通过该路段时均可使用该路段的专用道。专用道可重复使用但专用道设置代价仅需在第一次设置时计算1次。由于表示专用道设置代价的路段属性不具有累加性,在描述从源点到终点的交通路径时就不能省略途径的中间节点。若所有中间节点都考虑的话,则实际交通网络用网络图表示就会极其复杂。若某些连续路段仅被一个运输任务的车辆所使用,且假设这种连续路段仅考虑连在一起设或不设专用道,则可将这种连续路段视为一个路段,由此简化交通网络的表示。
据此,可用如图1所示的网络图表示大型运动会的交通网络。其中(如V0)表示源点即运动员村,⊚(如g1,…,g11)表示终点即各比赛场馆,○(如n1,…,n11)表示中间节点,并假设各路段来往双向的道路属性是相同的而使用双向箭头线来表示路段。
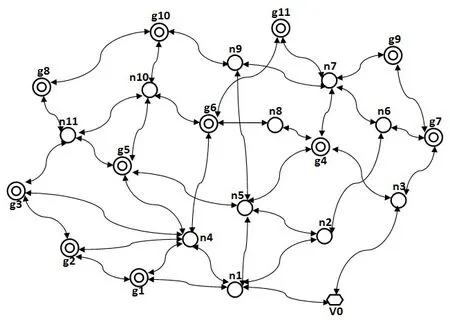
图1 大型运动会交通网络的网络图表示
2.2 求解目标
专用道规定只供执行任务的车辆使用,那么社会其他车辆要通过该交通网络时就会受到影响。若这种影响太大,他们可能就会反对设置专用道。因此,使整个交通网络上设置专用道的代价最小化是求解的第一目标。从运动员村到某一比赛场馆构成了一个运输任务,若有n个比赛场馆,则构成了n个运输任务。一辆车只执行其中一个任务。实际上,组织方会考虑将相邻场馆的运输任务合并为一个任务。一方面当参赛人数不是很多时可用一辆车运送从而减少车辆的使用,另一方面,减少任务数量可以减少其他管理成本。针对任务合并的要求,有两种解决方案。一种是在事前进行评估,将可在同一线路上的所有目标节点指定为任务的目标节点集合,如广州亚运会时前往大学城体育中心的任务还包含了各大学体育场馆这些节点集合,前往大夫山公园的任务还包含了英东体育馆节点[5]。这种方案需要决策者能准确了解线路管理和车辆使用等方面的成本。实际上这有一定的难度,所以可采取另一种更加可行的方案,即将最少化车辆使用数量作为第二求解目标。事实上,LRPTNLS还有其他的求解目标,但最小化专用道设置代价和最少化车辆使用数目是其中最主要的两个目标。
2.3 改进后的LRPTNLS定义
根据上面的分析,将LPRTNLS定义为:在大型运动会交通网 络 G=(V ,A) 中 ,V={0 ,1,2,…,n} 是 节 点 的 集 合 ,A={( i,j)|i,j∈V}是路段的集合,特殊节点0是作为起点的运动员村,S={1 ,2,…,n} 是除运动员村之外的节点,G={gi|i=1,2,…,m,m≤n,gi∈S}(即G⊆S)是作为目标节点的比赛场馆集合,O=S-G是既不是起点又不是终点的节点(即中间节点)的集合,每个路段 (i,j)具有权参数数组ωij=,,μij),∀(i ,j)∈A,其中t0ij是未设置专用道之前车辆通过路段(i,j)所需时间,是设置专用道后车辆从专用车道通过路段(i,j)所需时间,<t0ij,μij是在路段(i ,j)上设置专用道的代价,K={1 ,2,…,k},k≤m是执行运输任务的车辆集合,每辆车的容量无限制,车辆从起点到各目标节点的行驶时间不得超过规定时限ψ(为一常值)。问题的求解目标是在整个交通网络上使设置专用道的总代价最小,同时使用的车辆数最少。
3 建立问题的数学规划模型
在建立模型时,还需使用到的变量的含义见表1。

表1 变量符号含义
LRPTNLS问题的多目标线性整数规划模型如下:
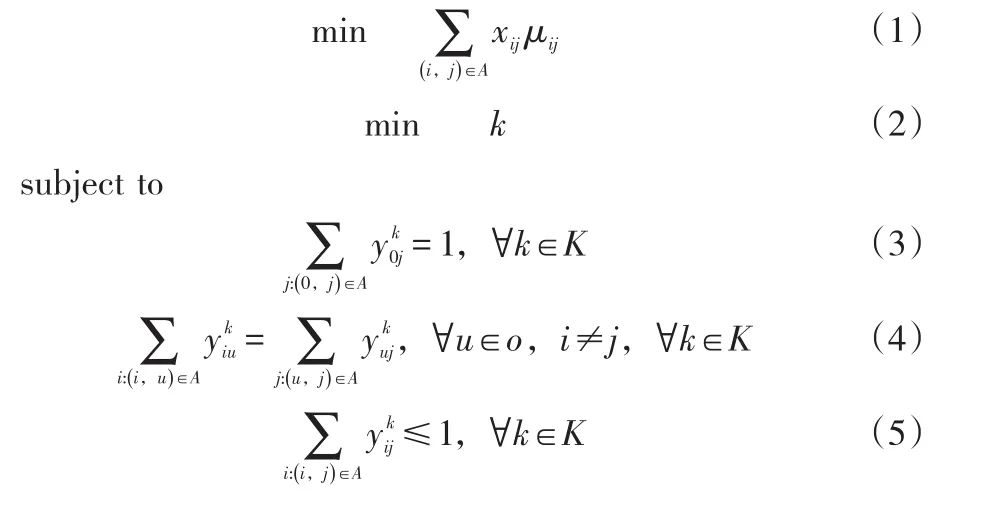
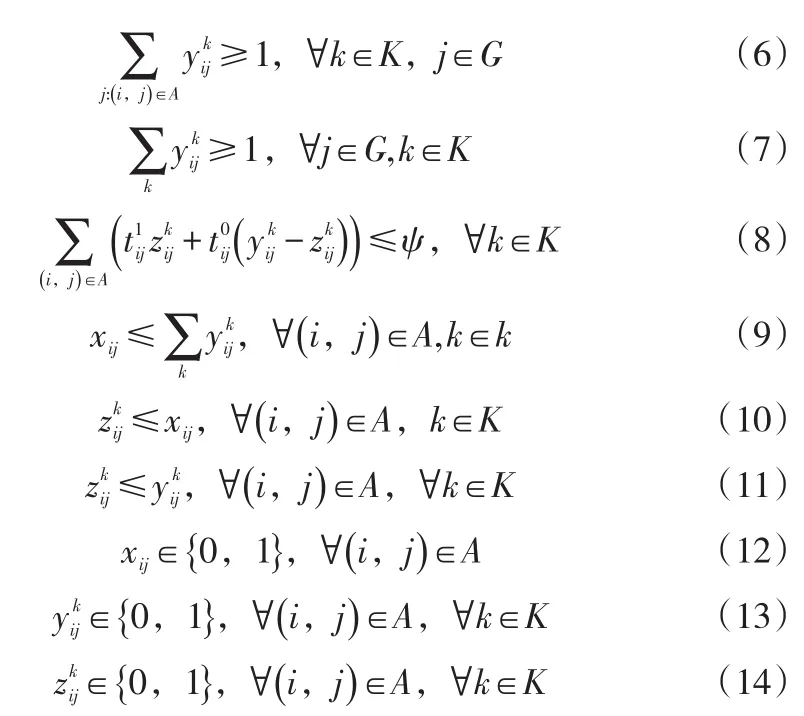
在上述模型中,目标函数由两部分构成,第一目标(1)是要求在交通网络上设置专用道的代价最小化,第二目标(2)是要求执行运输任务的车辆数量最少;约束条件(3)规定每辆车必须从起点0出发;约束条件(4)规定每辆车进入某个中间节点u后,必须从该节点u继续前进;约束条件(5)规定每辆车经过某节点i最多只能一次,避免车辆行驶路径包含回路;约束条件(6)规定每辆车至少为一个比赛场馆提供服务;约束条件(3)-(6)规定了每辆车必定从起点出发,途经中间节点最终抵达目标节点,且路径不包含环路;约束条件(7)规定每个场馆至少由一辆车提供服务;约束条件(8)规定了每辆车途径各个路段的通行时间总和不能超过规定的时限ψ;约束条件(9)规定至少有一辆车经过路段(i,j)才能在该路段设置专用道;约束条件(10)规定在路段(i,j)上最多只设置1次专用道;约束条件(11)规定了每辆车只有经过路段(i,j)时才能在该路段上设置专用道;约束条件(12)、(13)和(14)规定了变量取值范围为0或1。
4 分阶段求解与仿真实验
在大型运动会专用道设置问题上,最小化专用道设置代价这一目标是最重要和关键的,在此基础上,追求最少化运送车辆数目。因此,求解时,可将此多目标数学规划问题分成两阶段的单目标规划问题进行求解。
4.1 最小化专用道设置代价目标的模型
此时,每个场馆由一辆车来提供服务,因此公式(2)转化为一个约束条件:

同时,公式(6)也相应更改为:
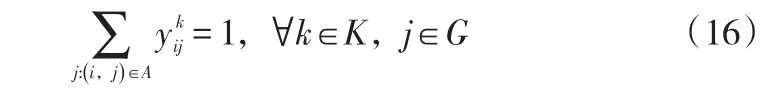
由公式(1)构成目标函数,约束条件(3)-(5),(7)-(16)构成该单目标的数学规划模型。
4.2 最少化运送车辆数目目标的模型
在前一步完成的基础上,建立目标是最少化运送车辆数目模型,然后进行求解。
完成最小化专用道设置代价目标求解后,不能再增设或更改专用道设置,此时交通网络各路段只用一个属性即行车时间 tij来描述(未设置专用道路段取,设置了专用道的路段取),约束条件仍是从起点到比赛场馆的总行车时间不得超过ψ,其公式为:

因此,由目标函数公式(2)、约束条件公式(3)-(7)、(13)和(17)就构成了第二阶段的数学规划模型。
4.3 仿真实验与分析
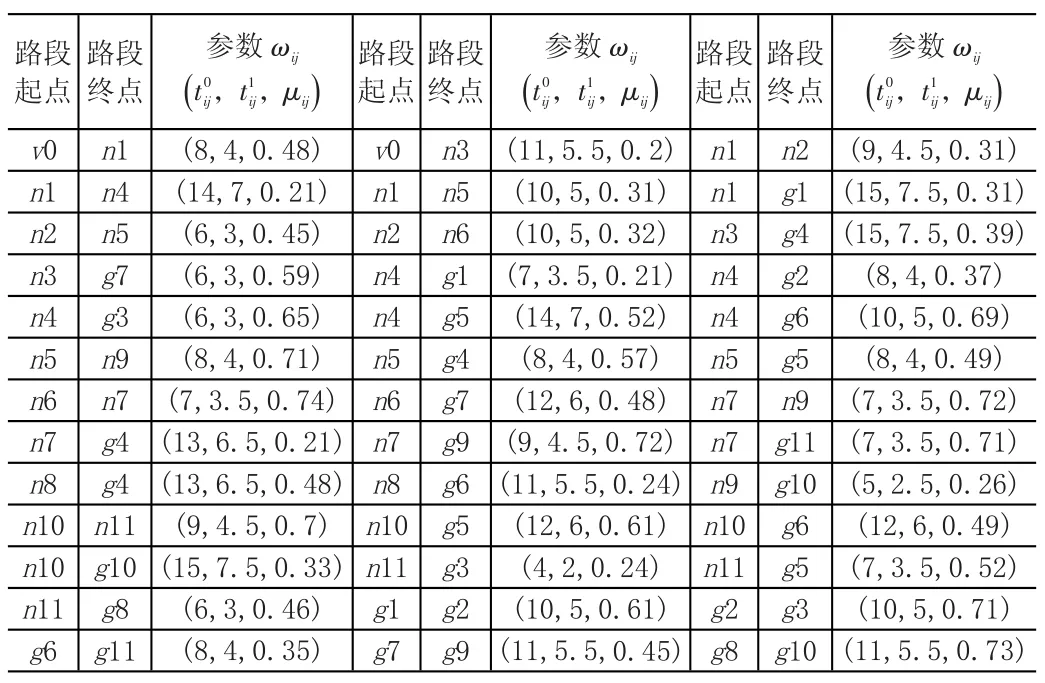
表2 大型运动会交通网络及路段参数
假设ψ=20,通过数学规划软件Lingo进行求解,结果表明只需在(v0,n1)、(v0,n3)、(n1,n4)、(n1,n5)、(n4,g6)、(n4, g3)、(n5,n9)、(g3,n11)、(n11,g8)、(g7,g9)、(g6,g11)这几个路段上设置专用道即可,得到整个交通网络专用道设置最小代价为4.77,11个场馆只需派出8辆车即可满足要求,车辆行驶路径见表3。

表3 车辆行驶路径与服务场馆
从实验结果可以看出,该模型解决了举办大型运动会在设置专用道时既要使得整个交通网络的专用道设置代价最小,又只安排最少数量的服务车辆的实际问题。
5 结语
大型运动会交通网络的专用道设置问题源于运输实际需求的一类重要的交通规划问题,自吴瀛峰等人提出该问题后,后来研究者的注意力主要集中于研究和设计该问题的优化算法,对产生问题的实际需求背景和问题本身少有人进行探讨。本文从举办大型运动会时的实际运输需求出发,提出了既需要使得整个交通网络专用道设置代价最小,还应该使用最少的运输车辆提供运输服务。据此,建立了大型运动会专用道设置问题的多目标模型,并以一个简化的大型运动会交通网络作为例子,通过数学规划软件进行求解,验证了本文的模型能够满足实际的需求,是正确有效的。
[1]吴瀛峰,伍乃骐,朱战国.大型运动会专用道设置的交通规划模型[J].工业工程,2009,12(6):96-100.
[2]吴瀛峰,伍乃骐,朱战国.求解基于专用道设置的动态交通规划问题的启发式算法[J].运筹与管理,2009,18(5):38-42.
[3]吴瀛峰.基于专用道设置的交通规划问题的建模与求解[D].广州:广东工业大学,2010.
[4]Wu Y F,Chu C B,Chu F,et al.Heuristic for lane reservation problem in time constrained transportation[A].Proceedings of the Fifth Annual IEEE International Conference on Automation Science and Engineering[C].Bangalore,India,2009.
[5]李福清,伍乃骐.运送任务合并下专用道设置问题的建模与求解[J].系统工程理论与实践,2014,(6):1 599-1 606.
[6]李湘勇.车辆路径问题模型及算法研究[D].上海:上海交通大学,2007.
[7]Zhou Z,Chu F,Che A,et al.A multi-objective model for the hazardous material transportation problem based on lane reservation[A].In:Proceedings of IEEE International Conference on Networking,Sensing and Control[C].2012.
[8]Yunfei Fang,Feng Chu,Said Mammar,et al.Iterative Algorithm for Lane Reservation Problem on Transportation Network[A].In:2011 InternationalConference on Networking,Sensing and Control[C].Delft,the Nethelands,2011.
[9]B W Waxman.Routing of multipoint connections[J].IEEE Journal on Selected Areas in Communications,1998,6(9):1 617-1 622.
[10]Fang Y,Chu F,Mammar S,Zhou M.Optimal Lane Reservation in Transportation Network[J].IntelligentTransportation Systems,IEEE Transactions on Intelligent Transportation Systems,2012,13(2):482-491.
[11]郝光,张殿业,冯勋省.多目标最短路径模型及算法[J].西南交通大学学报,2007,(5).
[12]张孜,林晓丽.广州亚运会车辆调度信息系统设计与实践[J].交通运输系统工程与信息,2011,(5).
[13]王书灵,陈金川,郭继孚,李春艳.交通需求管理政策在北京奥运会中的应用和评价[J].交通运输系统工程与信息,2008,(6).
[14]齐建宇.快速路公交专用道设置条件研究[J].交通建设与管理,2015, (10).
[15]王继强.基于LINGO的旅行商问题的建模方法[J].计算机工程与科学,2014,(5).
[16]张晓倩.应急救援中多目标车辆路径问题研究[J].交通科技与经济, 2015,(1).
Establishment and Solution of Multi-objective Model for Dedicated Lane Setup during Large-scale Sports Meetings
Li Fuqing,Wu Naiqi
(School of Electrical&Mechanical Engineering,Guangdong Institute of Technology,Guangzhou 510006,China)
In this paper,in view of the multi-objective problem in the setup of the dedicated lanes during large-scale sports meetings, we first ranked the priority of the objectives to reduce the multi-objective model into two single-objective models,then through a simulation experiment on the simplified traffic network of a large-scale sports meeting,demonstrated that the model was capable of satisfying the practical transportation demand of the sports meeting.
large-scale sports meeting;dedicated lane setup problem;multi-objective model;simulation experiment
TU245;F224
A
1005-152X(2015)10-0146-03
2015-08-12
李福清(1976-),男,江西玉山人,讲师,博士研究生,研究方向:智能交通与物流、组合优化模型与算法;伍乃骐(1949-),男,教授,博士生导师,国务院特殊津贴专家,研究方向:制造系统及设计、智能交通系统、生产计划与调度和控制、离散事件系统及Petri网理论、信息安全和计算机网络入侵检测。
10.3969/j.issn.1005-152X.2015.10.040
