基于SVM的生鲜食品货架期预测

袁彦彦，王兴芬

（北京信息科技大学 信息管理学院，北京 100192）

基于SVM的生鲜食品货架期预测

袁彦彦，王兴芬

（北京信息科技大学 信息管理学院，北京 100192）

采用支持向量机（SVM）的方法对零售商生鲜食品的货架期预测问题进行了研究，建立了货架期预测模型，以速冻水饺为例，在Matlab环境下对该模型进行了仿真实验，并与BP神经网络模型的预测值比较，结果表明该模型预测得到的货架期与实际值有更好的拟合度，提高了预测的准确性，为生鲜食品的货架期预测提供了新途径。

支持向量机；生鲜食品；货架期；预测

1 引言

随着生活水平的提高，人们无论是对食品的品质还是安全性，都提出了更高的要求。其中生鲜食品属于温度敏感货物，不可避免地存在着腐败变质的风险。货架期是指货物能满足顾客对食品质量要求的时间期限，当食品自身的某种特性达到不可接受时，即为该货物的货架期终点[1]。近年来，针对生鲜食品货架期的研究成为食品安全领域的热点之一，且多以易腐食品为研究对象，在低温范围内或波动温度条件下进行实验，试图通过可观测的食品变化的特征指标，来反映食品的品质变化，从而确定生鲜食品的货架期，但由于低温导致食品衰败的机制比较复杂，构建模型所采用的方法大多数都有一定的适用范围和对象。而本文采用的SVM方法适用范围广、稳定性高，用于解决生鲜食品构建货架期预测模型的问题，不仅能为生鲜货架期预测提供新途径，也可以为生鲜食品的销售管理提供参考依据。

2 货架期预测模型研究分析

在生鲜食品的腐败过程中，始终伴随着各种物理化学反应和体内微生物的活动，间接或直接地影响着生鲜食品的货架期，影响生鲜食品货架期的因素主要可分为感官指标、理化指标和微生物指标，其中感官指标又包括颜色、风味、形态、质地、持水力等；理化指标包括温度、水分含量、PH、酶、TVBN、叶绿素等；微生物指标包括特种菌含量、菌落总数等。根据这些指标，当前生鲜食品的货架期预测模型的构建方法主要有微生物学法、Arrhenius法、神经网络方法、威布尔危害分析法以及Q10模型[2-17]，方法及其特点见表1。

通过上述分析以及文献的调研，从指标来看，以往研究多以某种特定指标比如特种菌、挥发性盐基氮，作为建立货架期的衡量指标，实验中食品品质指标间关联度以及品质指标与货架期之间的关系研究不足，影响了预测结果的准确性[2-8]；从货架期模型的构建方法来看，主要是基于特定的研究对象，选用适合的方法构建货架期模型，这样的模型存在针对性和适用范围的限制性[2-17]，并且在所使用的Arrhenius方法中，因货架期是伴随着化学反应发生的，与温度有关，大多数研究者通过实验获取该方法中公式的参数并设定为常数，但实际上参数是与温度存在关系的，间接地影响结果的准确性[18]。而支持向量机方法已经在其他领域得到了较广的应用[19-22]，且在货架期预测模型的研究中采用该方法的研究尚少，本文则采用该方法对生鲜食品货架期进行研究，构建生鲜食品的货架期预测模型。

表1 货架期模型构建方法

3 基于支持向量机的预测模型分析

在统计学理论和数学基础上发展起来的支持向量机（Support Vector Machines，SVM）是一种新的机器学习方法，适用范围广，稳定性高，具有较好的“鲁棒”性，已非常成功地处理回归和模式识别等诸多问题，其中支持向量机回归算法（Support Vector Machines Regression，SVMR）可以解决线性或非线性回归问题，进行时间序列预测或非线性建模与预测。本文采用支持向量机的回归算法进行预测，其基本思想是通过非线性变换ϕ，将输入空间变换到一个高维数的特征空间，并在这个空间中进行线性回归，这样在高纬特征空间的线性回归就对应于低维输入空间的非线性回归。主要的操作是通过定义适当的核函数K(x,y)=ϕ(x)∙ϕ(y)来实现这个非线性变换。在实际应用中，常用的核函数包括线性核函数、径向基核函数、多项式内积核函数。

根据SVM回归理论建立生鲜食品货架期预测模型，如图1所示。

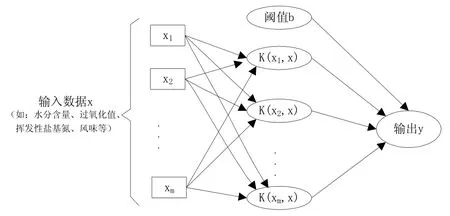
图1 货架期预测的SVM模型

在预测模型的建立过程中，设生鲜食品货架期预测的指标数据样本集为{(yi,xi),i=1,2,...,n}，其中x∈Rn,y∈Rn，xi是模型的输入数据，表示与生鲜食品腐败高相关的因变量指标，比如风味、总体接受性、水分含量、过氧化值、酸价、菌落数等；yi是预测模型的输出数据，表示作为衡量货架期的结果指标，比如有效积温、挥发性盐基氮、微生物含量等。那么回归预测模型用下列方程表示：

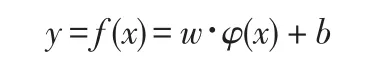
式中，w为权向量，φ(x)为非线性映射函数，b为阈值。

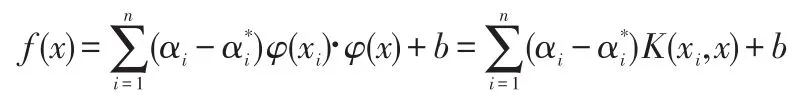
式中 αi、为拉格朗日因子。根据生鲜食品的指标值，由上式即可以对生鲜食品的货架期进行预测。

4 仿真实验

本文仿真实验数据来源于文献[9]，其中数据是该文献作者在-28～-12℃温度波动下进行实验以及感官评价获得的，并且还设定了将贮藏有效积温40 332h·℃作为速冻水饺货架期终点，具体数据见表2。在文献[9]中利用BP神经网络建立生鲜食品速冻水饺的货架期预测模型，通过预测水饺的有效积温计算得到水饺距货架期终点的时间，即剩余货架期。在Matlab环境下，对建立的基于SVM的预测模型进行实验，并与参考文献的实验结果进行比较，最后为验证本文所用方法的有效性，又进行了组合指标的预测。

对应图1所示模型，输入数据x即为风味、总体接受性、水分含量、亨特白度、酸价和过氧化值，输出数据y即为有效积温。本次实验中在Matlab的环境下进行生鲜食品货架期的SVM预测模型的仿真实验。其步骤为：

（1）按照格式要求准备数据集。同文献[9]一致，选取表中16组作为训练数据，其余5组（9、12、13、16、17）数据作为测试数据。输出为有效积温（y），其余为输入变量。

（2）将模型训练数据和测试数据都进行归一化处理；然后采用交叉验证对主要参数c与g（惩罚参数c和核函数参数g）进行寻优，精细化寻优后c和g的范围为2-4到24，步长为3，通过参数迭代，寻找出使得模型训练误差值最小的c、g参数组合，结果如图2所示，c值为16，g值为0.203 06，此时交叉验证的均方误差（MSE）为0.000 387 62。

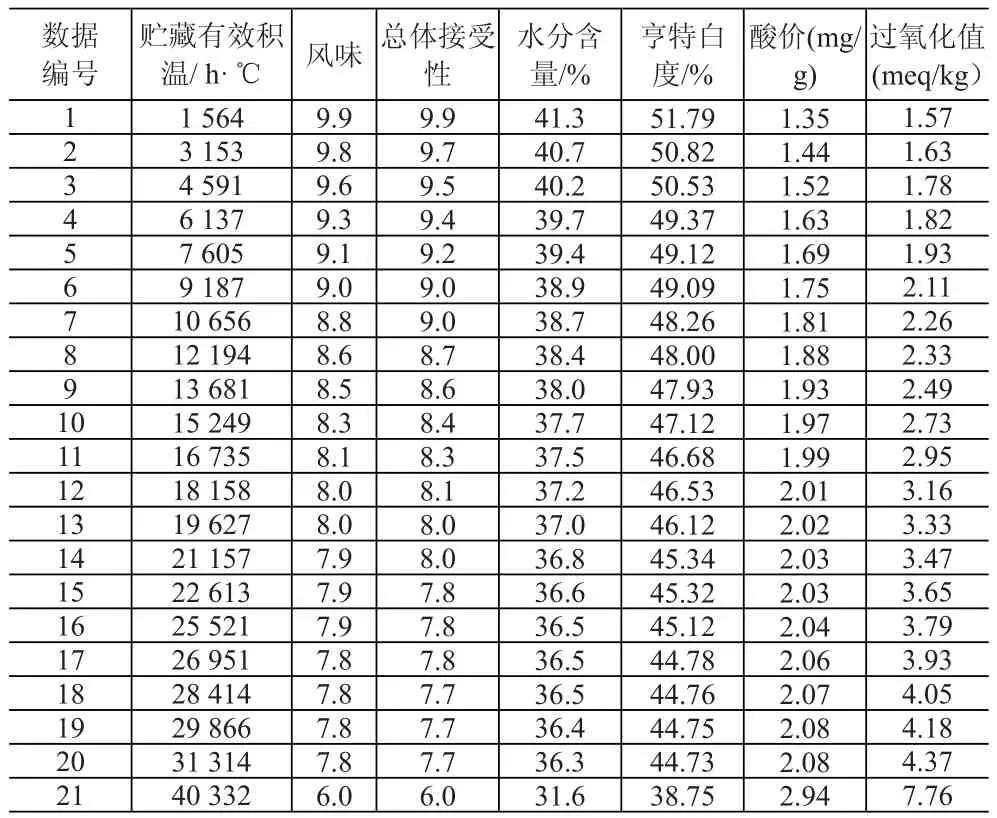
表2 各测试指标数值

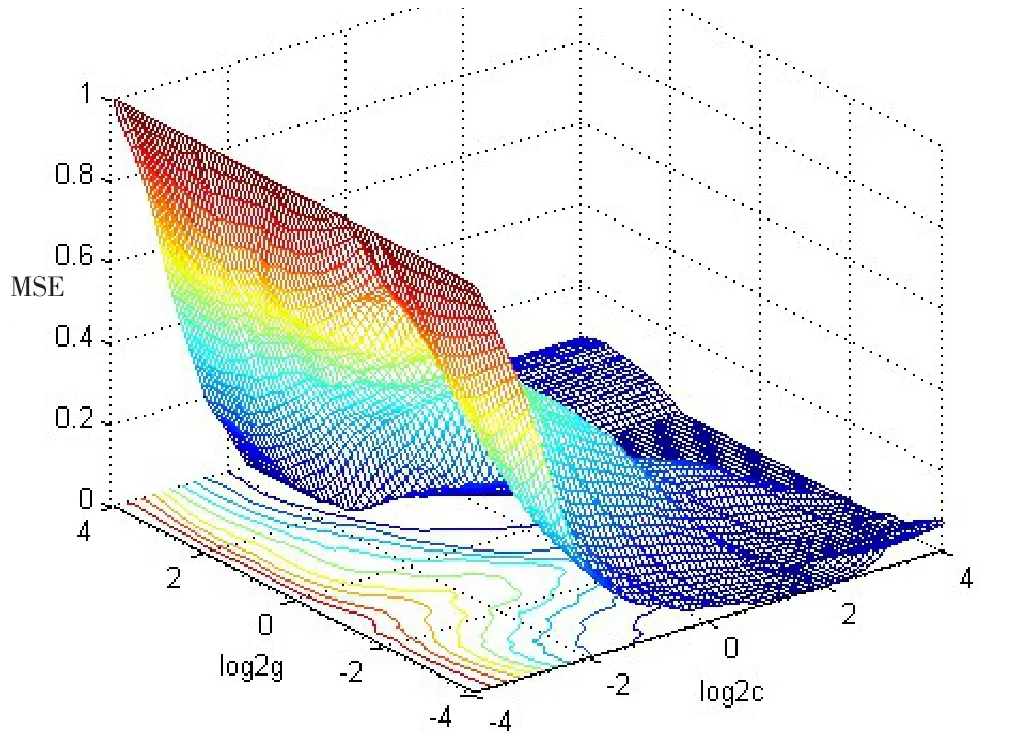
图2SVM参数优化3D视图

（3）利用上面得到的最佳参数对SVM进行训练，建立预测模型model，为判断模型的有效性，首先对训练数据进行了回归预测，得到的预测效果较好，然后对测试数据集进行测试和预测，预测结果如图3所示，相关系数为0.991 3，MSE为0.01%。

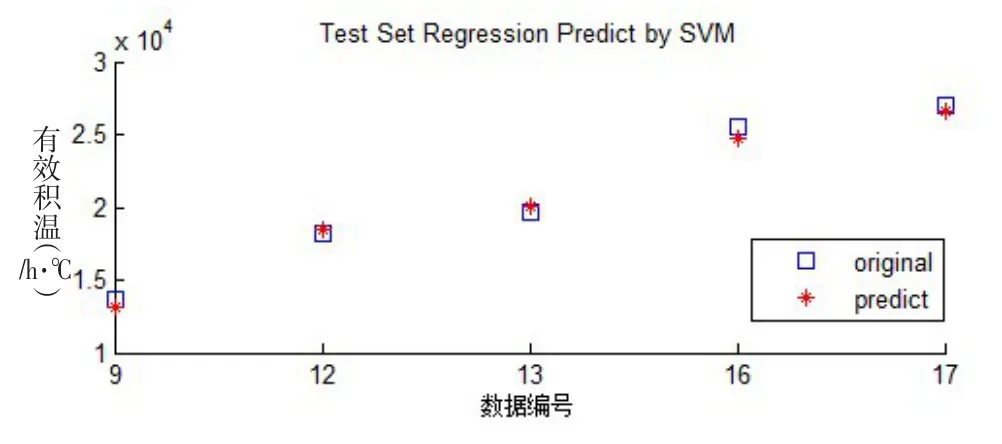
图3 测试样本模型预测结果

根据上述预测结果，将参考文献中所用的BP神经网络预测模型与本文采用的SVM预测模型以及实际测定值相比较，见表3，其中距货架期终点积温=终点积温-有效积温预测值，并计算距货架期终点积温的相对误差。

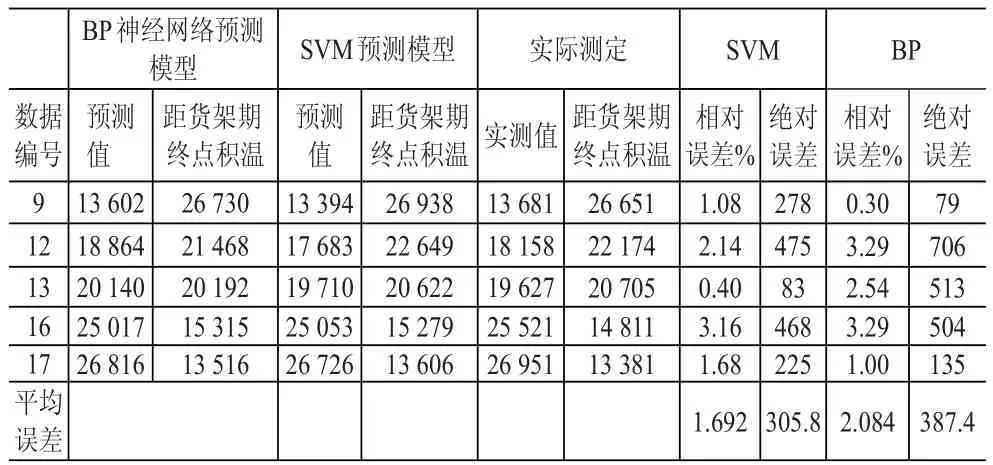
表3 有效积温预测值及验证

从表3可以我们看出，平均相对误差SVM模型要比BP神经网络模型小0.392，且平均绝对误差也相应的小81.6。再对这两种方法再进行误差评估，计算两种预测模型的有效积温预测值与实际值的误差均方差，得到BP神经网络的误差均方差为497.5，而SVM的误差均方差为228.1，明显要小于前者。所以基于统计理论和数学为基础的支持向量机回归模型，要比BP神经网络的预测效果更理想。根据文献[9]中有效积温的计算公式（其中K为有效积温h·℃，T为实测的冷藏温度℃，C是相对零点，N是冷藏时间），假定测试样本数据是在恒定温度-15℃下测定，对SVM模型预测结果和文献[9]BP神经网络模型所预测结果分别计算货架期，并进行比较，见表4。

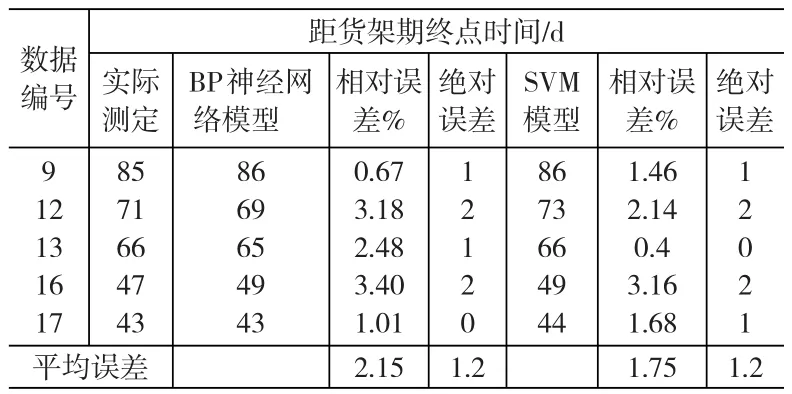
表4 BP神经网络与SVM货架期预测结果比较

从预测值来看，两种预测模型所得结果的平均相对误差中，SVM要比BP小0.4，虽然两者的绝对误差相等，但对其再进行误差评估，得到BP神经网络模型的误差均方差（1.58）要大于SVM的误差均方误差（0.836）。

上面所述是将有效积温作为货架期的终结指标，而过氧化值也是一种检测食品质量和变质程度的指标，产品的卫生标准规定，过氧化值不得大于0.2%，即15.76meq/kg，则利用SVM模型对有效积温和过氧化值进行组合预测，不但可以对货架期进行预测，还可以起到一定程度的预警作用。重新随机选取训练及测试数据进行实验。在进行实验之前，利用SPSS软件对预测指标进行简单相关性分析，两者相关性系数r=0.94，p＜0.01显著相关，再对其进行偏相关分析，即在控制其他变量的情况下，分析有效积温和过氧化值之间的相关性，结果见表5。

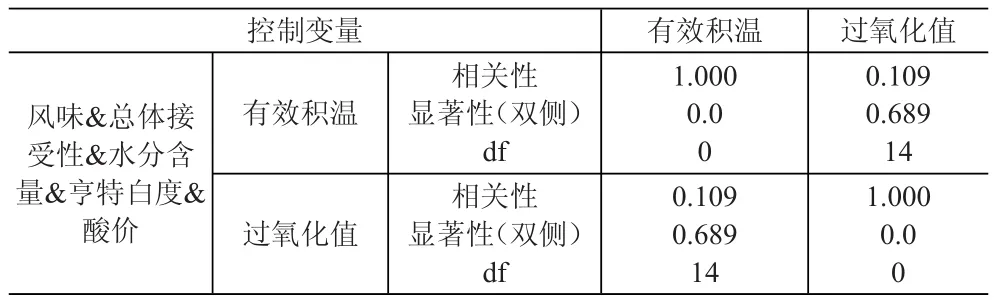
表5 相关性分析结果

结果表明，两者相关系数r=0.109＜0.3，存在弱相关，且p= 0.689＞0.05，两者之间不存在显著的相关关系，最后对有效积温和过氧化值进行基于SVM模型的组合预测，结果见表6。

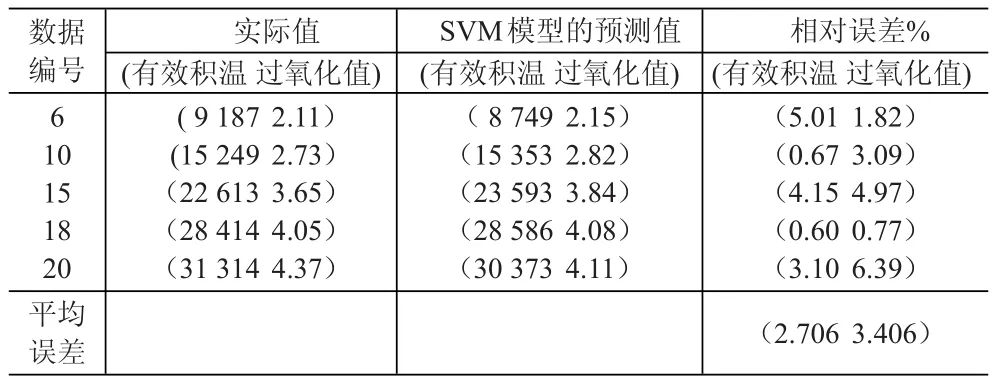
表6 SVM模型对有效积温和过氧化值的组合预测结果及验证

从表6可知，SVM模型的预测结果中有效积温的最大相对误差为5.01%，平均相对误差为2.706%，过氧化值的最大相对误差为6.39%，平均相对误差为3.406%，说明此模型可有效地进行组合预测货架期，也说明了预测模型的实用性和有效性。

5 结论

SVM使用范围广，可以较好地解决小样本、非线性、高维数、局部极小值等实际问题且具有良好的推广价值，本文采用该方法对生鲜食品货架期预测进行了研究，建立了模型，且以参考文献[9]中的速冻水饺为例，利用Matlab对该模型进行仿真实验，并将结果与参考文献[9]所用的BP神经网络预测模型的预测结果进行了比较，结果显示本文SVM模型的预测值与实际值的相对误差最大为3.1%，比BP神经网络模型的预测结果更能接近实际情况，更为理想。最后又通过将速冻水饺的指标组合预测，再次说明了SVM模型的可用性和有效性，以及可以更好地为生鲜食品货架期管理提供有效的参考依据，并为生鲜食品的货架期预测提供新途径。

[1]胡位歆,金王平,刘东红.冷链食品品质（货架寿命）预测模型的建立方法[J].中国食物与营养,2014,20(5)：45-49.

[2]宋晨,刘宝林,王欣,等.冷冻羊肉剩余货架期预测模型研究[J].食品科学,2010,31(6):279-282.

[3]Alejandra Tomaca,Rodolfo Horacio Mascheronib,María Isabel Yeannes.Modelling the effect of gamma irradiation on the inactivation and growth kinetics of psychrotrophic bacteria in squid rings during refrigerated storage.Shelf-life predictions[J].Journal of Food Engineering,2013,117(2):211-216.

[4]Stefanie Bruckner,Antonia Albrecht,Brigitte Petersen.A predictive shelf life model as a tool for the improvement of quality management in pork and poultry chains[J].Food control,2013,29(2):451-460.

[5]佟懿,谢晶.鲜带鱼不同贮藏温度的货架期预测模型[J].农业工程学报,2009,25(6):301-305.

[6]范新光.鲜切西兰花减压冷藏保鲜技术与货架期预测模型的研究[D].烟台:烟台大学,2014.

[7]李汴生,黄智君,张晓银,等.冷配送莴笋菜肴的货架期预测模型建立与评价[J].现代食品科技,2015,31(3):177-183.

[8]谢晶,张利平,高志立,等.鸡毛菜的品质动力学分析及货架期预测模型[J].食品科学,2014,35(10):268-272.

[9]潘治利,张卓,黄忠民,等.BP神经网络结合有效积温预测速冻水饺变温冷藏货架期[J].农业工程学报，2012,28(22):276-281.

[10]Sumit Goyal,Gyanendra Kumar Goyal.Cascade Artificial Neural Network Models for Predicting Shelf Life of Processed Cheese[J].Journal of Advances in Information Technology,2013,4(2):80-83.

[11]Ubonrat Siripatrawan,Pantipa Jantawat.A novel method for shelf life prediction of a packaged moisture sensitive snack using multilayer perceptron neural network[J].Expert Systems with Applications,2008, 34(2):1 562-1 567.

[12]蔡超.酸奶在贮存期间参数的变化和对货架寿命预测模型的研究[D].武汉:华中农业大学,2012.

[13]张丽平,余晓琴,童华荣.Weibull模型在板鸭货架寿命预测中的应用[J].食品科技,2010,35(2):111-113.

[13]W S Duyvesteyn，E Shimoni,T P Labuza.Determination of the End of Shelf-life for Milk using Weibull HazardMethod[J].LWT-Food Science and Technology,2001,34(3):143-148.

[14]顾海宁.冷却猪肉贮存中的品质变化及货架期预测[J].现代食品科技,2013,29(11):2 621-2 626.

[15]刘春芝,许洪高,李绍振,等.柑橘类果汁货架期研究进展[J].食品科学,2012,33(13):292-298.

[16]S Limbo L,Torri N,Sinelli L,Franzetti E.Casiraghi.Evaluation and predictive modeling of shelf life of minced beef stored in high-oxygen modified atmosphere packaging at different temperatures[J].Meat Science,2010,84(1):129-136.

[17]Wenli Dong,Xue Gong,Jing Dong etc.Oxidation kinetics of hazelnut shelf-life prediction model[J].Applied Mechanics and Materials, 2012,200:466-469.

[18]陈海建,滕克难,等.基于修正Arrhenius方法的SRM药柱储存寿命预估[J].弹簧与制导学报,2011,31(4):232-235.

[19]聂铭,周冀衡,等.基于MIV-SVM的烤烟评吸质量预测模型[J].中国烟草学报,2014,20(6):56-62.

[20]秦永宽,黄声享,赵卿.基于小波消噪和LS-SVM的混沌时间序列预测模型及其应用[J].大地测量与地球动力学,2008,28(6):96-99.

[21]刘俊娥,慕柠咛,刘丙午.固有模态SVM预测模型在零售销量预测中的应用[J].物流技术,2013,23(11):76-78.

[22]曹秋勤.基于支持向量机的蔬菜质量安全预测及溯源模型的研究与应用[D].广州:华南理工大学,2014.

Study on Fresh Food Shelf Life Forecasting Based on SVM

Yuan Yanyan,Wang Xingfen
(School of Information Management,Beijing University of Information Technology,Beijing 100192,China)

In this paper,we used the support vector machine to forecast the shelf life of the fresh food of a retailer,built the shelf life forecasting model,then in the case of the quick-frozen dumpling,conducted a simulation experiment of the model under the Matlab environment;next we compared the result yielded with that by the BP neural network model and demonstrated that the model established in this paper fitted more closely with the actual value and was thus more accurate.

SVM;fresh food;shelf life;forecasting

TS207；TP399

A

1005-152X(2015)10-0064-04

2015-07-01

北京市教委科技重点项目“电子商务平台交易纠纷规避的若干支撑技术研究”（KZ201411232036）

袁彦彦（1988-），女，山东临沂人，北京信息科技大学信息管理学院硕士研究生，研究方向：物流工程；王兴芬（1968-），女，教授，博士，研究方向：物流管理、电子商务与WEB安全。

10.3969/j.issn.1005-152X.2015.10.019