非齐次双曲型守恒律组的整体解的研究

丁美玲

(南京航空航天大学理学院数学系，南京210016)

非齐次双曲型守恒律组的整体解的研究

丁美玲

(南京航空航天大学理学院数学系，南京210016)

主要是在文献［1］的齐次方程的基础上对非齐次的双曲型守恒律的整体解进行研究，主要对两个问题进行了研究，第一个是如何除了非齐次项，主要是利用广义的Glimm把非齐次的转化为齐次的.第二个是证明解的存在性.主要利用激波的一些性质.

双曲守恒律;整体解;广义Glimm;激波

1 研究的始值问题

始值u0(x)，v0(x)适合:

(i)对任意的x1＜x2，x1x2＞0有

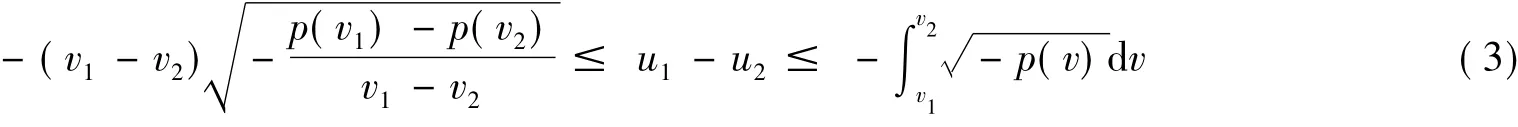
其中(ui，vi)=(u0(xi)，v0(xi))i=1，2.

(ii)在x=0时

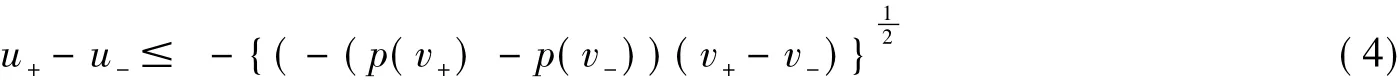
其中(u±，v±)=(u0(0±0)，v0(0±0)).

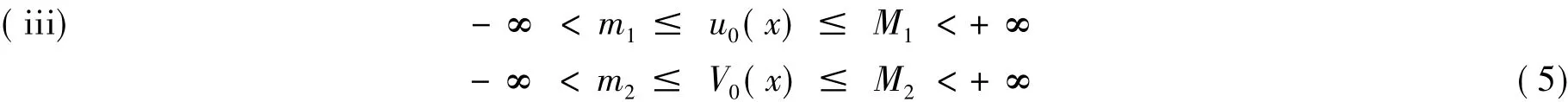
定义1在上半平面(t≥0，－∞ ＜x＜+∞)上定义的有界可测函数u(x，t)，v(x，t)为齐次方程的广义解，如果对任意的φi(x，t)∈(t≥0，i=1，2)有

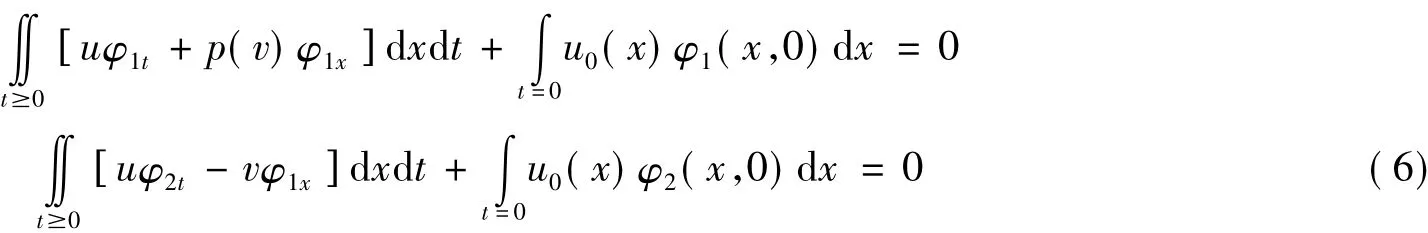
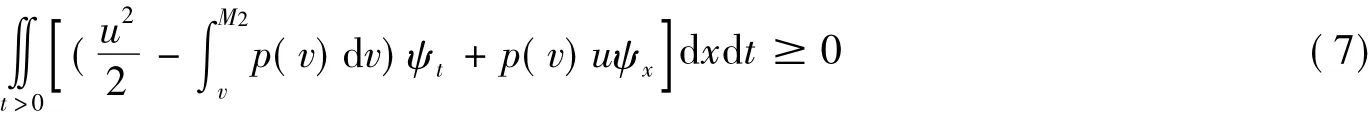
2 主要的思想和方法

(1)对于齐次方程，其激波和特征线为:

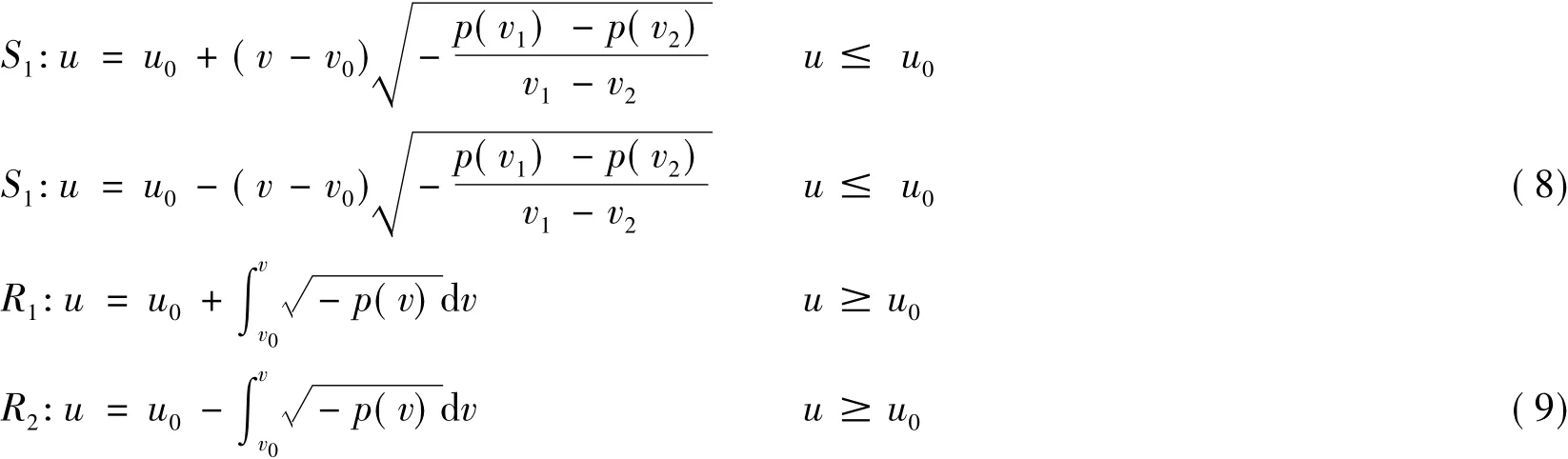
它们分别是能够同(u0，v0)用后向前向中心稀疏波或激波连接的所有右状态(u，v)的集合这四条向曲线把(u，v)平面分成四个角区域，分别记为Ⅰ(p0)，Ⅱ(p0)，Ⅲ(p0)，Ⅳ(p0)，(p0=(u0，v0)).

其具有如下的性质(具体可见参考文献［1］)

性质1若(u1，v1)∈S1(u0，v0)，则S1(u1，v1)∈Ⅲ(p0)，(u≤u1)

若(u1，v1)∈S2(u0，v0)，则S2(u1，v1)∈Ⅱ(p0)，(u≤u1)

性质2沿激波极线(逆激波极线)，r1和r2均严格单减(单增)且对其上任意两点A，B有，沿后向(前向)特征轨线，r1严格单增，r2不变(r2严格单增，r1不变).其中为齐次方程的黎曼不变量).

性质3从后向(前向)特征轨线或激波极线上任两点引出的前向(后向)激波极线不相交.

性质4从前向(后向)特征轨线上任两点引出的前向(后向)激波极线不相交.

性质5从前向(后向)激波极线上任一点引出后向(前向)激波极线两者仅有这一交点.

(2)用广义的Glimm格式在齐次方程的基础上把非齐次项加进去，具体方法如下:给变量x，t以步

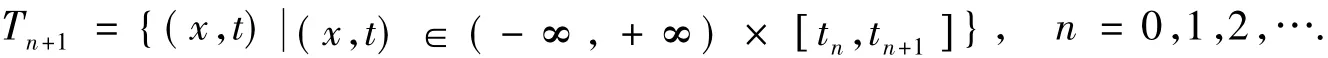
当h≤t＜2h，令Us(x，t)=Us((m+1+θ)，s－0)，m l＜x＜(m+2)l，m为奇数，则t=h上是分片常数，记作U1m+1(m为奇数)，再解黎曼问题其解为(x，t).令，则Us(x，t)=(vs(x，t)，us(x，t))T即为近似解.设t＜kh已定义，先定义t=kh，解黎曼问题，令

Uks(x，t)=Uks((m+1+θ)，s－0)，m l＜x＜(m+2)l，则t=kh是分片常数，记为(m为奇数)，再解黎曼问题其解为(x，t).令则 Us(x，t)=(vs(x，t)，us(x，t))T即为非齐次方程的近似解.

3 广义解的存在性

引理1若ur(x，t－)，vr(x，t－)是齐次方程的参考解，则参考解ur(x，t)，vr(x，t)在带域Tn+1内至多有一个前向激波，其他均为前向稀疏波和后向激波.

证明 若齐次方程在Tn+1层以ur(x，t－)，vr(x，t－)为参考解，由参考文献［1］可知引理正确，现把ur(x，t－)变为原来的(1－αs)倍，相当于将其向左平移，vr(x，t－)不变，由性质1－5可知，引理正确.

推论1［见1］r1(ur(x，t)，vr(x，t))对任何t是x的不增函数.

引理2［见1］ 与引理1相同假设下如参考解ur(x，t)，vr(x，t)在任何带域Tk(Tk:{ks＜t≤Ns，N＞k≥0}，N为正整数或+∞)都含有一个前向激波，其位置x=xr(t)，(0＜t≤Ns)，则

(i)ur(xr(t)－0，t)和vr(xr(t)+0，t)是t的不增函数.

(ii)vr(xr(t)+0，t)－vr(xr(t)－0，t)是t的不增函数，(0＜t≤Ns).

推论2［见1］ 在t＞0内vaxr vr(x，t)是t的不增函数.

引理3［见1］ 参考解ur(x，t)，vr(x，t)在t等于常数t＞0时，对x的总变差一致有界.

定理1 始值问题(1)，(2)式在始值适合条件(3)～(5)的式时，在上半平面(t≥0，－∞ ＜x＜+∞)存在着广义解(u(x，t)，v(x，t))它同ur(x，t)，vr(x，t)一样，满足u(x，t)，v(x，t)的变差有界，且在t＞0内(x，t)是t的不增函数，r1(u(x，t)，v(x，t))对任何固定的t是x的不增函数.

［1］ 丁夏哇，张同，王靖华，等.拟线性守恒律方程组的整体解［J］.中国科学，1973(3):239－254.

［2］ 张同，郭于法.一类拟线性方程的整体解［J］.数学学报，1965，15:386－396.

［3］ LAX PD.Hyperbolic systems of conservation lawsⅡ［J］.Comm.Pure.Appl.Math.，1957，10:537－566.

［4］ SMOLLER JA，JOHNSON JL.Global solutions for an extended class of hyperbolic systems of conservation laws［J］.Archive for Rational Mechanics and Analysis，1969，32(3):169－189.

［5］ SINESTRARIC.Large time behavior of solutions of balance law with periodic initial data［J］.Nonlinear Differential Equations Appl.，1995，2:111－113.

［责任编辑 王新奇］

On the G lobal Solution of Nonhomogeneous Hyperbolic System of Conservation Laws

DINGMei－ling

(Department of Mathematics，School of Science，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

Based on the nonhomogeneous formula in reference［1］，this study addresses the global solution of nonhomogeneous hyperbolic system of conservation laws.Two issues are discussed.The first is on the way of deleting nonhomogeneous term，The method suggested is to convert the nonhomogeneous into the homogeneous bymeans of generalized Glimm.The second is to prove the existence of solution by shock wave.

hyperbolic conservation law;global solution;generalized Glimm;shock wave

1008－5564(2015)01－0019－03

O715.27

A

2014－08－29

丁美玲(1989—)，女，安徽宿州人，南京航空航天大学理学院数学系硕士研究生，主要从事守恒律方程整体解研究.