酉系统上的多元K－框架向量

郑帅

(南京航空航天大学理学院数学系，南京210016)

酉系统上的多元K－框架向量

郑帅

(南京航空航天大学理学院数学系，南京210016)

多元K－框架是K－框架的一种推广.把Hilbert空间上对于酉系统的K－框架推广到多元K－框架，引入了多元K－框架向量的概念.通过建立Hilbert空间上完全游荡向量与该空间的Parseval K－框架向量之间的关系，给出了对于酉系统的Parseval K－框架向量的一些性质.

多元K－框架;多元K－框架向量;酉系统

1 预备知识

下面给出本文需要的几个预备知识.

定义1［4］一个序列⊂H称为Hilbert空间H的框架，如果存在正数a，b，使得

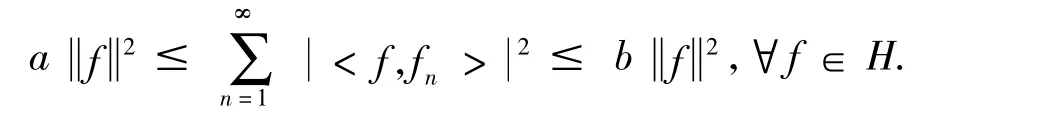
下面介绍在框架理论中起重要作用的三个算子.

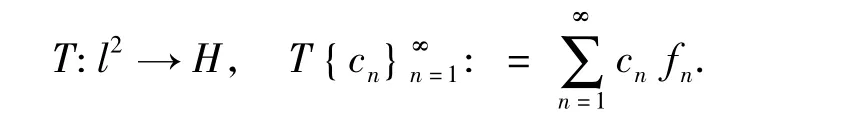
其分析算子可定义为

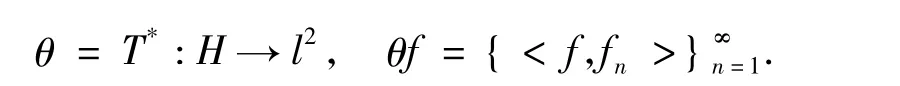
通过定义的T，T*可以得到框架算子

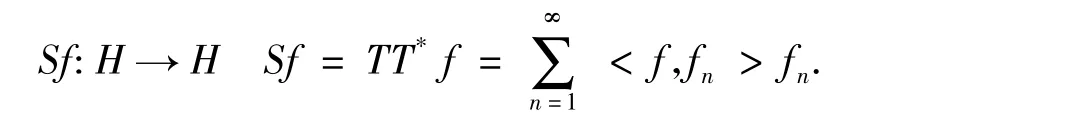
定义2［6］设K∈B(H)，称⊂H是K－框架，如果存在a，b＞0，满足:⊂H是一个紧K－框架，如果存在a＞0满足:特别地，当a=1时⊂H是一个Parseval K－框架.

定义3［9］设X，Y是两个Hilbert空间，Q∈B(X，Y)是闭值域算子，若QQ+Q=Q，则称Q+为Q的伪逆.特别地，QQ+f=Qf，∀f∈R(Q).

上述定义中伪逆Q+不具有唯一性.下面给出伪逆满足唯一性需要满足的条件.

引理1［9］设Q∈B(X，Y)是闭值域算子，Q的伪逆Q+:Y→X唯一存在的充要条件为:

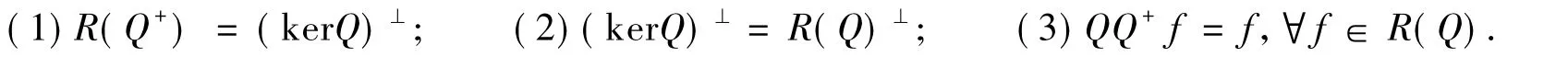
本文中用到的伪逆均满足唯一性的条件.

2 酉系统多元K－框架定义及主要定理

酉系统U是作用于可分Hilbert空间上酉算子的子集，并且包含了恒等算子I，因此一个酉群是一种特殊的酉系统.

定义4［7］一个关于酉系统U的r－元游荡向量满足:H中的元素Ψr={ψ1，ψ2，…，ψr}使得UΨr={Uψ1，Uψ2，…，Uψr:U∈U}是一个正交集合成立，其中 ＜Uψi，Vψj＞=0对于U，V∈U且U≠V或者i≠j成立.如果UΨr是H的正交基，那么Ψr被称为关于U的r－元完全游荡向量.所有的r－元完全游荡向量组的集合可以记为Wr(U).

定义5［7］U是一个作用于H的酉系统，若UΓr={Uη1，Uη2，…，Uηr:U∈U}是Uη1，Uη2，…，Uηr:U∈U}的K－框架，那么Γr={η1，η2，…，ηr}∈H是一个关于酉系统U的多元(r－元)K－框架向量.

定义6［7］U是一个酉系统，Ψr∈Wr(U)，在Ψr的局部换位子CΨr(U)可以定义为:{T∈B(H):(TU－UT)ψi=0，i=1，2…，r，U∈U}.U的换位子可以定义为:{T∈B(H):TU=UT，∀U∈U}.

下面给出本文的两个重要结论:

定理1假设Ψr={ψ1，ψ2，…，ψr}是一个关于酉系统U的一个r－元完全游荡向量，K是一个闭值域算子，K+∈U'，那么一个r－元向量Γr={η1，η2，…，ηr}是一个关于U的多元Parseval K－框架向量当且仅当存在一个部分等距A∈CΨr(U)使得AΨr=K+Γr，即Aψi=K+ηi，其中i=1，2…，r.

证明 必要性.假设Γr={η1，η2，…，ηr}是一个关于U的多元Parseval框架向量，下面定义一个线性算子T

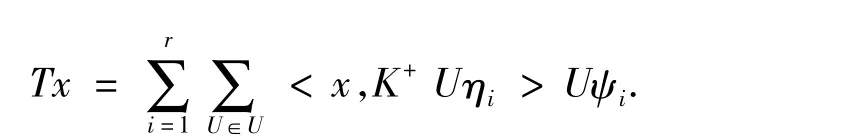
因此得到AUψi=T*PUψi=K+Uηi对∀U∈U以及i=1，2…，r，特别地，如果令U=I∈U，得到Aψi= K+ηi，其中i=1，2…，r，同时AUψi=K+Uηi=UK+ηi=UAψi对i=1，2…，r都成立，故A∈CΨr(U).

充分性.A是一个部分等距且A∈CΨr(U)，令Aψi=K+ηi，其中i=1，2…，r.因为A的终空间是AH，因此A*是一个部分等距算子，其始空间为AH，故A*在AH上是等距的，因此，对∀x∈AH，可以得到

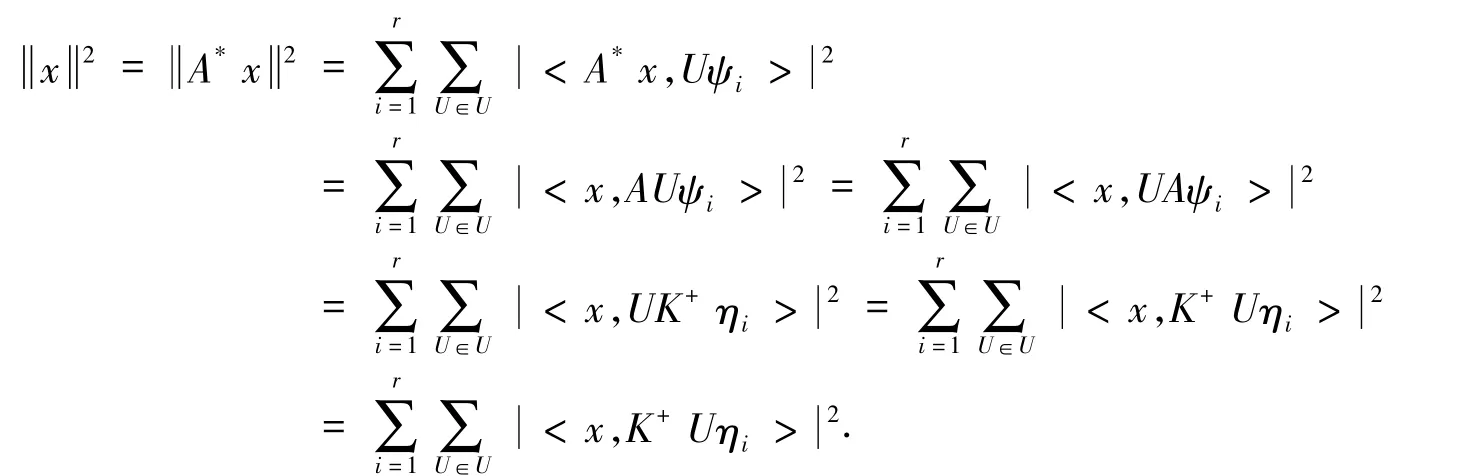
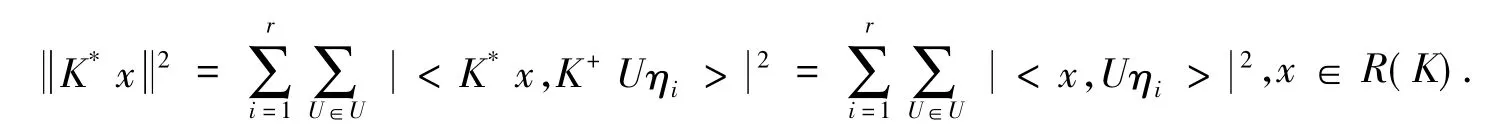
故结论得证，r－元向量Γr={η1，η2，…，ηr}是一个关于U的多元ParsevalK－框架向量.

那么对于一般的多元K－框架向量会得到一个类似的结果吗?答案是能得到这样的一个结果，同样需要加上几个条件才能得到想要的结果，得到以下定理.

定理2假设Ψr={ψ1，ψ2，…，ψr}是一个关于酉系统U的一个r－元完全游荡向量，K是一个闭值域算子，K+∈U'，那么一个r－元向量Γr={η1，η2，…，ηr}是一个关于U的多元K－框架向量，其框架界为a，b当且仅当存在一个算子A∈CΨr(U)使得AΨr=K+Γr，即Aψi=K+ηi，其中i=1，2…，r.并且aP≤AA*≤b K+2P.

证明 必要性.假设Γr={η1，η2，…，ηr}是一个关于U的多元K－框架向量，定义一个线性算子B

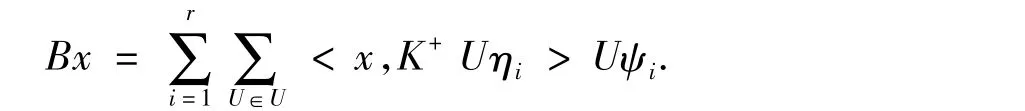
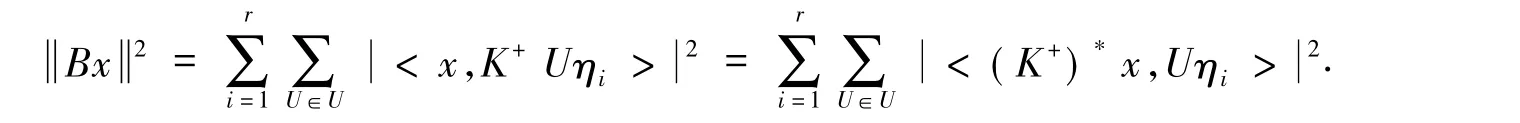
对于x∈span(K+UΓr)，又因为Γr={η1，η2，…，ηr}的框架界为a，b.可以得到

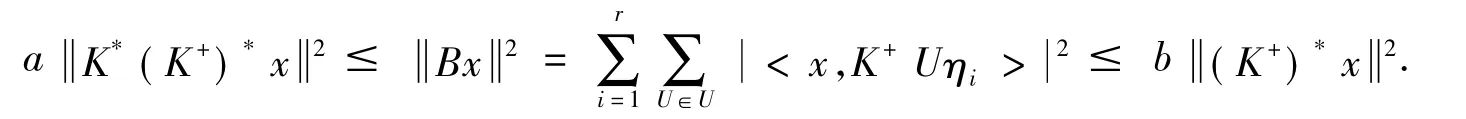
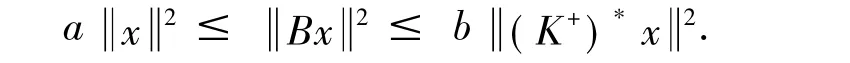
因此得到B是一个下有界的算子且有闭值域BH.即B:H→BH是一个可逆算子，令Q是一个从H到BH的正交投影，对∀U，V∈U以及i=1，2…，r，可以得到

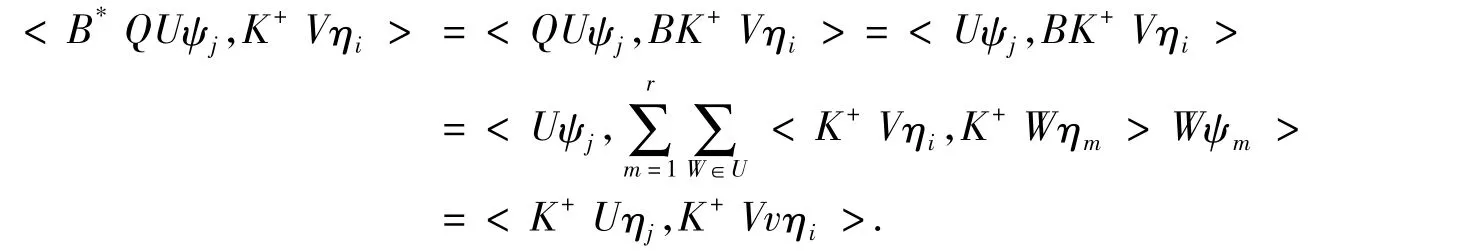
因此B*QUψj=K+Uηj，对∀U∈U成立，其中j=1，2…，r.令A=B*Q，可以得到AUψj=K+Uηj，对∀U∈U成立，其中j=1，2…，r.特别地，得到Aψj=K+ηj，对j=1，2…，r成立.因此AUψj=UAψj，对∀U∈U成立，其中j=1，2…，r.故A∈CΨr(U).因为

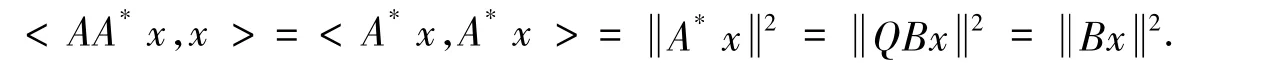
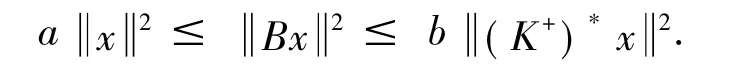
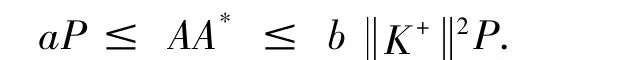
充分性.令A∈CΨr(U)使得AΨr=Γr，即Aψi=K+ηi，其中i=1，2…，r.并且aP≤AA*≤b.那么

因为aP≤AA*≤b K+2P对某一个正交投影P成立，对∀x∈PH

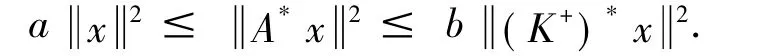
因此对∀x∈PH，得到

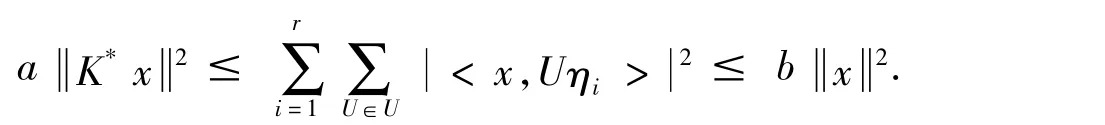
即r－重向量Γr={η1，η2，…，ηr}是一个关于U的多元K－框架向量，其框架界为a，b.

［1］DUFFIN R J，SCHAEFFER A C.A class of nonharmonic Fourier series［J］.Trans.Amer.Math.Soc.，1952，72:341－366.

［2］DAUBECHIES I，GROSSMANN A，MEYER Y.Painless nonorthogonal expansions［J］.J.Math.Phys.，1986，27:1271－1283.

［3］CHRISTENSEN O.An introduction to frames and Riesz bases［M］.Boston:Birkhauser，2003.

［4］HAN D，LARSON D R.Frames，bases and group representations［J］.Mem.Amer.Math.Soc.，2000，147(697):1－94.

［5］HAN D，LARSON D R，LIU B，et al.Operator－valued measures，dilations and the theory of Frames［J］.Mem.Amer.Math. Soc.，2014，229(1075):1－84.

［6］XIAO X，ZHU Y，GAVRUTA L.Some properties of K－frames in Hilbert spaces［J］.Results Math.，2013，63:1243－1255.

［7］GUO X.Multi－frame vectors for unitary systems［J］.Indian J.Pure Appl.Math.，2012，43(4):391－409.

［8］DAIX，LARSON D R.Wandering vectors for unitary systems and orthogonal wavelets［J］.Mem.Amer.Math.Soc.，1998，134(640):1－86.

［9］CHRISTENSEN O.Frames and pseudo－inverse［J］.Math Anal Appl，1995，191:401－414.

［责任编辑 王新奇］

K－Frame Vector for the Unitary System

ZHENG Shuai

(Department of Mathematics，School of Science，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

Multi－K－frame is an extension of K－frame.This study extends K－frame on Hilbert space to themulti－K－frame for unitary systems and definesmulti－K－frame vector.By establishing the correlations between the complete wandering r－tuple vectors and the Parseval multi－K－frame vectors，we describe some properties of the Parsevalmulti－K－frame vectors.

multi－K－frame;multi－K－frame vector;unitary system

1008－5564(2015)01－0010－04

O177.1

A

1946年，D.Gabor在研究信号处理的时候，将一个信号基于某些基本信号进行了分解.D.Gabor的这种思想很快成为与时间—频率方法相联系的谱分析范例，例如，短时Fourier变换和Wiener变换. 1952年，R.J.Duffin和A.G.Schaeffer在研究非调和Fourier分析时，进一步提炼了D.Gabor的思想方法，引入了Hilbert空间中框架的概念［1］.但直到1986年，由于I.Daubechies等人的工作［2］才受到广泛关注;自此之后，人们对框架理论及其应用进行了深入研究，并取得一系列重要研究成果，见文献［3－5］及其所列文献.框架作为Hilbert空间正交基或Riesz基的一种推广，使得空间中任意元素可以被框架元素的线性组合表示，并且这种表示可以不唯一，正因如此，使其在实际应用中具有许多优于基的地方.目前，框架在小波分析及其应用研究中得到迅速发展，已被广泛应用于信号和图像处理，无线电通讯，数据压缩，可靠性分析等许多领域.

本文将应用文献［4］的思想方法，将Hilbert空间上的K－框架与酉系统结合起来，引入并研究酉系统的多元K－框架向量，通过建立酉系统的完全游荡向量与Parseval多元K－框架向量之间的关系，引出了对于酉系统的Parseval多元K－框架向量的一些性质.

本文采用如下记号:设H为一个可分Hilbert空间，I是H上的恒等算子.对Hilbert空间H1，H2，用B (H1，H2)表示从H1到H2的全体有界线性算子的集合，并记B(H)=B(H，H).设T∈B(H1，H2)，用R (T)表示T的值域，kerT表示T的核空间，T*表示T的共扼算子.

2014－10－16

郑 帅(1989—)，男，山东淄博人，南京航空航天大学理学院数学系硕士研究生，主要从事泛函分析研究.