K－框架扰动的新结果

张旭东，孟 彬

(南京航空航天大学理学院数学系，南京210016)

K－框架扰动的新结果

张旭东，孟 彬

(南京航空航天大学理学院数学系，南京210016)

研究了K－框架扰动稳定性，并给出了1系数扰动和3系数扰动的新结果.关键词:K－框架;Bessel序列;扰动

在Hilbert空间中，框架的概念最早由Duffin和Schaeffer［1］在1952年研究非调和Fourier级数时正式提出的.小波分析诞生以后，框架理论得到了迅速的发展［2－3］，如在信号与图像处理，滤波器理论，系统模型，编码和传输等都起到了极其重要的作用［4－6］.

Hilbert空间中的K－框架［7］由Gavruta提出，它与原子系统之间存在着密切的关系，是一种比Hilbert空间的框架更一般的框架.Gavruta把框架需要满足的条件限制在有界线性算子K的值域上，而不是整个空间或闭子空间，并讨论了K－框架的一些性质［7－9］.

本文给出了Bessel序列在特定条件下为K－框架的一个结论以及给出了一般的1系数K－框架扰动和一个特殊的3系数K－框架扰动结论.

本文采用如下记号:H为一个可分的Hilbert空间;L(H)表示从H到H的有界线性算子的全体.K*表示K的共轭算子，l2表示满足＜+∞的复数列全体构成的一个无穷维复Hilbert空间.

1 主要定理及证明

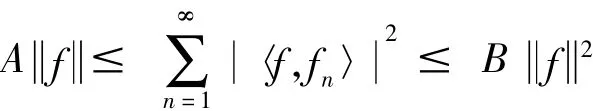
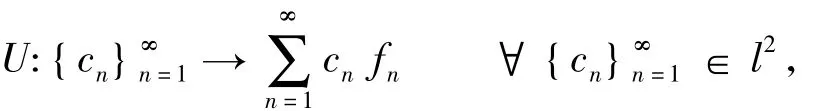
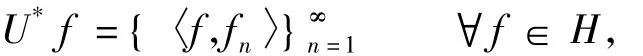
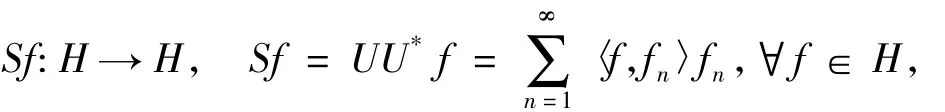
定义2［7］设K∈L(H).序列⊂H称为H的K－框架，如果存在常数A，B＞0使得对∀f∈H有

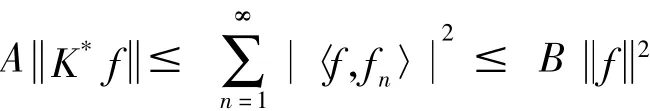
成立，分别称A，B为{fn}的下界，上界.

定义3［10］设K∈L(H)，称序列为H的紧K－框架，如果存在正数A，使得对于∀f∈H有

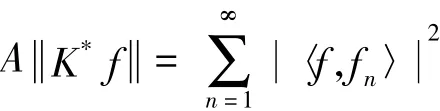
成立，称A为紧K－框架的界.

引理1［7］设K∈L(H)，序列⊂H，则下列叙述等价:

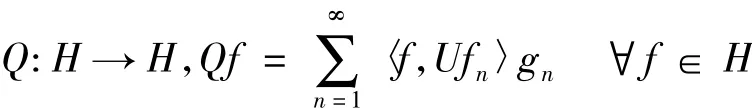
则

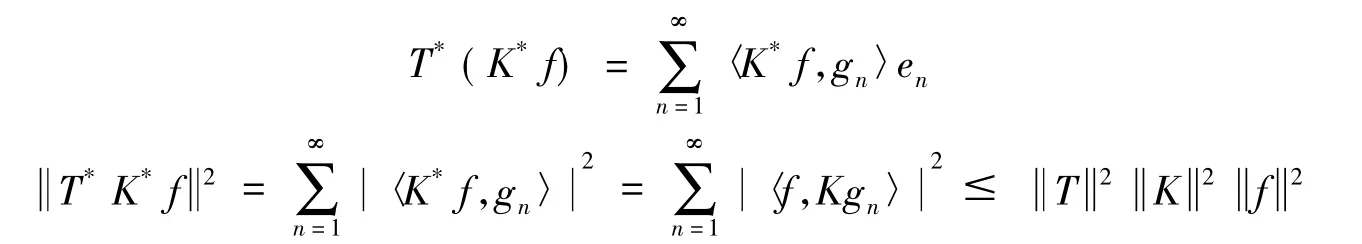
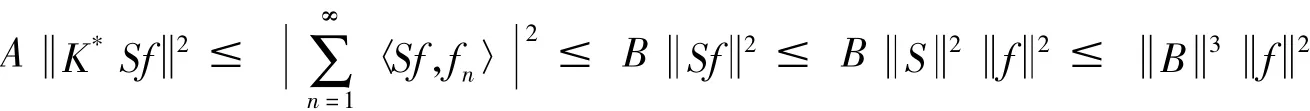
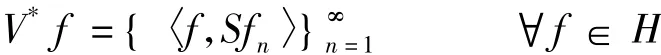
所以Q有界，又Q可逆，因此由开映射定理可知Q－1也有界，从而对于∀f∈H有:

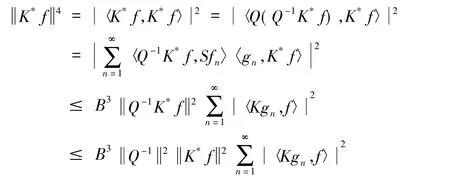
接着给出了一般的1系数K－框架扰动结论.

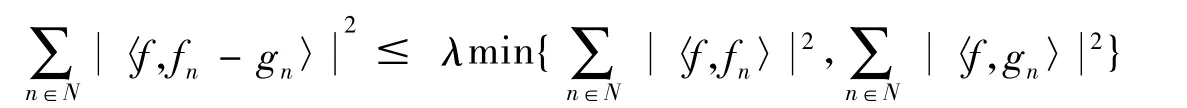
证明 因为对于任意的向量f∈H有

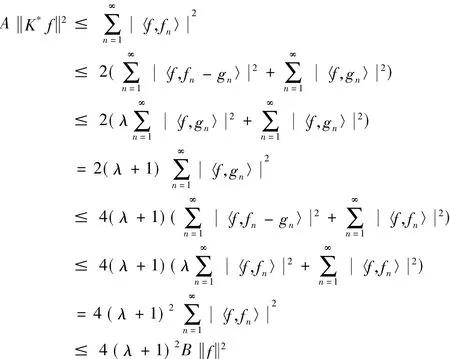
即

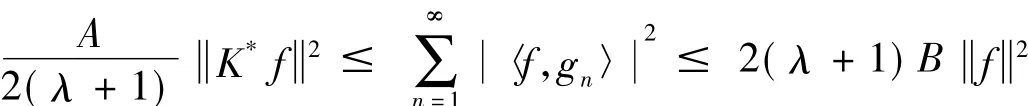
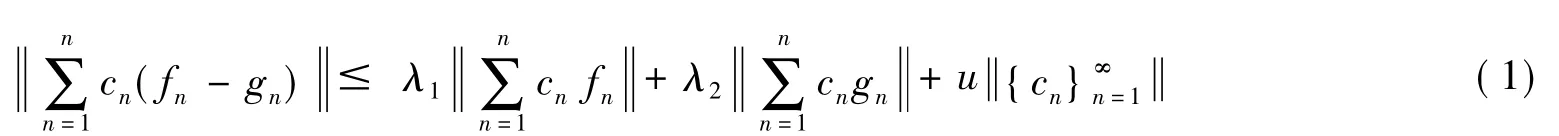
对于所有c1，…，cn(n∈N)都成立，那么是H的一个K－框架，并且其上、下界分别为

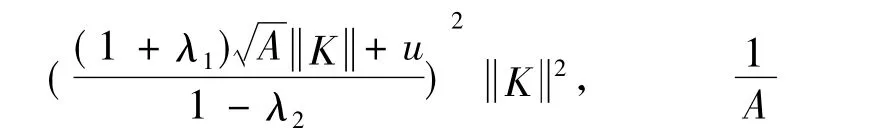
证明 因为{fn}∞n=1是一个紧K－框架，定义一个有界线性算子:

所以

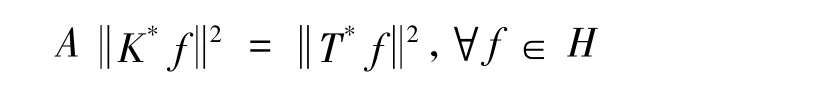
因此

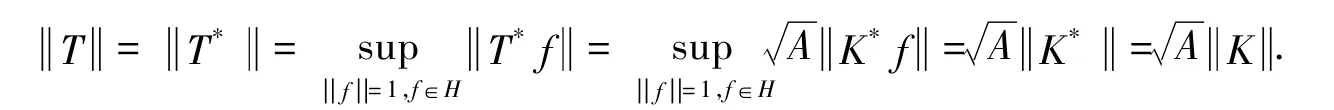
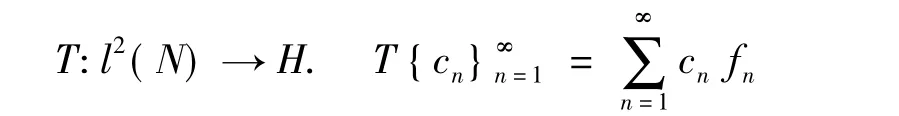
由(1)可得:

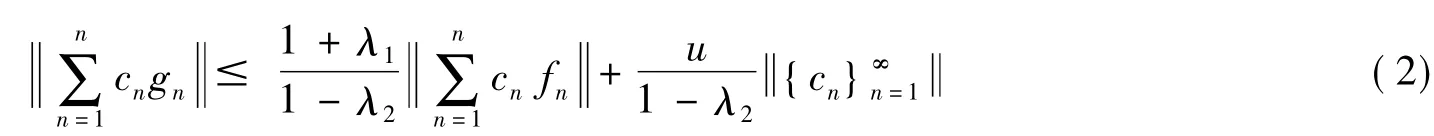
我们可以定义一个有界算子:

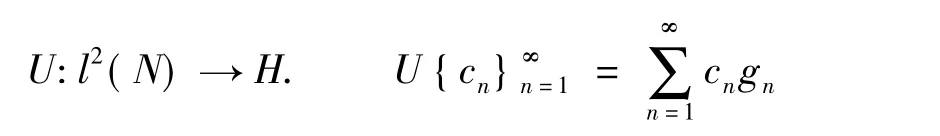
因此(2)可变为:

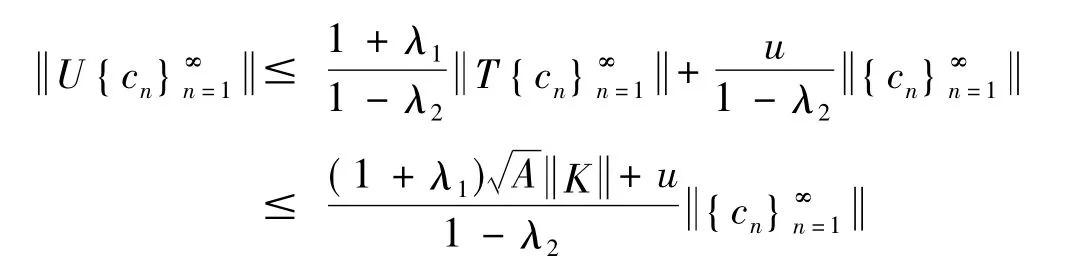
因此

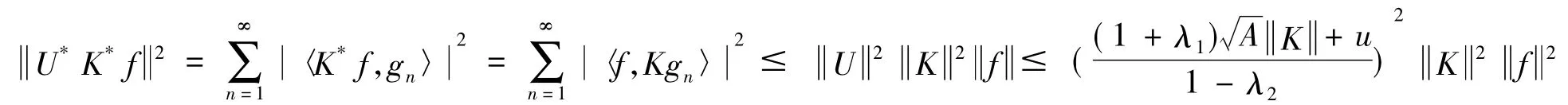
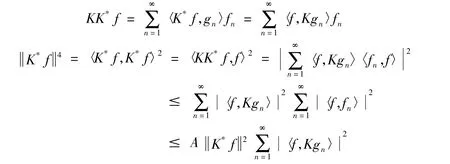
因此

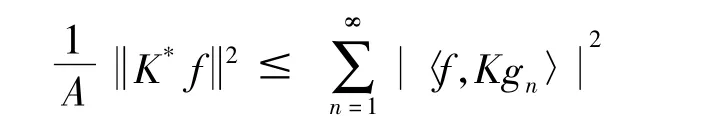
证得A－1为其下界，所以为H上的K－框架.

［1］DUFFIN R J，SCHAEFFER A C.A class of nonharmonic Fourier series［J］.Trans Amer Math Soc，1952，72:341－366.

［2］DAUBECHIES.Ten Lectures on Wavelets［M］.Philadelphia:SIAM，1992.

［3］CHRISTENSEN O.An Introduction to Frames andRiesz Bases［M］.Boston:Birkhauser，2002.

［4］FEICHTINGER H G，STROHMER T.Gabor Analysis and Algorithms:Theory and Application［M］.Boston:Birkhauser，1998.

［5］FEICHTINGER H G，STROHMER T.Advances in Gabor Analysis［J］.Boston:Birkhauser，2003.

［6］GASAZZA PG.Modern tools for Weyl－Heisenberg(Gabor)frame theory［J］.Adv Imag Elect Phys，2001，115(1):1－127.

［7］GAVRUTA L.Frames for operators［J］.Appl Comp Harm Anal，2012，32:139－144.

［8］GAVRUTA L.Perturbation of K－frames［J］.Bul St Univ Politehnica Timisoara，2011，56(70):48－53.

［9］GAVRUTA L.New results on frames for operators［J］.Proc.Intern.Conf.Sciences，11－12 Nov.2011，Oradea，Accpted.

［10］丁明玲，肖祥春，曾晓明.Hilbert空间中的紧K－框架［J］.数学学报，2013，56(1):105－112.

［11］李登峰，杨利军.Hilbert空间上框架扰动的新结果［J］.数学物理学报，2008，28A(3):489－499.

［12］肖春祥，丁明玲，李婵娟，等.K－框架的冗余和扰动［J］.福州大学学报:自然科学版，2013，41(2):143－147.

［责任编辑 王新奇］

New Outcome on Perturbation of K－Frames

ZHANG Xu－dong，MENG Bin

(Department of Mathematics，School of Science，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

This paper addresses the perturbation of K－frame.We have obtained new perturbation resultswith coefficient one and coefficient three for K－frames.

K－frames;Bessel sequence;perturbation

1008－5564(2015)01－0006－04

O177.2

A

2014－10－16

国家自然科学基金项目(NO.11171151)

张旭东(1989—)，男，江苏南京人，南京航空航天大学理学院数学系硕士研究生，主要从事泛函分析研究.