论如何在教学中体现高等数学的应用性与现实性

欧阳正勇

（佛山科学技术学院 计算科学与数学系，广东 佛山528000）

论如何在教学中体现高等数学的应用性与现实性

欧阳正勇

（佛山科学技术学院 计算科学与数学系，广东 佛山528000）

摘要：针对许多高校学生发出的高等数学无用论调，笔者从教材的结构模式、学科专业特点和教学方式等几个方面对高等数学教学内容、教学方式和方法进行创新，用以说明数学应该在各学科教学中展现现实性和应用性.由点及面，对普通高校的高等数学课程的改革提供参考.

关键词：高等数学；教学改革；应用性；现实性

数学作为一门基础学科，往往被人认为是脱离实际的空中楼阁，大部分人没有认识到数学的实用性，认为数学是数学家无聊发明出来的东西，而不知数学本身来源于实际生活，也能更好的服务于科学生产.在人类历史的发展中，原始算术的出现、欧几里德几何的形成、十七世纪微积分的诞生和现代计算机科学的实现，数学无不显示着对现实社会的促进作用.以航海交通领域为例，大到全球的GPS卫星定位,小到一个个港口物流公司的管理运作，数学无所不在.但是数学在当今时代各个领域内的实在作用，尤其在高校中,却经常受到质疑.在高科技技术发展的光环背后，《高等数学》成了一门可有可无的课程.

要改变这种状况,笔者作为高校的数学教师从以下几个方面,说明数学在各学科教学中展现的现实性.由点及面，对于普通高校的高等数学课程的改革给予参考.

1　改变传统教材的结构模式

原有传统高等数学课程的学科体系让学生失去思考的主动性.传统教材由定义--定理--定理证明--理论应用，让学生认为数学理论与应用是理所当然产生的，是数学家闲来无聊论证的，所谓应用也是由理论出发去寻找合适的应用的.而事实上，绝大部分的数学问题来源于现实，由于具备现实普遍性，人们才利用数学符号与公式抽象化解决问题.而且数学理论建立也都是建立在数学家们艰苦卓绝的努力上的.也就是说，在学习高等数学时，如果从实际问题出发，或从科学家解决问题的思路出发，对于培养学生思考问题、解决问题的能力是有很大提高的.从实际问题出发，到实际问题的解决，再到新问题的产生，这样不断循环提高，让学生在高等数学课堂上不再被动的接受枯燥的理论，而是着眼于具体问题的解决方法和实际应用，学习解决问题的方法［1］.

这需要教师对教学内容进行合理调整，对教材的依赖性较小，对教师的知识背景与能力要求较高.按传统的高等数学课程章节的知识点分类，提供大量的数学模型，将知识点穿插在模型中，让学生在解决实际问题中掌握知识点.

引入matlab、mathmatica等数学软件技术，将大大提高数学的实用性与可操作性.

2　将数学与专业学习相结合

将数学模型引入课堂是比较可行的办法.将知识点按应用分类，根据学生自身专业建立数学模型，比如物流、国际贸易专业应多准备相关经济类的问题建立数学模型，工程机械类专业准备工程类的数学模型.整个高等数学课程由几个循序渐进的数学模型来构建，并与专业知识挂钩，对学生的职业技术能力与知识素养有极大的提高.如何将理解数学概念落实到用数学思想和数学概念消化并吸收应用到工程概念与原理上.例如“案例驱动”是最好的将理论与实践结合的方法［2］.

2.1案例1

我们把易拉罐看作是一个圆柱体，是否发现百事可乐、可口可乐、健力宝等等饮料公司出售的易拉罐的半径与高之比是多少？请测量一下，并思考为什么这些公司会选取这样的比例尺寸？

工业设计在考虑外包装美观与运输便利的同时，务必考虑在容积一定的情况下所用材料最少、焊接加工等制作费用最低的成本问题，这类问题就是数学上最常见的优化问题：最值问题.

2.2案例2

2006年以来，面对中国国内房价暴涨，经济学家预测：2012年中国房价将会出现拐点.试解释这句话的意思.拐点是曲线凹凸的分界点，描述曲线增减速度的变化.经济学家预测房价出现拐点对应前期房价的高速增长，意味着房价的增长速度将会放缓.

这些案例和练习都可以具有针对性的面向不同专业的学生，引起学生对本专业的学习兴趣，加深对数学基础知识的理解，使基础课程与专业应用相呼应.

3　体现教学方法的多样性

希腊历史学家Plutarch说“思想不是一个需要填充的容器，而是需要点燃的木头”，教师需要花更多的时间点燃学生们的创造力、想象力和解决问题的能力.不能将高等数学仅仅看作是理论基础课，对于大部分应用型本科院校高等数学更多的侧重于应用数学方面，而不是理论研究.作为应用数学必然与多学科交叉应用，并利用计算机辅助教学，重视Matlab、Mathmatica等数学软件的学习，学习数学思想重于学习数学知识，学习数学方法重于学习数学理论，学习数学工具重于理论推导，将数学知识跟计算机能力有机结合.压缩理论课时，增加上机课时.布置论文或报告形式的作业.考试考查方面应更多的侧重应用能力，通过积极地与学生交流，不断调整教学方式.比如让学生建模后上机计算,利用计算机辅助手段解决数学问题与应用问题是当今世界高校潮流趋势.

3.1案例(线性规划模型的实例)

家具公司生产桌子和椅子，用于生产的劳力共计450个工时，木材共有4立方米,每张桌子要使用15个工时，0.2立方木材，售价80元.每张椅子使用10个工时，0.05立方木材，售价45元.问为达到最大的收益，应如何安排生产？

案例分析：

（1）案例求什么？

①生产多少桌子？x1张桌子

②生产多少椅子？x2张椅子

（2）案例优化什么？

收益最大值Maxf=80x1+45x2

（3）实际的限制条件是什么？

原料总量0.2x1+0.05x2≤4

劳力总数15x1+10x2≤450

3.2建立模型

以产值为目标取得最大收益.设：生产桌子x1张、椅子x2张(决策变量)，将目标优化为：Maxf=80x1+ 45x2.

对决策变量的约束：

3.3模型求解

3.3.1方法（1）图解法（用于决策变量是2维）

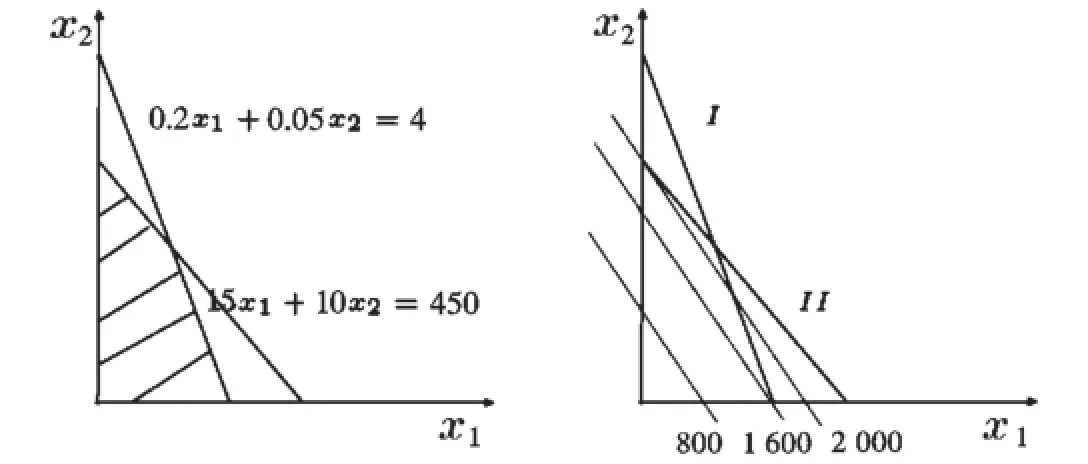
图1　线性规划模型实例

线性规划问题的目标函数(关于不同的目标值是一族平行直线)目标值的大小描述了直线离原点的远近,并且最优解一定在可行解集的某个极点上达到［3］(穿过可行域的目标直线组中最远离或接近原点的直线所穿过的凸多边形的顶点).

3.3.2方法（2）用EXCEL—Solver实现

模型中的数据直接输入EXCEL工作表中（见图2）.其中决策变量初始的值可以任意给出，它们是可变的，软件最后将给出最优解的值.SUMPRODUCT是EXCEL的一个内置函数，表示两个向量或矩阵对应元素乘积的和.

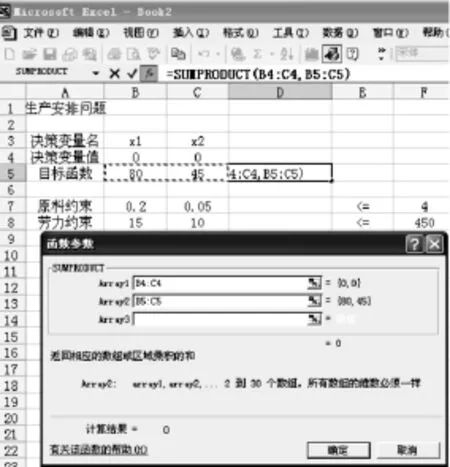
图2　数据输入

接下来选择工具菜单中的规划求解，即可得到最优解为2 200.

3.3.3方法（3）用Matlab实现--lp线性优化函数

线性优化问题即目标函数和约束条件均为线性函数的问题.其标准形式为：

其中A∈Rm×n,m≤n（通常m＜n），b∈Rn,c∈Rn均为数值矩阵.

将Maxf=80x1+45x2,

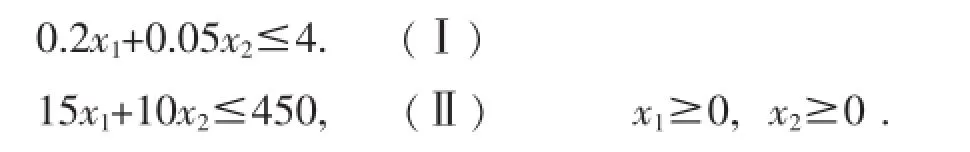
转化为Minf=-80x1-45x2,

Sub.to0.2x1+0.05x2≤4.

程序如下：

c=［-80,-45］;a=［0.2,0.05;15,10］;b=［4,450］;vlb=［0,20］;vub=［0,45］;

［x,lam］=lp(c,a,b,vlb,vub)（参数vlb,vub给出变量的上下边界的约束）.

说明：x的解为最优解，lam说明约束条件发挥了作用.

3.3.4方法（3）用LINDO实现

我们可以直接在下面的窗口输入LP模型［5］.见图3.

图3　输入简单的优化模型

输入后，用鼠标单击LINDO软件工具栏中的图标，或从菜单中选择Solve│Solve(Ctrsl+S)命令，则LINDO开始编译这个模型，编译没错误马上开始求解，求解时会显示LINDO求解器运行状态窗口，里面的“Objective”对应的数字2 200就是最优解.

这个例子中的LP模型太小了，我们可能还没来得及看清结果输出的界面，最优解就出来了，并马上弹出询问你是否需要作灵敏性分析的对话框，可以先选择“否N”按钮，这个窗口就会关闭.如果你在屏幕上没有看到求解的结果，那么可以用鼠标选择LINDO的主菜单 “Window”,会发现有一个子菜单项“Reports Window”，这就是最终结果的报告窗口.用鼠标选择“Window│Reports Window”，就可以查看到窗口的内容（见图4）.

图4　最优解及各变量的取值

“LP OPTIMUM FOUND AT STEP 2”表示单纯形法在两次迭代后得到最优解.“OBJECTIVE FUNCTION VALUE 1)2 200.000”表示最优目标值为2 200.000（在LINDO中目标函数所在的行总是被认为是第1行，这就是这里“1）”的含义）.

“VALUE”给出最优解中各变量的值：x1=14.000 000，x2=24.000 000.“SLACK OR SURPLUS（松弛或剩余）”给出约束对应的松弛变量的值：第2、3行松弛变量均为0，说明对于最优解来讲，两个约束均取等号，即都是紧约束.“DUAL PRICES”给出对偶价格的值.“NO.ITERATIONS=2”表示用单纯形法进行了两次迭代（旋转）.

上面这个案例充分的体现了数学课程的多变、灵活、实用的特性.

高等数学课程应着眼于提高学生的以下几方面能力：（1）对数学的整体性和知识点在现代数学中的位置及在经济发展中的直接和间接用途有所了解、有所认识.（2）从实际问题中抽象出各类数学问题的能力. （3）能从多角度观察问题，能用多种方法解决问题.

在我国大力发展教育事业的大背景下，数学作为一门基础课程对各应用学科都起着极其重要的现实作用.然而“以学生为中心”的课程教学模式没有理想中那么简单，是要学生在已有的知识结构上通过吸收外来信息最终建构个人体系.特别是对于在传统教学模式中成长起来的教师们来说，转变教学模式是一个长期的缓慢的甚至可能会出现反复的过程.

课程教学模式改革的趋势之一是向应用型本科教育方向发展，高等数学课程的教学改革也必将迎来新一轮的挑战.笔者在借鉴国内外先进的教学理念的基础之上，结合我国高校教育的特点，通过对高等数学课程的教学模式改革与研究，以求建立一种创新、有效的教学模式.这种教学模式，应当体现创新教育教学的特色，追求教学的实际效益，既要适应学生的实际，又要适应社会实际的需求，要有明确的岗位能力目标；要教会学生完整地做好一件事情，让学生由“学会”变为“会学”；强调学生的能力培养，评价标准着重衡量学生的能力水平.笔者旨在通过对教学模式的研究与实践，促进高等数学教育教学质量提高，也为本科院校开展教育改革研究提供一些有益借鉴与参考.

参考文献：

［1］张霞,张庚家.用问题激发学生学习高等数学兴趣的研究［J］.大学数学,2006,22(2):23-25.

［2］杨曙光.高等数学应用问题教学探索［J］.高等数学研究,2014,17（4）：119-122.

［3］姜启源，谢金星，叶俊.数学模型［M］.第三版.北京：高等教育出版社,2005.

［4］王沫然.MATLAB 5.X与科学计算［M］.北京：清华大学出版社,2000.

［5］谢金星，薛毅.优化建模与LINDO/LINGO软件［M］.北京：清华大学出版社,2005.

［6］王爱华.新形势下改进高等数学教学实践与探索［J］.教育与职业,2013(24）：119-121.

（责任编辑：李婉）

中图分类号：O13

文献标识码：A

文章编号：1007-5348（2015）02-0073-06

［收稿日期］2014-09-21

［基金项目］广东省教改项目（GDJG20141204）.

［作者简介］欧阳正勇（1978-），男，湖北汉川人，佛山科学技术学院计算科学与数学系讲师，博士；研究方向：主要从事微分方程.

How to Show Application and Reality of Higher Mathematics in Teaching

OUYANG Zheng-yong
（Department of Mathematics,Foshan University,Foshan,528000，Guangdong,China）

Abstract:For useless argument of higher mathematics from many students in university,this paper proposes innovation of higher mathematics teaching content and teaching ways from several aspects such as structure model,characteristics of subjects and teaching methods and so on,which can be used to explain that the mathematics should show the reality and application in the teaching.And from the point to surface,it could provide reference for reform of higher mathematics curriculum in colleges and universities.

Key words:higher mathematics;teaching reform;application;reality