GPS卫星星历仿真
2015-08-01崔立鲁
崔立鲁
(成都大学 建筑与土木工程学院,四川 成都 610106)
0 引 言
随着卫星导航系统及相关应用越来越广泛,人们对卫星导航定位的要求也越来越高.一个可靠性高、适用性强、计算精度高的数据处理软件直接决定了导航定位的解算精度.而检验数据处理软件最有效的方法是利用卫星仿真数据进行验算,其中卫星星历的仿真极为重要.目前,国外已有相关研究机构开展了这方面的研究[1-2],而国内也有一些科研机构开始对GPS 仿真进行研究[3-5],但相关GPS 仿真方法的研究和文献还比较少.鉴于此,本研究简要地阐述了GPS 卫星广播星历的仿真原理,利用卫星参数数据对该卫星广播星历数据实现仿真模拟,并与真实的广播星历进行比较,验证了该仿真原理的可靠性和适用性,实现了卫星仿真的关键性步骤.
1 GPS 广播星历仿真
1.1 广播星历参数
GPS 广播星历由一系列参数组成,这些参数以开普勒轨道参数为基础,再加上一些表示轨道蛇洞的调和系数及随时间的变率,共有16 个:一个参考时刻,6 个相应参考时刻的开普勒轨道参数,9 个反映摄动力影响的参数.这些变率在仿真广播星历时以RINEX 格式输出,具体参数如表1 所示.
表1 中,各参数的具体含义为:TOC 为时间参数,参考时刻的年、月、日、时、分、秒;a0为卫星钟误差的常数项,单位s;a1为卫星钟误差的变化速率,单位s/s;a2为a1的变化速率,单位s/s2;IODE 为星历数据的年龄,单位s;Crs为在轨径向方向上周期改正正弦项的振幅,单位m;Δn 为平均角速度的长期变化率,单位rad/s;M0为参考时刻的平近点角,单位rad;Cuc为在轨道延迹方向上周期改正余弦项的振幅,单位rad;e 为卫星轨道的离心率;Cus为在轨道延迹方向上周期改正正弦项的振幅,单位rad为卫星轨道长半轴的平方根,单位In V2;t0为星历参考时刻所在星期中的秒数,单位s;Cic为轨道倾角周期改正余弦项的振幅,单位rad;Ω0为参考时刻升交点赤径的主项,单位rad;Cis为轨道倾角周期改正正弦项的振幅,单位rad;i0参考时刻轨道倾角,单位rad;Crc为在轨道径向方向上周期改正正弦项的振幅,单位m;ω 为近地点角距,单位rad;Ω·为升交点赤径在赤道平面中的长期变化,单位rad/s;i 为轨道倾角变化率,单位rad/s;IODC 为卫星钟数据年龄,单位s.
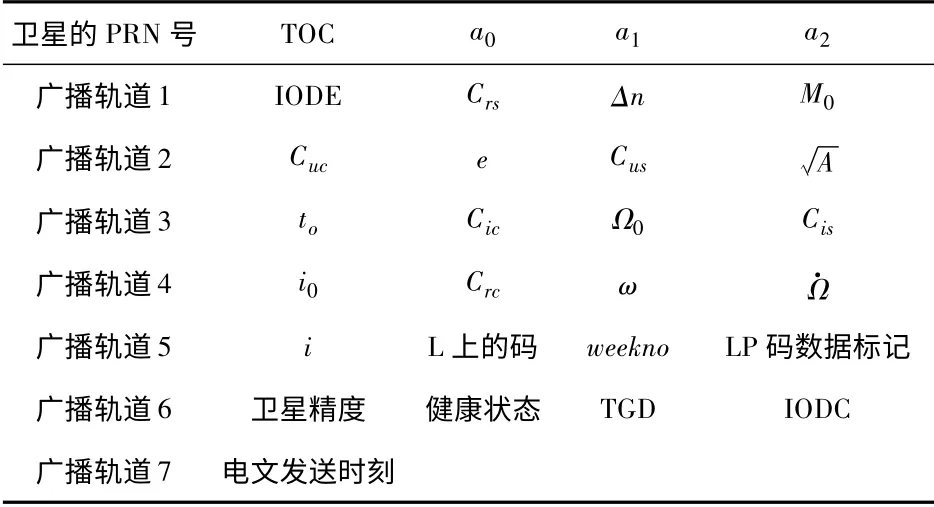
表1 广播星历轨道及各轨道参数
1.2 星历参数仿真模型
1.2.1 时间参数生成模型.
星历文件中的时间参数包括GPST 周计数weekno、获得星历参数时刻t0、星历数据年龄IODE、卫星钟数据年龄IODC 等.其中,weekno 和t0均需要根据UTC 来生成.令UTC 时间为tUTC,它与GPST 起始时刻所对应的起始时刻之间相隔的星期数为WUTC,同时考虑模拟所在时刻的时区为Tzone,则,
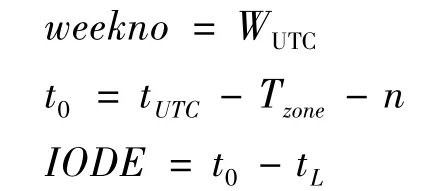
其中,n 为UTC 与GPST 之间的跳秒数,toc是卫星导航电文中第一子帧的参考时刻,t1是计算时刻改正数所作测量的最后观测时刻.由于在本研究的仿真过程中主要基于软件方法的实现,所以后2 个参数均置零.
1.2.2 时钟改正数生成模型.
本研究在仿真计算时,对星历文件中的3 个时钟改正参数,钟偏a0、钟漂a1、钟频a2,按照下述关系进行计算,设定参考时刻的3 个参数为,则有,
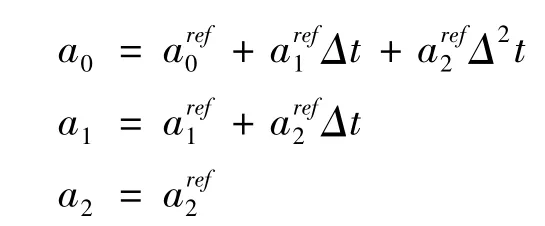
在本研究中,这3 个参数设置为零.
1.2.3 轨道参数的生成.
根据求得的惯性坐标系下卫星的位置和速度求解卫星初始时刻的6 个开普勒轨道根数.
1)根数a,e,M 的计算.
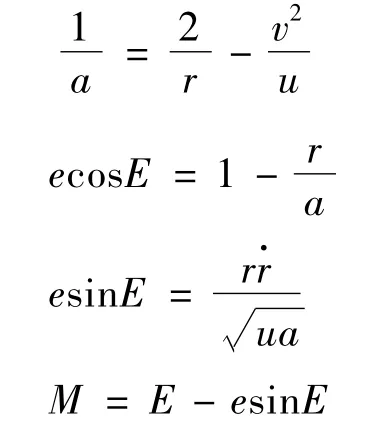
其中,
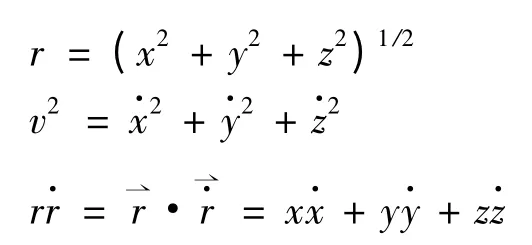
2)3 个定向i,Ω,ω 根数的计算.
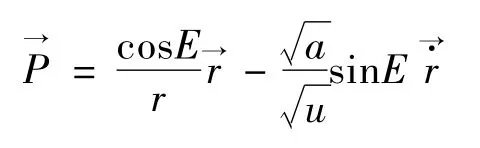
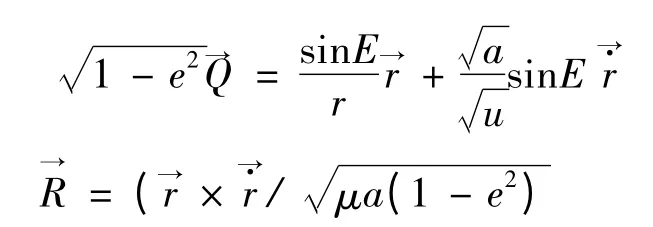
Pz= sinisinω,
Qz= sinicosω,
Rx= sinisinΩ,
Ry= sinicosΩ,
Rz= cosi
根据上面5 个式子可解出,
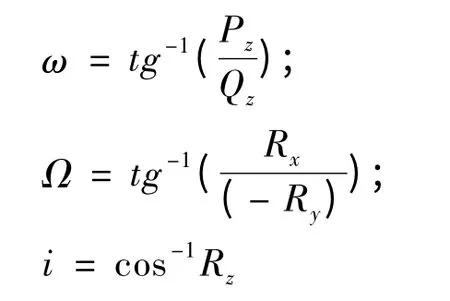
2 仿真数据计算和分析
2.1 计算方法
开普勒轨道根数拟合是一迭代收敛的过程,初值的选取对迭代结果具有一定的影响.首先计算参考时刻卫星对应的惯性系下的位置速度,然后以二体问题的方法求解初始6 个开普勒轨道根数,并将轨道根数转化到需要的地固坐标系中作为初值,将其余9 个摄动调和参数初值设为0,其具体计算方法如下:①根据读取的精密星历插值求出任意时刻卫星的位置和速度;②将地固系下的toe时刻卫星状态矢量,通过极移、岁差和章动逆向变换到J2000 坐标系,求得在J2000 下的开普勒轨道根数;③将升交点赤经Ω 与参考时刻格林尼治恒星时CAST 组差,得到地固系下的初始轨道根数;④由卫星在惯性系下的坐标与速度计算卫星在初始时刻的6 个开普勒轨道根数;⑤计算出的6 个开普勒轨道根数及9 个摄动项参数(初值设为0),计算卫星的近似坐标及误差方程系数阵(通过求导得到),并列出误差方程;⑥由最小二乘法迭代求解15 个参数.
2.2 试验数据比较
本研究计算了3 号卫星从1月31日开始到2月12日连续13 d 的每历元时刻的瞬时轨道参数.表2为3 号卫星第一组平差计算所得第一个历元时刻的瞬时轨道参数,表3 为3 号卫星广播星历中第一个历元时刻的瞬时轨道参数,从这两个表中数据对比可以看出求解的6 个开普勒轨道根数与9 个摄动项参数的差异.
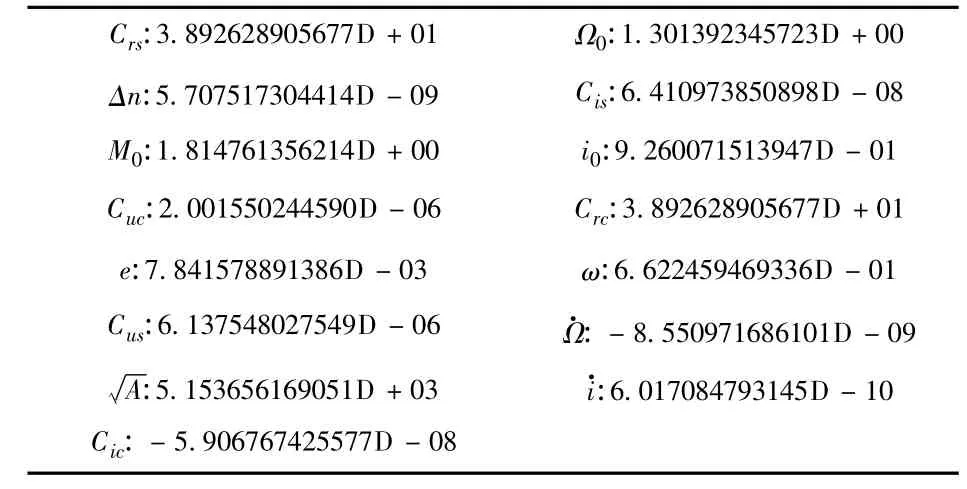
表2 3 号卫星第一组平差计算所得第一历元时刻的瞬时轨道参数
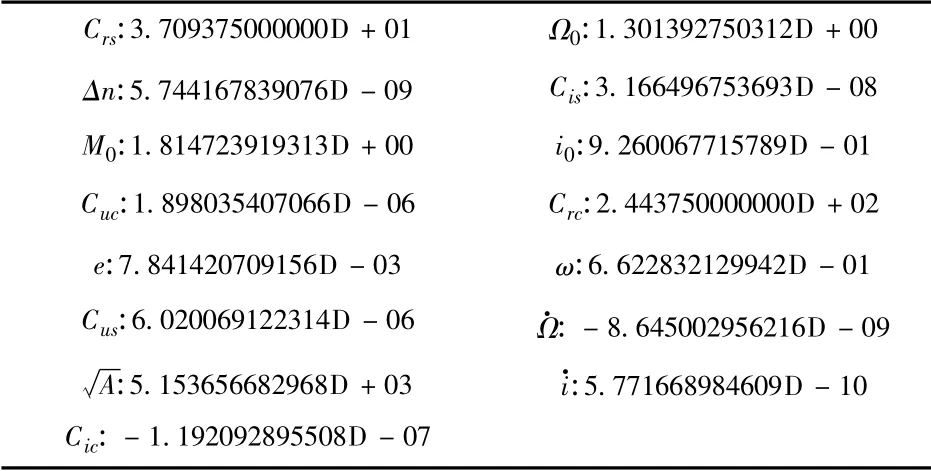
表3 3 号卫星广播星历中第一历元时刻的瞬时轨道参数
从求出的第一历元的广播星历参数与实际接收机所接收到的广播星历数据比较可以看出,各参数之间差异很小,对个别摄动参数差别较大的数据进行替换计算,其对卫星位置的影响在分米级以内.
表4 是根据求出的参数计算出卫星位置与精密星历中卫星位置求差所得的数值.
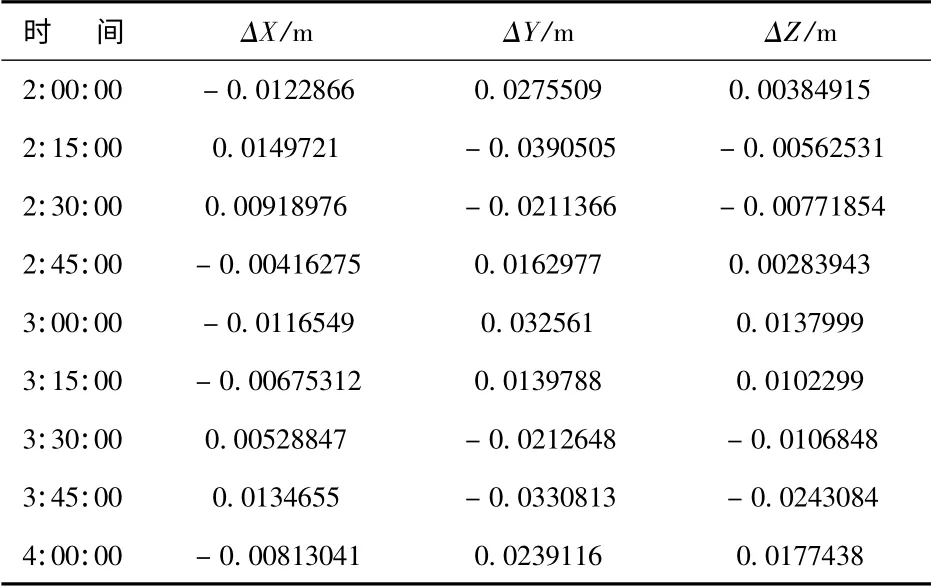
表4 精密星历与仿真星历计算出的卫星位置差值
表4 数据表明,按上述方法求解共15 个参数,由9 个历元计算得到的轨道曲线基本上通过每个历元的卫星位置,计算得到的轨道与卫星真实轨道基本一致.
图1、图2 给出了仿真星历的3 个参数与接收机接收到的广播星历中对应的3 个参数的差值,这2颗卫星分别为PRN3、PRN8.图1、图2 中,纵坐标的单位为rad,时间区间为1月31日到4月12日,数据对应的时刻为每日的02:00 时.
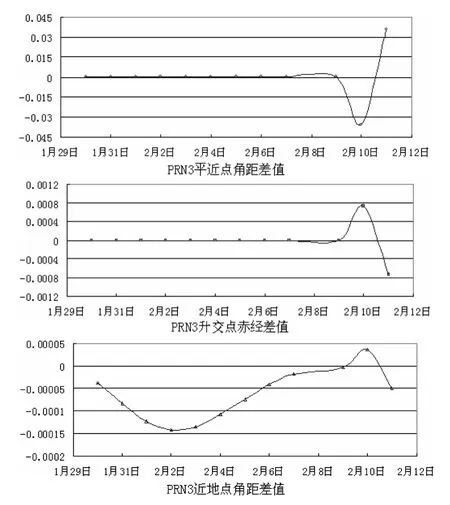
图1 PRN3 模拟的3 个参数与实际参数差值曲线图
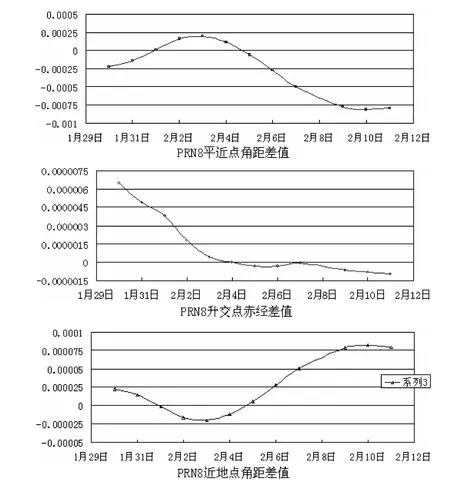
图2 PRN8 模拟的3 个参数与实际参数差值曲线图
从图1、2 可知,仿真星历的3 个参数M0、Ω、ω 值与接收机接收到的广播星历中的M0、Ω、ω 值之差在一定范围内波动,但在所列图中个历元参数计算出的卫星位置与精密星历中卫星位置差值都在厘米级.由此可知,仿真星历能够满足检验数据软件算法的需要.
3 结 论
GPS 卫星星历仿真是GPS 卫星仿真中比较重要的一个环节,也是验证卫星数据处理软件的重要依据.本研究主要介绍了GPS 卫星广播星历仿真的基本原理,并将仿真数据与真实数据进行了比较,利用仿真数据计算出相应的卫星位置数据并与真实卫星位置数据进行了比较.数据比较的结果表明:利用本研究提出的卫星星历仿真方法计算得到的卫星位置数据能够较好地反应真实卫星的情况,有助于卫星数据处理软件的验证.
[1]Kouba J,Héroux P.Precise point positioning using IGS orbit and lock products[J].GPS Sol,2002,5(2):101-106
[2]许其凤.GPS 卫星导航与精密定轨[M].北京:解放军出版社,1994.
[3]崔立鲁,何秀凤,罗志才,等.Galileo 系统定位性能仿真模拟分析[J].测绘信息与工程,2007,32(4):10-12.
[4]崔立鲁,罗志才,钟波,等.观测噪声对频域输入输出法数据融合的影响[J].大地测量与地球动力学,2009,29(1):79-82.
[5]崔立鲁.重力卫星加速度数据的插值算法研究[J].测绘工程,2012,21(3):21-25.
