壁湍流SL标度律相关参数的实验分析

张 珂

(安徽广播电视大学 城建学院，安徽 合肥 230001)

0 引 言

湍流又称紊流，是普遍存在于自然界中的一种随流速不同而变化多端的流动现象，同时这种流动状态也给工程技术带来了很多困扰.目前，许多相关领域的学者在研究分析湍流的性质和运动规律，以寻求解决现实工程中遇到的湍流问题的方法.研究发现，近壁面处湍流的能量占据了总湍流的大部分，对整个湍流的发生和维持起重大的作用，因而对近壁面湍流的研究至关重要.一般认为，标度律［1］(也叫尺度律)是在全尺度空间和时间中，利用统计相似性的原理，对所有尺度的湍流脉动量进行相似性统计.由于各项同性湍流的特殊性，它的标度律被分析得最为详尽.其中线性标度律(K41 标度律)是较早被研究提出的一种的标度律，它是由Kolmogorov［2］在1941年根据局部各向同性假设而获得的;奇异标度律［3］是由Kolmogorov 对线性标度律进行修正研究获得的;ESS 标度律是Benzi 等［4－5］在1993年通过对圆柱尾流、自由射流进行测量后研究发现的;SL 标度律是我国著名学者佘振苏和他的学生Leveque 在1994年共同提出的，这种标度律是基于层次结构模型［6－7］(一种刻画湍流脉动结构的新的模型)得到的;1999年，Benzi 等［8］以各种标度律理论研究为基础，对位于湍流边界层的不同壁面位置的速度结构函数进行统计分析，提出一个假设并得到一种新的p 阶结构函数与二阶结构函数及耗散率的新形式标度律;2002年，Jacob［9］利用热线实验(HWA)对新形式标度律进行了实验验证，并分别用三阶结构函数和二阶结构函数代替奇异标度律中的r，使p 阶结构函数变得更为简单，从而得到了2 种形式标度律的另一种表现形式，并对其进行了实验验证.

1 SL 标度律与相关参数介绍

SL 标度律的层次结构模型［6－7］认为:尺度、相干度和幅度皆不相同的层次结构构成了湍流，最强间歇结构(即最大振幅和最强相干度的结构)不间断的分布在从积分尺度到耗散尺度的每个尺度上，幅度很小的结构根据特定的层次对称关系和最强间歇结构联系起来，层次模型就是如此的连接着多尺度和脉动结构.

通过对相关结构量进行无量纲分析，再由层次结构理论的基本假设作为基础，结合奇异标度律，进而得出层次结构模型SL 标度律标度指数的公式，

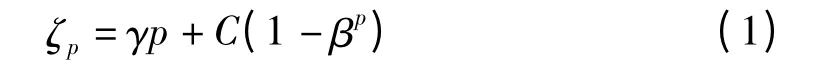
式中，γ 代表速度结构函数最奇异标度指数，也就是最高激发态的标度指数;β 代表间歇参数;λ =3γ－1代表能量耗散率的最奇异标度指数，也就是最强能量耗散率的标度指数.当湍流处于均匀各向同性时，速度结构函数的标度指数公式可以写成，

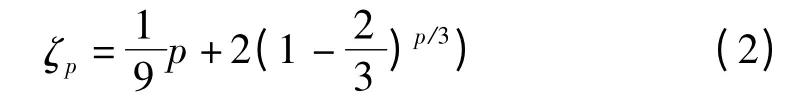
对SL 标度律而言，当假设湍流是各项同性时，SL 标度律中的γ、β 及C 均为常数，而实际的湍流边界层的变化是十分复杂的，不能将γ、β 及C当作常量处理.对此，本研究利用实验数据对SL 标度律的参数γ、β 进行拟合分析.

2 实验设备与相关参数

本研究在对实验段相关数据的测量时运用PIV系统来实现的.PIV 系统［10］是一种较为先进的流动测量技术，现已广泛地应用在流体力学测量中.实际的实验装备由PIV 系统和实验水槽构成，其中，CCD相机、激光器、同步器、帧采集器以及计算机组成了PIV 系统.

图1 是实验水槽和试验段的示意图.实验水槽的长度为1 300 mm，宽度为142 mm，实验时水槽中水的深度为90 mm.为了达到较好的实验目的，5 cm长的方格蜂窝器被安装在实验段的上游的收缩段之前，实验段的下游安装驱动水泵，整个实验段的上部未密封，来流的湍流度被降低了.同时实验段的水面是自由表面，没有压力梯度，满足实验要求.在实验中所用示踪粒子为直径12 μm 的空心玻璃球，它的跟随性较好，能够满足实验的要求.

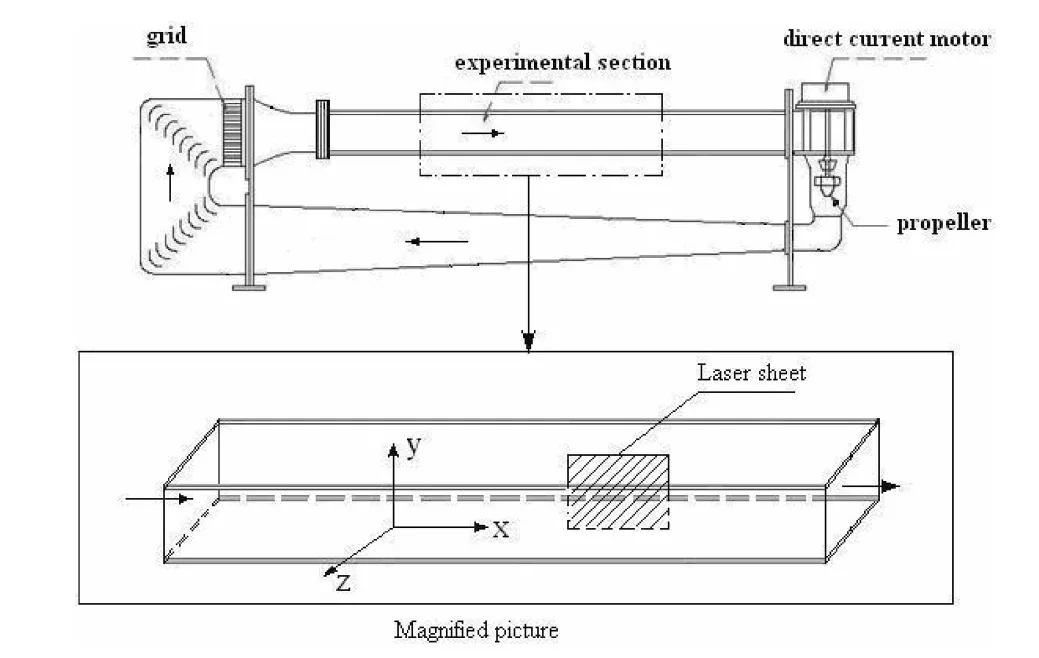
图1 实验水槽及实验段示意图

实验在二维平面(图1 中的xy 平面)内进行的，x 方向为平行于平板并沿着平均流动的方向，y 方向为垂直平板的方向.实验时，水槽的自由流速度为0.35 m/s，摩擦速度u*=0.014587 m/s，动量厚度θ=0.007697 m，Reθ是以动量损失厚度和主流速度表示的雷诺数，Reθ=2 694.质询窗大小为16 ×16像素，在400 μs 的脉冲间隔下，能够识别的最大速度为0.41 m/s，图像场(即采集域)大小为1 472像素×1 088像素，处理得到的速度矢量场大小同为92×68(即x 方向92 个矢量，y 方向68 个矢量)，每个矢量对应一个质询窗，采样频率为每秒钟15 幅图，对应7.5 幅矢量图，采集的速度矢量样本为2 500幅.

图2 是实验所得的平均速度曲线与Spalding 剖面的对比图.可明显看出，图中两条曲线比较吻合，说明当地的边界层速度分布与充分发展的湍流边界层速度分布在近壁面区非常相似，可以认为实验段的湍流边界层已经达到充分发展，符合实验条件.

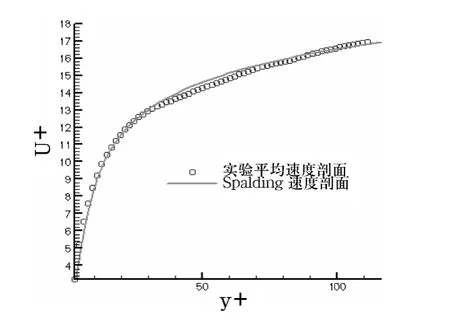
图2 Reθ =2 694 时的边界层平均速度剖面与Spalding 剖面比较

3 结果与分析

本研究利用ESS 标度律、广义ESS 标度律和新形式标度律3 种标度律［11］，对SL 标度律相关参数进行拟合.这3 种形式的标度指数的表达式为:

1)ESS 标度指数.

2)广义ESS 标度律的标度指数.

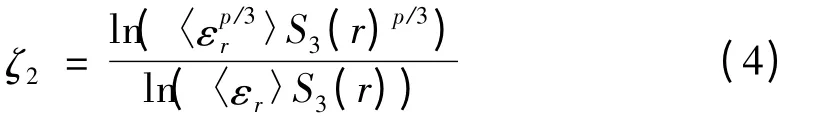
3)新形式标度律标度指数.

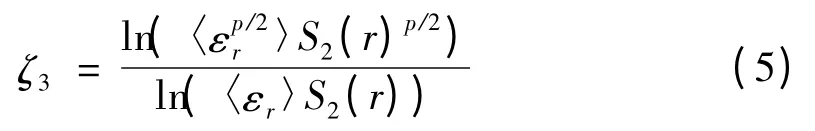
式中，Sp是脉动量的结构函数，Sp(r)=〈| u(x + r)－ u(x)|p〉=〈|u(r)|p〉，〈〉是系综平均.

4)利用文献［12］的湍流耗散率公式，

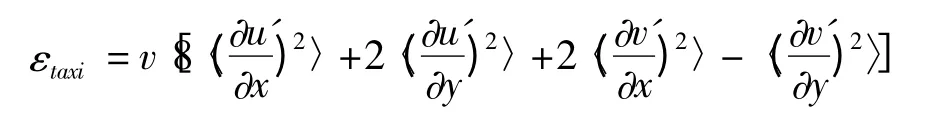
和湍流的能量耗散率公式，

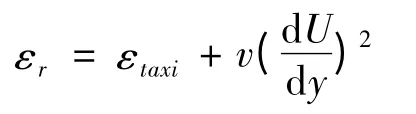
代入式(3)、(4)、(5)中对3 种形式的标度指数进行SL 标度律拟合研究，3 种形式标度指数的拟合公式为，

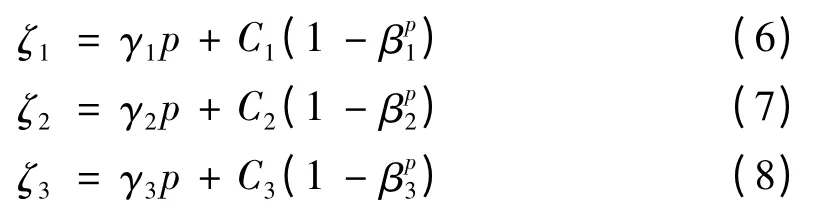
根据计算要求小波特性，对大量的速度数据采用小波分析的方法对结构进行提取和分析，然后用传统的统计学方法进行统计计算，其中小波分析应用的是双正交小波Symlet 小波，它是Matlab 包中的一种，具有很好的紧致性、正交性和对称性，能够满足计算的要求.

为了简便起见，将图3 和图4 中的图形进行以下说明，横轴代表y+，范围是0 ～120，纵轴分别代表β 和γ，圆圈代表由公式(6)的拟合结果，即β1和γ1，菱形代表公式(7)的拟合结果，即，β2和γ2，三角形代表公式(8)的拟合结果，即β3和γ3.

3.1 SL 标度律中间歇参数的变化情况

图3 给出了由流向脉动速度计算出的3 种标度指数拟合的间歇参数在不同尺度上随壁面距离y+的变化曲线.图3 显示，在小尺度a = 2dx 时，β2和β3有缓慢下降的趋势，但变化幅度不是很大，β1下降得较快.当在a = 4dx 时，β2和β3变化较为混乱，而β1相对β2和β3来讲，变化并不是很大.在a = 8dx时，β3的变化不是很稳定，β2在黏性底层时变化不大，在对数律层，y+在大约40 ～60 之间时，β2基本不变，在y+大约是在70 ～112 之间时，β2变化也较小，只是在两个区域内β2的数值相差较大.当a =16dx 时，β1大都在0.49 上下变化，β2除了少数点外，大多在0.13 上下震荡，到了y+= 80 后有上升的趋势;而β3在过渡层内变化不大，在对数律层内震荡较大.当a = 32dx 时，β1、β2和β3相对前面的尺度来讲，变化趋于稳定.从整体上看，间歇参数随着壁面距离的不同而变化，随着尺度的增加，间歇参数也在逐渐地减小，但β1相对于β2和β3而言，它的变化较小.本研究认为原因在于计算β2和β3时融入了能量耗散率，而随着尺度的差异，计算出的能量耗散率也不完全相同，湍流的很多局部特征被很好地显现出来了.上述得到的结果和文献［12］不尽相同.文献［12］运用的是HWA 测量方法，在有限的法向位置上对间歇参数进行的拟合分析，得出的结论是间歇参数不随壁面测点位置的变化而改变，在计算和拟合的过程中未说明具体的尺度参数;而在本研究中，是对实验段的整个测量范围中的全部实验数据进行分析.通过对不同位置和尺度的间歇参数的拟合研究可以看出，本研究结论与文献［13］的结论有部分是一致的，差异之处在于，在本研究中，a = 32dx 的大尺度上，在y+的一些范围内，由广义ESS 标度指数和新形式标度指数拟合得到的间歇参数是稳定的.从总体上看，随着尺度由小到大，间歇参数则整体上出现由大到小的趋势(个别点除外)，从层次相似性来讲，大尺度的层次相似性要比小尺度的层次相似性弱.

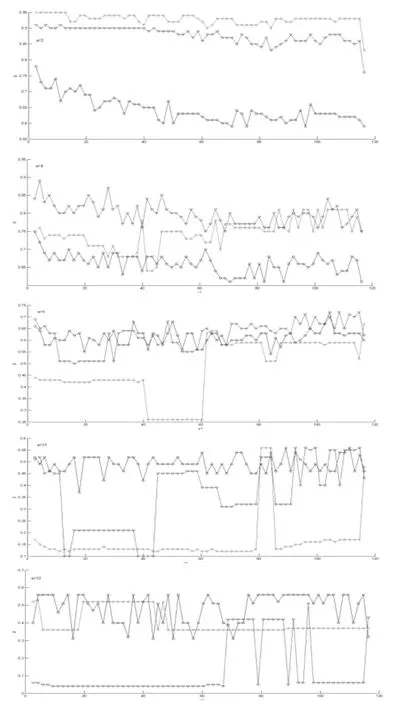
图3 不同尺度的间歇参数(β)随y+ 的变化情况

3.2 SL 标度律中速度结构函数最奇异标度指数γ的变化情况

图4 反映了最奇异标度指数γ 在不同的尺度上随壁面距离变化的曲线.图4 显示，在a = 2dx 的较小尺度上，3 个最奇异标度指数γ1、γ2和γ3的变化曲线混杂在一起，较为混乱;随着尺度的不断增加，3个最奇异标度指数都在慢慢增大，并随着壁面距离的变化逐渐趋于平缓.到了大尺度a = 32dx 时，γ2不随y+的变化而变化，为一常数，而γ1和γ3也仅仅是在各自的2 个数值上变化，且2 个的数值差别都不是很大.在3 个最奇异标度指数中，变化最明显的是γ2，在小尺度上，随着壁面距离的变化，最奇异标度指数变化混乱，到了大尺度上，最奇异标度指数不随壁面的距离变化而变化，为一常数.因此，这一运算结果也从另一方面说明了湍动能的级串过程［15］，也就是说，在整个湍流中，大尺度脉动在较少地耗散能量的同时又在不断地输出能量，就像是一个特大的蓄能池，与此不同的是，小尺度湍流则消耗掉了大尺度运送过来的动能，就像一个专门消耗能源的机械，这就是湍流的级串过程.

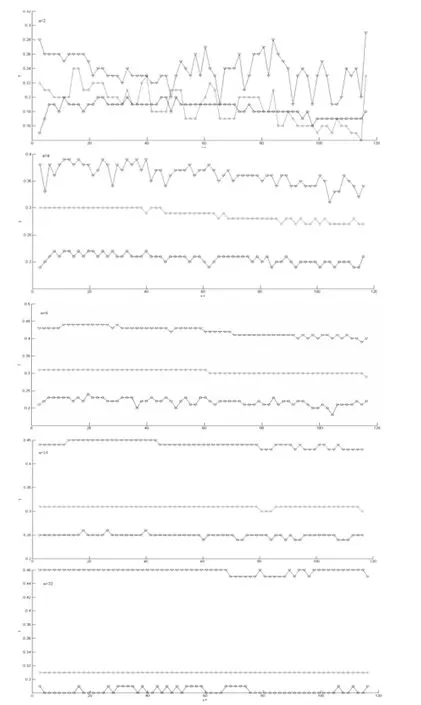
图4 不同的尺度时最奇异标度指数(γ)随y+ 的变化情况

3.3 流动结构显示

图5 反映了流向脉动速度场的原始等值线图，图6 显示了由小波分析重构后的不同尺度下流向脉动速度的等值线图.图5 是比较有代表性的湍流边界层，没有规律可循.利用小波分析重构原理，可将图5 的数据处理后得到图6.其规律呈现:在小尺度下，由于湍动能的消耗与级串等原因，通过小波分析重构后的速度等值线图仍然很杂乱，但由于尺度的变大，重构后的速度等值线图越来越明显，尤其是在大尺度a = 32dx 时，速度等值线图有剧烈震荡的位置和数值表现出明显的规律，此种变化和最奇异标度指数的变化曲线相对应，即在小尺度上，最奇异标度指数的变化较为混乱，随着尺度的增加，最奇异标度指数逐渐趋于稳定，不随壁面距离的变化而改变;受到最奇异标度指数及耗散率的作用，层次相似参数(间歇参数)的规律性变化不明显.图6 的流动图案和图5 的拟合结果是相辅相成的，这也从另一个方面验证了标度律计算的正确性，但SL 标度律的相关系数的确定还需进一步研究.

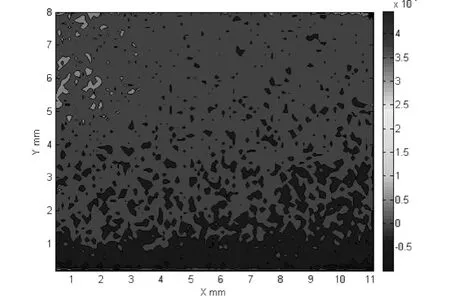
图5 流向脉动速度场的原始等值线图

图6 小波分析重构后的流向脉动速度在不同尺度上的等值线图

4 结 论

通过对上述间歇参数和最奇异标度指数的拟合研究可以看出:随着尺度的不断增加，间歇参数随壁面距离的变化逐渐趋于稳定，特别是由广义ESS 标度指数和新形式标度指数拟合计算出的间歇参数在大尺度上只是在有限的几个数值上变动，也就是说，在大尺度上，壁面距离对间歇参数的影响不大;而对于最奇异标度指数而言，随着尺度的增加，3 个最奇异标度指数慢慢平稳下来，最奇异标度指数的稳定性和尺度的大小是一致的，也就是说，在大尺度上，最奇异标度指数与壁面位置无关.就整体而言，尺度越大，间歇参数反而越小，从相似性方面讲，大尺度脉动的层次性比小尺度脉动的层次相似性小，最奇异标度指数则随着尺度的增加逐渐增大，说明大尺度脉动结构具有较多的有序成分，空间分布上也更加不平均，此从另一个方面说明了大尺度结构的相干性比小尺度结构的相干性更显著.最后，通过对不同尺度下脉动速度的小波分析和重构，并与拟合结果对比显示了标度律运算的合理性，这为后续湍流边界层标度律和相干结构的研究提供了实验依据，也为进一步解决水库滑坡，边坡稳定等工程问题提供了理论基础.

［1］Frisch U.Turbulence:The Legacy of A.N.Kolmogorov［M］.England:Cambridge University Press，1995.

［2］Kolmogorov A N.The local structure of turbulence in incompressible viscous fluid for very large reynolds number［J］.Proc R Soc Lond，1991，434(1890):15－19.

［3］Kolmogorov A N.A refinement of previous hypotheses concerning the local structure of turbulence in incompressible viscous fluid for very large Reynolds number［J］.J Fluid Mech，1962，13(1):82－85.

［4］Benzi R，Ciliberto S，Tripiccione R，et al.Extended self-similarity in turbulent flows［J］.Phys Rev E，1993，48(1):R29－R32.

［5］Benzi R，Ciliberto S，Ruiz Chavarria G，et al.Extended selfsimilarity in the dissipation range of fully developed turbulent［J］.Europhys Lett.，1993，24(4):275－279.

［6］She Z S，Leveque E.Universal scaling laws in fully developed turbulence［J］.Phys Rev Lett，1994，70(3):336－339.

［7］佘振苏，苏卫东.湍流中的层次结构和标度律［J］.力学进展，1999，29(3):289－301.

［8］Benzi R，Amati G，Casciola C M，et al.Intermittency and scaling laws for wall bounded turbulence［J］.Phys Fluids，1999，11(6):1－3.

［9］Jacob B，Olivieri A，Casciola C M.Experimental assessment of a new form of scaling law for near-wall turbulence［J］.Phys Fluids，2002，14(2):481－491.

［10］徐玉明，迟卫，莫立新.PIV 测试技术及其应用［J］.舰船科学技术，2007，29(3):101－105.

［11］张珂.壁湍流标度律及SL 标度律相关参数实验研究［D］.武汉:华中科技大学，2009.

［12］姜楠，王玉春，舒玮，等.壁面加热湍流耗散率标度指数测量的实验研究［J］.应用数学和力学，2002，23(9):921－928.

［13］赵伟.湍流边界层中相干结构及统计量SL 标度律的研究［D］.武汉:华中科技大学，2006.

［14］张兆顺.湍流［M］.北京:国防工业出版社，2002.