带形状参数的五次三角Bézier 曲线

张丹丹，吴欢欢

(安徽广播电视大学 安庆分校，安徽 安庆 246001)

0 引 言

在计算机辅助几何设计中，学者们对曲线曲面的研究做了大量的工作，像Bézier 曲线、B 样条曲线［1］.为了对曲线曲面的形状进行灵活地修改，研究者引入了形状参数，例如，文献［2］讨论了带形状参数的Bézier 曲线，通过引入一个形状参数，对曲线的形状进行调控.但Bézier 曲线在组合曲线相邻控制顶点上的连续性，有局限性.近年来，研究者开始研究三角函数空间上的曲线曲面的表示方法，例如，文献［3］首次讨论了带一个形状参数的二次三角多项式曲线及2 段三角多项式曲线的拼接问题，文献［4］研究了二阶、三阶三角函数组成的T-Bézier 曲线，其二阶曲线在拼接点处可达到G3连续，三阶曲线可达到G2连续，文献［5］讨论了带一个形状参数的T-Bézier 曲线，该曲线可表示椭圆和圆，文献［6］研究了带2 个形状参数的三次三角Bézier 曲线，通过改变参数λ1、λ2，可对曲线的形状进行局部或整体调控，文献［7］研究了带形状参数的类四次三角Bézier 曲线，给出了2 段曲线G2、G3连续的条件，该曲线还可表示椭圆、抛物线等二次曲线弧.在此基础上，本研究分析了带一个形状参数的五次三角Bézier 曲线，它具有五次Bézier 曲线类似的几何性质，并讨论了组合三角多项式曲线在拼接点处C2连续的条件，该五次三角多Bézier 曲线可精确地表示椭圆弧、圆弧、抛物线弧等.

1 基函数

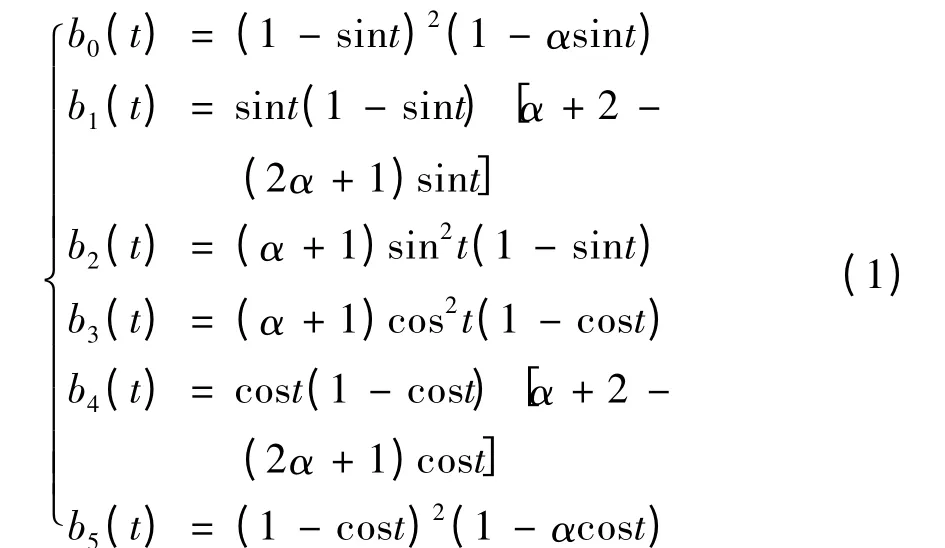
式(1)的五次三角多项式基函数具有如下性质，

1)非负性.

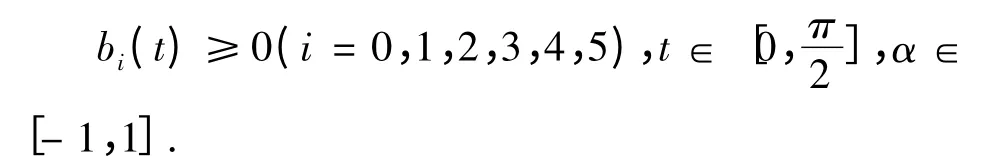
2)权性.

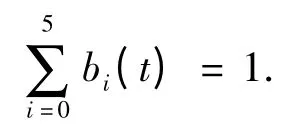
3)对称性.

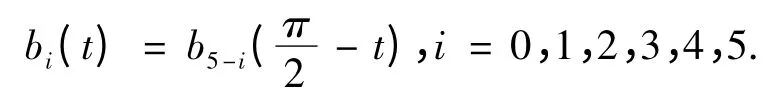
4)端点性质.

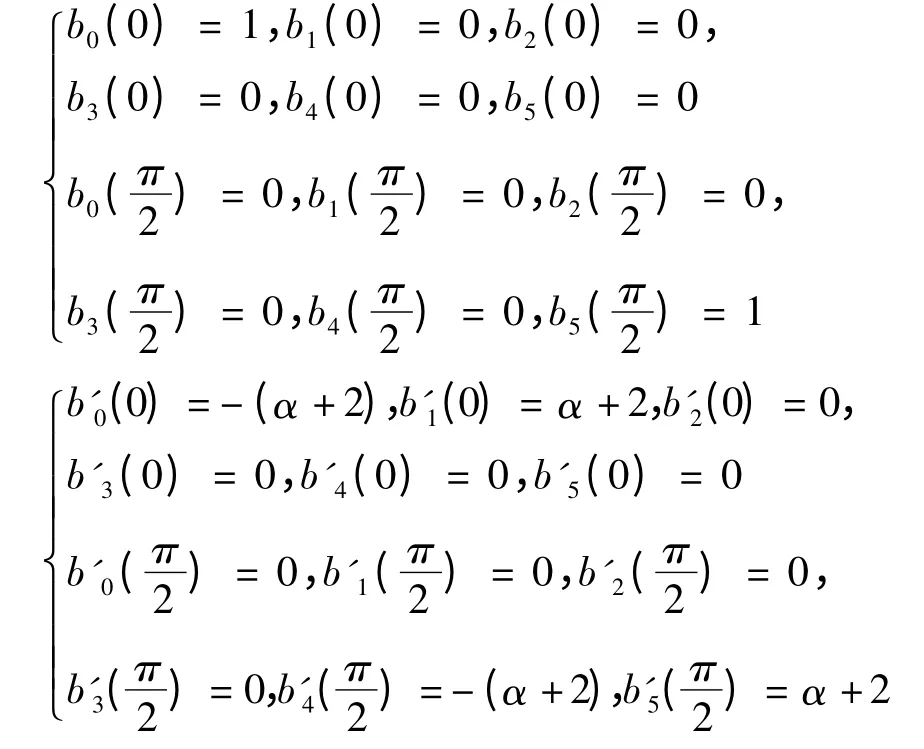
5)单调性.

当α递增时，b0(t)、b5(t)单调递减，b2(t)、b3(t)单调递增;当t ∈［0，π/6］时，b1(t)单调递增;当t ∈［π/6，π/2］时，b1(t)单调递减;当t ∈［0，π/3］时，b4(t)单调递减;当t ∈［π/3，π/2］时，b4(t)单调增减.

图1 为α = 1 时基函数图像

2 曲线与性质

定义2 给定R2或R3中的6 个控制点Pi，i =0，1，2，3，4，5，

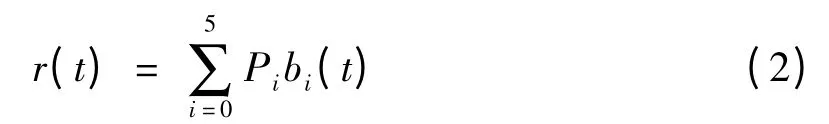
则称式(2)为带形状参数α 的五次三角Bézier 曲线.

该曲线具有下列性质:

1)端点性质.

2)对称性.

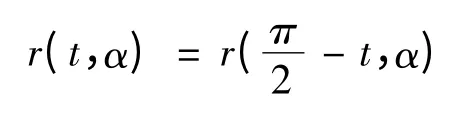
图2 为形状参数取不同值的五次三角Bézier 曲线，从上到下α 依次取1，0.5，0，－ 0.5.可发现当α增大时，曲线越逼近控制多边形.

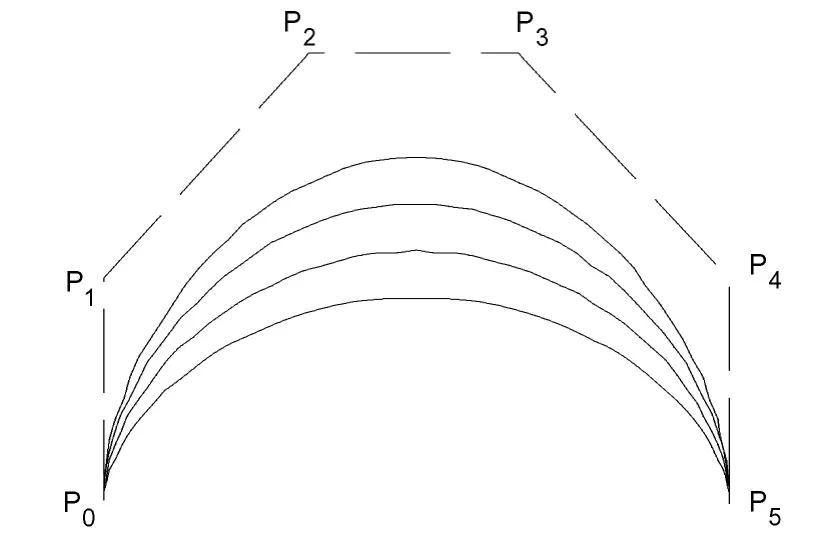
图2 取不同参数值的曲线

3 曲线的连续

设2 条曲线，

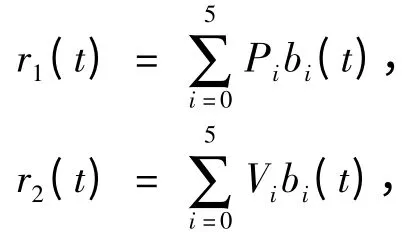
定理1 若V0V1与P4P5共线且方向相同，即，

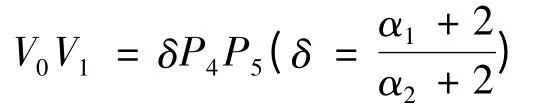
且V0= P5，则曲线r1(t)与r2(t)在连接点处C1连续.

证明

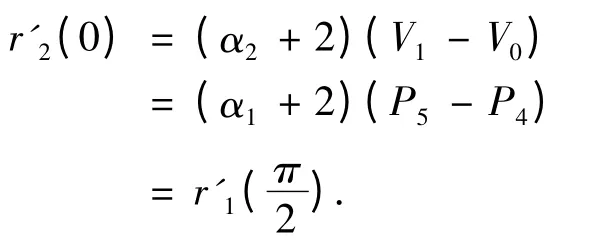
即曲线r1(t)与r2(t)在连接点处C1连续.

定理2 当α1= α2= 1 时，在C1连续的条件下，若时，则曲线r1(t)与r2(t)在连接点处C2连续.证明 当V0= P5时，

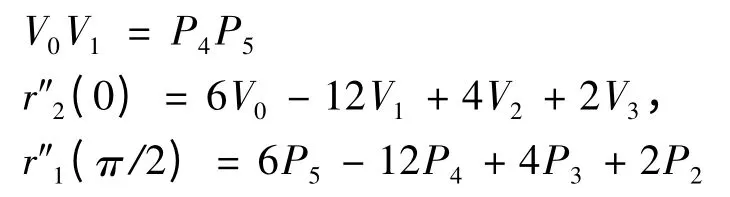
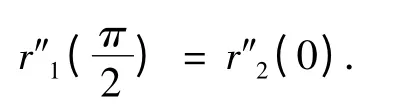
即曲线r1(t)与r2(t)在连接点处C2连续.

4 应用实例

4.1 椭圆弧、圆弧的表示

设P0，P1，P2，P3，P4，P5为控制多边形顶点，当α =时，取P0=(a，－b)，，则该五次三角Bézier曲线可表示为，

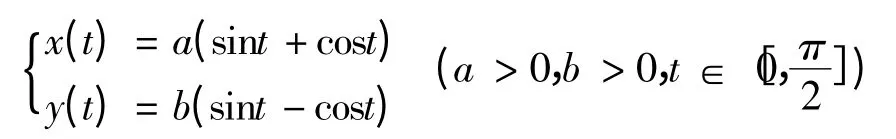
当a = b 时，该五次三角Bézier 曲线表示的是一段圆弧.图3 给出了椭圆弧的曲线表示.

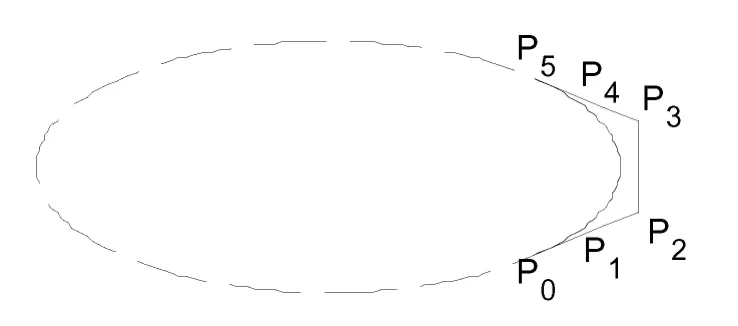
图3 椭圆弧的表示

4.2 抛物线弧的表示

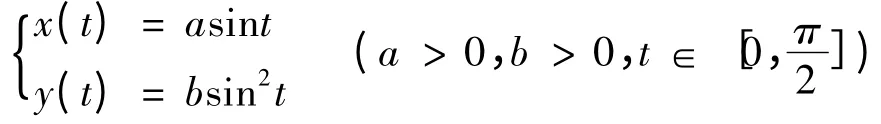
图4 给出了抛物线弧的曲线表示.

图4 抛物线的表示

4.3 花瓣图形

五次三角Bézier 曲线与五次Bézier 曲线一样，可以表示开曲线、闭曲线的模型.图5 是α = 1，0.5，0，－0.5 时的开曲线、闭曲线花瓣图形.

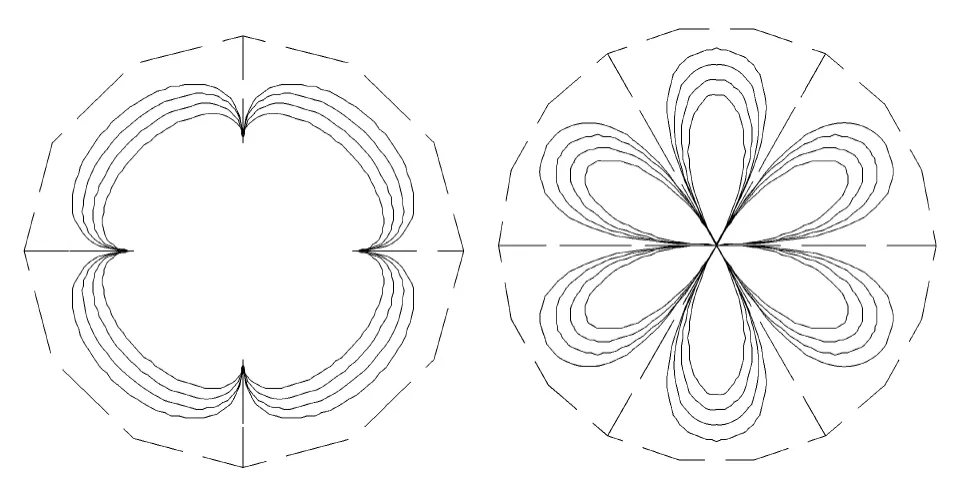
图5 花瓣图形

［1］施法中.计算机辅助几何设计与非均匀有理B 样条［M］.北京:高等教育出版社，2001.

［2］Han Xuli.Quadratic trigonometric polynomial curves with a shape parameter［J］.Comp Aided Geom Des，2002，19(7):479－502.

［3］吴晓勤.带形状参数的Bézier 曲线［J］.中国图像图形学报，2006，11(2):269－274.

［4］严兰兰，韩旭里，邬国根，等.二阶/三阶三角Bézier 曲线［J］.图学学报，2013，34(5):71－75.

［5］吴晓勤，韩旭里.带参数的二次三角Bézier 曲线［J］.工程图学学报，2008，29(1):82－87.

［6］杨联辉，邬弘毅.带形状参数的三次三角Bézier 曲线［J］.合肥工业大学学报(自然科学版)，2005，28(11):1472－1476.

［7］杨炼，李军成.一类带形状参数的类四次三角Bézier 曲线［J］.计算机工程与科学，2011，33(3):77－81.