基于分形理论的复旦人民币汇率指数的预测分析

康凤华

(南京财经大学应用数学学院，江苏南京 210046)

基于分形理论的复旦人民币汇率指数的预测分析

康凤华

(南京财经大学应用数学学院，江苏南京 210046)

运用R/S分析法和Hurst指数对复旦人民币实际有效汇率指数的结构特征进行分析，发现市场具有状态持续性和分形分布的特征;同时建立分形插值模型描绘其在一段时间内的变化规律，并预测短期内的指数走势，发现与原数据走势基本一致，且其平均标准误差仅为2.618%.结果表明，运用Hurst指数来估计垂直比例因子和利用分形插值模型预测复旦人民币汇率指数均是可行的.

分形插值;R/S分析;Hurst指数

复旦人民币汇率指数由复旦大学金融研究院主持研发，于2010年10月22日正式对外发布.该指数为贸易加权综合汇率指数，反映了人民币汇率对中国对外贸易竞争力的综合影响.复旦人民币汇率指数是按日编制并发布，不同于国际清算银行编制的人民币有效汇率指数按月编制滞后1月发布，因而提高了人民币汇率指数的及时性和动态性.目前人们对人民币汇率问题的关注主要聚焦于人民币对美元的双边汇率，谈到人民币升值或贬值就只看人民币对美元的汇率，而实际上对国际贸易影响较大的是以贸易加权的实际有效汇率，所以从宏观经济效应来看，对汇率关注的焦点应该从人民币对美元的双边汇率转移到人民币实际有效汇率上来［1］.

分形理论最早是由Mandelbrot于1967年提出，主要用来分析股票价格的波动变化.Peters等人将其引入到研究金融市场的复杂结构中，提出了分形市场假说，为进一步研究金融市场的非线性特征提供了一个新的方法.分形R/S分析法对于揭示金融市场的长期记忆性、分形统计结构等特征提供了一个稳健的分析技术.现有研究已表明，人民币汇率市场是一个具有分形和混沌结构的非线性动态复杂系统［2－3］.为了建立合理的分形插值模型对金融时间序列进行分析，本文采用了一种简单实用的计算迭代函数系垂直比例因子di的算法，并以此建立了一种仿射分形插值模型［4］.

本文以复旦人民币实际有效汇率指数为例，首先使用R/S分析法和Hurst指数分析复旦人民币指数收益率的结构特征，再由分形插值函数的分数维定理，计算出di，并据此建立能分析和预测复旦人民币指数的仿射分形插值模型，最后用matlab软件来模拟和预测复旦人民币指数的变化趋势.

1 分形理论

1.1 分形插值原理

分形插值原理是美国科学家Barnsley于1986年在迭代函数系统的基础上提出的基于拼贴原理的一种方法.对于数据集{(xn，yn):n=0，1，…，m}，其仿射变换wi具有如下形式:

令bi=0，此仿射变换wi的其余四个常数ai、ci、ei、fi可由下式得到:

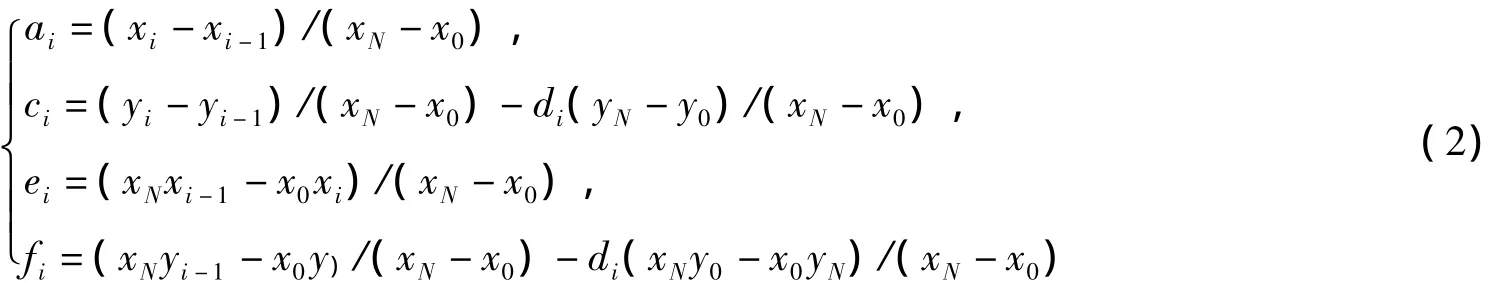
式中di(垂直比例因子)为自由变量，且di∈［0，1)，否则迭代函数系统不收敛.由式(2)可知，di的选取对于仿射变换其余四个参数的计算有着很重要的影响，故准确计算di对预测结果尤为重要.

1.2 垂直比例因子的算法

对于离散数据集，Mazel和Hayes提出了计算di的两种方法:几何法和解析法［5］.在几何法中，为了求得di，必须先求出分形插值曲线到数据集两端点所成直线的最大纵向距离的点，由于此点只是插值曲线上的点，未必是插值点，其位置通常难以确定.李国璋利用三次B－样条分形插值曲线，给出了求此点的代数解法［6］.然而此法在实用上很不方便，这里本文给出计算di的一种实用的方法.

根据分形插值函数的分数维定理，定义A为分形插值迭代函数系统的吸引子，如果，且插值点不共线，则A的分维数D满足:

式(3)只要验证复旦人民币汇率指数数据具有自相似性，就可以通过分维数D计算出di，而D与自相似理论中的关键性参数Hurst指数(H)有如下关系:D=2－H，所以通过准确估计H值来间接计算di是简便易行的.为了便于计算分析，设各个垂直比例因子di取值大小相等，均为|d|，则由式(3)可得:

根据式(4)，对复旦人民币汇率指数数据进行Hurst指数估计，进而求出di的值，再由式(2)确定出其它参数的值，构建出完整的迭代系统，从而得到预测曲线.这里定义分形插值曲线与原历史数据曲线的平均标准误差ε为

2 自相似性检测

描述一个自相似过程，关键的参数是Hurst指数，估计Hurst指数有方差－时间曲线法、R/S分析法(Rescaled Range Analysis)、周期图法、小波变换分析法等等.本文使用R/S分析法来估计Hurst指数，下面对R/S分析法进行简要描述，其他估算方法见文献［7］.R/S分析法是经典的Hurst指数估计算法，具体描述如下:

给定时间序列T(i)，i=1，2…，N，则

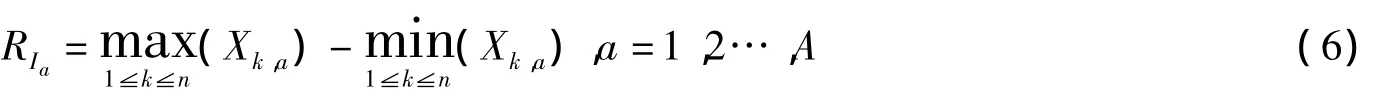
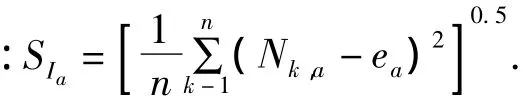
根据Hurst的发现，在分形布朗运动的情况下，当n充分大时，有(R/S)n∝cnH，式中H称为Hurst指数，且0≤H≤1.因此，我们只要对不同的n值，求出一系列的(R/S)n，然后利用log(R/S)n与log(n)的标绘图逼近，即

通过最小二乘法回归解出的斜率即为Hurst指数H.

3 实证分析

3.1 自相似性分析

选取时间跨度从2013年1月1日到2015年3月6日的复旦人民币实际有效汇率指数(按日发布)作为研究对象，共559个数据.为了消除时间序列可能存在的异方差，需要对数据进行必要的处理.利用公式Rt=ln Pt－ln Pt－1，其中Pt为第t日人民币汇率指数，Rt为第t日对数收益率，就将此时间序列分别转化为日对数收益率序列.图1给出了复旦人民币实际有效汇率指数和对数收益率的波动形态.

图1 复旦人民币汇率指数原始数据与对数收益率图

由图1可看出，收益序列呈现出剧烈波动和波动聚集效应等特征，呈非线性变化.为了刻画复旦人民币汇率指数的结构特征，使用R/S分析法和Hurst指数对其收益率序列进行分析，由公式(7)可估计出Hurst指数.绘制log(R/S)n关于log n的双对数图，如图2所示，其中直线的斜率就是Hurst指数的估计值H=0.6689.由于0＜H＜1，说明复旦人民币指数具有状态持续性，再由时间序列分维数D与Hurst指数H的关系可知，D=1.3311，表明该序列有分形统计自相似特征.

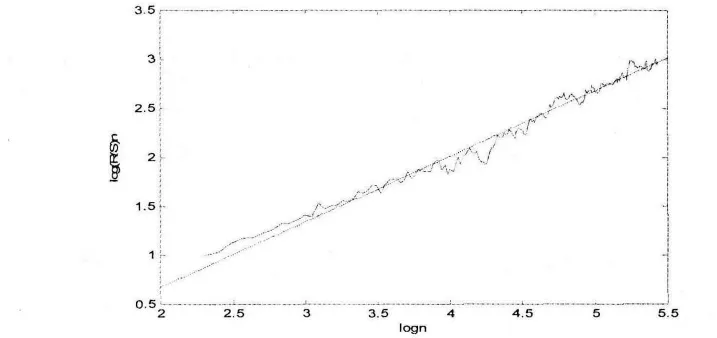
图2 复旦人民币指数收益率的R/S分析图

3.2 分形插值拟合与预测

选取时间跨度从2013年1月1日到2015年3月6日的复旦人民币实际有效汇率指数(按日发布)作为研究对象，共559个数据，原始数据图见图1.先对2013年1月1日到2015年1月23日的529个数据进行分形插值拟合.将这些数据按时间进行等距分割，使得xi=31i+1，i=0，1，…，18，取(xi，yi)，i =0，1…，18为插值点集，即为构造仿射分形插值函数所需的插值点.根据表达式(4)可求得垂直比例因子di=0.1420，再由式(3)确定迭代函数系的其他系数，这样就构造了一个含有18个仿射变换的迭代函数系.利用确定性迭代算法，经过三次迭代，得到如图3所示的分形插值拟合曲线.

图3 复旦人民币指数的分形插值拟合图

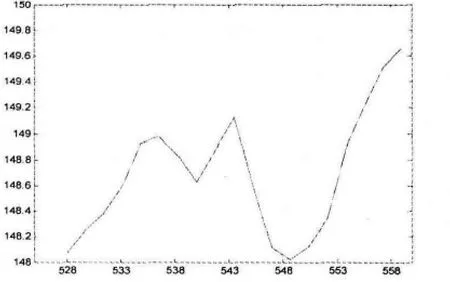
图4 复旦人民币指数的分形插值预测图

比较图1和图2发现，虽然在前529个数据的原始图与分形插值拟合图之间存在一些误差，但两者总体变化趋势是一致的.而且如果适当的增加插值点的个数或者增加迭代次数，将会更好的模拟原始数据图.这表明了利用分形插值来模拟复旦人民币指数波动形态是可行的.

下面利用分形插值外推法对复旦人民币汇率指数的变化趋势进行预测，选取从2015年1月23日到2015年3月6日的31个数据进行预测.设x19=31×19+1，根据汇率数据变化的统计自相似性和拟周期性，且由di=0.1420经验估计y19=149.66.再由式(1)和(2)确定了一个新的迭代函数系，经过三次迭代，得到复旦人民币指数在2015年1月23日到2015年3月6日这一段时间内的预测图，结果如图4所示.由图4可以发现，经过分形外推得到的预测数据与原始数据的基本走势是一致的，且平均相对误差约为2.618%.由此说明用分形插值来预测复旦人民币指数的走势是可行的.

4 结论

本文以复旦人民币实际有效汇率指数为研究对象，选取时间跨度从2013年1月1日到2015年3月6日期间的559个数据进行分析和预测.文中首先利用R/S分析法和Hurst指数分析复旦人民币指数收益率的结构特征，发现市场具有状态持续性和统计自相似性.再由分形插值函数的分数维定理，给出了计算di的一种简单实用的方法，并据此建立了能分析和预测复旦人民币指数的仿射分形插值模型.结果发现，基于分形插值模型对复旦人民币进行模拟和预测是可行的，而且结果与实际比较吻合.由于其平均标准误差仅为2.618%，可分析得出，利用Hurst指数来估计垂直比例因子是可行的，而且这种方法不仅有理论参考依据，而且也有较高的精度.同时，它给我们提供了一个定量分析计算垂直比例因子的方法，可为我们解决一些处理数据分析的工作时遇到的难题.

［1］陈学彬，王培康，庞燕敏.复旦人民币汇率指数的开发和应用研究［J］.复旦学报(社会科学版)，2011(2):1－15.

［2］黄飞雪，赵岩.基于分析的人民币外汇市场分形特征实证研究［J］.哈尔滨工业大学学报(社会科学版)，2008(6):6－71.

［3］Tang Xiaolei，Zhou Jizhong.Nonlinear relationship between the real exchange and economic fundamentals:Evidence from China and Korea［J］.Journal of International Money and Finance，2013(32):304－323.

［4］ZhaiMingyue.A newmethod for short－term load forecasting based on fractal interpretation and waveletanalysis［J］.Electrical Power and Energy Systems，2015(69):241－245.

［5］Mazel D S，Hayes M H.Using Iterated Function Systems to Model Discrete Sequences［J］.IEEE Transactions on Signal Processing，1999，40(7):1724－1734.

［6］李国璋，黄建波，黄海英.基于B－样条分形插值的垂直尺度因子的计算方法［J］.军械工程学院学报，2006，18(2):76－78.

［7］Zhai Mingyue.Signal recovery in power line communications systems based on the fractals［J］.IEEE Transactions Power Delivery，2011，26(3):1864－1872.

Forecasting Analysis of the Fudan RMB Exchange Rate Indices Based on Fractals

KANG Feng－hua
(School of Applied Mathematics，Nanjing University of Finance and Economics，Nanjing，210023，China)

The structural feature of the Fudan RMB exchange rate indices is investigated by using R/Sanalysis and Hurst indices in this paper.We find out that Fudan RMB exchange rate indices have the persistence of state and statistical properties of fractal distribution.We study the changing law of the Fudan RMB exchange rate indices during a certain time by establishing fractal interpolation model，and predict the changing tendency of the indices in a short time.We point out the forecasting results are almost the same as the original datamovements，and the standard error is only 2.618%.The fact shows that using Hurst indices and fractal interpolation model to calculate the vertical scale factor and predict the Fudan RMB exchange rate indices is feasible.

fractal interpolation;R/S analysis;Hurst indices

F832.52

A

1672－2590(2015)03－0065－05

2015－03－18

教育部人文社科规划基金项目(12YJAZH020);南京财经大学研究生创新课题

康凤华(1989－)，女，河南驻马店人，南京财经大学应用数学学院硕士研究生.