非对称矩阵值函数的连续性和微分性

陈 涛，田 力

(泰山学院数学与统计学院，山东泰安 271021)

非对称矩阵值函数的连续性和微分性

陈 涛，田 力

(泰山学院数学与统计学院，山东泰安 271021)

非对称矩阵值函数的性质在研究其最优化问题时起着非常重要的作用.本文在非对称矩阵值函数定义的基础上，基于对称矩阵值函数与非对称矩阵值函数之间的关系，给出了非对称矩阵函数的一种新的连续性和微分性.

奇异值分解;非对称矩阵值函数;连续性;可微性

1 预备知识

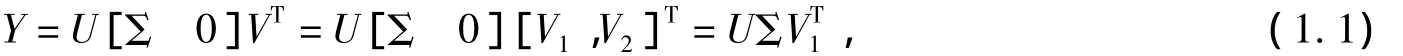
定义1.1［1］设g∶→是一实值函数，非对称矩阵值函数G∶p×q→p×q为

这里g(Σ)=diag［g(σ1)，…，g(σp)］.

定义1.2［1］设线性算子Ξ∶p×q→Sp+q，其中

引理1.1［2］令g∶→，g(0)=0是实值函数，Y∈p×q具有(1.1)的奇异值分解.则有(1.2)给出的相应的非对称的矩阵值函数G(Y)有定义.

这里给出的U，V1，V2如同(1.1)，Ξ(Y)具有下面的特征值分解

因为Ξ(Y)是对称的，和f=g有关的F(Ξ(Y))是有定义的.

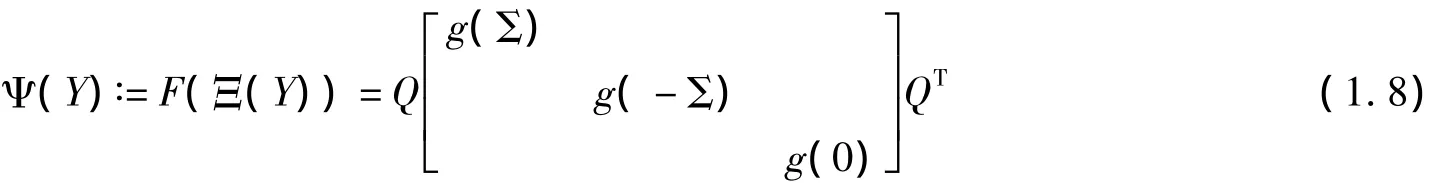
则由(1.6)，(1.7)和(1.8)，可以得到

联系(1.4)可以推出

即上述非对称的矩阵值函数G(Y)有定义，由于UV1依赖于Y的奇异值分解，由(1.3)可知g(0)= 0是G有定义的充分必要条件.这样对定义在+上的实值函数g，本文总是假设g(0)=0.

2 主要结论

下面讨论由(1.2)定义的非对称矩阵值函数G的连续性及可微性.

令Sn是实对称矩阵空间，对任意的X∈Sn，定义X的正交向量集

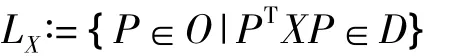
这里O表示n×n正交矩阵空间，D表示n×n对角元素非增的对称矩阵空间.

引理2.1 对任意的X∈Sn，存在数η＞0和ε＞0，使得

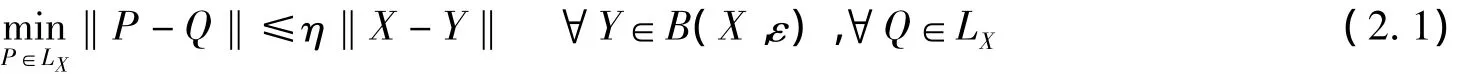
引理2.2 对任意的X，Y∈Sn，令λ1，λ2，…，λn和μ1，μ2，…，μn分别是X和Y的特佂值，则

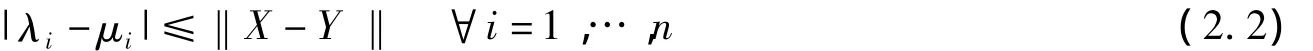
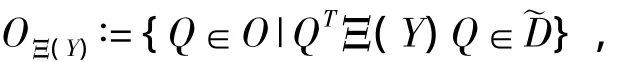
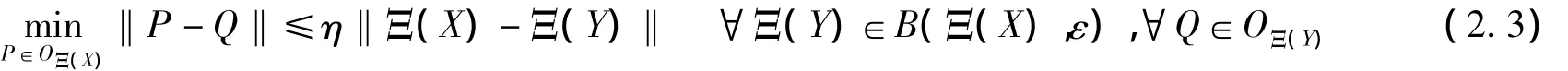
证明:对任意P∈LΞ(X)和Q∈LΞ(Y)存在一个置换矩阵W，使得WP∈OΞ(X)，WP∈Ξ(Y)，则有引理2.1，存在数值η＞0和ε＞0，使得

证明:(1)由(1.9)知，G在Y连续当且仅当Ψ在Y连续.首先证明若g在σ1，σ2，…，σp连续，Ψ在Y连续.

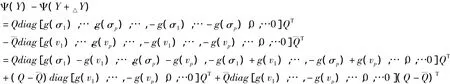
→0当△Y→0时.

这表明G在Y连续.

假设G在Y连续，对任意正交矩阵U和V，使得Y=U［Σ 0］VT，这里Σ=diag［σ1，…，σp］，则对任意的i∈{1，…，p}，当μi→σi时，

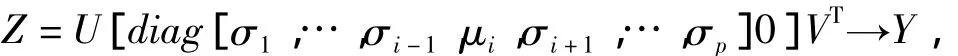
从而G(Z)→G(Y)，由G的定义，g(μi)→g(σi)，也就是说，g在σi处连续.

(2)是(1)的直接结果.

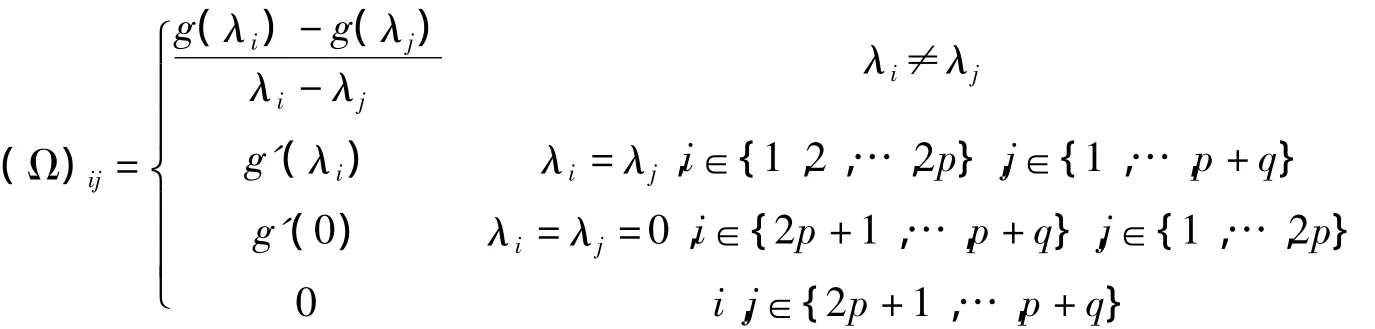
的(p+q)×(p+q)的对称矩阵.

定理2.3 Ψ在Y可微的充要条件是g在σ1，σ2，…，σp可微，并且，若Ψ在Y可微，则有

证明:假设g在σ1，σ2，…，σp可微，则g在－σ1，－σ2，…，－σp可微，也就是说g在λ1，λ2，…，λ2p可微.

由定理2.1存在数值η＞0和ε＞0，使得

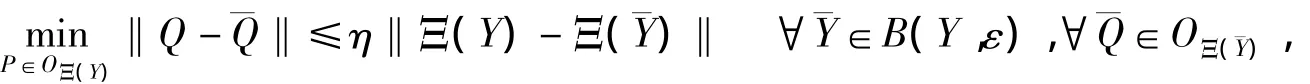
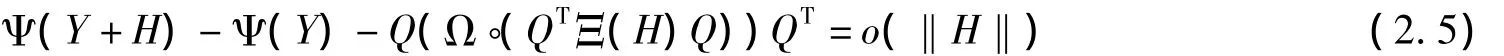
连同Q的第三条性质，有Ψ在Y可微，并且Ψ'(Y)由(2.4)给出.

令v1，v2，…，vp+q是Ξ(Y+H)的特征值:τ1，τ2，…，τp是Y+H的奇异值，任意取定¯Q∈OΞ(Y+H)，则

由定理2.1存在Q∈OΞ(Y)，满足

为简单起见，令r表示(2.5)的左端，即，

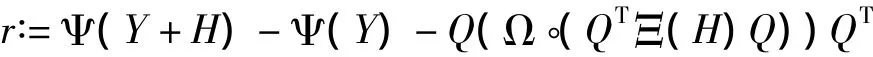
这里

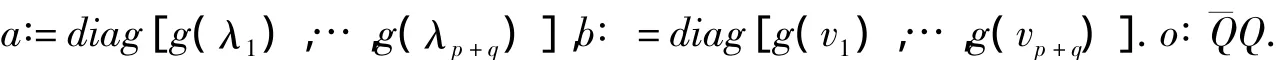
注意到，

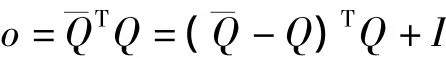
联合(2.13)有

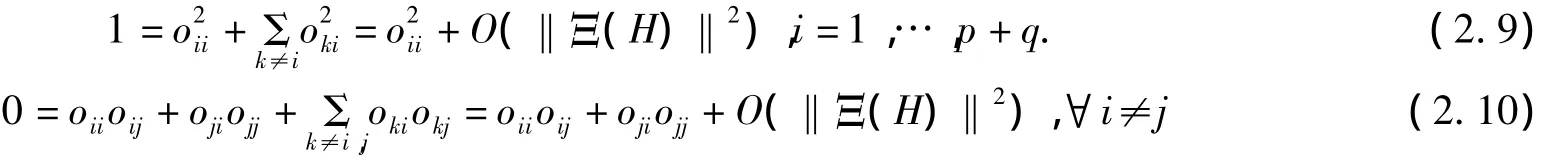
又因为

所以

对任意的i∈{1，…，2p}，由(2.7)、(2.11)及g(vk)=g(0)=0，k≥2p+1，我们有

因为g在λ1，λ2，…，λ2p可微，

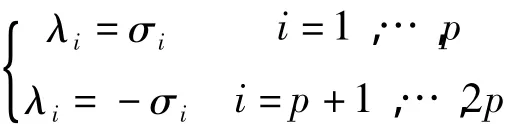
由引理2.1右式即o(‖Ξ(H)‖).

对i∈{2p+1，…，p+q}，因为k≠i，我们有

对任意的i，j∈{1，…，p+q}，i≠j，由(2.7)、(2.11)和g(vk)=g(0)=0，k≥2p+1，我们有

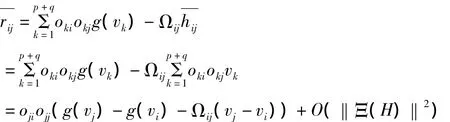
显然r=o(‖H‖).因此，得到

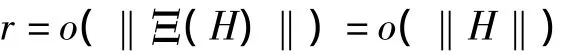
这表明Ψ在Y可微，并且Ψ'(Y)由(2.11)给出.

由2.1若σp=0，则g在0是可微的.F在Ξ(Y)是可微的，则由复合函数求导的链式法则Ψ在Y可微，并且

虽然当i，j∈{2p+1，…，p+q}，Ωij=g'(0)可能不为0，(Ξ(H))ij=0，(2.12)和(2.4)是一致的.

［1］张贤达.矩阵分析与应用［M］.北京:清华大学出版社，2004.

［2］张宁.矩阵值函数的微分与应用［D］.大连:大连理工大学，2013.

The Continuity and Differentiability of Non－symmetric Matrix Valued Function

CHEN Tao，TIAN Li
(School of Mathematics and Statistics，Taishan University，Tai＇an，271021，China)

The properties of the non－symmetric matrix valued function play a very important role in the study of the optimization problems.In this paperwe offer the definition of non－symmetricmatrix valued function firstly，and then give some new properties on the continuity and differentiability of non－symmetricmatrix valued function based on the relationship between the symmetric matrix valued functions and non－symmetric matrix valued functions.

singular value decomposition;non－symmetricmatrix valued function;continuity;differentiability

O177.1

A

1672－2590(2015)03－0001－05

2015－04－08

陈 涛(1971－)，男，山东泰安人，泰山学院数学与统计学院副教授.