一种高误码（n，k，m）非系统卷积码盲识别算法＊

张 岱 张 玉 杨晓静

（1.电子工程学院504教研室，合肥，230037；2.电子工程学院402教研室，合肥，230037）

引 言

在数字通信中，信道编码可以提高通信的可靠性，目前信道编码主要包括线性分组码、卷积码、Tur-bo码和LDPC码等［1-2］。其中，Viterbi译码算法的提出和不断改进［3］，降低了卷积码编译的复杂度，使其广泛应用在卫星通信、深空探测等领域。因此卷积码盲识别研究在信息截获领域，智能通信领域以及非合作信号处理领域有着重要的意义［4-5］。

卷积码盲识别技术受到了国内外越来越多研究人员的关注［5］，目前的识别方法主要有基于改进欧几里德算法［6］、Walsh-Hadamard分析法［7］、基于BM的快速合冲法［8］、基于对偶码代数特性的循环识别方法［9-10］和基于矩阵分析的识别方法［11］等。其中改进欧几里德算法只适用于1／n码率卷积码，具有使用数据量小的优点，但不具有容错性；Walsh-Hadamard分析法同样只适用于1／n码率卷积码，具有较好的容错性，但该方法必须预估卷积码的码率和码字起点，即需要一定的先验条件，且使用的数据量巨大；基于BM的快速合冲法使用较小数据量便能达到识别效果，但该方法只适用于1／2码率的卷积码；基于对偶码代数特性的循环识别方法可对（n，k，m）卷积码进行识别，该方法至少需使用数万比特码字数据进行识别，在误码率为0.02时，可达到50%以上的识别率，具有一定的容错性，但需要码字起点等先验条件；基于矩阵分析求解校验序列的识别方法可利用少量的数据对（n，k，m）卷积码进行全盲识别，但当误码率超过0.01时，容错性能将急剧下降。同时，以上两种识别方法均未对非系统卷积码的生成矩阵进行识别。

综上所述，现有的卷积码识别方法主要针对（n，1，m）卷积码及（n，k，m）系统卷积码进行识别，且需要一定的先验信息，对性能更优的（n，k，m）非系统卷积码进行有效识别的方法尚未见诸报道。本文所提出的方法可在不需要任何先验条件及高误码环境下，实现对（n，k，m）非系统卷积码的识别，该识别方法创新性的工作主要表现为：（1）通过建立一个可变的数据矩阵模型进行数据预处理，筛除了线性约束关系较差的码字，提高了数据利用率和识别的容错性能；（2）改进了卷积码参数识别中编码记忆长度的识别方法，通过统计筛选，提高了卷积码参数的识别精度。同时，提出了生成多项式矩阵组的概念，为非系统卷积码生成多项式矩阵的识别创造条件；（3）通过对非系统卷积码生成多项式矩阵的特性进行分析，提出了基于阶次分析的非系统卷积码生成多项式矩阵识别步骤。

1 （n，k，m）非系统卷积码识别问题描述

当前实际应用的卷积码均是二进制卷积码，即建立在二元域F2上。通常情况下，卷积码的参数可表示为（n，k，m），称k为信息位长度，n为码字长度，m为编码记忆长度。

记u和c分别为（n，k，m）卷积码的信息序列和码字序列，在环F2［x］上，二者满足关系如下

式中：G（x）为（n，k，m）卷积码的生成多项式矩阵。卷积码是线性的，因此也像分组码一样存在校验多项式矩阵，并满足以下关系

式中：G（x）为k×n阶多项式矩阵；H（x）为 （n-k）×n阶多项式矩阵。则由式（1）和式（2）可得

通过式（3），可以完成对卷积码校验矩阵的识别［4］。然而与系统卷积码不同，对于（n，k，m）非系统卷积码的校验多项式矩阵H（x），存在多个G（x）与之满足式（2）中关系，且非系统卷积码的生成多项式矩阵与校验多项式矩阵之间并无严格的相似转换关系，因此当通过式（2）求解得到一系列生成多项式矩阵时，需要对其进行筛选以得到原卷积码的生成多项式矩阵，以完成最终识别。经过上述分析，（n，k，m）非系统卷积码的识别可分为以下两个部分：（1）卷积码参数（码长n，码率k／n，记忆长度m）的识别。（2）求解卷积码生成多项式矩阵组，并最终识别出原卷积码的生成多项式矩阵。

根据以上内容，本文解决（n，k，m）非系统卷积码的盲识别问题主要分为以下3步：

（1）建立可变的数据矩阵模型，利用卷积码码字间的线性相关性，对侦收到的卷积码数据进行预处理；

（2）选取预处理后的卷积码数据矩阵，对其进行综合统计分析，识别出码率k／n、估计记忆长度，并利用校验序列求解生成多项式矩阵组；

（3）设定卷积码生成多项式矩阵筛选规则，利用阶次分析对生成多项式矩阵组进行筛选，并作初等变换处理，最终识别出原卷积码的生成多项式矩阵G（x）。

2 对高误码（n，k，m）非系统卷积码的盲识别算法

2.1 卷积码数据预处理

针对目前卷积码识别容错性不高的问题，本文提出了一种基于卷积码码字间线性相关性的方法，对侦收的卷积码码字进行预处理，筛取具有较好线性相关性的码字，大大减小了误码对识别算法的影响。同时，由于在不同环境下，所侦收的码字数据量差异很大，为提高在不同应用背景下的侦收数据利用率，本文提出建立一个可变数据矩阵模型的方法，提高了侦收数据利用率，使对所侦收编码数据的利用更为灵活。

设c为（n，k，m）卷积码的码字序列，在F2上表示如下

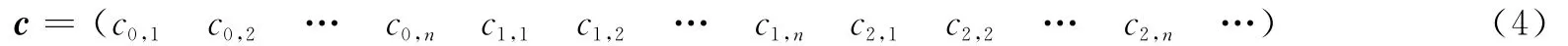
将该（n，k，m）卷积码的校验矩阵表示为

由c·HT＝0，可知编码输出的码元必然满足一定的约束关系。从H的结构可知，每次c都有最多N＝n（m＋1）个元素与HT相乘。也就是说从码字分组起点开始取N个c中的子码，那么这N个相邻子码都符合方程x1c1＋x2c2＋…xNcN＝0，其中xi由H决定。x·c＝0称为编码约束方程，N为编码约束长度。

定义1［11］设h′为F2上半无限长行向量，对于卷积码码字序列c，若满足C·h′T＝0，则称h′为（n，k，m）卷积码的校验序列。

由定义1，校验矩阵H的各行Hi均为校验序列，其与码字间的线性关系可表示为

由以上分析，相邻的N个卷积码码字间具有固定的线性约束关系。对此，将侦收的大量待识别比特流数据B＝（b0，b1，b2，…）逐行注入到x行y列的多个数据矩阵模型D中，其中y要大于编码约束长度N，设定x＝y＋1。实际应用中，卷积码的复杂度决定了记忆长度m和码长n不会太大，一般有m≤7，2≤n≤6，所以y取48即可。当侦收数据量较大时，可将卷积码数据不重复地注入到矩阵模型中，当侦收数据量有限时，对数据矩阵模型进行如下设置：

第1个数据矩阵D1：第1行以ba为起点，取连续长为L比特的数据；第2行以ba＋d为起点，取连续长为L比特的数据；其他行的设置依此类推，最终将数据注满该数据矩阵。其中d设置为码长的整数倍，以保留各列数据间的线性关系（一般取4，5，6进行逐个循环）。

第2个数据矩阵D2：码字起点可设为ba＋p，其中p≥1为一自由整数变量，这样根据总体数据量大小调整p的值，可完成对侦收数据的灵活利用，以达到更好的识别效果。其他数据矩阵模型设置依此类推，最终完成所有数据的注入。

按上述规则，第q个数据矩阵模型Dq表示如下

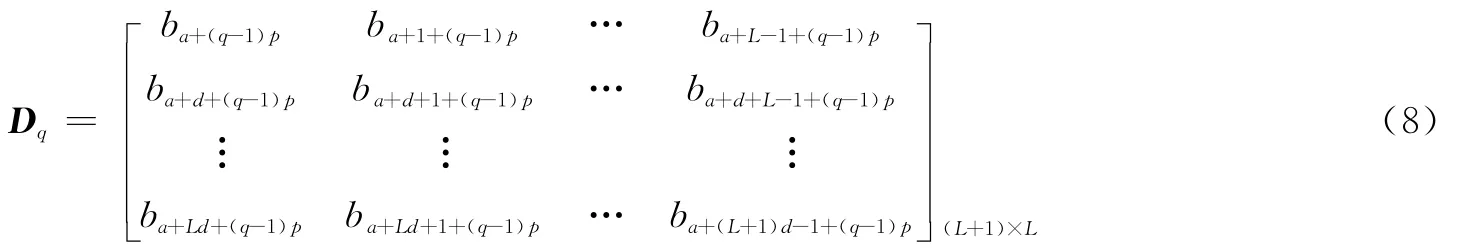
当将待识别卷积码比特流注入到数据矩阵模型之后，矩阵秩的大小表征了该数据矩阵内数据的线性约束关系，矩阵秩越小，码字间的线性约束关系越强。对此，计算各个数据矩阵模型的秩rank（Di），根据各个矩阵秩的大小对所有数据矩阵按秩由小到大的顺序进行排序。

由于数据矩阵的起始码字与卷积码码组的起始码字并不严格对应，因此，即使是线性关系完备的数据矩阵，其秩的值也并不一定达到最小［12］。针对以上情况，对数据矩阵的秩设判决门限λ，由于一般（n，k，m）卷积码的码长范围为2≤n≤6，对λ设置如下

根据矩阵秩判决门限，设置卷积码数据矩阵的筛选准则如下

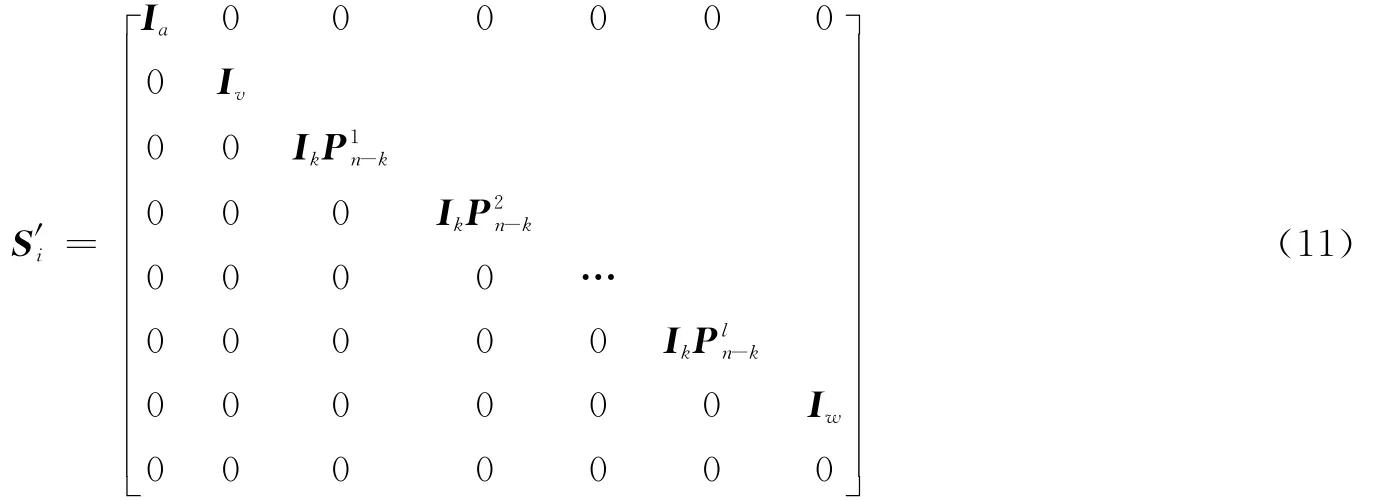
将卷积码数据矩阵组按式（10）进行筛选后，选择符合线性约束关系的前r个数据矩阵（r的大小视信道干扰情况而定），并分别赋值给 （L＋1）×L阶矩阵S1，S2，…，Sr，最终得到一个F2上的二维矩阵序列S＝（S1S2…Sr），将预处理后数据保存，以待下一步处理。

2.2 卷积码参数识别及生成多项式矩阵组的求解

逐个选取2.1节中得到的矩阵序列S中的矩阵Si（1≤i≤r），并进行初等行变换处理，可化简为下面矩阵［4］

侦收码字序列中存在的码字错误往往为突发错误，在经预处理后，得到的码字数据矩阵中误码较少，进行初等变换之后将仅造成校验位发生错误，而不会改变码字整体的线性约束关系。通过对一系列数据矩阵Si（1≤i≤r）逐个进行上述分析，统计不同数据矩阵识别后的参数ni，ki，若ni共有b种取值，记为n′1，…，n′b，则分别计算其出现概率p（n′j）（1≤j≤b）。最终识别出（n，k，m）卷积码的码长n为

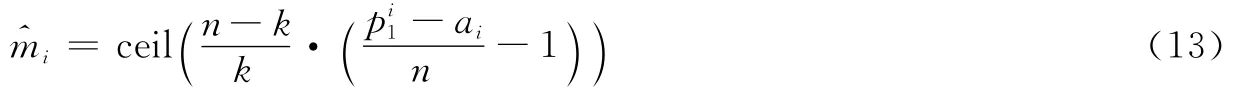
式中：ceil（）表示向上取整。由于码字中出现误码将会破坏码字间的线性约束关系，使其约束长度增大或不再存在线性约束关系，对得到的不同估计值，筛选出所有估计记忆长度中的最小值，最终得到该（n，k，m）卷积码的估计记忆长度。从矩阵序列S′中选取与参数对应的数据矩阵，组成矩阵序列S″并保存，即完成了卷积码参数的识别，并进一步进行了卷积码码字数据筛选。S″记为

在得到经进一步筛选的卷积码码字数据之后，根据文献［11］中基于校验序列的（n，k，m）卷积码识别方法，对原卷积码的生成多项式矩阵组进行识别。对于式（14）中的l个数据矩阵，分别抽取其前r个校验序列，记为

式中：代表矩阵中的首列的设置依此类推。

定义2 如果两个生成多项式矩阵G（x）和G′（x）可编码生成同一个卷积码，那么它们就是等价的，等价生成多项式矩阵的集合称为生成多项式矩阵组。

不考虑恶性码及编码器缺失等情况，对于（n，k，m）非系统卷积码的校验矩阵H，存在多个非零矩阵Gi满足Gi·HT＝0（i＝1，2，…），则Gi均可为该卷积码的生成矩阵［1］。由定义1中校验序列的概念可得，对于式（16）中多个校验序列构造的多项式矩阵H′j（x），必有

则由H′求解出生成多项式矩阵组的具体步骤如下：

（1）取H′1，对其中的r个校验序列分别按码长n抽取，由此将（1≤i≤r）构造成F2（x）上的n个多项式（x），…，（x），等效于校验多项式矩阵H（x）的某一行，记作hi（x）。

（2）由识别出的参数码长n、信息位数k和估计记忆长度假设生成多项式矩阵G（x），G（x）的k行分别记为gj（x），1≤j≤k。由式（2）建立k个gj（x）与r个hi（x）的线性方程组，gj（x）·［hi（x）］T＝0，当j＝1时，有

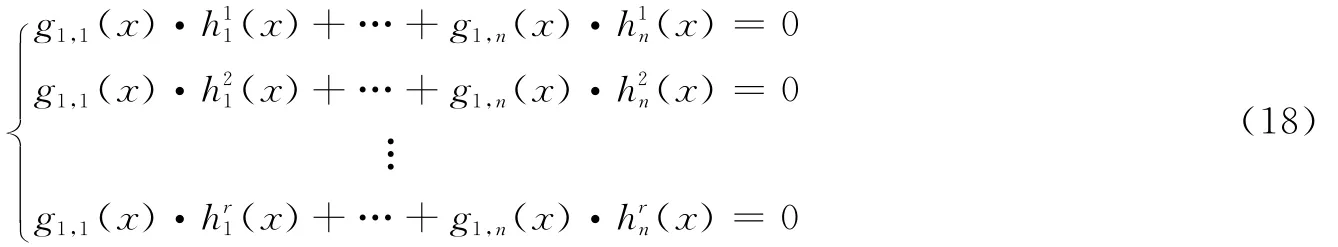
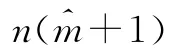
（3）将方程组（18）转化成F2（x）上的方程组，易知其解空间的维数为k，通过行阶梯法求解得到一系列以生成多项式矩阵行向量为基的解向量，取前k个解序列，记为

（4）依照步骤（1），（2），（3）对H′中的其他校验序列矩阵进行处理，最终得到生成多项式矩阵组

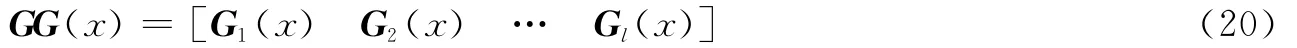
2.3 生成多项式矩阵的识别

由定义2可知，对于非系统卷积码，可存在多个生成矩阵与其校验矩阵相对应，然而，不同的卷积码生成矩阵在性能上存在着巨大差异。

定义3 对于卷积码的生成多项式矩阵G（x），定义其逆为G-1（x），满足

如果G-1（x）可实现，从传输函数的角度来考虑，则它相当于卷积码的译码器，在接收端应有

假设有一个卷积码的G（x）＝［1＋x，1＋x＋x2］，可求得G-1（x）＝［x，1］T，可以看出此译码器中仅有一级延时存储单元，故在译码过程中码字中的错误只要经一个单位时间即被遗忘掉，称这种G-1（x）为前馈逆。假设另一个G（x）＝［1＋x，1＋x2］，则有

式中：G-1（x）分母为1＋x，在电路上相当于作除法，称为反馈逆。这种电路的记忆是无限的，因为1／（1＋x）＝1＋x＋x2＋…，所以错误无法消除。这个例子里误码会无限传播，称之为Ι类无限误差传播，这个码便称为恶性码［13］。只要G-1（x）是无时延的有限多项式，其所代表的码就不会是恶性的。

定理1 如果一个卷积码的G（x）和G-1（x）都是有限多项式矩阵，则G（x）就是该卷积码的一个基本编码矩阵［13］。

而对于有限域上的多项式矩阵G（x），计算G-1（x）的过程较为复杂，因此将定理1作为筛选卷积码生成多项式矩阵的依据会造成巨大的计算量，不易实现。做出如下改进。

推论1 对于（n，k，m）卷积码，其生成多项式矩阵G（x）表示如下

则G（x）为基本编码矩阵的必要条件是

证明：

若gcd（gi，1（x），gi，2（x），…，gi，n（x））＝gi（x）i＝1，2，…，k，并满足

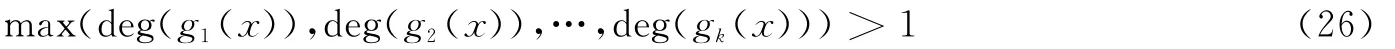
则有

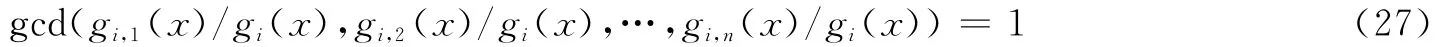
由有限域上多项式的性质可知，必存在hi，1（x），hi，2（x），…，hi，n（x）使得［14］

结合式（21）可得

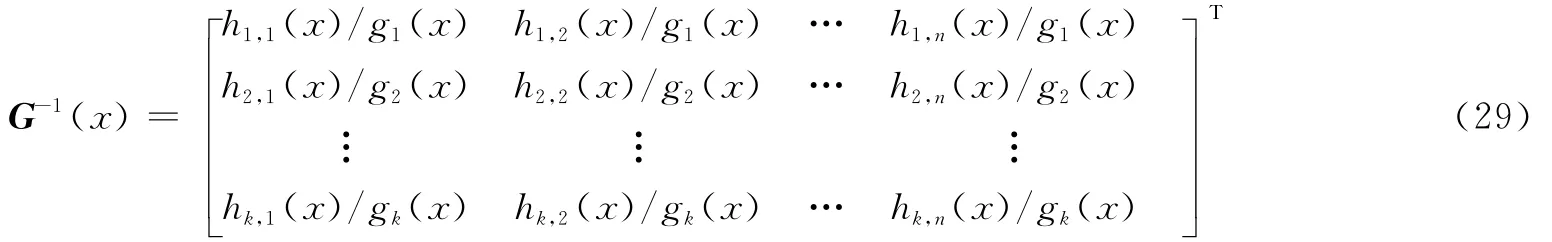
由式（29）可知，G-1（x）存在反馈逆，则由G（x）生成的卷积码为恶性码。由以上步骤反证得到若G（x）生成的卷积码为非恶性码，则必有式（25）成立，从而推论1得证。根据上述定义和推论，对（n，k，m）非系统卷积码生成多项式矩阵的识别步骤如下：

（1）对2.2节中所得到的生成多项式矩阵组GG（x），设置累积量记录其中不同的元素多项式矩阵出现次数，将不同的多项式矩阵按其累积量由大到小的顺序重新排序如下

（2）对G′p（x）的各行求其最大公因式，若阶次不为1，则将该生成多项式矩阵舍弃。

（3）将G′p（x）按列表示如下

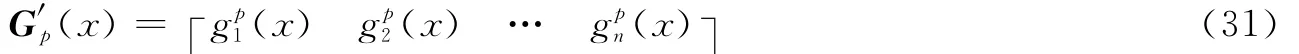
若有（x）＝0，1≤j≤n，即输出码字中某一路存在缺失，则将该生成多项式矩阵舍弃，取G′p＋1（x）返回步骤（2）继续执行。

（4）对于满足步骤（2），（3）中条件的生成多项式矩阵G′p（x），将其按行表示如下

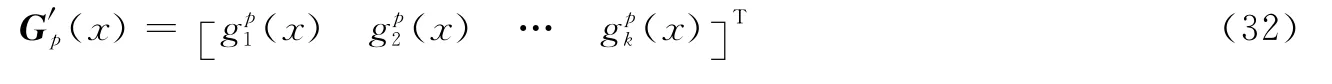
记G′p（x）的阶次如下

若对G′p（x）进行初等行变换后，使得deg（G′p（x））降低，则保留其初等行变换后的形式并替代原G′p（x），否则仍保存原G′p（x）。则G′p（x）即为最终识别得到的原（n，k，m）非系统卷积码的生成多项式矩阵，由G′p（x）的行阶次最终确认记忆长度m为

3 实例仿真分析

首先对所提出识别算法进行仿真验证，随后使用蒙特卡罗法，将本文算法与其他算法在卷积码参数识别性能上作对比，最后对采用不同数据量时对非系统卷积码的识别效果进行比较。

3.1 算法验证

以常用的（3，2，4）非系统卷积码为例验证本文算法的可行性。（3，2，4）非系统卷积码的生成矩阵用八进制表示为G＝（23 35 0；0 5 13），则其生成多项式矩阵为

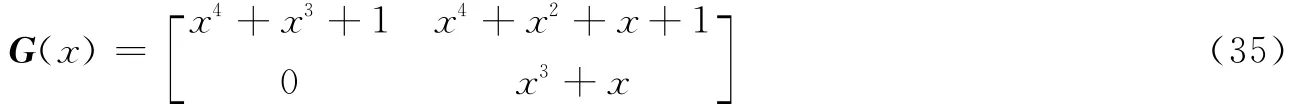
选取5 000bit误码率为2%的（3，2，4）卷积码数据进行仿真如下。首先，将得到的卷积码数据逐行注入2.1节中建立的数据矩阵模型中，由于所侦收的数据量有限，设置可变矩阵参数p＝5，通过数据预处理，从预处理后的数据矩阵组中选取一个数据矩阵，使用2.2节中的方法对其进行卷积码参数识别，得到式（11）形式的分析矩阵如图1所示。

对图中矩阵分析可得，n＝3，k＝2，p＝24，a＝1，由记忆长度估计式（13）计算得

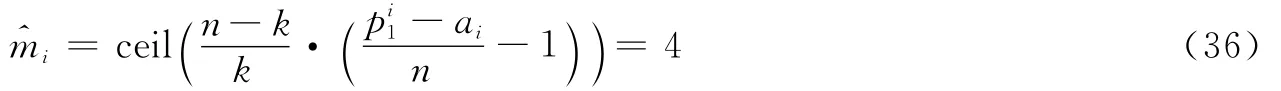
使用2.2节中方法进行统计，最终得到该卷积码的参数为码长n＝3，信息位长度k＝2，估计记忆长度＝4。接下来求解该卷积码的生成多项式矩阵组，使用2.3节中的步骤（1），按累积量进行排序后，得到生成多项式矩阵组如下

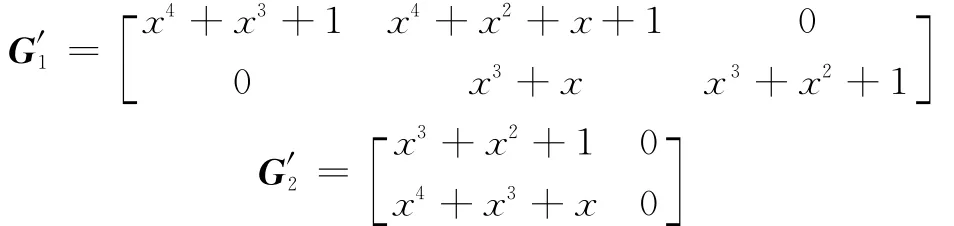
图1 数据矩阵模型化简结果Fig.1 Results of simplifying data matrix model

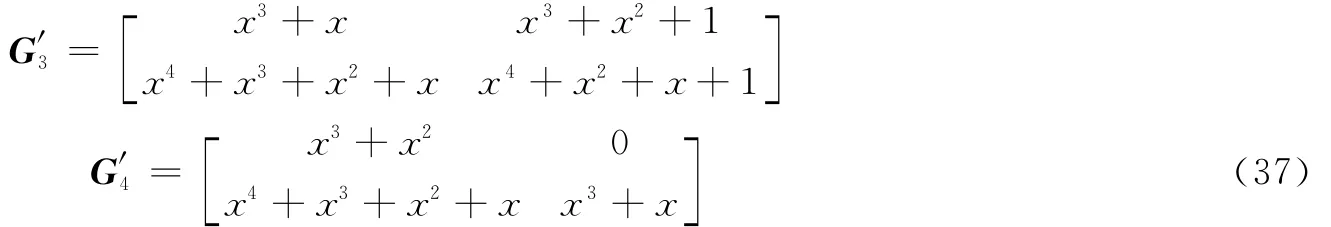
对矩阵组（37）执行2.3节中的非系统卷积码生成多项式矩阵识别步骤，最终识别出原卷积码的生成多项式矩阵为

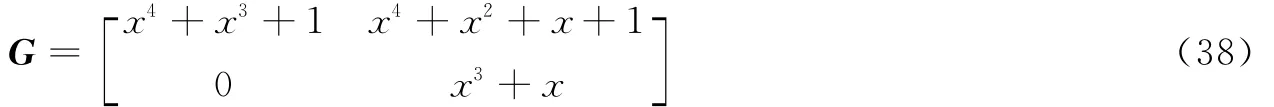
与式（35）相同，同时确认记忆长度m＝4，达到了识别目的。对以上例子中得到的生成多项式矩阵组进行分析可得，即使误码率变化，导致按累积量排序后生成多项式矩阵组中元素的顺序发生改变，利用2.3节中的非系统卷积码生成多项式矩阵的识别步骤仍可准确识别，这表明了本文所提出算法的可行性。

3.2 识别性能对比

由于（n，k，m）非系统卷积码的参数识别和（n，k，m）系统卷积码的参数识别具有通用性，现将本文识别算法与文献［10-11］中卷积码识别算法在参数识别上的性能进行比较，采用20 000bit（3，2，4）非系统卷积码数据进行参数识别时，其识别性能对比如图2所示。

由图2可以看出，当误码率达到0.02时，文献［11］所提出的矩阵分析方法识别率下降到50%以下，文献［10］中基于对偶码代数特性识别方法的识别率在65%左右，而本文算法的识别率仍高于80%。综上可知，本文所提出的（n，k，m）非系统卷积码盲识别算法在卷积码参数识别上与矩阵分析法和基于对偶码代数特性识别方法相比，在误码适应能力上具有优势。同时，由于本文算法在识别过程中进行了预处理和逐层数据筛选的过程，将线性关系缺失的码字不断筛除，减少了矩阵分析的数据量，从而在计算量上也低于另外两种（n，k，m）卷积码识别方法。

此外，本文所提出的（n，k，m）非系统卷积码盲识别算法在应用上还具有较强的灵活性，这集中体现在2.1节中可变数据矩阵模型的建立上，可根据侦收数据量的不同进行模型上的调整。现以（3，2，4）卷积码和（5，1，6）卷积码为例，分别选取500，2 000，5 000，10 000bit侦收编码数据，设置不同误码率进行全盲识别，通过蒙特卡洛仿真实验统计对应的识别成功概率（包括非系统卷积码参数和其生成多项式矩阵），如图3所示。

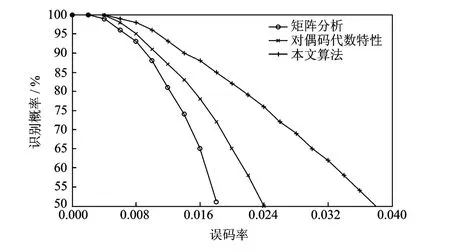
图2 不同误码环境下识别概率对比Fig.2 Recognition probility in different bit error rates

由图3的统计结果可知，本文算法可对不同量级数据量的非系统卷积码进行全盲识别，且随着侦收数据量的提高，算法容错性能逐渐增强，其中，在取得10 000bit侦收数据的情况下，当误码率达到0.03时，对（3，2，4）卷积码仍具有接近70%的成功识别率，对（5，1，6）卷积码具有接近60%的识别率。从理论上来看，由于本文算法采用了逐层筛选的方法，不断提取侦收数据中线性约束关系完备的码字，当侦收数据量非常巨大时，该方法对高误码的卷积码数据将取得十分理想的识别效果。

同时，通过两种卷积码的识别结果对比，可以看出，随着编码约束长度的增加，识别难度逐渐增大。这是由于编码约束长度较大时，编码数据线性相关性更容易被错误码字破坏的缘故。

图3 不同侦收编码数据量对应的识别概率Fig.3 Recognition probility of different received coded data sizes

4 结束语

本文提出了一种高误码（n，k，m）非系统卷积码盲识别算法，通过建立可变的数据矩阵模型对侦收数据进行预处理，较以往卷积码识别方法具有数据利用灵活、利用率高的特点。同时改进了矩阵分析法中对卷积码参数的识别方法，通过统计分析，提高了卷积码参数的识别精度，在求解出生成多项式矩阵组之后，通过对非系统卷积码的生成多项式矩阵特性进行分析，提出了非系统卷积码生成多项式矩阵的筛选条件，最终完成了对（n，k，m）非系统卷积码的识别。本文识别方法不需要任何先验条件，数据利用率高并具有较好的容错性，在误码率为0.02的条件下，对（3，2，4）非系统卷积码的正确识别率达到80%以上，弥补了当前卷积码识别研究上的不足，在智能通信及信息截获等领域具有重要应用意义。

［1］ 刘玉君.信道编码［M］.郑州：河南科学技术出版社，2001：45-47，190-216.

Liu Yujun.Channel coding［M］.Zhengzhou：Henan Publishing House of Science＆Technology，2001：45-47，190-216.

［2］ 张艳，仰帆枫.基于非规则LDPC码的协作 MIMO系统性能分析［J］.数据采集与处理，2013，28（6）：714-718.

Zhang Yan，Yang Fanfeng.Based on irregular LDPC cooperative MIMO system performance analysis［J］.Journal of Data Acquisition and Processing，2013，28（6）：714-718.

［3］ Zhou Ting，Xu Ming，Chen Dongxia，et al.Constrained Viterbi algorithm and its application to error resilient transmission of spirit coded images［J］.Transactions of Nanjing University of Aeronautics＆Astronautics，2008，25（2）：155-159.

［4］ 张永光，楼才义.信道编码及其识别分析［M］.北京：电子工业出版社，2010：9-94.

Zhang Yongguang，Lou Caiyi.Channel coding recognition and analysis［M］.Beijing：Publishing House of Electronics Industry，2010：9-94.

［5］ 解辉，黄知涛，王丰华.信道编码盲识别技术研究进展［J］.电子学报，2013，41（6）：1166-1176.

Xie Hui，Huang Zhitao，Wang Fenghua.Research progress of blind recognition of channel coding［J］.Acta Electronic Sinica，2013，41（6）：1166-1176.

［6］ 刘建成，杨晓静，张玉.基于改进欧几里德算法的（n，1，m）卷积码识别［J］.探测与控制学报，2012，34（1）：64-68.

Liu Jiancheng，Yang Xiaojing，Zhang Yu.Recognition of（n，1，m）convolutional code based on improved Euclidean algorithm［J］.Journal of Detection＆Control，2012，34（1）：64-68.

［7］ 刘健，王晓君，周希元.基于 Walsh-Hadamard变换的卷积码盲识别［J］.电子与信息学报，2010，32（4）：884-888.

Liu Jian，Wang Xiaojun，Zhou Xiyuan.Blind recognition of convolutional coding based on Walsh-Hadamard transform［J］.Journal of Electronic＆Information Technology，2010，32（4）：884-888.

［8］ 邹艳，陆佩忠.关键方程的新推广［J］.计算机学报，2006，29（5）：712-718.

Zou Yan，Lu Peizhong.A new generalization of key equation［J］.Chinese Journal of Computers，2006，29（5）：712-718.

［9］ Marazin M，Gautier R，Burel G.Dual code method for blind identification of convolutional encoder for cognitive radio receiver design［C］／／GLOBECOM Workshops 2009.Rennes，France：IEEE Press，2009：1-6.

［10］Marazin M，Gautier R，Burel G.Blind recovery of k／n rate convolutional encoders in a noisy environment［J］.Wireless Comunications and Networking，2011，2011（1）：1186-1687.

［11］杨晓静，刘建成，张玉.基于求解校验序列的（n，k，m）卷积码盲识别［J］.宇航学报，2013，34（04）：568-573.

Yang Xiaojing，Liu Jiancheng，Zhang Yu.Blind recognition of（n，k，m）convolutional codes based on solving check-sequence［J］.Journal of Astronautics，2013，34（04）：568-573.

［12］田同旺.卷积码识别技术研究［D］.西安：西安电子科技大学，2012.

Tian Tongwang.Research on technology of identification of convolutional codes［D］.Xi′an：Xidian University，2012.

［13］王琳，徐位凯.高效信道编码译码技术及其应用［M］.北京：人民邮电出版社，2007：35-61.

Wang Lin，Xu Weikai.High effective channel coding＆decoding technology and its application［M］.Beijing：Posts ＆Telecom Press，2007：35-61.

［14］万哲先.代数和编码［M］.北京：高等教育出版社，2007：406-437.

Wan Zhexian.Algebra and coding［M］.Beijing：Higher Education Press，2007：406-437.