针对有向图的局部扩展的重叠社区发现算法＊

张海燕 梁 循 周小平

（1.中国人民大学信息学院，北京，100872；2.宁夏大学数学计算机学院，银川，750021）

引 言

随着Web 2.0的深入应用，虚拟社会网络已经成为人们生活的重要组成部分，在不同的社会网络中，人们发现个体之间往往存在某些共同特性，即网络的群体特性［1，2］。一般情况下，把内部联系紧密、外部联系稀疏的一群个体称为社区，它反映了网络元素之间的拓扑关系和功能实体，在不同的应用领域，社区代表不同的实体关系群。从巨大的社会网络中挖掘出社区的过程被称为社区发现，是社会网络分析的一个基本任务［1］。因此，发现并分析网络所隐藏的社区结构对了解现实生活中各种社会网络具有重要的意义，在生物学、计算机科学以及社会学等领域都有着广泛的应用［3］。

尽管社区发现已经受到研究者们广泛关注，但是，迄今为止大部分的研究成果都集中于无向图的社区发现［4］。依据无向图的社区发现算法的核心思想，本文将其划分为非重叠和重叠社区发现两类算法，算法划分的结果如图1所示。其中，图1上半部分表示非重叠社区发现算法，非重叠社区发现可看作是硬分类，即每个结点有且仅能属于一个社区；图1下半部分表示重叠社区发现算法，重叠社区发现是软分类，是指网络中的结点可属于多个社区。最早的非重叠社区发现算法应追溯到基于图论的图分割算法［5］，其是解决社区发现问题的最直接方法，也是一种优化方法，但其不足是需要事先指定社区数目。2004年Girvan和Newman提出了经典的GN（Girvan-Newman）算法［6］，边介数概念是GN算法的核心内容，通过删除边介数高的边从而分裂得到整个网络的社区结构，但是，GN算法由于计算量大而很难适用于结点数目上万级的大型复杂网络［3］。同年Newman在PNAS会议上又提出了衡量社区划分优劣的模块度Q概念［7］，之后，最大化模块度的自下而上的合并算法和优化模块度的发现算法被研究者广泛提出。尽管最大化模块度Q一度成为衡量社区划分优劣的依据，但是由于其依赖于全局的网络拓扑结构，会导致大的计算量［5］，而且，分辨率限制的问题也是模块度优化方法的症结。随着社会网络的不断发展以及研究工作的深入，研究者发现社区的重叠性是个显而易见的网络特性，忽略重叠性会降低所发现社区的质量，也会掩盖重叠结点所隐藏的重要信息而造成结点的误判，但是，重叠性也是社区发现中难以量化的属性，给社区发现算法带来了新的难点［5，8］。2005年Palla等提出派系过滤（Clique percolation method，CPM）算法［9］，CPM算法的本质是认为典型的社区应是全连通的完全子图，全连通子图之间共享的结点是重叠结点，其主要目的就是找到紧密相连的完全子图，尽管CPM算法对重叠社区的发现一般来说很有效，但搜索完全子图非常耗时，而且完全子图的大小值k不易确定。2007年Gregory［10］在第11届欧洲国际数据挖掘原理与发现会议上提出改进GN算法的重叠社区发现算法（Clusteroverlap Newman Girvan algorithm，CONGA），但由于CONGA算法通过分裂结点为多个克隆结点来解决重叠结点的问题，因此，其仍然无法克服GN算法计算量大的问题。2009年Lancichinetti［11］提出局部测量拟合度的社区发现算法（Local fitness measure，LFM）从局部拟合构造社区，局部性反映了社区的自然特性［12］，但随机选择初始节点会影响LFM算法的社区发现结果。尽管重叠社区发现算法受到了研究者的关注，但是重叠性的衡量标准仍然没有得到有效解决，如何衡量结点与社区的重叠程度，还需进一步研究。

在现实世界的复杂网络中，链接关系并不总是对称的或无方向的，针对这类具有非对称的有方向关系所构造的图，无向图中的社区发现算法不能直接适用，如果忽略了网络中关系的方向性，会丢失一些隐藏的重要信息［13］。基于有向图的社区发现是社会网络研究中相对较新的发展点，目前也有了一些探索性的研究成果。2011年Satuluri［14］提出了对称化有向图的方法，基于结点之间的指向边与被指向边的相似性对称化有向图的链接矩阵，由此达到有向图变无向图的目的。然而，由于涉及到矩阵的各种运算，对于数据量很大的网络结构，该方法的计算性能受到限制。也有研究者演变无向图社区发现中的模块度、谱的概念到有向图中，给出有向图下相应的定义和社区发现的目标函数，从优化目标函数的角度出发进行社区发现。还有从实际应用领域出发研究符合有向边实际意义的有向图社区发现算法。由于有方向关系的网络结构中，方向往往表达一些重要的信息且无法像无向图那样对称处理，方向意味着信息流动的走向以及信息传播的趋势，因此，有向图的社区发现主要还应从方向入手来解决问题。本文首先提出了基于k-Path的共社区邻近相似性的概念和计算方法及局部扩展的重叠社区发现算法（Local and wave-like extension algorithm of detecting overlapping community，LWS-OCD）算法。

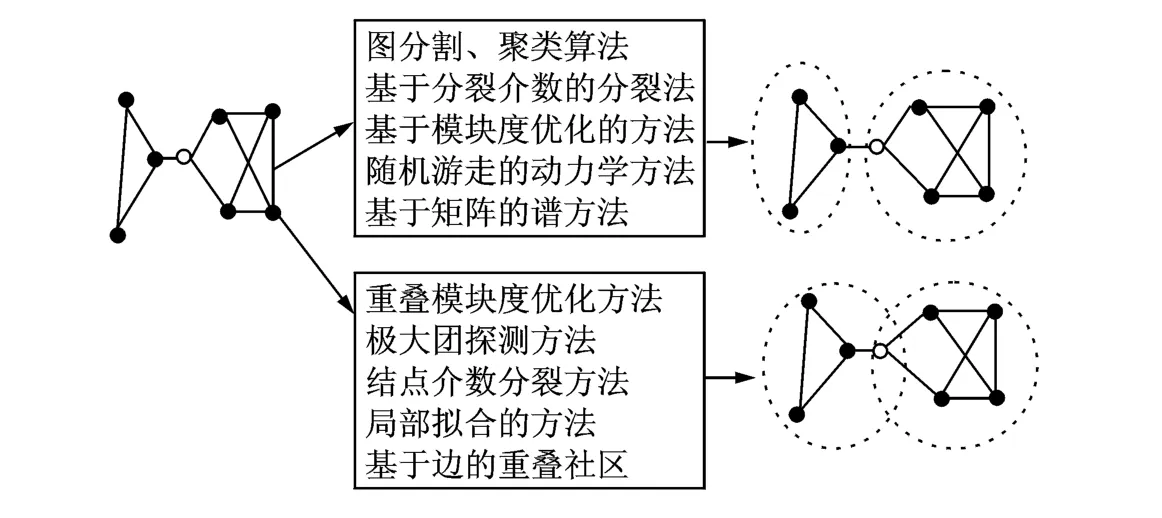
图1 无向图的社区发现算法分类Fig.1 Classification of community detection in undirected network

1 共社区邻近相似性计算

为了衡量网络中结点之间在关系网络中的聚集程度，本文首先提出了共社区邻近相似性的概念，共社区邻近相似性描述了任意两个结点在同一个社区的邻近程度，同时给出了计算共社区邻近相似性的计算方法，这个计算方法适用于无向图也适用于有向图。其次，为了解决有向图的方向问题，本文提出转换有向图为带权值的无向图的方法，目的是将有向图中的方向信息无损保留到无向图中。

1.1 k-Path的共社区邻近相似性

尽管在无向图中，结点之间的链接关系无方向，然而，从实际网络应用中会发现，链接关系中隐藏着信息的走向，因此，结点之间的链接关系更多地是表现为信息在结点之间传播。那么，若两个结点之间有多条链接的通路，表明这两个结点之间信息传播的渠道更多，意味着两个结点联系得更紧密，或者说两个结点信息交流得更便捷，因此，多通路特性反映出两个结点在同一个社区的机率会增大。在有向图上进行社区发现，不能直接延用无向图中的方法，因为有向图中的边是非对称的，方向性蕴含着有价值的信息。正像文献［13］中所描述的那样，很多在无向图中常用的概念移植到有向图中就不适用了，比如说：社区内的边密度和社区外的边密度，当把密度的概念直接用到有向图时，有向边的方向就会被忽略。对于有向图来说，方向是个很关键的因素，并且方向代表着信息流动的可能性，与无向图中信息传播的原理一样，结点之间的链接通路越多，结点之间信息流动得更频繁，那么结点之间的联系会更紧密，因此，多通路特性在有向图中不仅衡量了方向性的强弱关系，同时也反映了结点在同一社区的可能性大小。总之，无论对于无向图还是有向图，多通路特性都可表明图中结点之间在同一社区的邻近相似性。为了说明方便，本文在有向图上描述相应的概念，但是，概念对于无向图同样适用。

定义1k-Path通路

假定G＝〈V，E〉表示有向图，V是结点集，E是有向边集，k是大于0的正数，k-Path通路指的是由边序列e1，e2，…，ek所形成的通路，即经过k条边的单向通路。若G是无向图，则表示结点之间经过k条边的通路。

定义2 共社区邻近相似性

假定G＝〈V，E〉表示有向图，V是结点集，E是有向边集，L是大于0的正数，共社区邻近相似性SL（a，b）指的是：∀a，b∈V，结点a与结点b分别经过1-Path，2-Path，…，L-Path通路的总数之和。换句话说，结点a到达结点b经过1条边、2条边、直到L条边的所有通路之和，定义如式（1）所示

1.2 有向转换为无向的方法

在共社区邻近相似性概念的基础上，令G为初始的有向图，G＝〈V，E〉，为转换后的无向图，其中W是边的权值集合，有向图G到无向图的转换策略为：（1）＝V；（2）若SL（a，b）＞0或SL（b，a）＞0，则e＝（a，b）∈；（3）若e＝（a，b）∈，则We＝SL（a，b）＋SL（b，a）。

转换策略在不丢失有向图的方向信息的情况下，将方向转换为无向图中边的权值，即为带权无向图［15］，其中的权值代表结点之间在同一社区的邻近相似性。

2 局部扩展的重叠社区发现算法

在现实生活中，社区的形成一般是从一些小群体开始的，每个人无论在真实生活中还是在虚拟世界中，往往都是先从熟悉的生活圈子或是个体出发，即从整个关系网络中的局部形成规模，然后再不断地扩张和延伸，因此，对于实际的复杂网络，小群体和局部性就是社区的自然特性。本文提出的局部扩展的社区发现算法是先找出关系网络中的联系相对紧密的“小群体”，然后，再通过这些“小群体”之间的关系来判断是否能构成更大的“群体”，最终形成整个关系网络中的社区结构。

文献［11］中提出的LFM算法是从局部拟合构造社区的发现算法，LFM算法通过试探当前社区波及到的所有结点来判定结点是否属于当前的社区，然而，事实上，在圈定社区内的结点时，没有必要去试探所有的结点，因为按照六度分割原理，社区中的任意结点之间最多通过6个人就可达到联系，因此，本文认为只需要判定某个范围内的结点是否属于当前社区即可，而且探测过程中，根据结点之间的相似性大小来优先选择结点，势必会缩短社区形成的时间，本文将有限探测范围所波及的结点确定为小社区，之后再以这些小社区为基础，构成更大社区。

2.1 概念定义

2.1.1 结点与社区的贴近度

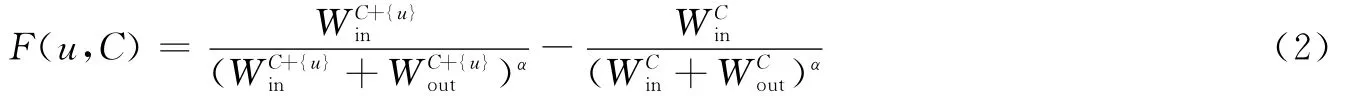
式中：α是分辨率系数，用来控制社区的大小；C是社区，C＋｛u｝是指在社区C中加入结点u形成新社区，是指社区C内的全部边的权值之和，是指有且仅有一个结点在社区C内的边的权值之和。式（2）目的是用来判定结点是否能加入到社区中，意义是当社区C中添加了结点u形成新的社区，若所形成的新社区内部边的权值之和增幅高于原先没有添加结点u时的内部权值之和的增幅，说明添加结点u不仅扩展了社区C，而且也增大了社区C内部的紧密度，由此，可判断结点u就应加入到社区C中，否则，说明结点u与社区C之外的结点链接更紧密。

2.1.2 重叠结点与社区的重叠度

重叠度的概念是衡量重叠结点与其每个所属的社区之间的重叠程度。式（3）中，当结点u是重叠结点时，它属于多个社区，假定社区发现算法划定的社区个数为n个，式（3）中的分母表示结点u所属于的每个社区的贴近度总和，式（3）的分子表示结点u属于当前社区C的贴近度，因此，式（3）表明结点u属于当前社区C的贴近度占其所属的所有社区的贴近度的比重。由此，OD（u，C）值越大，说明结点u与当前社区C的重叠度越高，反之，表明结点u与当前社区C的重叠度低。OD（u，C）是动态变化的，它与社区当前的状态有关，因此，在整个复杂网络的社区没有固定时，重叠结点与社区的重叠度会随着社区大小而改变。

2.1.3 相邻社区

一旦“小群体”（或称之为小社区）形成，整个网络的状态就变成“小群体”与“小群体”之间的交互，如果“小群体”之间有频繁的联系或是紧密性，那么这两个“小群体”就会在未来组合成更大的群体，反之，这些“小群体”就会以独立的群体成为网络中的社区。对于复杂网络，组合为更大社区的最直接办法就是两两小社区互相判断组合，然而，根据现实生活中实际社区的观察，两个社区之间能组合的可能性是社区之间或多或少都会有联系。因此，本文把具备组合条件的两个社区称之为相邻社区，即相邻社区应该满足如下条件之一：（1）两个社区之间有公共的结点，即重叠结点；（2）两个社区之间有多条链接边。只有符合这些条件的两个社区，才有组合为更大社区的基础。相邻社区的定义意味着并不需要所有的小社区互相判定，而只需要在相邻社区之间判定组合，这实际是对小社区在组合之前进行了筛选。

2.1.4 相邻社区之间的贴近度

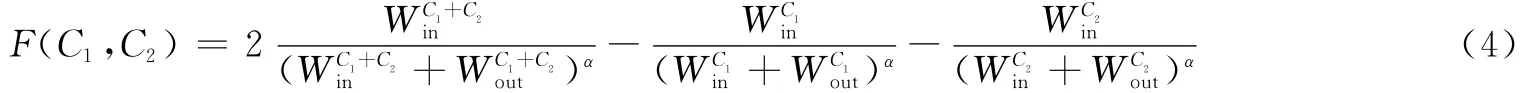
2.2 LWS-OCD算法

局部扩展的重叠社区发现算法分为两部分，（1）局部波动扩展小社区算法（Local and wave-like extension algorithm of detecting small communities，LWS），目的是以L为最大波长从起始点波动扩展局部小社区；（2）归并小社区的重叠社区发现算法（Overlapping community detection algorithm of merging small communities，OCD），合并局部小社区构造网络的全局重叠社区结构。

2.2.1 局部波动扩展小社区

文献［11］中提出的LFM算法也是局部扩展的算法，然而，LFM算法是随机选择初始结点，并且在局部区域选择结点时并不考虑结点之间的不同，结点与结点之间是没有关系强弱之分，随机选择结点的所有邻接结点判断并选择其中拟合度最大的结点，当结点的邻接数目很多时，探测的过程很费时。本文认为结点之间的关系应有强弱之分，强关系的结点应比弱关系的结点更早地被选入社区。

LWS算法首先选择结点度数最高的结点作为社区的起始点，这样的结点链接其他结点的数目多，更有可能是小社区中的中心结点，也是与周围结点联系频繁的结点。其次，根据式（2）从波长1直到最大波长范围L逐圈选择并判断结点是否要加入社区，最大波长范围L可根据具体问题来设定。当然，按照六度分割原理，网络的波长上界为6。在选择结点时，本文按照表达强弱关系的共社区邻近相似性权值对结点进行筛选，优先选择与中心结点在同一社区相似性最高的结点，由此可减少结点的选择时间和误判。最后，局部构造小社区的过程在最大波长范围下停止。LWS算法的具体过程如下所示。

输入：L：最大波长；G（V，E，W）：带相似性w的无向图；阈值θ；

输出：LC＝（C1，C2，…，CI）：小社区集合。

（1）选择结点中度数最大的结点u作为起始点并加入社区CI（初始I＝1），推进的步长T为1；

（2）For（T＜L）Do

以起始点u为波动中心点，结点u的邻接边数为T的结点构成备选结点集合；

（3）For（备选结点集合不空）Do

依次选择备选结点集合中的邻近相似性最高结点v；

计算结点v与社区CI的贴近度F（CI，v）；

IF（贴近度F（CI，v））＞阈值θThen结点v加入社区CI中构成新的社区CI。

While（社区CI有变化）Do

重新计算社区CI中每个结点w与社区的贴近度；

若结点w与社区CI贴近度为负，则将结点w移出社区CI；

End while（社区CI有变化）

End For（备选结点集合不空）

步长T增加1，返回到（2）

End For（T＜L）

（4）若存在未分区的结点，社区数目I＋1，则选择下一个结点度最大的结点作为起始点u，返回（1）。

2.2.2 小社区组合

算法LWS结束后会获得局部稳定的小社区，这些小社区是联系紧密的“小群体”，但还不是最终的社区结构，因为“小群体”是整个网络的初始划分，还需要进一步探究“小群体”之间的关系，以此判断是否达到整个网络结构划分的稳定态，所以，算法OCD的目的是合并小社区形成整个网络的社区结构。

首先，依据相邻社区的定义来判定社区之间是否是相邻社区，然后，在判定为相邻社区的两个社区之间测量社区之间的贴近度，若两社区之间的贴近度大于事先设定的阈值，则合并相邻社区为一个社区，最后，不断迭代此过程，直到社区之间无合并，则迭代结束时的社区结构就是整个网络的社区结构。

OCD算法的具体过程如下所示。

输入：LC＝（C1，C2，…，CI）：小社区（算法LWS的结果）；阈值δ；

输出：C＝（C1，C2，…，CK）：社区。

（1）小社区集合作为社区的初始集合C＝LC，K＝I，即C＝｛C1，C2，……，CK｝；

（2）While（i＜K）Do

从社区向量C中Ci之后找出社区Ci的相邻社区Ct；

计算社区Ci与社区Ct之间的贴近度F（Ci，Ct）；

IFF（Ci，Ct）＞阈值δThen

合并社区Ci，Ct加入社区C中形成新社区Ci；

K＝K-1；

重新计算新社区Ci中每个结点与新社区Ci的贴近度。

End IF

变换下一个小社区i＝i＋1；

End While（i＜K）

（3）循环结束，全局社区C构造完成，所形成的C即为网络结构的社区；

（4）确定社区C中的重叠结点；

（5）计算重叠结点与每个所属社区的重叠度。

2.2.3 LWS-OCD算法的计算复杂性分析

重叠社区发现算法的复杂性是很难精确估计的，因为它和网络的大小、重叠结点的个数以及网络的社区结构等因素相关，同时，在实践中，算法的效率与数据所采用的数据结构以及机器性能等因素也有关。但是，本文从理论上粗略地分析LWS-OCD社区发现算法的计算复杂性。

LWS算法的时间主要消耗在挑选结点的过程，最耗时的过程有两个：（1）在当前波长T所涉及的范围圈内结点的贴近度计算，假设此时圈定范围的结点数目为NT，那么计算时间就是O（NT）。（2）一旦有新结点加入社区，就需重新调整当前社区内已有结点与社区贴近度的变化，若有某些结点的贴近度减少以致低于阈值或为负值，则需要将这些结点移出当前社区，这个过程会不断重复，直到社区内的结点的贴近度都超出阈值。那么，假设此时社区内的结点个数为NC，这个过程的最坏情况是所有结点都被依次移出，时间复杂度为O（N2C），然而，本文提出的LWS-OCD算法为了避免这种情况，每次选择共社区邻近相似性最高的结点判断，大大减少了与社区弱相关结点的误移入而造成结点移出操作，故此部分的时间复杂度可近似为O（NC）。最终，整个LWS算法的时间复杂度近似为O（L×NT×NC），其中的NT，NC都是小于结点个数N的，L是波长。而对于LFM算法，因为其要遍历所有当前社区的邻接点，这个邻接点数目远远大于离中心点步长为T的NT，所以其计算贴近度的时间是大于O（NT），且LFM算法的初始结点随机选择，结点选择的不合适会增加结点的移出操作，所以其复杂性高于本文的LWS算法。对于OCD算法而言，它是在小社区的基础上的两两合并，小社区的数目是远远低于网络结点数目N，假设小社区的数目为Cn，那么这个过程最坏的情况下的时间复杂度O（），然而，大多数网络结构在LWS算法结束时刻会达到初始稳定态，因此，此部分的时间复杂度近乎为线性O（Cn）。综合算法LWS和算法OCD两部分，LWS-OCD算法的时间复杂度为O（L×NT×NC＋），即好的情况下可近似为O（n2）的量级。

3 实验结果与分析

3.1 测试数据集

本文所采用的两组真实数据集网络如下：第1组数据是有向图的数据集，来源于最大的社会网络研究组织。选择了其中的数据集Wiki-Vote。Wiki-Vote数据集是维基百科（Wikipedia）网站中2008年百科版块中的投票数据，包括7 115个结点和103 689条边。第2组数据是无向图的数据集，选择海豚关系网Dolphins数据集［16］，包括62个结点和159条边；另外一个是科学家合作网Netscience数据集，包括1 589个结点和2742条边。

本文的实验环境是在CPU为Intel i5 3.2GHz，内存为4GB的64位Win7机器上，共社区邻近相似性的计算以及有向图转换为带权无向图分别采用Visual C和Matlab7.0的编译环境。为了充分说明算法的有效性，本文选择文献［11］中提出的局部拟合的LFM重叠社区发现算法进行实验对比，LWSOCD算法和对比算法LFM采用Visual C的编译环境完成实验的测试和验证任务。

3.2 共社区邻近相似性的实验结果和分析

3.2.1 时间效率的对比

无论是无向图还是有向图，共社区邻近相似性是社区发现算法的基础，也是图中结点相似性的一种有效测量方法。本文采用了Matlab的编译环境，运用矩阵运算的优势来完成共社区邻近相似性的计算过程，针对有向图数据集Wiki-Vote和无向图的数据集Netscience，完成在不同的路径长度下计算共社区邻近相似性所需时间的对比实验，实验结果如图2所示。在图2中，Netscience的网络结点数目少，因此所用时间就短，而Wiki-Vote的网络结点数目是Netscience的4倍多，因此其所用时间明显比Netscience多。此外，随着链接路径的长度增大，共社区邻近相似性的计算时间也会呈线性增加。由此可知，共社区邻近相似性的计算时间主要还是取决于网络的结点数目和链接情况，若链接相对密集且结点数目很多，则共社区邻近相似性的计算时间就长，若链接相对稀疏则邻近相似性的计算时间短。事实上，根据小世界网络的特性可知，任何两个结点之间最多通过6个人就可达到彼此的联系，而且，从现实生活中观察也可看到，若两个结点属于共同社区，通常这样的结点联系会更频繁些，意味着这样的结点之间的链接通路都不会太长，否则，它们之间的交互可能性就会很低，表明它们之间在同一社区的可能性也会降低。由以上原因和实验效率的观察，本文认为链接通路长为3是共社区邻近相似性的最佳选择。

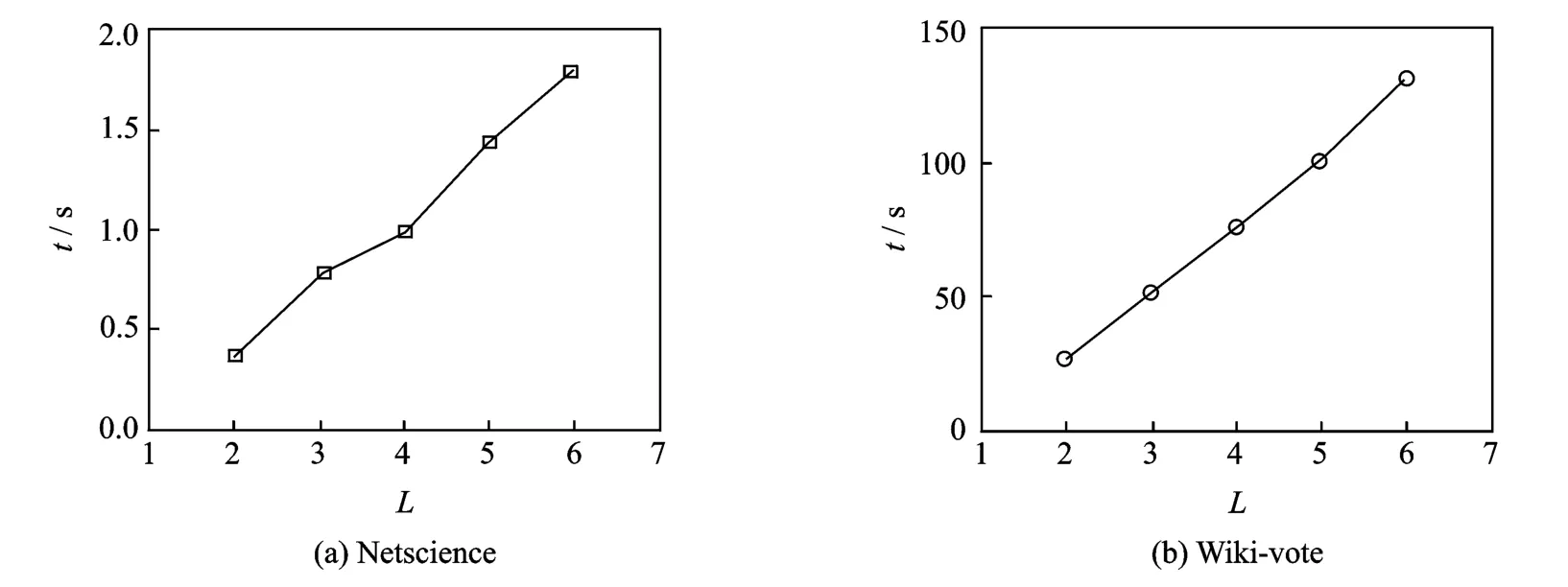
图2 共社区邻近相似性的计算复杂性Fig.2 Computational complexity of co-community similarity

3.2.2 对社区发现算法的影响

共社区邻近相似性对社区发现算法所起的效果也不容忽视，为了说明共社区邻近相似性所起的作用，图3中分别列出了LFM算法在未加和加上共社区邻近相似性的Dolphins数据集网络下的社区发现结果。从图3（a）中可以看到，当在原始Dolphins无向图上实现LFM算法时，网络形成了唯一的社区，而在图3（b）中，首先为原始的无向图构造最大链接通路长为3的共社区邻近相似性的带权值无向图，然后在带相似性权值的图上完成LFM社区发现算法，可以看到，此时的网络被清楚地分为左下部和右上部黑色结点组成的两个密集社区，而其中的灰色结点为网络的重叠结点，这个社区划分结果与GN算法在Dolphins数据集上所进行的社区划分结果相一致。由此可见，共社区邻近相似性加权会起到对网络中同一社区结点聚集的作用，有助于社区发现算法实现密集社区划分的效果。

3.3 LWS-OCD算法的实验结果和分析

3.3.1 LWS-OCD算法的有效性对比

为了对比本文所提出的LWS-OCD算法的有效性，分别在Dolphins和Netscience两个无向图数据集中构造各自对应的链接通路长2，3，…，6的共社区邻近相似性的带权无向图，然后，在所构造的带权无向图上完成LWS-OCD算法和LFM算法。图4中给出了LFM算法和LWS-OCD算法所挖掘出的重叠结点个数占总结点的比例。图5中给出了LFM算法和LWS-OCD算法在Netscience数据集上所划分出的社区的个数。Dolphins in 3-Path和5-Path分别对应Dolphins网络在链接通路最长为3和5所构造的共社区邻近相似性的带权无向图，同理，Netscience in 3-Path和5-Path分别对应的是Netscience的带权无向图。在不同的带权无向图中，分别在社区分辨系数α从0.6，0.65，0.70，……，1.6的每隔0.05的条件下实现LFM和LWS-OCD算法。

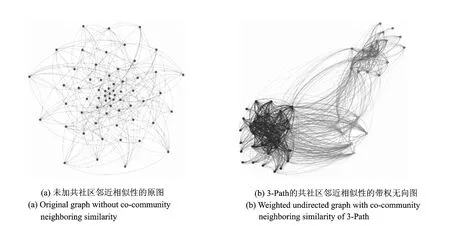
图3 LFM算法的社区发现结果Fig.3 Result of community detection by LFM algorithm

从图4中可看出，本文提出的LWS-OCD算法除了在Dolphins in 5-Path的带权无向图下的后部出现凸起外，在其他的带权无向图下都比LFM算法的重叠结点的比例平稳，即重叠结点的数目不会随社区大小的变化而剧烈变化。事实上，在现实网络中，对于在某一时刻相对静止的网络来说，一旦社区结构稳定后，社区是相对清晰的，那么，重叠结点也会是一定的，不会出现突然的变化。

在图5中，不论是在3-Path的带权无向图还是在5-Path的带权无向图中，LWS-OCD算法与LFM算法所挖掘的社区个数相差不大，由此说明，本文提出的LWS-OCD算法有效。

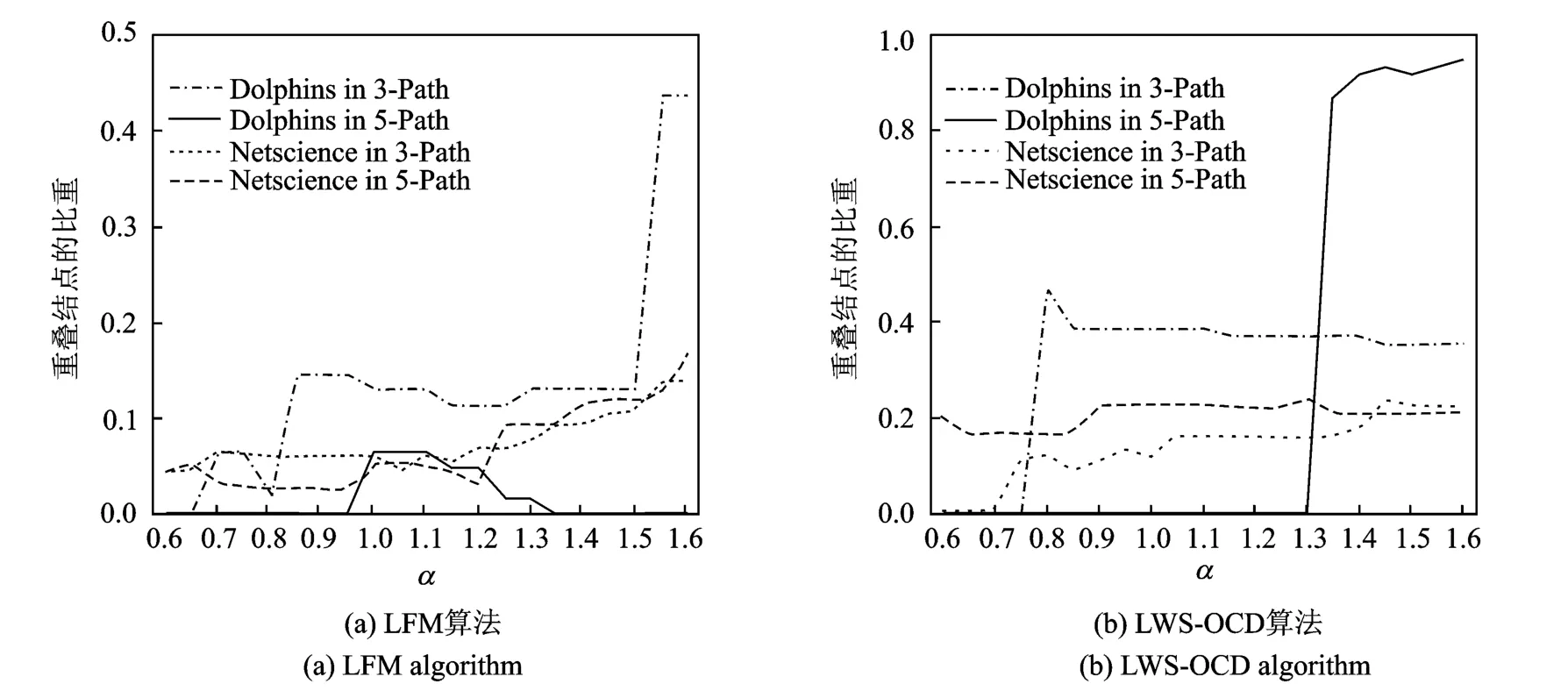
图4 重叠结点在带权无向图上所占的比重Fig.4 Ratio of overlapping node on weighted undirected networks

3.3.2 波长对LWS-OCD算法的影响

为了分析本文提出的LWS-OCD算法受波长范围的影响，在Netscience无向图数据集的链路通路长为3的共社区邻近相似性所构造的带权无向图上，完成波长范围2，3，…，6依次变换且社区分辨率系数α从0.8变化到1.8，步长0.1的本文提出的LWS-OCD算法。图6给出了LWS-OCD算法在不同波长范围下所产生的总社区个数和所挖掘出的重叠结点个数占总结点的比例。

图5 LFM算法与LWS-OCD算法划分Netscience无向图的社区个数Fig.5 Number of community detected by LFM and LWS-OCD algorithms on Netscience network

从图6清楚地看到算法当波长范围达到3之后，社区数目和重叠结点的个数并不以波长的增大而任意扩张，即波长从4到6时社区数目的个数持平，重叠结点的个数也是重合的，社区结构一方面表现出小世界特性，即局部特性，另一方面也反映出社区结构实际在某一时刻是处于一种稳定态。

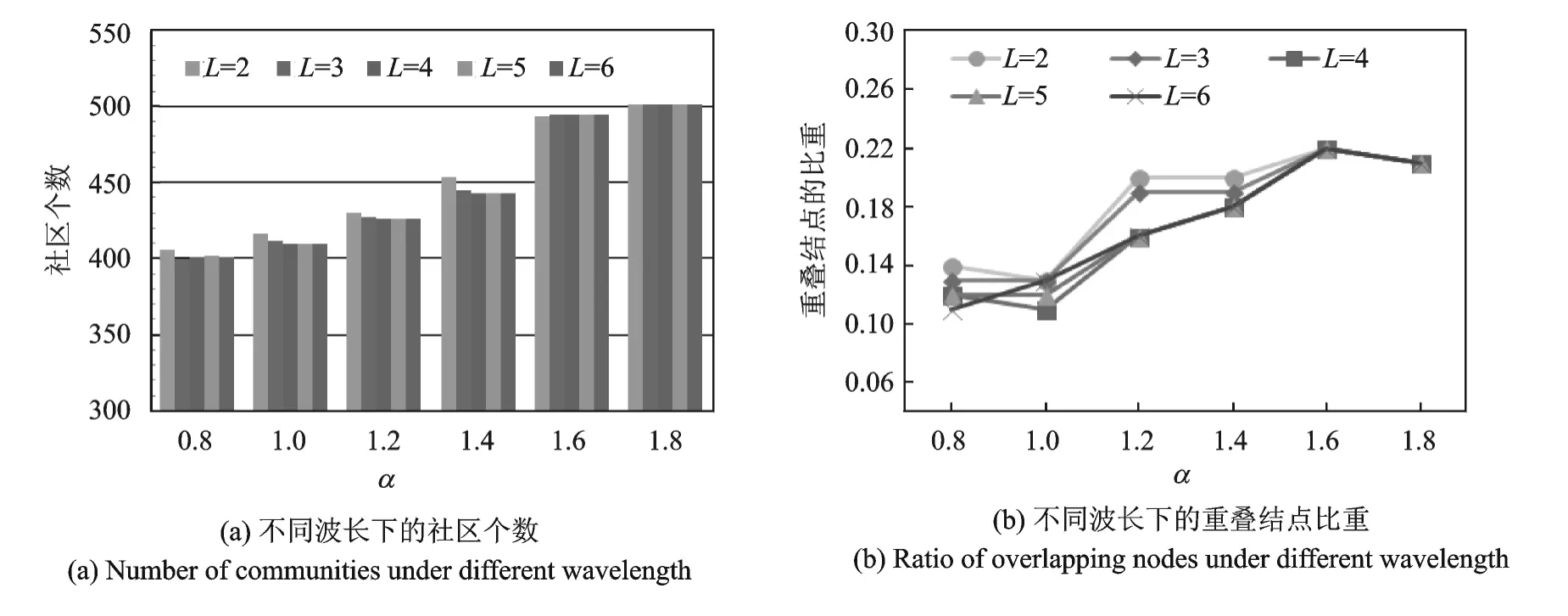
图6 波长范围对LWS-OCD算法的影响Fig.6 Result of wave influencing LWS-OCD algorithm range

4 结束语

本文从信息在网络中的传播规律和流动的方向性出发，提出了共社区邻近相似性的概念，共社区邻近相似性是测量结点在同一社区的可能性，此概念在无向图和有向图中都适用于测量结点之间的相似性。并基于此概念，给出了有向图转换成带权无向图的方法，为有向图的社区发现算法提供了不丢失方向性的有效策略。本文针对带权无向图提出了LWS-OCD局部扩展的重叠社区发现算法，算法的优势在于从社区的“小群体”的自然状态出发，然后由“小群体”不断扩展合并形成更大的社区。LWS-OCD算法不仅避免了分辨率问题，而且与现实生活中社区的发展规律相一致，同时还能为层次型的社区发现做些铺垫工作。本文下一步的工作是扩展算法到并行环境，以此来提高LWS-OCD算法在大数据复杂网络中的可扩展性。另外，针对有向图的社区发现算法是当前社区发现算法的研究热点，本文将提出直接在有向图上进行社区发现的算法，即不经过有向到无向的转换，由于有向图中方向性的存在，这必然是个有挑战性的工作。

［1］ Easley D，Kleinberg J.Networks，crowds，and markets：Reasoning about a highly connected world［M］.Cambridge：Cambridge University Press，2010.

［2］ 周耀明，李弼程.一种自适应网络舆情演化建模方法 ［J］.数据采集与处理，2013，28（1）：69-76.

Zhou Yaoming，Li Bicheng.Adaptive evolution modeling method of internet public opinions［J］.Journal of Data Acquisition and Processing，2013，28（1）：69-76.

［3］ Tang Lei，Liu huan.社会计算：社区发现和社会化媒体挖掘 ［M］.文益民，闭应洲，译.北京：机械工业出版社，2012.Tang Lei，Liu Huan.Community detection and mining in social media［M］.Beijing：China Machine Press，2012.

［4］ Fortunato S.Community detection in graphs［J］.Physics Reports，2010，486（3）：75-174.

［5］ 程学旗，沈华伟.复杂网络的社区结构 ［J］.复杂系统与复杂性科学，2011，8（1）：57-70.

Cheng Xueqi，Shen Huawei.Community structure of complex networks［J］.Complex Systems and Complexity Science，2011，8（1）：57-70.

［6］ Newman M E J，Girvan M.Finding and evaluating community structure in networks［J］.Physical review E，2004，69（2），026113.

［7］ Newman M E J.Detecting community structure in networks［J］.The European Physical Journal B-Condensed Matter and Complex Systems，2004，38（2）：321-330.

［8］ Xie J，Kelley S，Szymanski B.Overlapping community detection in Networks：the state-of-the-art and comparative study［J］.ACM Computing Surveys，2013，45（4）.43：1-35.

［9］ Palla G，Derényi I，Farkas I，et al.Uncovering the overlapping community structure of complex networks in nature and society［J］.Nature，2005，435（7043）：814-818.

［10］Gregory S.An algorithm to find overlapping community structure in networks［C］／／Proceedings of Knowledge Discovery in Databases：PKDD 2007，11th European Conference on Principles and Practice of Knowledge Discovery in Databases.Warsaw，Poland：Lecture Notes in Computer Science，2007：91-102.

［11］Lancichinetti A，Fortunato S，Kertész J.Detecting the overlapping and hierarchical community structure in complex networks［J］.New Journal of Physics，2009，11（3），033015：1-18.

［12］Chen D，Shang M，LV Z，et al.Detecting overlapping communities of weighted networks via a local algorithm［J］.Physica A，2010，389（19）：4177-4187

［13］Malliaros F D，Vazirgiannis M.Clustering and community detection in directed networks：A survey［J］.Physics Reports，2013，533（4）：95-142.

［14］Satuluri V，Parthasarathy S.Symmetrizations for clustering directed graphs［C］／／Proceedings of the 14th International Conference on Extending Database Technology.［S.l.］：ACM，2011：343-354.

［15］De M P，Ferrara E，Fiumara G，et al.Enhancing community detection using a network weighting strategy［J］.Information Sciences，2013，222：648-668.

［16］Lusseau D，Schneider K，Boisseau O J，et al.The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations［J］.Behavioral Ecology and Sociobiology，2003，54（4）：396-405.