一类离散MIMO系统的神经网络自适应输出反馈容错控制
2015-07-25王占山
刘 磊, 王占山
一类离散MIMO系统的神经网络自适应输出反馈容错控制
刘磊,王占山
(东北大学信息科学与工程学院,沈阳110819)
针对一类离散多输入多输出(MIMO)严格反馈系统,提出了基于神经网络的输出反馈容错控制.由于讨论的执行器故障类型有失效和卡死两种情况,提出了比例驱动方法,可将这两种故障类型恰当地表示出并便于控制器的设计;同时,由于此类多输入多输出系统不满足匹配条件,通过引入预测控制设计方法,可以克服这一缺陷.考虑到系统中的函数是未知的,利用神经网络具有逼近任意连续函数到任意精度的原理来估计该未知函数,由此证明了本文所提出的方法可以使得系统的所有参数及实际容错控制律均一致最终有界.通过MATLAB实验仿真,有效地验证了此方法的合理性.
容错控制;执行器故障;多输入多输出离散系统;神经网络;输出反馈控制
动态系统的容错控制(Fault Tolerant Control,FTC)是伴随着基于解析冗余的故障诊断技术的发展而发展起来的.针对非线性连续系统的容错控制已有许多成果[1-4],诸如单输入单输出(SISO)系统[5]、多输入单输出(MISO)系统[6]、多输入多输出(MIMO)系统[7]等.随着互联网及计算机演算的发展,离散系统比连续系统更能描述实际的控制系统[8],因为电脑的运算往往会用到采样技术.目前,针对非线性离散系统的容错控制也已成为热点,并取得了一些研究成果[9-12].但是,这些在离散系统中的容错控制方法,都是在状态反馈的基础上建立的.
基于输出反馈的离散系统的控制理论已得到人们的广泛研究[13-16].文献[13]中,针对带有服务质量约束的网络控制系统,提出了基于输出反馈的镇定化控制器.文献[14]中,基于网络化的运动系统,一种改进的鲁棒静态输出反馈PID控制策略被提出.然而,这两种输出反馈的控制方法,均需要满足匹配条件,即系统的未知动态必须与控制信号在一个通道里面.文献[16]中,针对不满足匹配条件的离散系统,灵活运用预测控制方法,提出了一种基于未知方向的输出反馈神经网络控制方法.另外,当系统的执行器发生故障时,系统的正常运行将受到影响,这些方法均不能直接有效地控制系统.
综上所述,本文针对一类离散MIMO系统,考虑执行器卡死或者失效的情况,提出了一种基于神经网络的自适应输出反馈容错控制器.由于故障类型有两种,采用比例驱动法,将这两种故障类型表示成一种凸组合的形式,便于容错控制器的设计.同时,由于控制信道之外,仍然含有未知函数,利用神经网络具有万能逼近的原理来估计该未知函数.通过仿真实验,证明了所提容错控制方法的有效性.
1 系统描述及预备知识
考虑如下含有执行器故障的多输入多输出严格反馈离散系统
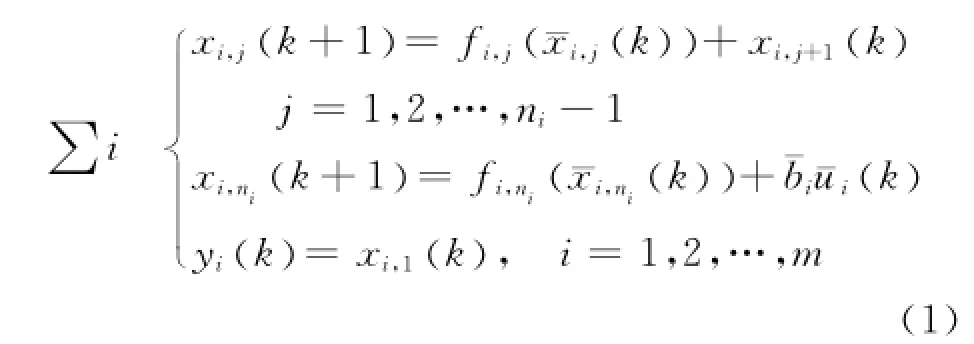
本文所考虑的执行器故障包括卡死和失效两种类型,具体表示为:
卡死
其中:u^ip表示第i个子系统中第p个执行器卡死;kip是卡死时间.即若一个执行器卡死,其相应的输入值就不变了.
失效
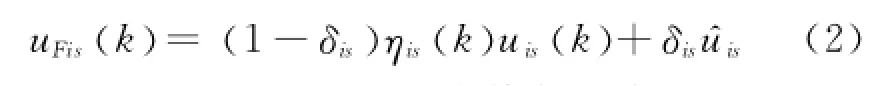
式中,若第i个子系统中第s个执行器卡死,则δis= 1,否则δis=0.
为了方便容错控制器的设计,有如下假设.
假设1第i个子系统里的执行器最多有li-1个是卡死故障,即至少有一个执行器是失效故障.在此情况下,假设系统仍能运行.
假设2期望输出yd()k∈Ωy,k>0是已知光滑的,Ωy是有界紧集.
控制目标设计一个基于神经网络的输出反馈容错控制律,使得每个子系统的输出yi(k)尽可能地跟踪上指定的期望轨迹,并且系统的所有信号均一致最终有界.
2 容错控制器设计
根据文献[15]中的方法,可将系统进行坐标变换,变换结果如下:


于是,可得误差动态方程为

控制器设计步骤如下:
第1步由式中第一个式子,运用文献[5]中提出的比例驱动法,可得和分别的下界和上界.因此有


选择理想控制器
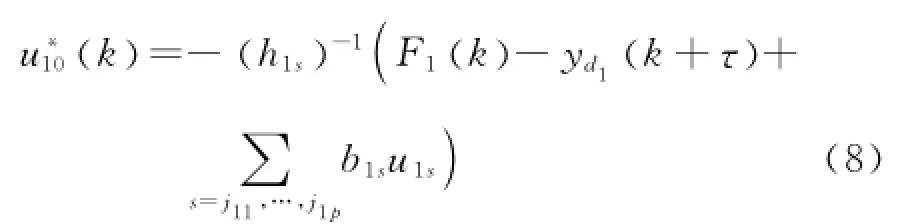

式中:θ1是神经网络最优权重;是径向基函是最优逼近误差;S1(k)=.于是可选择如下控制输入和自适应律:
运用类似如上设计方法设计控制器:
第i步由式中第i个式子,选择理想控制器

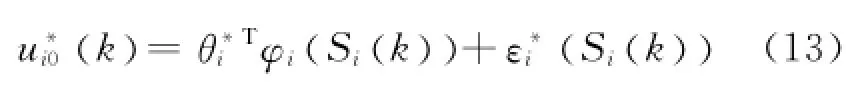

定理1考虑一类带有执行器故障(如式(2)的MIMO离散系统(如式(1)),基于假设1和2,设计自适应律如式(11)和(15)所示,提出自适应容错控制器如式(10)和(14)所示,则该MIMO离散系统的所有信号均一致最终有界.
证明
第1步由式(5)和(7),可知可得
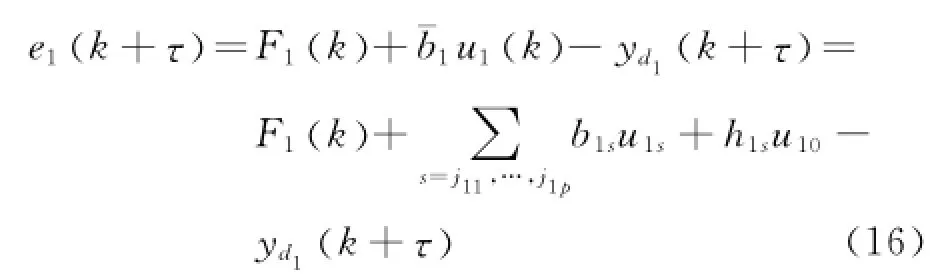

式中,~θT1=θ^T1-θT1是神经网络权重估计误差.
选取如下李雅普诺夫函数
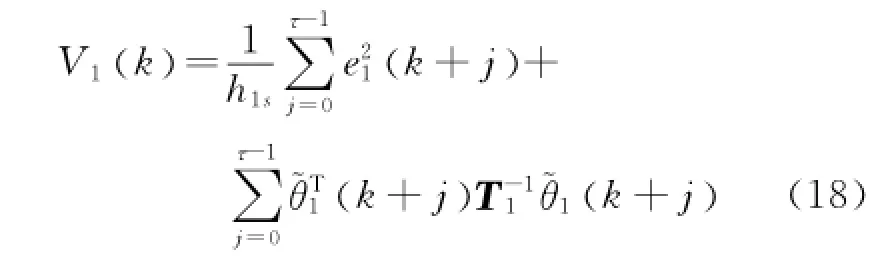
由式(11)和(16),可得
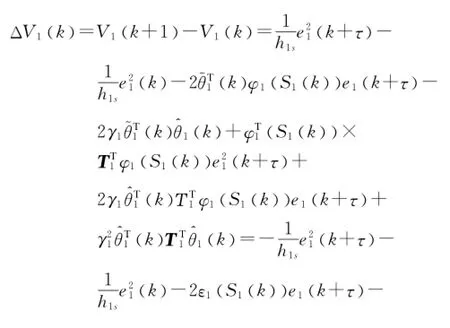
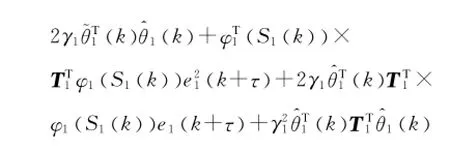
考虑如下不等式:

其中,μ1是神经网络节点数,λmax(Τ1)是Τ1的最大特征值.
因此,有
若设计参数λmax(Τ1)和γ1满足如下条件:
则式(19)可写为

第i(i=2,3,…,n)步选取如下李雅普诺夫函数
应当说,毛主席的心情可以理解,他的希望也不是没有道理。但《红灯记》是按事物内在发展逻辑、系统而完整的文艺创作,如果改变其中的重要人物命运,会使作品伤了元气,失去悲剧的应有力量。所以,闫肃没有改,坚持了自己的尺度,之后多年的演出效果,也证明他是对的。
进行与第1步相同的过程,可得
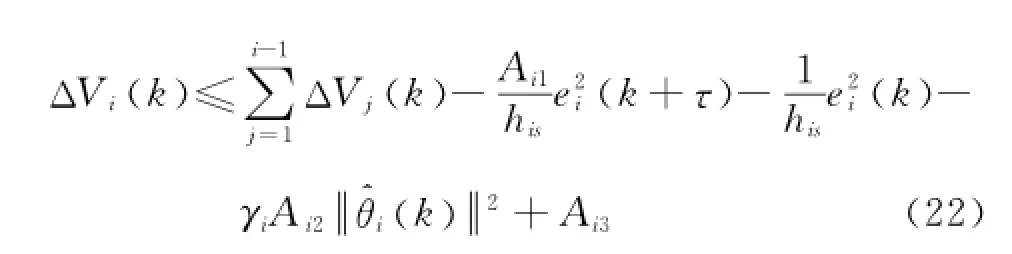
式中:

若设计参数λmax(Τi)和γi满足如下条件:
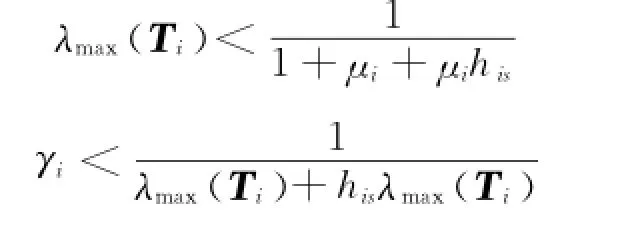
则式(22)可写为

综上所述,对于闭环非线性多输入多输出系统式(1),若选择满足如下条件的设计参数:

3 仿 真
考虑如下MIMO离散系统[14]:

其中:

期望输出信号为:
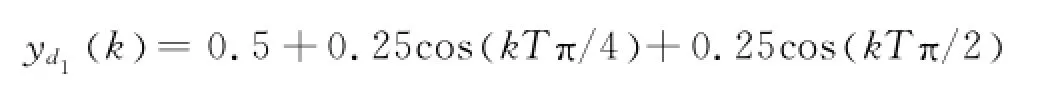

仿真结果如图1所示.图1(a)为第1个子系统的跟踪效果.由图可见,即使执行器失效,其跟踪效果仍然良好.图1(b)为第2个子系统的跟踪效果.当系统发生卡死故障时,系统的跟踪效果有短暂的影响,但随后,跟踪误差也在“零”的小邻域内.

图1 不同故障状况下系统跟踪性能及跟踪误差Fig.1 The tracking performances and tracking errors under different fault
4 结 语
本文建立的基于神经网络的容错控制器通过输出反馈方式给出.被考虑的离散系统不再是SISO
系统,而是扩充到MIMO系统.不仅考虑了执行器的卡死故障,也考虑了执行器的失效故障.通过比例驱动法,便于容错控制的设计.由于MIMO离散系统包含未知函数,利用径向基神经网络可以有效地估计该未知函数.因系统不满足匹配条件,引进预测控制方法,可有效地解决这一问题.最后,通过李雅普诺夫稳定性分析法,证明了闭环系统中的所有信号均一致最终有界.
[1]姜斌,冒泽慧,杨浩,等.控制系统的故障诊断与故障调节[M].北京:国防工业出版社,2009.
[2]王占山,张化光.一类自适应观测器的故障估计性能[J].东北大学学报:自然科学版,2004,25(12):1134-1137.
[3]Wang Z,Li T,Zhang H.Fault tolerant synchronization for a class of complex interconnected neural networks with delay[J].International Journal of Adaptive Control and Signal Processing,2014,28 (10):859-881.
[4]Wang Z,Zhang H.Design of a bilinear fault detection observer for singular bilinear systems[J]. Journal of Control Theory and Applications,2007,5 (1):28-36.
[5]Wang W,Wen C.Adaptive actuators fault compensation for uncertain nonlinear systems with guaranteed transient performance[J].Automatica,2010,46(12):2082-2091.
[6]Tang X,Tao G,Joshi S.Adaptive actuator faultcompensation for nonlinear MIMO systems with an aircraft control application[J].Automatica,2007,43 (11):1869-1883.
[7]Liu L,Wang Z,Zhang H.Adaptive NN faulttolerant control for discrete-time systems in triangular forms with actuator fault[J].Neurocomputing,2015,152:209-221.
[8]Mahmoud M.Stochastic stability and stabilization for discrete time fault tolerant control system with state delays[C]//American Control Conference.Seattle,USA:American Automatic Control Council,2008:1040-1045.
[9]Jiang B,Zhang K,Shi P.Integrated fault estimation and accommodation design for discrete-time Takagi-Sugeno fuzzy systems with actuator faults[J].IEEE Trans Fuzzy Syst,2011,19(2):291-304.
[10]Thumati B,Feinstein M,Sarangapani J.A modelbased fault detection and prognostics scheme for Takagi-Sugeno fuzzy systems[J].IEEE Transactions on Fuzzy Systems,2014,22(4):736-748.
[11]Zhang D,Yu L.Fault-tolerant control for discretetime switched linear systems with time-varying delay and actuator saturation[J].Journal of Optimization Theory and Applications,2012,153(1):157-176.
[12]Peng C,Tian Y C,Yue D.Output feedback control of discrete-time systems in networked environments [J].IEEE Transactions on Systems,Man and Cybernetics,Part A:Systems and Humans,2011,41(1):185-190.
[13]Zhang H,Shi Y,Mehr A S.Robust static output feedback control and remote PID design for networked motor systems[J].IEEE Transactions on Industrial Electronics,2011,58(12):5396-5405.
[14]Zhang J,Ge SS,Lee T H.Output feedback control of a class of discrete MIMO nonlinear systems with triangular form inputs[J].IEEE Transactions on Neural Networks,2005,16(6):1491-1503.
[15]Yang C,Ge S S,Xiang C,et al.Output feedback NN control for two classes of discrete-time systems with unknown control directions in a unified approach [J].IEEE Transactions on Neural Networks,2008,19(11):1873-1886.
[16]Wang Z,Zhang H,Li S.Robust fault diagnosis for a class of nonlinear systems with time delay[J]. Journal of Harbin Institute of Technology:New Series,2007,14(6):884-888.
(编辑俞红卫)
NN-Based Adaptive Output Feedback Fault Tolerant Control for MlMO DiscreteTime Systems
LIU Lei,WANG Zhanshan
(School of Information Science and Engineering,Northeastern University,Shenyang 110819,China)
In view of a class of MIMO discrete-time systems,a neural network(NN)-based output feedback fault tolerant control(FTC)was presented.On account of the considered actuator faults containing both of loss of effectiveness and lock-in-place,the proportional-actuation method was utilized to combine the two fault types into a proper expression to design the FTC conveniently.Meanwhile,due to the failure of the MIMO systems in satisfaction with the matching condition,this restriction could be solved by bringing in predictive control technique.Based on the NNs’approximate ability of estimating any function to arbitrary precision,the unknown system function was approximated by using NNs.Then,it’s proved that all the signals and the fault-tolerant controller in the closed-loop systems were uniform ultimate boundedness(UUB).A MATLAB simulation showed the effectiveness of the proposed FTC approach.
fault tolerant control(FTC);actuator fault;MIMO discrete-time systems;neural networks (NN);output feedback control
TP 306.3
A
1671-7333(2015)03-0293-06
10.3969/j.issn.1671-7333.2015.03.016
2015-01-15
国家自然科学基金资助项目(61473070,61433004);中央高校基本科研业务费资助项目(N130504002,N140406001,N130104001);流程工业综合自动化国家重点实验室资助项目(2013ZCX01)
刘磊(1987-),男,博士生,主要研究方向为基于神经网络的大规模系统的故障检测、容错控制.E-mail:liuleill@live.cn
王占山(1971-),男,教授,博士生导师,主要研究方向为非线性控制系统的故障诊断、容错控制方法及其在工业过程中的应用,神经网络系统理论及其应用.E-mail:zhanshan_wang@163.com
