基于拉普拉斯正则化概率主元分析的故障检测

周　乐，　宋执环

基于拉普拉斯正则化概率主元分析的故障检测

周乐，宋执环

（浙江大学工业控制技术国家重点实验室，杭州310027）

概率主元分析（PPCA）及其扩展方法用于过程监测时，只提取了过程数据的全局特征，并未考虑数据的局部结构.当数据的流形结构复杂时，传统的全局建模方法难以获得准确的预测效果.提出了一种基于拉普拉斯正则化的概率主成分（LapPPCA）模型，将数据的流形结构引入到传统概率模型的似然函数中，使得LapPPCA能够同时提出数据的全局和局部特性.同时提出了基于LapPPCA的过程监测模型，并在田纳西-伊斯曼（TE）过程上验证了该方法的有效性.

拉普拉斯正则；概率主元分析过程监测；故障检测

现代流程工业对产品质量、节能降耗和产生成本的要求不断提高.因此，以保障生产安全、提高产品质量为目的的过程监测技术就显得尤为重要，已经成为了实现流程工业综合自动化的关键因素之一［1］.其中，基于多元统计分析的过程监测（MSPM）技术在近年来被广泛研究和应用于实际生产过程.主成分分析（PCA）和偏最小二乘估计（PLS）以及其扩展方法是多元统计分析技术的代表性模型，将原始数据分成低维度的隐变量空间和残差空间，以此来消除数据之间的互相关性并在两个子空间下分别建立统计模型，并评估生产过程是否正常［2-3］.

传统的PCA模型由标准化的线性投影所得到，并确保数据被首先投影到方差最大的方向，而这一定义缺乏了对观测数据和隐变量的概率解释.Tipping等［4］针对这一问题提出了概率主元分析（PPCA）方法.作为概率模型，其参数通过期望最大化（EM）算法估计得到，而EM算法易于处理含缺失值数据的样本并且在处理高维数据时计算效率更高.此外，概率模型通过极大似然估计方法得到，这使得模型对于数据的离群点更加鲁棒［5］.因此，基于PPCA及其扩展模型的过程监测技术已被广泛研究并用于过程监测中［6-8］.

PCA和PPCA模型都只考虑了观测数据的全局结构.近年来，越来越多的学者认为数据是均匀采样于一个高维欧几里得空间的低维流形中.因此，为了从高维数据中恢复数据的低维流行结构，很多流形学习算法被提出，如局部线性映射（Locally Linear Embedding，LLE）、拉普拉斯特征映射（Laplacian Eigenmap，LE）和等距映射（Isomap）等.最近，流行学习算法开始被引入过程监测领域，用于对数据的非线性特征及局部特征的提取，并取得一定的效果［9-10］.

然而，传统的概率模型及其扩展方法均是全局的建模方法，并未考虑数据的流行结构.因此，在进行降维时并不能提取数据的全部信息，尤其当数据的流形结构复杂时更难以获取满意的建模效果.本文提出了一种基于拉普拉斯正则化的概率主成分（LapPPCA）模型，将数据的流形结构通过隐变量的概率分布来表示，即如果两个点在流形上相近，则其隐变量的概率分布也相似［11］.在LapPPCA中，通过近邻点来估计数据的流形结构，并通过图形拉普拉斯算子将流行结构引入到似然函数和EM算法中.因此，Lap PPCA的隐变量同时提取了数据的全局信息和流形结构，以此强化了其特征提取能力，使得基于LapPPCA的特征提取技术能够更准确地表达数据的全部特征.基于Lap PPCA的过程监测模型也会取得更好的监测效果.

1　概率主元分析

在正常工况下采集到二维数据集X=［x1x2…xI］T∈RI×M，其中I为样本数，M为变量数. PPCA模型被定义为［4］

2　拉普拉斯正则化的概率主元分析

式中，x∈RM是归一化后的观测样本，P∈RM×R是负载矩阵，R是隐变量t的维度.观测点x由隐变量的线性组合推衍得到.而隐变量t∈RR被假设服从标准高斯分布.不同于PCA，噪声e∈RM不再作为模型分解的残差，而是也被假设为服从高斯分布：e～N（0，σ2I），其中I是单位矩阵.

由于PPCA是一种全局的建模方法，并未考虑数据的局部特性，即流形结构.因此，在数据的局部特征非常显著时，仅使用基于全局的建模方法很难完整地提取出数据的全部特征，在这种情况下，就需同时提取数据的全局和局部特征，以获取更准确的数据模型.

2.1LapPPCA模型结构

LapPPCA的模型结构与PPCA相似，不同的是，LapPPCA的隐变量t∈RR同时提取了观测变量的方差变化（全局特征）和流形特征（局部特征）.然而，实际过程中，数据的流形特征很难得知.因此，本文采用了近邻点图形法来估计样本点的局部结构.对任意样本点xi，把距离xi欧氏距离最近的前K个点定义为xi的近邻点，每个近邻点的权值定义为

式中：1≤i≤I，1≤j≤I；ω为核参数.

利用样本的K个近邻点，每个采样的流形结构可以被估计为［11］

式中：Γ=（E（t1｜x1），E（t2｜x2），…，E（tn｜xn））T；Dii=∑jSij；L=D-S被称为图形拉普拉斯算子.

从Ri的定义得知，两个样本点隐变量的分布越相似，其在流形上也越相近.通过最小化，就可以在低维空间得到一个足够平滑的投影，使其保持了原始空间的流形结构.因此，基于拉普拉斯正则化的似然函数可定义为式中，λ是调整算子，以调整全局信息和局部信息在似然函数中比重.通过极大化似然函数L（Θ）LapPPCA，LapPPCA的模型参数可以用EM算法估计得到.

2.2EM算法

EM算法一般通过迭代期望步（E步）和极大化步（M步）直到收敛为止.在E步，根据当前的模型参数估计隐变量的后验分布并计算似然函数；在M步，通过极大化似然函数模型参数被重新估计.在LapPPCA模型中，隐变量的期望值在E步被估计为

式中，M=PTP+σ2I.

在M步，为了极大化似然函数L（Θ）LapPPCA，需要极大化L（Θ）PPCA，并极小化.为了保证递减，本文采用了牛顿-拉松方法［11］.对于给定的f（x）和初值xt，则f（x）通过牛顿-拉松更新公式递减：

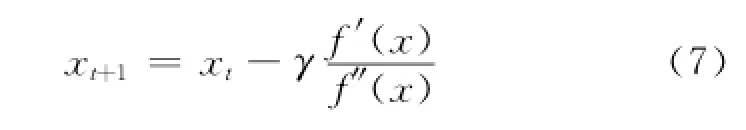
将式（7）的结果代入式（3），可得

由于图形拉普拉斯算子L是正定矩阵，故通过更新式（8）可以保证的递减.之后可以最大化似然函数L（Θ）PPCA，则模型参数更新为

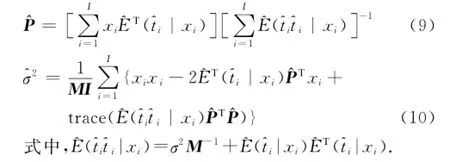
通过反复迭代E步和M步直至达到模型收敛条件可以得到最终的模型参数.由于LapPPCA通过极大化正则化的似然函数来估计模型参数，使得LapPPCA的隐变量能够同时提取数据的全局信息和局部结构，从而获取了数据更全面的特征.

2.3基于LapPPCA的过程故障检测

类似于传统的PPCA监测技术，基于LapPPCA的监测模型通过构建T2和SPE统计量来监测过程是否出现异常情况.当新的样本xnew被采集后，其对应的隐变量tnew及模型估计误差为

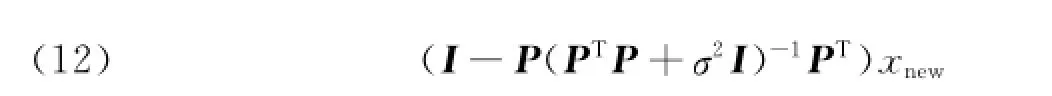
为了监测隐变量和模型残差，可以构建

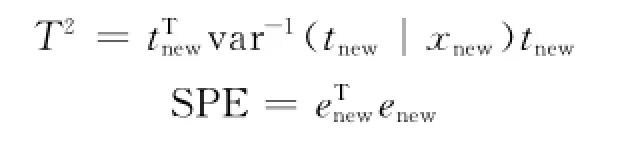
统计量来评估工业过程是否在这两个子空间下异常情况.T 2和SPE统计量的控制限服从近似的χ2分布如下［12-13］：

当新样本的T2new或SPEnew超出控制限时，则认为生产过程发生了系统故障或传感器故障，反之，则认为生产过程在平稳运行，无异常工况发生.

3　仿真研究

运用工业数据仿真平台田纳西-伊斯曼（TE）过程来检验LapPPCA的建模能力及过程监测效果. TE过程包括反应器、冷凝器、压缩机、气液分离器和解析塔等5个主要操作单元.更多TE过程的详细介绍及其控制回路设计可参考文献［14］.TE过程包含了41个过程及质量变量以及12个操作变量.本文选取了易测量的16个变量用于建模，具体变量选择参考文献［15］，选取了正常工况下500个样本点用于训练LapPPCA模型.同时，用相同的样本点训练了PPCA模型用于比较.

为了测试模型在过程监测时的有效性，选取了TE过程中21种常见的故障作为测试样本.每种故障样本均包含960个采样点，而故障均在第160个采样点发生.使用PPCA和LapPPCA模型监控所有21种故障的漏报率比较如表1所示.由表1可知，基于LapPPCA模型的T2和SPE统计量在大部分情况下都优于PPCA的故障检测效果，表中黑体标注数据为更好的监测结果.由于LapPPCA提取了数据的全局特征和局部特征，故基于隐变量构建的T2统计量能够更准确地反映过程的真实状态.与此同时，由于LapPPCA的建模精准度更高，使得模型残差部分包含的几乎都是噪声，与之对应的SPE统计量的监测效果也获得了提升.以故障10、15为例（见图1、2），基于LapPPCA模型的T2或SPE统计量的监测效果获得了比较明显的提升，而由于PPCA未能完全提取数据的全部特征，导致在监测一些微小的故障时效果不甚明显或延迟较大.

表1　PPCA和LapPPCA的漏报率比较Tab.1　Comparison of the missing detection rates of PPCA and LapPPCA

图1　故障10监测结果Fig.1　Process monitoring results of Fault 10

图2　故障15监测结果Fig.2　Process monitoring results of Fault 15

4　结　语

本文提出了一种基于LapPPCA模型，在传统的概率模型框架下，同时考虑数据的流形结构，使得在对数据进行特征提取时能够同时获取全局信息（方差）和局部信息（流形）.在LapPPCA中，通过图形拉普拉斯算子将数据的流行结构引入到似然函数中，并通过EM算法估计模型参数.同时，建立了基于LapPPCA的过程监测模型，并通过TE过程验证了所提故障检测方法的有效性.

［1］柴天佑.生产制造全流程优化控制对控制与优化理论方法的挑战［J］.自动化学报，2009，35（6）：641-649.

［2］Qin J S.Survey on data-driven industrial process monitoring and diagnosis［J］.Annual Reviews in Control，2012，36（2）：220-234.

［3］Ge Zhiqiang，Song Zhihuan，Gao Furong.Review of recent research on data-based process monitoring［J］. Industrial&Engineering Chemistry Research，2013，52（10）：3543-3562.

［4］Tipping M E，Bishop C M.Probabilistic principal component analysis［J］.Journal of the Royal Statistical Society：Series B（Statistical Methodology），1999，61（3）：611-622.

［5］Bishop C M，Nasrabadi N M.Pattern recognition and machine learning［M］.New York：Springer-Verlag，2006.

［6］Kim D，Lee I-B.Process monitoring based on probabilistic PCA［J］.Chemometrics and Intelligent Laboratory Systems，2003，67（2）：109-123.

［7］Choi S W，Martin E B，Morris J，et al.Fault detection based on a maximum-likelihood principal component analysis（PCA）mixture［J］.Industrial&Engineering Chemistry Research，2005，44（7）：2316-2327.

［8］Yu J，Qin J S.Multiway Gaussian mixture model based multiphase batch process monitoring［J］. Industrial&Engineering Chemistry Research，2009，48（18）：8585-8594.

［9］Miao Aimin，Song Zhihuan，Ge Zhiqiang，et al. Nonlinear fault detection based on locally linear embedding［J］.Journal of Control Theory and Applications，2013，11（4）：615-622.

［10］Shao Jidong，Rong Gang，Lee J M.Generalized orthogonal locality preserving projections for nonlinear fault detection and diagnosis［J］.Chemometrics and Intelligent Laboratory Systems，2009，96（1）：75-83.

［11］He Xiaofei，Cai Deng，Shao Yuanlong，et al.Laplacian regularized Gaussian mixture model for data clustering［J］.Knowledge and Data Engineering，IEEE Transactions on，2011，23（9）：1406-1418.

［12］Qin S J.Statistical process monitoring：basics and beyond［J］.Journal of Chemometrics，2003，17（8-9）：480-502.

［13］Box G E.Some theorems on quadratic forms applied in the study of analysis of variance problems，I. effect of inequality of variance in the one-way classification［J］.The Annals of Mathematical Statistics，1954，25（2）：290-302.

［14］Downs J J，Vogel E F.A plant-wide industrial process control problem［J］.Computers&Chemical Engineering，1993，17（3）：245-255.

［15］Zhou Le，Chen Junhui，Song Zhihuan，et al.Probabilistic latent variable regression model for processquality monitoring［J］.Chemical Engineering Science，2014，116（16）：296-305.

（编辑吕丹）

Laplacian Regularized PPCA for Fault Detection

ZHOU Le，SONG Zhihuan
（State Key Laboratory of Industrial Control Technology，Zhejiang University，Hangzhou 310027，China）

When the traditional probabilistic principal component analysis（PPCA）and its extended methods were used for process monitoring，the global characteristics of the process data were extracted，while，the local structure of the data was not taken into account.When the manifold was complex，the local information needed to be incorporated into the traditional model so that the model prediction could be more accurate.An Laplacian regularized PPCA（LapPPCA）model was proposed for containing both global and local information of the data.Using graph Laplacian，the manifold was introduced into the likelihood of the conventional probabilistic model and EM algorithm.The process monitoring schemes based on LapPPCA were also developed and the case study on TE benchmark indicated that the proposed method was effective for both feature extraction and fault detection.

Laplacian regularization；probabilistic principal component analysis（PPCA）based process monitoring；

TP 277

A

1671-7333（2015）03-0260-05

10.3969／j.issn.1671-7333.2015.03.010fault detection

2015-01-14

国家自然科学基金资助项目（61273167）；教育部博士学科点专项科研基金课题（20130101110138）

周乐（1987-），男，博士生，主要研究方向为基于数据驱动的故障诊断.E-mail：zjuzhoule＠zju.edu.cn

宋执环（1962-），男，教授，博士生导师，主要研究方向为复杂工程系统安全监测与故障诊断.E-mail：zhsong＠iipc.zju.edu.cn