基于约束软化的满意容错控制-输出反馈情形

张登峰1，　王执铨1，　王　宏2，　陆宝春1

基于约束软化的满意容错控制-输出反馈情形

张登峰1，王执铨1，王宏2，陆宝春1

（1.南京理工大学机械工程学院，南京210094；2.曼切斯特大学控制系统中心，曼切斯特M60 1QD，英国）

现有的满意容错控制成果难以处理非凸非线性约束，无法用于在线重构容错控制器设计，针对一类离散系统的传感器故障，研究容错系统具有上述特性的闭环区域极点指标、二次型保性能指标和控制输入等约束的满意容错控制问题.借鉴预测控制对多种约束的软化处理策略，利用被控输出反馈控制结构和在线非线性优化技术，给出一种根据故障估计信息进行递推控制的主动满意容错控制器的数值化设计算法，并分析闭环容错系统的稳定性.据此设计的满意容错控制器可使闭环容错系统在保证稳定性和控制输入约束条件下具有满意的优化性能.仿真算例验证文中设计算法的有效性.

容错控制；多目标约束；相容性分析；可行性；非线性规划

容错控制对保证现代复杂工程系统的安全可靠性具有重要意义，主动容错控制可以根据实时故障信息，在线调整控制器参数和结构，处理时变和未知故障，确保容错系统稳定和更优的性能，多年来一直是该领域的研究热点［1-2］.随着人们对控制系统性能要求的日益提高，容错系统不仅需要保证故障稳定，而且需要满足各种操作约束和其他性能要求.因此，具有多种性能约束的容错控制技术也得到关注和深入研究［3-9］.这些成果不仅保证容错控制系统的稳定性，而且强调满足其他性能约束要求.

大多数研究未明确讨论：在主动容错控制中，当既定的多种性能目标及约束条件因故障而变得不相容时，对这些约束条件和性能目标如何进行处理，使容错控制器在线重构始终具有可行解以保证容错控制的可行性.同时，现有的满意容错控制成果大多采用LMI方法设计被动容错控制器，对主动容错控制及非凸非线性的不相容约束处理很少研究［7-9］.

本文针对一类离散系统的传感器故障，借鉴模型预测控制（Model-based Predictive Control，MPC）中对约束条件的软化处理策略，采用工程上易于实现的输出反馈控制结构，给出1种基于递推控制的满意容错控制器在线重构的数值化设计算法，不仅保证故障闭环系统的稳定性，而且满足给定的控制输入约束，并具有满意的相对稳定性和优化的二次型保性能指标.仿真算例验证本文设计方法的有效性.

1　问题描述

考虑如下模型描述的一类离散系统

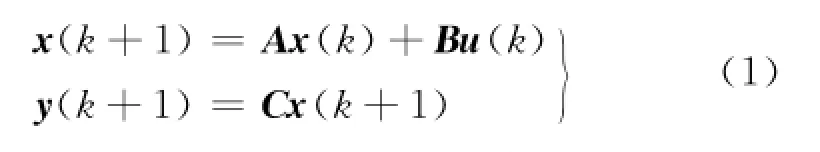
式中：k为采样时刻；x（k）∈R n是状态向量；u（k）∈R q是控制输入向量；y（k）∈R m为传感器可测量的被控输出向量；A、B和C为已知的适维定常矩阵；CTC≠0.

考虑可能的传感器故障，在系统被控输出变量y（k）与传感器输出信号ys（k）之间引入1个未知时变且有界的故障矩阵

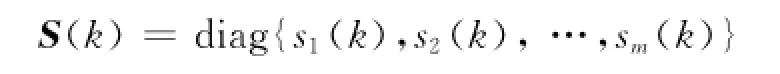
描述故障引起的传感器输入输出信号之间的偏差，其中，si（k）≠0.当si（k）=1时，表示传感器正常无故障，否则表示传感器异常故障.容错控制器采用易于实现的输出反馈控制结构，即

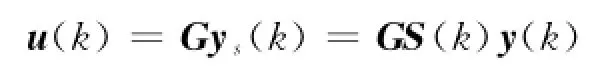
故障下的闭环容错系统模型为

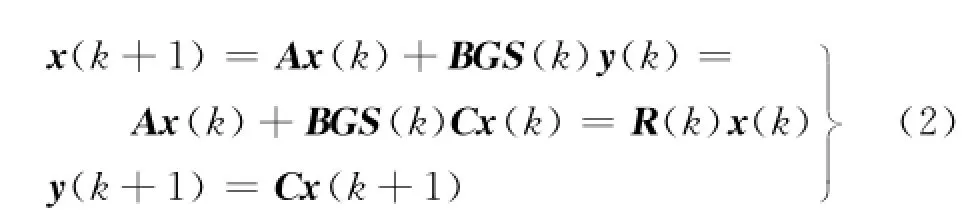
式中：G=［gij］q×m为待设计的容错控制器增益阵；R（k）=A+BGS（k）.

设计上述容错控制系统时，希望其满足以下性能和约束要求：首先，闭环系统具有一定的相对稳定性，即将闭环极点限制在单位圆内以原点为圆心、r（0＜r＜1）为半径的圆形区域Φ（0，r）内；其次，控制输入u（k）的范数不能超过给定的上界；最后，希望二次型保性能函数指标

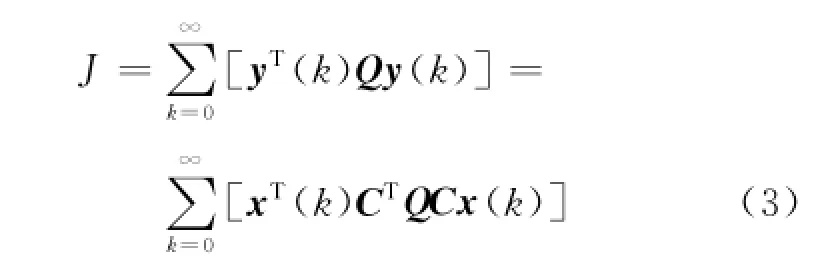
达到最优水平，其中，Q=QT＞0是给定的加权矩阵.

至此，本文的满意容错控制问题可描述为：针对系统式（1）的传感器故障，根据实时故障信息S（k），设计容错控制增益阵G，使相应的闭环系统式（2）同时满足下列约束：

（1）系统（2）的所有闭环极点位于给定的圆盘区域Φ（0，r）内，即满足Λ（R（k））Φ（0，r）.

（2）控制输入信号u（k）的2-范数满足约束

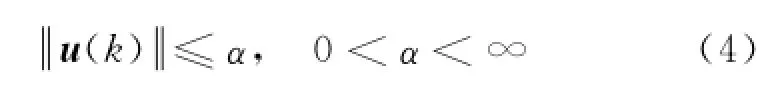
（3）闭环系统的控制性能函数（3）的上界最小化.

上述问题实质上是个有约束的多目标优化问题，称相应的可行控制器为系统式（2）的满意容错控制器［7-8］.当在线重构容错控制器时，由于事先无法准确获知实际的故障信息，正常运行时设定的各优化性能约束可能不相容，导致在线控制器重构无可行解，容错系统运行中断.因此，必须考虑容错控制器在线设计时不相容性能约束的处理策略.借鉴MPC控制对多约束的处理技术［10］，将系统的稳定性和控制输入约束（2）作为硬约束，将相对稳定性（1）的指标r和二次型性能函数（3）的上界最优化指标作为软约束.当上述指标约束不相容时，通过非线性优化技术对软约束进行松弛“软化”，使控制器设计具有满意的可行解.

2　满意容错控制器设计

为获得未知时变的故障信息，设定故障信号S（k）可由适合的在线估计方法［11］得到.容错控制器采用基于实时故障信息的逐步递推控制模式，即在每个采样时刻k，根据当前的I／O信息和故障估计值，在线设计满足当前时刻故障系统的满意容错控制器G（k）.为简化研究并不失一般性，假设系统式（1）是输出可镇定的，被控输出y（k）可检测，同时假设至少存在一个可行控制器G（k），满足系统式（2）的稳定性和硬约束（2）的要求.

2.1基于软约束松弛的满意容错控制器设计算法记当前时刻k，获知系统的状态信号x（k）、传感器输出信号ys（k）和故障实时信息S（k），并假设在第k时刻以后有

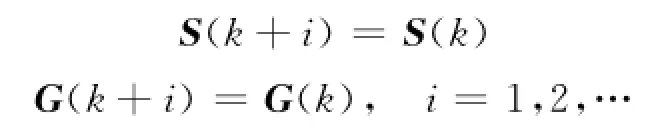
则利用第k时刻的系统信息，可预测未来时刻的控制输入、系统状态和输出信号分别为

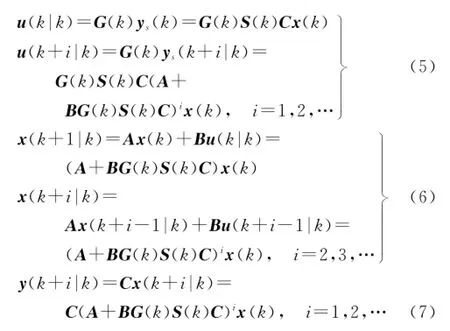
式中：u（k+i｜k），y（k+i｜k），ys（k+i｜k），x（k+i｜k）分别表示基于第k时刻的信息对未来时刻的预测.

关于二次型保性能函数指标（3），可得

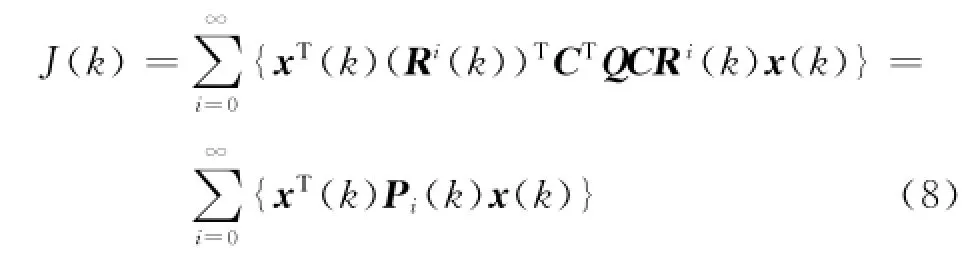
式中：

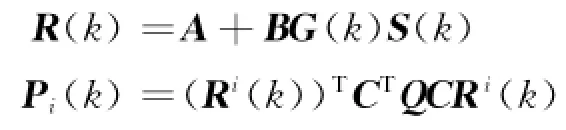
若以第k时刻为基准点，则Pi（k）的最小化意味着保性能指标式（3）的上界最优化.对Pi（k）及其矩阵迹经多次变换处理可知，当矩阵R（k）与其转置矩阵乘积的迹最小时，保性能指标式（3）的上界最优化.

考虑到未来时刻故障的未知时变性，当其变化使给定的期望性能约束（1）～（3）不相容时，采用文献［12］中的软化处理技术对其中的软约束进行松弛软化处理，使松弛后的各性能约束相容，保证控制器设计有可行解.据此，给相对稳定性约束（1）的指标r附加1个松弛变量β，得到满意容错控制器优化设计算法.

算法1在第k时刻，根据已知的系统状态信号x（k）、传感器输出信号ys（k）和故障实时信息S（k），计算带约束的优化问题

式中：δ＞0为设定的加权系数.如果上述优化问题有可行解G（k），那么该解是闭环容错系统式（2）的1个满足性能约束（1）～（3）的满意容错控制增益阵.

算法1中，优化问题式（9）的计算需满足约束式（10）中无穷多个2-范数约束条件，这在实际设计中无法实施.但根据前述的逐步递推容错控制模式，在每个时刻k仅只有控制输入u（k｜k）施于实际控制，其余预测的控制输入信号都舍弃不用.因此，算法1可简化为如下.

算法2在第k时刻，根据已知的传感器输出信号ys（k）和实时故障信息S（k），计算如下带约束的优化问题

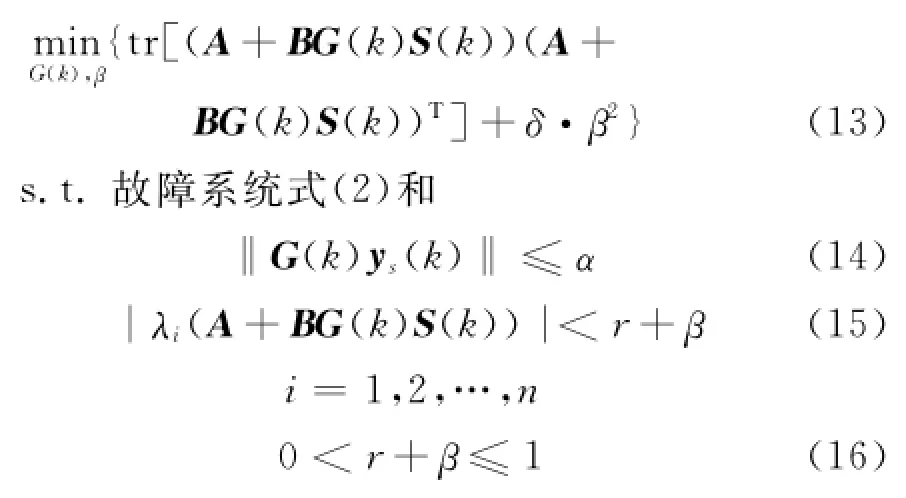
记上述优化问题可行解为｛G（k），β｝，则G（k）是闭环容错系统式（2）的1个满足性能约束（1）～（3）的满意容错控制增益阵，对应的控制输入量u（k｜k）可用于系统的容错控制.

值得注意的是，优化问题式（13）是个典型的非线性规划问题，可采用各种成熟的非线性优化算法求解，如MATLAB的fminimax和fmincon函数中的SQP、内点法与积极集法等.由于只需获得1个局部可行解就可实施有效的满意容错控制，因此可降低非线性规划问题求解的难度和复杂度.此外，系统式（1）的输出镇定与可检测性，以及满足硬约束式（4）下存在可行解等条件，保证优化问题式（13）必有可行解.

算法2通过在优化问题式（13）的目标函数中引入1个平方项δβ2，对软约束的可能违反起惩罚作用.当软约束（1）与其他性能约束不相容时，保证在获得可行解的前提下使其相应的约束违反尽可能小.当加权系数δ为0时，松弛变量β可取任意值，相当于对稳定性没有约束，系统稳定性难以保证；当加权系数δ取值越大，表示相对稳定性的要求越“硬化”，在极端情况δ→∞时，软约束指标r不允许有任何松弛，变为硬约束.因此，折中设定加权系数δ比较合理.此外，算法对二次型保性能指标上界也作软约束处理，通过优化问题可行解的变化获得满足.

2.2闭环容错控制系统的稳定性分析

满意容错控制器设计算法只能保证在采样时刻闭环容错系统式（2）的稳定性，无法确保整个容错运行过程闭环系统的稳定性［13］.因此，进一步分析闭环容错系统式（2）在数值化递推容错控制器作用下的稳定性.

定义1对于离散自治系统x（k+1）= f（x（k）），k≥0，x（0）=x0，如果对任意标量ε＞0，存在函数η=η（ε）使得下列关系成立：

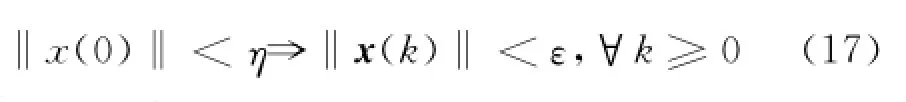
则系统的平衡点xs=0稳定［13］.

根据定义1，闭环系统式（2）的稳定性有如下定理.

定理1对传感器故障下的闭环容错系统式（2），如果在k≥kf（kf为发生故障的时刻）时带约束优化问题式（13）有可行解｛G（k），β｝，那么由时变的容错控制器序列｛G（k）：k≥kf｝构成的闭环容错系统式（2）稳定.

证明根据数值化设计算法2，利用第k时刻（k≥kf）获得的传感器输出信号ys（k）和实时故障信息S（k），得到优化问题式（13）的可行解｛G（k），β｝.根据第2.1节推导，可知该时刻下预测的最优控制输入信号u（k｜k）=G（k）ys（k）满足给定性能约束.相应地，未来时刻输出信号序列为｛y（k+ 1｜k），y（k+2｜k），…｝.由此，在第k时刻优化的二次型保性能函数式（3）

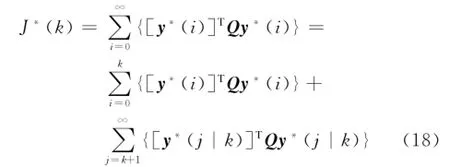
是有界的.同时，在最优控制输入u（k｜k）作用下得到预测的状态和被控输出分别为：

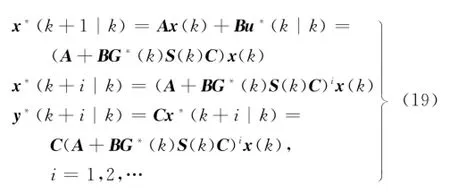
因为最优控制输入u（k｜k）使相应的闭环极点满足约束式（15），即对应的闭环系统渐近稳定，所以预测的下一时刻最优状态和被控输出满足关系式‖x（k+1｜k）‖＜‖x（k）‖和‖y（k+1｜k）‖＜‖y（k）‖.将最优控制输入u（k｜k）施加于被控对象，得到下一时刻的系统状态和被控输出为

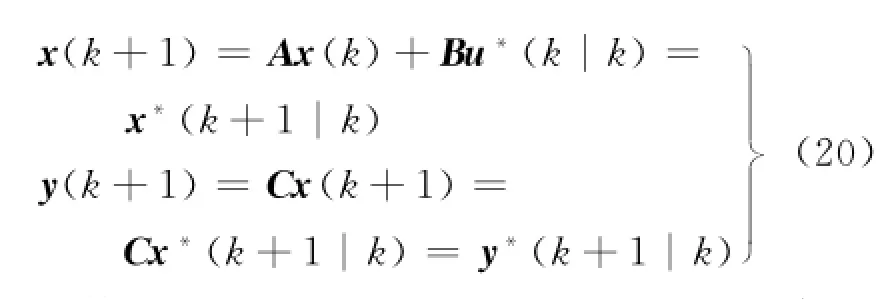
从而不等式‖x（k+1）‖＜‖x（k）‖和‖y（k+1）‖＜‖y（k）‖成立.取闭环系统式（2）的Lyapunov函数为

V（x（k））:=‖y（k）‖=‖Cx（k）‖可知随着k的增长，函数序列｛V（x（k））｝单调收敛且有下界limk→∞｛V（x（k））｝=0.

定义闭环系统式（2）平衡点附近的1个球域

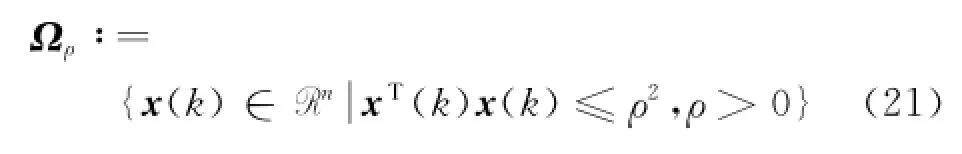
根据Lyapunov函数序列的单调收敛性，在区间（0，ρ］内必存在函数ψ1（·）和ψ2（·）满足关系式

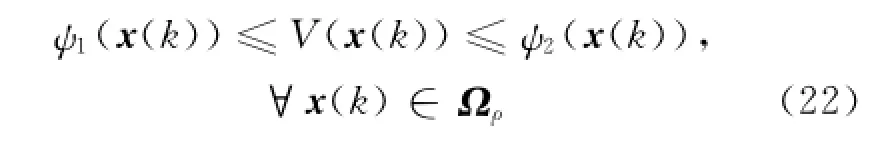
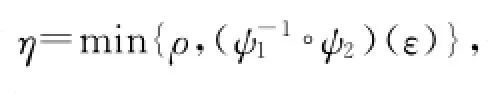
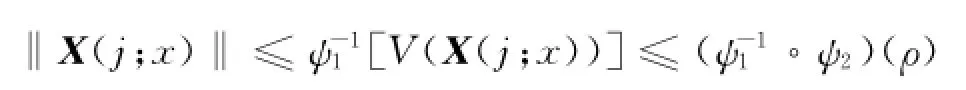
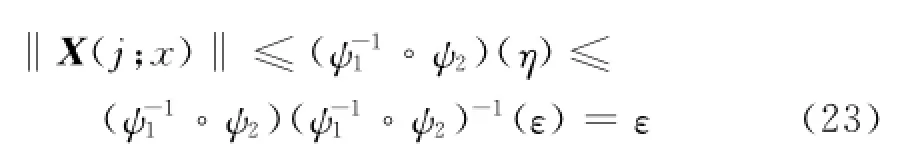
关系成立.根据定义1可知，闭环容错系统式（2）稳定.证毕.

3　仿真示例

考虑一类离散时间系统式（1）的模型参数

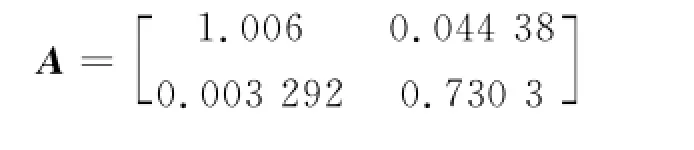
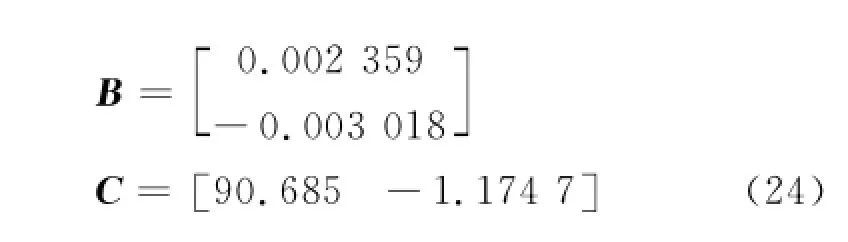
设初始状态为x（0）=［2，-1］，y（0）=182.545.传感器发生部分失效性故障，导致其输出ys（k）只有实际输出信号的50%左右，且故障估计信号也存在一定误差和随机扰动，使得到的故障估计信号见图1.设定容错系统需满足的相对稳定性指标为Φ（0，0.9），即Λ（R（k）Φ（0，0.9）；控制输入u（k）的2-范数上界约束α=50；同时使闭环系统的控制性能函数式（3）的上界最小化.

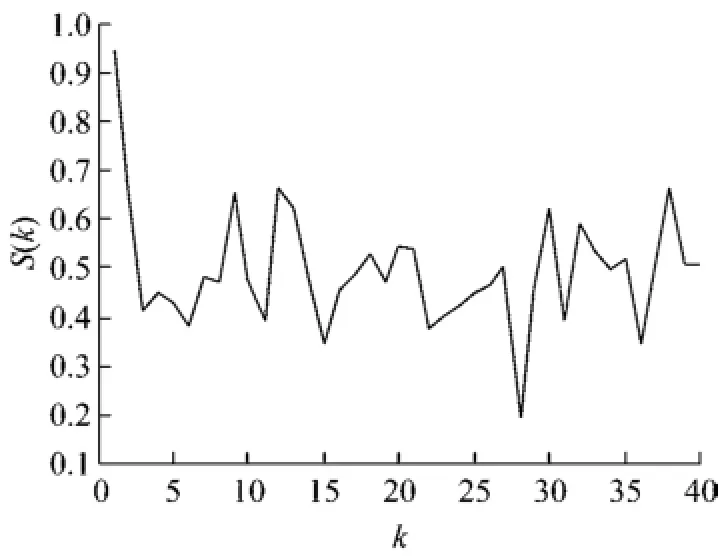
图1　估计的故障信号S（k）Fig.1　Estimated sensor fault signal S（k）

针对上述故障和性能要求，利用本文的在线滚动式主动容错控制策略，对该系统采用类似于文献［8］和［14］中的满意容错控制器LMI算法设计，计算多个LMI约束的目标优化问题时无可行解.分别采用本文有软化约束的容错控制在线设计算法（控制器记为I）和无软化约束功能的容错控制（通过将算法2中的参数β置零即可，控制器记为II），比较不同容错控制器作用下系统的零输入响应仿真结果，验证本文算法的有效性.

利用MATLAB的fmincon函数进行优化计算，图2～4分别给出了2种算法控制器作用下的控制输入幅值、闭环极点模值和被控输出响应曲线.其中，图2、3中的实线表示控制器I作用下的结果，虚线表示控制器II作用下的结果，点划线表示给定的性能约束上限.图4中的实线表示控制器I作用下的被控输出响应，虚线表示控制器I作用下故障传感器的输出；带圆圈实线表示控制器II作用下的被控输出响应，带方块实线表示控制器II作用下故障传感器的输出信号.

计算得到的控制器I作用下优化的保性能函数式（3）上界为1.44，控制器II作用下优化的保性能函数（3）上界为1.36.可见，2种容错控制方法都保证闭环容错系统的稳定性，但控制器II的控制输入幅值和闭环极点变化均违反给定“硬”约束（见图2、3（a）），多目标优化问题无可行解（根据fmincon函数功能，参数exitflag=-2表示优化问题无可行解，只给出1个使取值最大约束条件的范数最小化的伪结果），如果这种不满足硬约束的控制器施于实际对象，可能导致系统崩溃.相比之下，本文的设计算法将相对稳定性指标作为软约束处理（0＜β＜0.1，曲线见图5），使每步在线求解控制器都可行，保证闭环容错系统的安全可靠.因此，本文基于约束软化满意容错控制器设计算法有效.

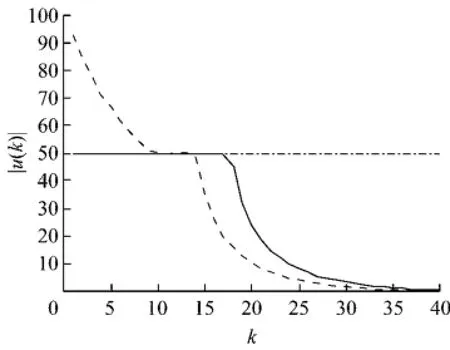
图2　控制输入信号的幅值｜u（k）｜Fig.2　Magnitude of control input｜u（k）｜

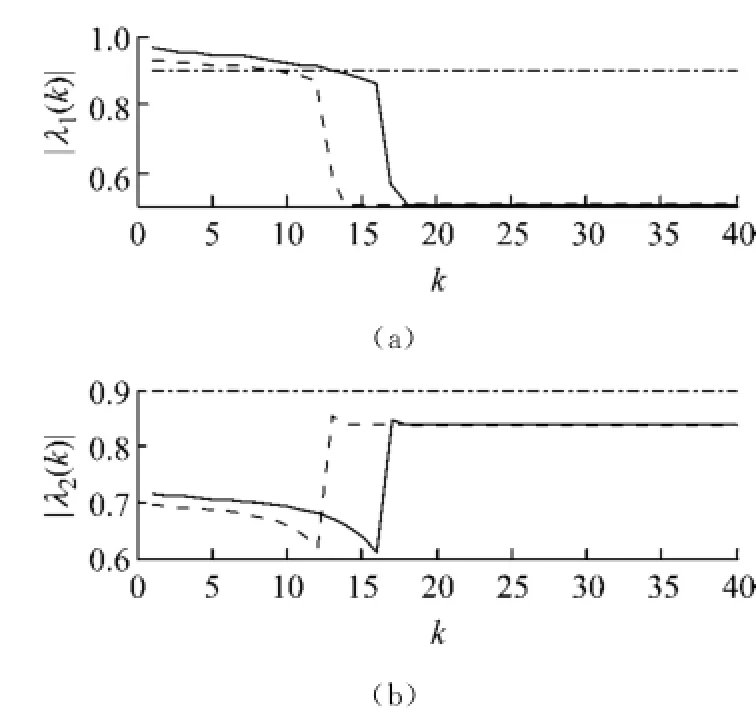
图3　闭环极点模值随时间变化曲线Fig.3　Module values of closedloop poles by time

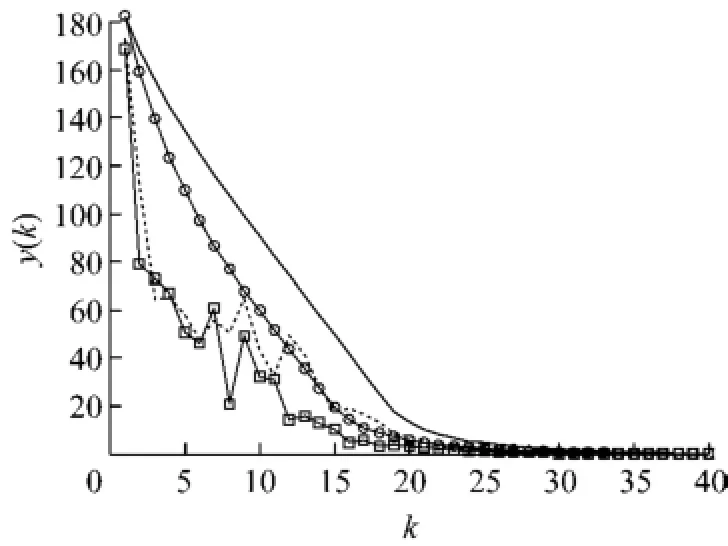
图4　故障闭环系统输出响应曲线Fig.4　Output response of the closedloop system

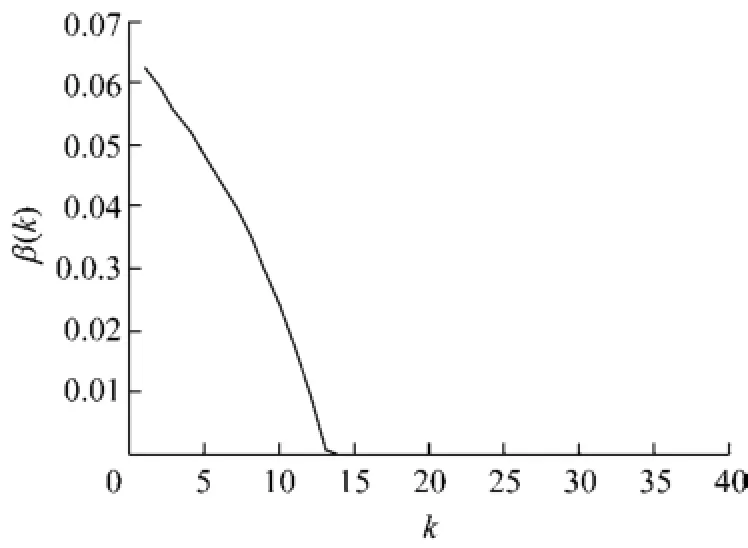
图5　有约束软化容错设计算法的参数β（k）变化曲线Fig.5　Slack factorβ（k）in the softened constraints algorithm

4　结　语

研究一类离散系统传感器故障下的满意容错控制问题.基于MPC在线滚动控制和多约束处理策略，给出1种基于约束软化处理的数值化主动容错控制器设计算法，保证闭环容错系统的稳定性和控制输入硬约束要求，同时相对稳定性和二次型保性能函数指标也得到优化.设计方法所采用的非线性多目标优化与软约束的软化技术，避免满意优化中多个非凸非线性性能约束不相容导致无可行解的难题，保证控制器在线重构设计的可行性.给出的有约束非线性优化算法在每个时刻需一步完成，当约束较多时会增加计算负担，并可能带来保守性问题.上述问题有待进一步研究.

［1］Jiang J，Yu X.Fault-tolerant control systems：a comparative study between active and passive approaches［J］.Annu Rev Contr，2012，36（1）：60-72.

［2］Wang Y Q，Zhou D H，Qin S J，et al.Active faulttolerant control for a class of nonlinear systems with sensor faults［J］.Int J Contr，Automation&Syst，2008，6（3）：339-350.

［3］Wu H N，Zhang H Y.Reliable mixed L2／H∞fuzzy static output feedback control for nonlinear systems with sensor faults［J］.Automatica，2005，41（11）：1925-1932.

［4］Pujol G，Rodellar J，Rossell J M，et al. Decentralised reliable guaranteed cost control of uncertain systems：an LMI design［J］.IET Contr Theory Application，2007，1（3）：779-785.

［5］Mhaskar P，Gani A，Christofides P D.Fault-tolerant control of nonlinear processes：performance-based reconfiguration and robustness［C］／／Proc 2006 Am Contr Conf.Minneapolis USA，2006：6020-6025.

［6］Dominguez-Garcia A D，Kassakian J G，Schindall J E，et al.An integrated methodology for the dynamic performance and reliability evaluation of fault-tolerant systems［J］.Reliability Eng&Syst Safety，2008，93 （11）：1628-1649.

［7］Zhang D，Wang Z，Hu S.Robust satisfactory faulttolerant control of uncertain linear discrete-time systems：an LMI approach［J］.Int J Syst Sci，2007，37（2）：151-165.

［8］张登峰，王执铨，韩笑冬.满意容错控制［M］.北京：科学出版社，2014.

［9］Zhang D，Su H，Chu J，et al.LMI approach to reliable guaranteed cost control with multiple criteria constraints：the actuator faults case［J］.Int J Robust Nonlinear Contr，2009，19（8）：884-899.

［10］Maciejowski J M.Predictive control with constraints ［M］.Harlow：Pearson Education Limited，2002.

［11］Zhang K，Jiang B，Shi P.Observer-based fault estimation and accomodation for dynamic systems ［M］.Berlin：Springer-Verlag，2012.

［12］Zheng A，Morari M.Stability of model predictive control with mixed constraints［J］.IEEE Trans Automatic Contr，1995，40（10）：1818-1823.

［13］陈虹.模型预测控制［M］.北京：科学出版社，2013.

［14］Zhang D，Wang H，Lu B.Static output feedback reliable controller design of nonlinear systems with multiple constraints［C］／／Proc 12th Int Conf Contr，Automation，Robotics&Vision.Guangzhou，2012：498-503.

（编辑俞红卫）

Satisfactory FaultTolerant Control with Soften ConstraintsOutput Feedback Case

ZHANG Dengfeng1，WANG Zhiquan1，WANG Hong2，LU Baochun1
（1.School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China；2.Control Systems Centre，University of Manchester，Manchester M60 1QD，UK）

In view of the difficulty for the existing satisfactory fault-tolerant control in dealing with nonlinear and non-convex constraints，it is not appealing to the online reconfiguration of active faulttolerant control.Hence，the active satisfactory fault-tolerant control was studied for a class of discretetime systems subject to sensor faults.The study involved the non-convex and nonlinear performance constraints on regional closed-loop poles，quadratic guaranteed performance and control input.Referring to the constraints softening technique in predictive control，a numerical algorithm was developed for the faulttolerant controller reconfiguration by using online nonlinear programming.The time-varying controller with static-output feedback structure was designed from the estimated fault information，which regulated the faulty system in the moving horizon way.The stability of the closed-loop system was also analyzed. Thus，the satisfactory multiple performance of the resulted fault-tolerant system was guaranteed.A numerical example was illustrated to indicate the validity of our proposed method.

fault-tolerant control；multi-objective constraints；consistency analysis；feasibility；nonlinear programming

TP 13；TP 273

A

1671-7333（2015）03-0305-06

10.3969／j.issn.1671-7333.2015.03.018

2015-01-13

国家自然科学基金资助项目（61374133，60804027，51275245）；江苏省“六大人才高峰计划”项目（2011-ZBZZ-011）；江苏省高校优势学科建设工程项目（PAPD）

张登峰（1973-），男，副教授，博士，主要研究方向为故障诊断与容错控制.E-mail：mydfzhang＠qq.com