基于有效分类的多模态过程故障检测及应用

尤　博，　彭开香

基于有效分类的多模态过程故障检测及应用

尤博，彭开香

（北京科技大学自动化学院，北京100083）

多模态的故障检测作为复杂的实际问题，得到越来越多的重视.围绕多模态的故障检测问题展开相应关键问题研究，首先提出一种基于K均值聚类算法结合聚类有效性指标求解出最佳模态数方法，通过数值仿真和带钢热连轧生产过程数据进行验证；然后利用模糊C均值算法对训练数据进行模态划分，针对不同模态，利用主成分回归方法建立相应的监测模型，实现对故障的有效检测；最后将该故障检测方法应用到带钢热连轧生产过程.仿真结果表明，不仅实现合理模态划分和识别，而且取得良好的检测效果.

故障检测；多模态；模态划分；模态识别；带钢热连轧

随着现代工业的快速发展，原材料的波动、工作点的调整、产品规格及批次不同等使生产过程的工况频繁发生改变.这种多工况特性使得1个连续生产过程经常在不同模态间转换，对于这些包含多个操作模态的生产过程，传统的故障检测方法（如主元分析（PCA）、偏最小二乘（PLS）等算法）很难直接应用.这些算法往往针对具有1个稳定状态的过程进行处理，将传统方法应用到这些过程时会出现问题.

复杂生产过程的多工况特性决定其本身呈现出不同的生产模态，不同模态往往具有不同的数据特征.如果用1个模型监测不同的模态，很难起到良好的故障检测效果.Zhao等［1-2］通过多向PCA和PLS方法对多模态过程进行故障检测，对于不同模态，多向PLS模型的建立依据不同模型之间的角度度量，这个角度可衡量任意2个PLS模型的相似度.文献［3］中从不同阶段划分出发，对不同阶段分别进行故障检测.在多模态问题处理中，针对不同的操作模态，训练数据被划分成不同类别，进而建立相应的模型，使故障检测更具有针对性.此外，混合高斯模型（GMM）也被广泛应用到多模态的故障检测中［4-8］. Yu等［4］提出一种新的方法，将有限混合高斯模型与贝叶斯策略结合，进行故障检测.GMM方法可以将具有相似特征的数据划分为同一类，不同类别的数据集合具有不同的均值和协方差.通过GMM划分，每个类别都可看作是服从一个特定的高斯分布.在这些处理方法中，没有明确给出如何确定多模态的最佳模态数.

在对多模态问题的处理过程中，训练数据的合理聚类即确定出最佳模态数，对于后续的故障检测至关重要.常用的聚类方法有K均值算法（K-means）、GMM、模糊C均值（FCM）聚类等，这些方法需预先给定聚类数才能对训练数据进行聚类分析.本文在确定最佳聚类数时，首先针对训练数据确定聚类数搜索范围，通常情况下最小聚类数为2，最大聚类数根据具体情况确定.运行聚类算法，产生不同聚类数目的聚类结果，选择合适的有效性指标对聚类结果进行评估，由评估结果确定最佳聚类数.

作为聚类分析中使用最广泛的算法之一，K-means聚类算法对大型数据集的处理效率较高，特别是当样本分布呈现类内团聚状时，可达到较好的聚类结果.本文以K-means聚类算法为基础，从距离测度考虑，引入一种基于样本几何结构的聚类有效性指标——类间类内划分（Between-Within Proportion，BWP）指标［9］.在此基础上形成1种确定K-means算法最佳聚类数的算法，并通过数值仿真和实际的带钢热连轧生产过程数据进行验证.在确定最佳聚类数后，利用FCM聚类结合最佳聚类数对训练数据进行模糊划分，确定不同模态，进而建立不同模态下的检测模型.利用主成分回归（Principal Component Regression，PCR）方法［10］，通过贝叶斯分类能力实现对轧钢生产过程的故障检测.

1　多模态最佳聚类数确定及聚类方法

1.1基于BWP指标确定最佳聚类数

1.1.1BWP聚类有效性指标

评价聚类结果优劣的过程称为聚类有效性分析，在引出BWP指标前先定义几个概念.

定义1令R为聚类空间，X=｛x1，x2，…，xn｝，假设n个样本对象被聚类为k类，定义第j类的第i个样本的最小类间距离b（j，i）为该样本到其他每个类中样本平均距离的最小值，即

定义2令R为聚类空间，X=｛x1，x2，…，xn｝，假设n个样本对象被聚类为k类，定义第j类的第i个样本的类内距离w（j，i）为该样本到第j类中其他所有样本的平均距离，即

在确定聚类有效性时，希望最终聚类结果类内紧密、类间远离.从类内紧密角度考虑，样本的类内距离w（j，i）越小越好；从类间远离角度考虑，样本离近邻聚类的距离及最小类间距离b（j，i）越大越好.综合考虑这2种因素，并且使指标不受量纲影响，可引入对BWP指标的定义.

定义3令R为聚类空间，其中X=｛x1，x2，…，xn｝，假设n个样本对象被聚类为k类，定义第j类的第i个样本的BWP指标［9］为

由式（3）可知，当样本的类内距离与样本的最小类间距离相比可忽略时，BWP指标的值近似为1，说明此时该样本被正确聚类；当样本的最小类间距离与样本的类内距离相比可忽略时，BWP指标的值近似为-1，说明此时该样本被错误聚类.BWP指标反映单个样本的聚类有效性情况，指标值越大，说明单个样本的聚类效果越好.通过求某个数据集中所有样本的BWP指标值的平均值，分析该数据集的聚类效果.显然，平均值越大，该数据集的聚类效果越好，其最大值所对应的聚类数为最佳聚类数，由此可得：

式中：avg BWP（k）表示数据集聚成k类时的平均BWP指标值；kopt表示最佳聚类数.

1.1.2基于K-means的最佳聚类数方法

通过以上分析，将K-means算法与BWP聚类有效性指标结合起来，提出一种分析聚类效果，确定最佳聚类数的算法.算法归纳如下：

（1）选择聚类数的搜索范围［kmin，kmax］.

（2）从kmin开始，到kmax结束，①调用K-means算法；②计算单个样本的BWP指标值；③计算平均BWP指标值.

（3）计算得出最佳聚类数.

（4）输出最佳聚类数、有效性指标值和聚类结果等.

1.2FCM聚类算法描述

FCM是一种用隶属度确定每个数据点属于某个聚类程度的聚类算法.FCM把n个样本

X=｛x1，x2，…，xn｝

分成c个模糊组，并求每组的聚类中心，使得非相似性指标的目标函数达到最小.隶属度矩阵U的取值为［0，1］的元素.在归一化条件约束下，1个数据集的隶属度和总等于1，即

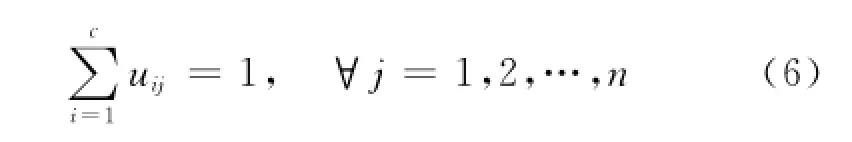
FCM的目标函数为

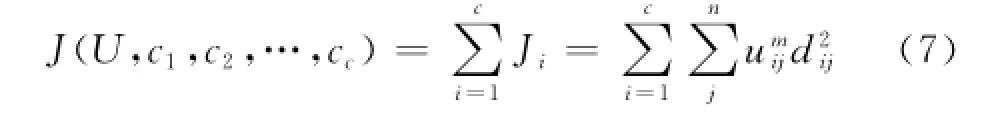
式中：uij取值为［0，1］；ci为模糊组i的聚类中心；dij=‖ci-xj‖为第i个聚类中心与第j个数据点间的欧式距离；m∈［1，∞）是加权指数.

为得到数据集合的最佳模糊划分，需求min｛J（U，c1，c2，…，cc）｝.为此，构造新的目标函数

式中：λj（j=1，2，…，n）是式（6）n个约束式的拉格朗日乘子.对所有输入参量求导，使式（7）达到最小的必要条件为

和

通过上述分析，可归纳出FCM在确定聚类中心ci和隶属度矩阵U时的算法：

（1）用值在0～1的随机数初始化隶属矩阵U，使其满足式（6）中的约束条件；

（2）用式（9）计算c个聚类中心ci，i=1，2，…，c；

（3）根据式（7）计算目标函数，如果小于某个确定的阈值，或相对上次目标函数值的改变量小于某个阈值，则算法停止；

（4）用式（10）计算新的U矩阵.返回步骤（2）.

最终进行模态划分时采取FCM.原因是K-means算法是一种硬聚类算法，某个样本确切地属于某类，非此即彼；而FCM算法则是一种柔性的模糊划分，利用隶属度确定每个样本属于某个聚类的程度.最后根据隶属度矩阵，按照模糊集合中最大隶属原则确定每个样本的分类，使聚类结果更加准确.尤其针对带钢热连轧这种复杂的间歇过程，不同模态之间的过渡过程会使过程数据呈现出更多的不确定性.通过这种模糊方法，可以尽量减少对监测精度的影响.

2　多模态建模与故障检测

2.1基于PCR的建模

在确定好分类数，合理将数据分类后，针对每类数据，利用文献［10］中提出的PCR方法对过程变量X和质量变量Y分别建模.相对传统的PLS，PCR在得出相似结果的前提下，计算量大大减少.

PCR算法的基本步骤如下：

（1）对过程变量X进行PCA分解，可以得到X=^X+~X=TpcP Tpc+TresPTres；

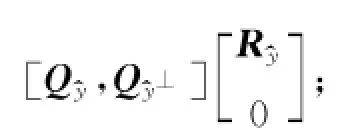
（5）对子空间Xy^和Xy^⊥分别进行PCA分解，得到

该方法将过程变量X分解为3个子空间，2个子空间与质量相关.为实现故障检测的目的，采用传统的T 2统计量和SPE统计量.3个不同子空间的统计量分别为：

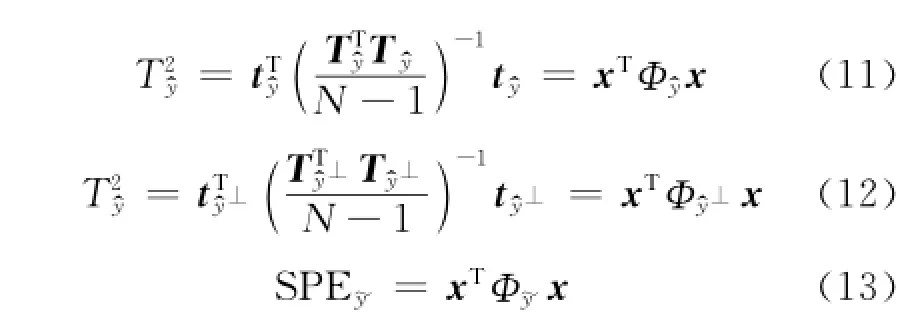
2.2基于贝叶斯的分类

当有新的数据xnew时，首先需要将其归到相应的类中，才能利用相应的模型进行故障检测，本文主要利用贝叶斯分类能力.假设训练数据被分为k类，利用PCR算法可以产生k个模型，每个模型都有相应的线性回归系.对于新数据xnew，首先利通用过相应的均值和协方差信息对数据进行归一化，通过

可得到相应的预测质量变量.

定义先验概率公式为

式（15）给出xnew属于第i类的先验概率，i=1，2，…，k.其中y（i）j 代表第i类训练数据的第j个样本，y^（i）j 代表第i类训练数据第j个样本的预测值.

根据贝叶斯公式，后验概率为

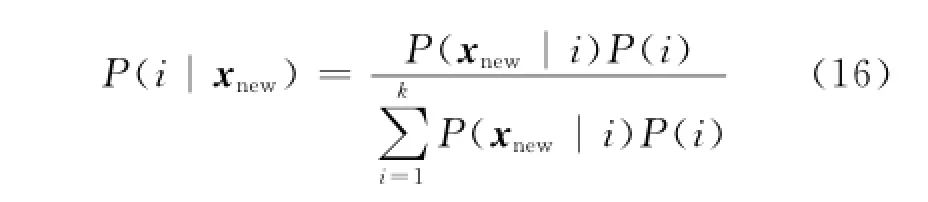
式中：

当某类对应的后验概率最大时，xnew便属于那一类，即

2.3多模态过程故障检测

在处理多模态过程的故障检测问题中，首先对训练数据进行合理划分；在此基础上，针对不同模态建立相应模型；当检测数据出现时，利用贝叶斯的分类能力将数据划分到对应的模型中，进行合理的故障检测.多模态过程故障检测流程见图1.

图1　多模态过程故障检测流程Fig.1　The flow chart of multimode process fault detection

3　仿真分析

3.1最佳模态数确定

为验证最佳聚类数的选取，首先考虑1个数值案例.随机产生3组样本数为100，维数为3的高斯分布.第1组avg 1=［0 0 0］，cov 1=［0.3 0 0；0 0.35 0；0 0 0.3］；第2组avg 2=［1.25 1.25 1.25］，cov 2=［0.3 0 0；0 0.35 0；0 0 0.3］；第3组avg 3= ［-1.25 1.25-1.25］，cov 3=［0.3 0 0；0 0.35 0；0 0 0.3］.其中，avg表示均值，cov表示协方差.3组数据共同组成训练数据集X.

将kmax设定为4，利用本文方法确定最佳聚类数，最终结果如表1所示.

表1　不同分类数的BWP指标值Tab.1　BWP index of different categories

训练数据分布及不同分类数的数据分布情况如图2～5所示.可知，当训练数据集被分成3类时，BWP值最大，仿真图也与训练数据的分布最接近.

以实际的带钢热连轧生产过程为研究对象.轧钢过程本身是个多模态过程，在不同操作模态下生成的数据具有不同的均值、协方差等统计特性.在整个生产过程中，往往更关心最终的输出，即质量变量，如厚度、平直度等.因此，在质量变量相关的情况下对过程变量进行划分，对不同的模态进行建模监测很有必要.

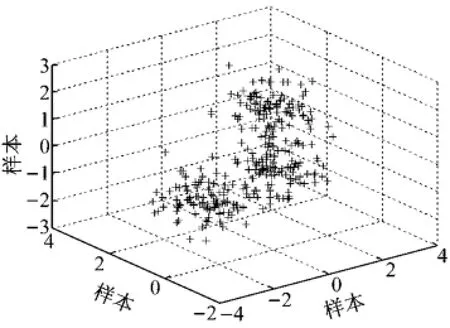
图2　训练数据分布Fig.2　Distribution of training data

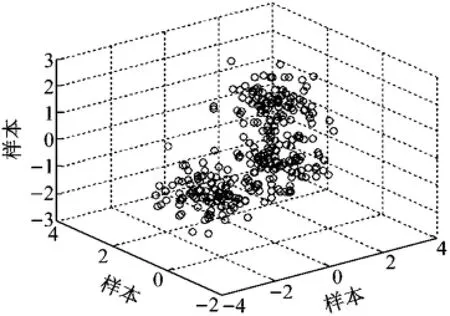
图3　2类数据分布Fig.3　Distribution of two kinds of data

图4　3类数据分布Fig.4　Distribution of three kinds of data

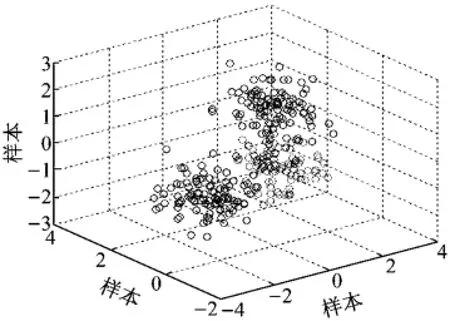
图5　4类数据分布Fig.5　Distribution of four kinds of data

在考虑输出y进行聚类时，一般有2种方法：①将输入x和输出y合并成1个新的向量，即z=（x，w y），对z运用某种聚类方法进行划分，其中，w表示输出的权重，是个经验值，代表输出y对于聚类的影响程度［11］；②将输出y看作是对输入x聚类时的一种约束，就像是一种附加条件，首先根据输出y进行粗略划分，在此基础上对输入x采取相应的聚类方法进行划分，从而得出最终的聚类结果.

以轧钢出口厚度为质量变量，选取目标厚度值分别为1.82，2.69，3.95这3类数据.正常情况下，实际出口厚度值会在目标厚度值附近浮动，因此通过对质量变量出口厚度的判断分析，可选取kmax= 3，利用本文方法得到结果见表2.可知，当分成3类时BWP值最大，是最佳分类数，验证选取的3类数据分类的有效性.

表2　不同分类数的BWP指标值Tab.2　BWP index of different categories

3.2轧钢过程的故障检测

以轧钢数据为基础，3种厚度数据共同组成训练数据，再选取1组故障数据，出口厚度目标值为3.95.发生故障的样本范围为1 270～2 280.通过FCM算法对训练数据分类后，可以得到3类数据，将出口厚度目标值为1.82看作是第1类数据，将出口厚度目标值为2.69看作是第2类数据，将出口厚度目标值为3.95看作是第3类数据.当出口厚度目标值为3.95的故障数据出现时，其在不同类下的贝叶斯分类结果如图6所示.

图6　不同类下新样本的先验概率Fig.6　The prior probability of the new samples under different categories

由图可知，故障数据的确对应于第3类训练数据的类型，其对应的第1、第2类训练数据的先验概率均为0.因此，可以用第3类训练数据建好的模型进行故障检测.仿真结果见图7.为说明处理多模态问题分类的重要性，在不分类的情况下给出相应的故障检测仿真结果，如图8所示.

图7　主元空间和与质量相关的残差空间仿真Fig.7　The simulation diagram of main subspace and qualityrelevant residual subspace

图8　不分类情况下主元空间和与质量相关的残差空间仿真Fig.8　The simulation diagram of main subspace and qualityrelevant residual subspace without classification

4　结　语

在处理多模态问题的故障检测时，给出明确的模态划分指标.仿真案例说明，该指标可很好地按照欧式距离对训练数据进行合理划分.模态的合理划分为后续故障检测奠定基础.通过PCR与贝叶斯公式的结合，新的数据被识别到相应模态中，通过已有监测模型进行有效的故障检测.将该方法应用到带钢热连轧过程中，得到良好的模态划分、识别与故障检测效果.

［1］Zhao SJ，Zhang J，Xu Y M.Monitoring of processes with multiple operating modes through multiple principal component analysis models［J］.Ind Eng Chem Res，2004，43（22）：7025-7035.

［2］Zhao SJ，Zhang J，Xu Y M.Performance monitoring of processes with multiple operating modes through multiple PLS models［J］.J Process Contr，2006，16 （7）：763-772.

［3］Doan X T，Srinivasan R.Online monitoring of multiphase batch processes using phase-based multivariate statistical process control［J］.Computers Chem Eng，2008，32（1-2）：230-243.

［4］Yu J，Qin S J.Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models［J］.AIChE J，2008，54（7）：1811-1829.

［5］Yu J，Qin S J.Multiway Gaussian mixture model based multiphase batch process monitoring［J］.Ind Eng Chem Res，2009，48（18）：8585-8594.

［6］许仙珍，谢磊，王树青.基于PCA混合模型的多工况过程监控［J］.化工学报，2011，62（3）：743-752.

［7］Choi S W，Park J H，Lee I B.Process monitoring using a Gaussian mixture model via principal component analysis and discriminant analysis［J］.Computers Chem Eng，2004，28（8）：1377-1387.

［8］Yuan X F，Ge Z Q，Song Z H.Soft sensor model development in multiphase／multimode processes based on Gaussian mixture regression［J］.Chemometrics& Intelligent Laboratory Systems，2014，138（1）：97-109.

［9］周世兵.聚类分析中的最佳聚类数确定方法研究及应用［D］.无锡：江南大学，2011.

［10］Peng K X，Zhang K，Dong J，et al.Quality-relevant fault detection and diagnosis for hot strip mill process with multi-specification and multi-batch measurements［J］.J Franklin Inst，2014，352（2）：987-1006.

［11］Wang D，Zeng X J，Keane J A.An input-output clustering method for fuzzy system identification ［C］／／Fuzzy Systems Conf.London，2007：1-6.

（编辑俞红卫）

Fault Detection and Application Based on the Effective Classification for Multimode Processes

YOU Bo，PENG Kaixiang
（School of Automation and Electrical Engineering，University of Science and Technology of Beijing，Beijing 100083，China）

Multimode process fault detection，a complicated practical problem，has attracted increasing attention.Some key issues in multimode process fault detection were researched.Firstly，a way to solve the optimal mode number based on K-means clustering algorithm combining with clustering validity index was put forward，which was verified by numerical simulation and the data of hot strip mill process.Then，the fuzzy C-means algorithm was utilized to classify the training data.According to different modes，the principal component regression method was employed to establish the corresponding monitoring models，in order to implement effective fault monitoring.At last，the fault detection method was applied in hot strip mill process.The simulation results showed that it could not only realize the reasonable mode classification and recognition，but also achieve good detection effect.

fault detection；multimode；mode classification；mode recognition；hot strip mill

TP 273

A

1671-7333（2015）03-0242-06

10.3969／j.issn.1671-7333.2015.03.007

2015-01-12

尤博（1990-），男，硕士生，主要研究方向为间歇过程监测与故障诊断.E-mail：yb-0520＠163.com

彭开香（1971-），男，教授，博士生导师，主要研究方向为统计过程监测与故障诊断、复杂工业系统的建模与控制. E-mail：kaixiang＠ustb.edu.cn