一种1T2R卧式布局并联机构的重力补偿策略

宋轶民，王晓莉，连宾宾，孙 涛

(天津大学机构理论与装备设计教育部重点实验室，天津 300072)

与串联机构相比，并联机构在刚度、精度、静/动态特性等诸多方面具有潜在优势[1]．以并联机构为主体搭建的加工装备已被公认为是零部件高质量加工装备的优势解决方案[2-5]．西方发达国家在飞机机翼等超大型部件加工中应用的 Tricept及 Ecospeed即是该方案的典型代表[6-7]．

考虑到待加工零部件的尺寸及并联机构与超长行程导轨单元集成的难易程度，并联机构一般被设计为卧式布局．与立式布局相比，卧式布局的并联机构受自身重力影响较大，为平衡自重，驱动电机将增大输出功率，增加成本的同时也会缩短电机的使用寿命. 此外，自重将导致卧式并联机构的运动部件产生变形，影响加工精度．因此，研究卧式布局并联机构的重力补偿策略对提高机构性能具有极为重要的理论意义和工程实用价值．

目前，普遍采用的机构重力补偿策略有受控力平衡与结构设计自平衡两种形式．受控力平衡主要以气、液压缸及电机等为补偿力源直接补偿机构重力．孟祥志等[8]采用液压缸为主要施力源，辅以弹簧组及凸轮机构来实现 3-UPS并联机构(U、P及 S分别代表虎克铰链、移动副和球铰链)的重力补偿，通过优化补偿装置的相关参数，显著降低了驱动电机用于平衡自重的输出功率；陈有清[9]以3-(2SPS)并联机构为研究对象，提出了一种基于比例缩放仪的重力补偿装置．研究表明，采用受控力平衡形式的重力补偿策略易于根据负载变化实现重力补偿，然而，当机构运动速度、加速度较大时，液压缸易出现冲击、驱动过载等问题，而气压装置的体积较大并伴有严重的排气噪声，且该类补偿装置结构复杂、设计成本高，应用范围受限[10]．

通过结构设计保持机构质心不变，是实现机构重力补偿的另一策略．Gosselin等[11-12]借助配重法，研究了四、六自由度并联机构的重力补偿问题，得到了适用于机构重力补偿的质量分配条件．Russo等[13]、孟祥志等[14]分别以六自由度和三自由度并联机构为研究对象，利用配重法实现了其重力补偿，并提出了利用比例缩放机构实现机构重力补偿的解决方案．然而，配重会增大机构运动部件的质量和系统惯性，降低系统固有频率，从而影响机构的动态特性．

添加弹簧等储能元件，使机构总势能保持恒定，亦可达到机构重力补偿的目的．Ebert-Uphoff等[15]、何雷等[16]提出了添加零初长弹簧及合理设计杆组结构参数的方法，并据此完成了6-RRS(R代表转动)并联机构及一种空间机械臂的重力补偿，然而，零初长弹簧由一般弹簧、滑轮和钢丝绳组成，增加了机构的复杂程度，且易使机构发生干涉；吴孟丽等[17]利用机械拉伸弹簧及辅助杆平衡装置，实现了 TAM 机构的重力补偿，大幅度降低了用于平衡重力的驱动力，补偿效果明显；Dehkordi等[18]以 3-UPU 并联机构为研究对象，通过在重力方向悬吊安装机械拉伸弹簧组来补偿机构重力，且辅以沿机构移动副方向的压缩弹簧来减小电机的驱动功率．然而，压缩弹簧会阻碍支链的回程运动，电机需增大输出功率来克服弹簧阻力．

综上所述，不难发现添加弹簧等储能元件保持机构总势能不变，是机构重力补偿的优势解决方案．然而，如何有效添加弹簧等储能元件，不增加机构复杂程度，不干涉机构运动，合理优化弹簧等储能元件的安装位置与相关参数，及保持在整个工作空间内的补偿效果，值得深入研究．

本文以可实现 1T2R(T代表移动)三自由度运动的3-RPS卧式并联机构为例，借助添加弹簧元件的方法，研究该机构的重力补偿问题．首先，求解 3-RPS机构的运动学，并据此构建机构的重力补偿模型；其次，采用遗传算法，实现弹簧安装位置及弹性系数等变量的优化设计；最后，建立计及重力的机构柔度模型，评估及校核重力补偿效果．

1 机构简介与逆位置分析

如图 1所示，3-RPS并联机构由静平台、动平台及连接两者的 3条 RPS支链组成，P,表示主动移动副．3条RPS支链具有相同的拓扑结构且呈轴对称分布．在3条RP S支链相互配合下，动平台可实现两维转动和一维移动，即1T2R运动．

图1 以3-RPS卧式布局并联机构为主体搭建的加工装备Fig.1 Processing equipment based on 3-RPSparallel manipulator with horizontal layout

3-RPS并联机构的结构简图如图2所示．点Bi、Ai(i＝1，2，3)分别表示机构第i条支链的转动副和球铰副中心．不失一般性，△B1B2B3、△A1A2A3是以 O、P为几何中心，b、a为外接圆半径的 2个正三角形，分别作为机构的静、动平台平面．为描述机构动平台的运动，需建立如下坐标系．以O为坐标原点建立固定坐标系 Oxyz，其中 x轴与B2B3平行，z轴与静平台平面垂直，y轴满足右手定则；以 P为坐标原点建立动平台连体坐标系 Puvw，初始姿态下各轴方向与Oxyz平行；以 Bi为坐标原点建立支链固定坐标系Bixiyizi和支链连体坐标系 Biuiviwi(i＝1，2，3)，各轴线方向如图2所示．

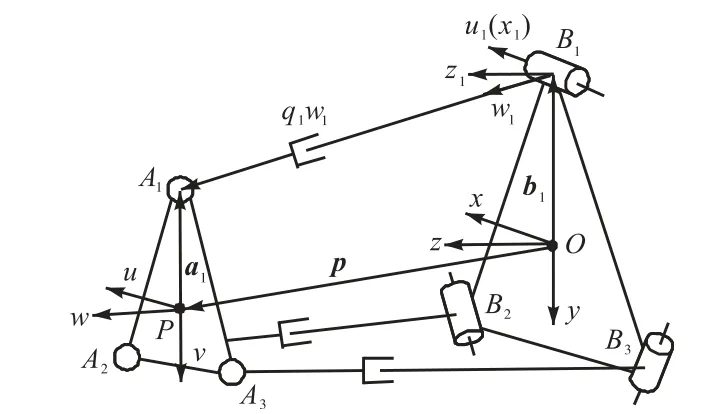
图2 3-RPS卧式布局并联机构的结构示意Fig.2 Schematic diagram of 3-RPS parallel manipulator with horizontal layout

如图 3所示，系 Puvw相对系 Oxyz的姿态矩阵的欧拉角变换可表示为

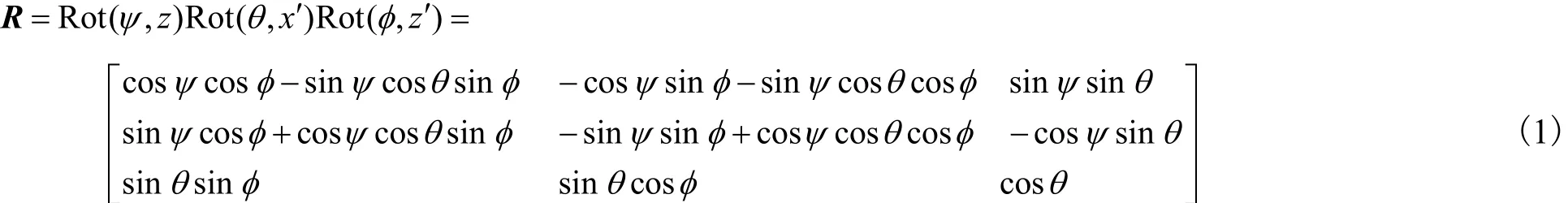
式中ψ、θ、φ 分别为进动角、章动角及自旋角．

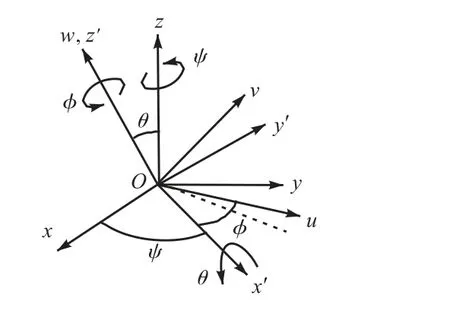
图3 欧拉角示意Fig.3 Definition of the Euler angles

动平台中心点P在系Oxyz中的位置矢量可表示为p = (x yz )T，构造机构的闭环矢量约束方程为

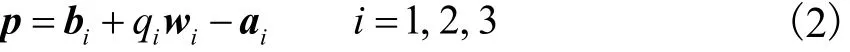
式中：qi、wi分别为 RP S支链的伸长量和轴向单位矢量；bi、ai分别为点 Bi、Ai在系 Oxyz中的位置矢量，且

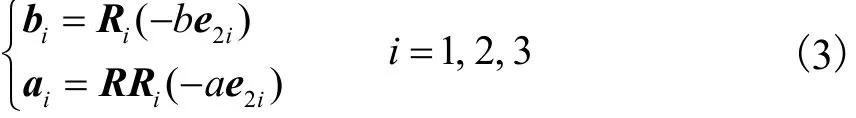
式中：e2i为沿 yi轴的单位矢量；Ri为系 Bixiyizi相对于系Oxyz的旋转矩阵．

如图2所示，支链i中转动副限制了点Ai沿xi轴的移动，故可构造约束方程

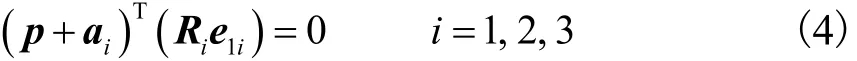
式中e1i为沿xi轴的单位矢量．

联立式(1)～式(4)，可得机构的位置逆解为

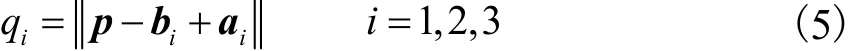
为更好地描述机构的运动特性，以式(1)中所述ψ、θ为自变量，得

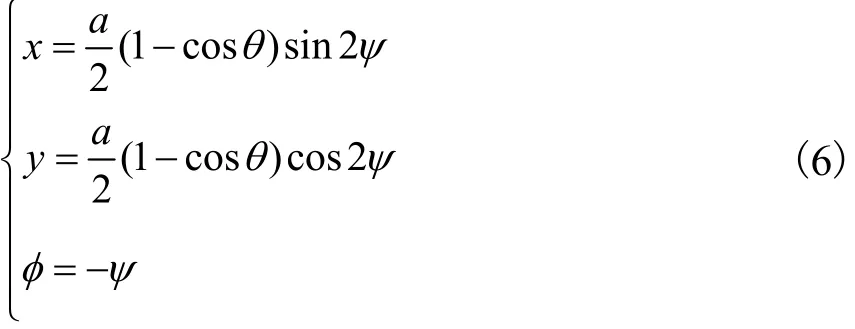
因此，将式(6)代入式(5)可得以 ψ、θ及 z为输

出广义坐标的机构位置逆解．

2 重力补偿

2.1 重力补偿策略

基于上述原理，通过添加弹簧等储能元件，使 3-RP S卧式布局并联机构在工作空间内保持总势能恒定，从而实现该机构的重力补偿，是本文采取的重力补偿策略．基于该策略，在3-RPS卧式布局并联机构的支链 i与机架间安装拉伸弹簧，使其产生与机构重力方向相反的弹簧力，通过弹簧产生的弹性势能补偿机构的重力势能，如图 4所示．考虑到P副的实现方式为套筒-伸缩杆结构，为防止弹簧影响P副的伸缩运动，将弹簧一端固接于套筒上的点 Ei，另一端与并联机构中机架部件的外伸梁固接，其固接点为 Ni，该点在静平台平面的投影为Mi点．

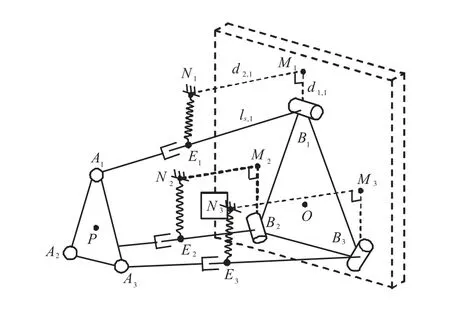
图4 用于重力补偿的弹簧安装Fig.4 Spring installation for gravity compensation

2.2 重力补偿模型

3-RPS卧式布局并联机构中各运动部件均为质量均布结构，其重力可简化为作用于质心的集中力[19]．如图 1所示，机构的运动部件划分为 RPS支链(图 5)与末端执行器(图 6)两部分．其中，RP S支链可进一步划分为：①绕转动副轴线作旋转运动的摆动部件，包括转动副、丝杠、套筒、支撑轴承等零件；②沿移动副移动方向做直线运动的伸缩部件，包括伸缩杆、螺母、球铰副．末端执行器包括动平台和加工装置．

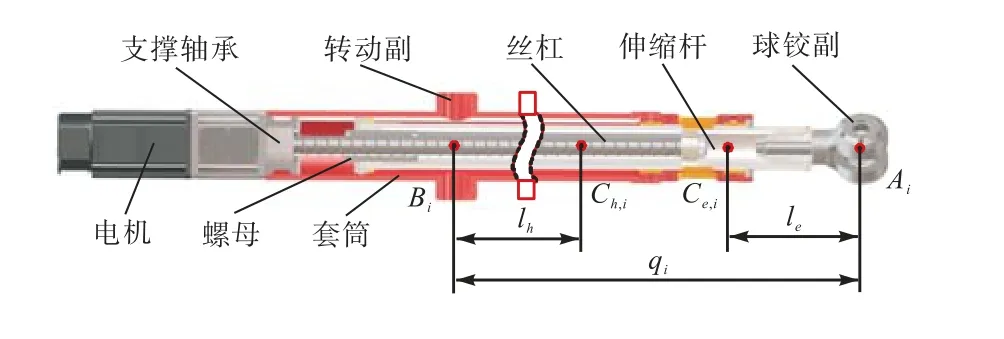
图5 RPS支链结构Fig.5 Structure of RPS limb

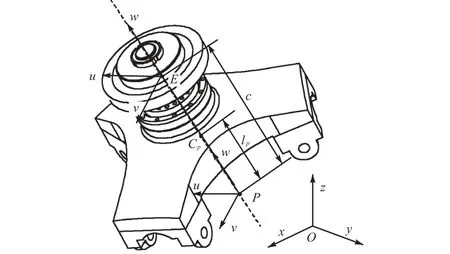
图6 末端执行器结构Fig.6 Structure of end effector

如图 5和图 6所示，机构各运动部件质心在系Oxyz中的位置矢量分别为

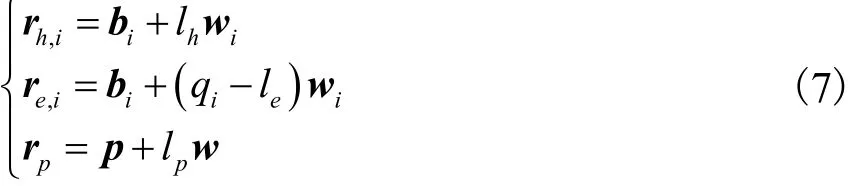
式中：rh,i表示摆动部件质心Ch,i的位置矢量；lh为Ch,i至转动副轴线的距离；re,i表示伸缩部件质心Ce,i的位置矢量；le为Ce,i到球铰副中心的距离；rp表示末端执行器质心 Cp的位置矢量；lp为 Cp到动平台中心点 P的距离；w为在系Oxyz中沿w轴的单位矢量．

由质径积的性质可知，机构总质心在系 Oxyz中的位置矢量c满足

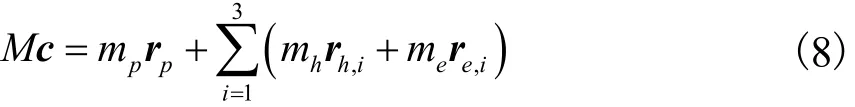
式中：M 为 3-RPS卧式布局并联机构的总质量；mh、me和 mp分别为摆动部件、伸缩部件、末端执行器的质量，且部件质量与总质量满足

则机构的重力势能可表示为

式中：e2为沿重力方向的单位矢量，即上述提及的沿y轴的单位矢量；g为重力加速度．

将式(7)～式(9)代入式(10)，并结合机构的位置逆解，可将 3-RP S卧式布局并联机构的重力势能表示为p的函数．

如图 4所示，因机架外伸梁MiNi垂直于静平台平面且BiMi⊥B2B3，故可构造添加于各支链弹簧的位置方程为

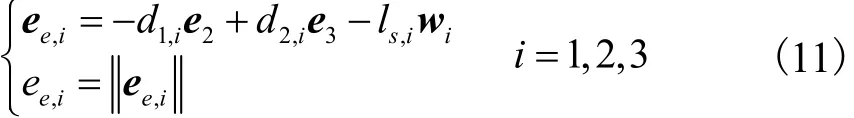
式中：d1,i、d2,i、ls,i分别表示弹簧的位置参数BiMi、MiNi及BiEi；e3为沿 z轴的单位矢量；ee,i为弹簧的长度．

本文重力补偿用弹簧均为线性拉伸弹簧，弹簧的伸长量满足

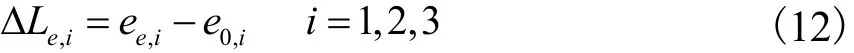
式中e0,i表示弹簧的初始长度．

弹簧在任一状态下由于拉伸弹性形变而具有的弹性势能及弹性力可表示为

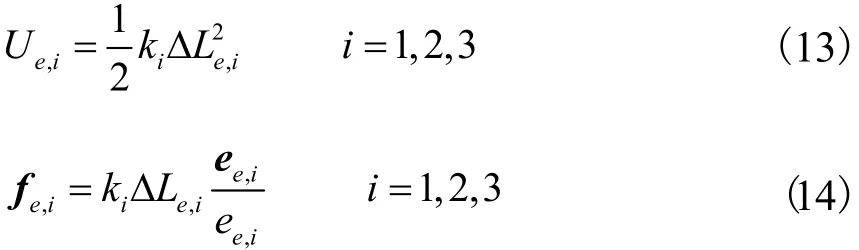
式中ki为弹簧i的刚度系数．

由式(10)～式(13)可知，添加弹簧元件后，3-RP S卧式布局并联机构在工作空间内任一位姿下所具有的总势能可表示为

2.3 参数优化设计

在3-RPS卧式布局并联机构中添加弹簧元件后，需使机构总势能在工作空间中尽可能保持一致，以此实现机构的重力补偿．因此，有必要对弹簧的安装位置及其刚度系数等参数进行优化设计．

2.3.1 目标函数及设计变量

为使机构总势能在工作空间内尽可能保持一致，当机构重力势能达到最大值时弹簧提供的弹性势能应为最小值，据此构建优化设计的目标函数为

式中Ug,max为机构重力势能的最大值．则式(16)所示目标函数的意义为：以重力势能最大值为基准，工作空间内机构总势能相对该基准的最大波动量．

如图 2所示，3-RPS卧式布局并联机构的支链2、3关于y轴呈对称布置，故弹簧2和3的刚度、初始长度及安装位置参数满足

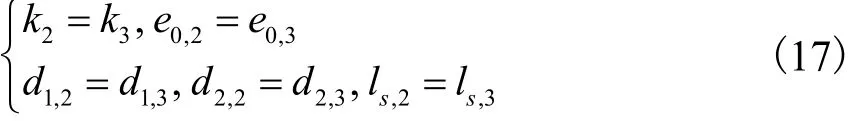
由机构重力补偿模型可知，弹簧的设计参数包括弹簧初始长度e0,i，弹簧刚度系数ki，弹簧安装位置参数 d1,i、d2,i及 ls,i．

2.3.2 约束条件

如图 4所示，d1,i仅影响弹簧初始长度 e0,i，在保证机架外伸梁不与机构发生干涉前提下，其取值可根据机架实际结构预先给定．

前期研究[20]表明，3-RP S卧式布局并联机构的重力主要集中于末端执行器，为使弹簧与机构运动部件的安装点尽量靠近机构总质心，可将 Ei点定为套筒端部，即满足式中lt为套筒端部到转动副中心的距离．

通过对第 2.2节中重力补偿模型分析可知，当机构处于z = d 、θ =θmax、ψ=45°的位姿时，机构重力势能最大(其中，d为机构末端沿 z向的行程为零且静、动平台相互平行时，点O、P之间的距离；θmax为动平台相对于静平台的最大摆角)．

为使机构在上述位姿时弹簧弹性势能最小，令安装于支链 1的弹簧在该位姿时伸长为零．各弹簧的参数满足

式中 ee′,1为机构处于重力势能最大位姿时弹簧 1的长度．

综上所述，3-RP S卧式布局并联机构重力补偿的参数优化问题可归结为

设计参数满足的约束条件 cj(s)见式(18)和式(19)．

3-RPS卧式布局并联机构中各运动部件的重力参数及几何参数详见表 1和表 2，借助 MATLAB软件中的优化算法工具箱 GA(图 7)，可计算求得满足设计要求的弹簧参数，结果如表3所示．

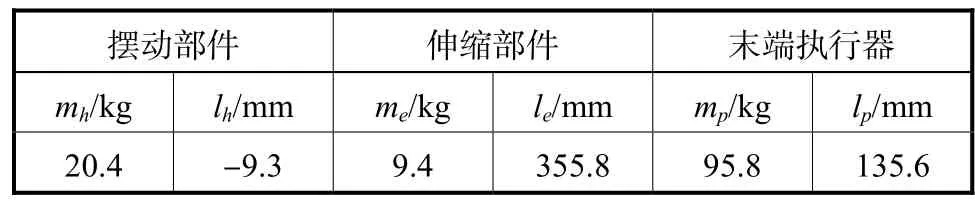
表1 机构重力参数Tab.1 Gravity parameters of manipulator

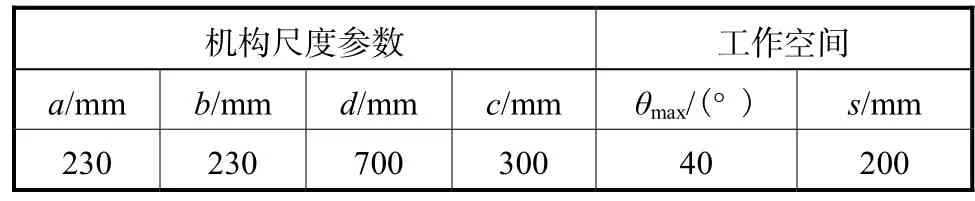
表2 机构尺度参数与工作空间Tab.2 Dimensional parameters and prescribed workspace of manipulator

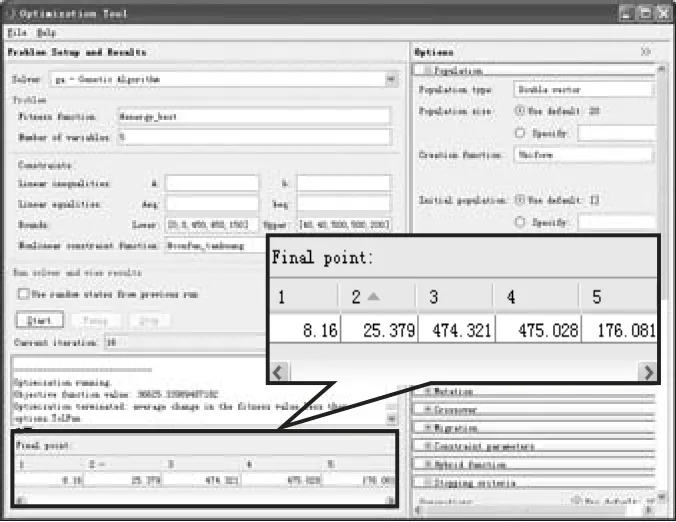
图7 MATLAB算法工具箱优化结果Fig.7 Optimal results with MATLAB algorithm tool

表3 参数优化结果Tab.3 Optimal results of parameters

3 重力补偿效果评估与校核

重力可视为施加于机构的外载荷，机构受到外载荷作用时产生弹性形变，机构末端参考点发生偏移，直接影响机构的加工精度．添加重力补偿装置可减小重力对机构的影响，下文将从机构末端参考点的变形考察重力补偿的效果，验证该重力补偿装置的有效性．首先建立机构的静柔度模型，随后检验重力补偿前后末端参考点的变形情况．

3.1 整机静柔度模型

假设3-RP S卧式布局并联机构各部分的静变形均属弹性小变形范畴，满足线性叠加原理．由于机架柔度远小于机构其他部件的柔度，其弹性变形可忽略不计．因此，分别建立3-RP S卧式布局并联机构及末端执行器的柔度矩阵，利用线性叠加原理即可构造整机柔度模型

式中：C为整机静柔度矩阵；Eτ和EΔ为机构末端E点所受广义外力及相应的变形；1EΔ、2EΔ分别表示由机构及末端执行器柔度引起的机构末端变形．

3.1.1 机构柔度矩阵

动平台中心点P与机构末端参考点E之间的变形满足映射关系

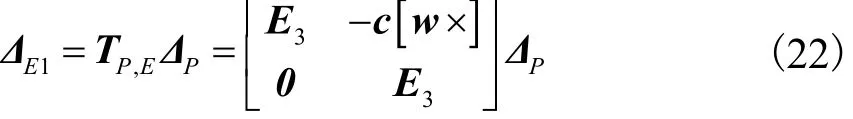
式中：ΔP为动平台中心点P处的弹性变形，且该点处所受内力为τP；E3为单位矩阵．此处及后文中提到的[ε × ]均代表矢量ε的反对称矩阵．

由虚功原理及本构关系可知

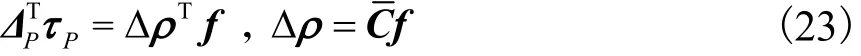
式中 f、Δρ、C分别为各支链末端内力构成的力矢量、变形及柔度矩阵．

RPS支链变形与动平台中心 P点变形之间的映射关系满足

式中J为机构的全阶雅可比矩阵[20]．

由式(22)～(24)及本构关系可得，3-RPS卧式布局并联机构引起的机构末端变形及柔度矩阵为

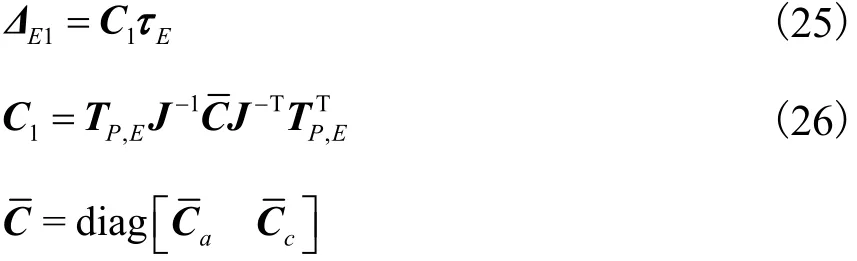
式中Ca、Cc分别为考虑支链轴向变形和弯曲变形的静柔度矩阵，可通过对相应的静刚度矩阵Ka、Kc求逆获得．

如图 5所示，由 RPS支链的具体机械结构及力传递关系知，Ka、Kc可表示为

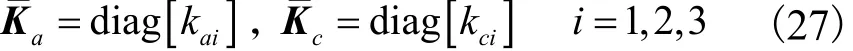
式中对角元素 kai、kci分别表示第 i条支链的轴向拉压刚度系数和沿转动副轴线方向的弯曲刚度系数，可将它们抽象成串联弹簧系统并得

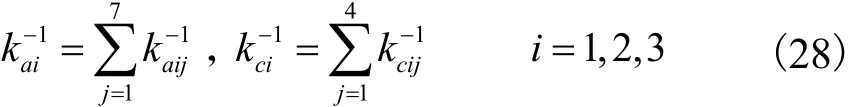
式中：kaij(j＝1～7)分别为 RPS支链各构件的轴向刚度；kcij(j＝1～4)分别为 RP S支链中球铰副、伸缩杆、套筒及转动副部件的弯曲刚度．

3.1.2 末端执行器柔度矩阵

在 E点建立与系 Puvw平行的瞬时参考坐标系Euvw．在系Euvw中，由虚功原理及本构关系知

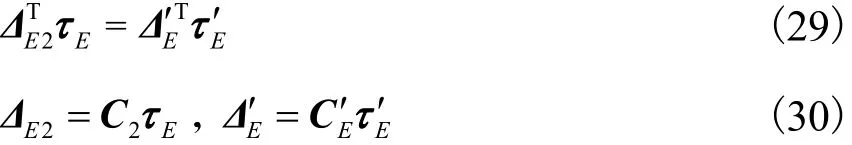
式中：τ′E、ΔE′分别为末端执行器在参考点 E处所受的内力和相应变形；C2为末端执行器柔度映射到机构末端的静柔度矩阵；CE′为末端执行器的静柔度矩阵，其各向柔度通过有限元软件提取．

通过坐标变换，将上述局部坐标系中变量转换到系Oxyz中可得

式中RE为系Euvw相对于系Oxyz的旋转变换矩阵，满足

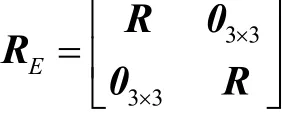
综上所述，将式(25)及式(30)代入式(21)，可得整机静柔度矩阵为

3.2 重力引起的机构末端变形

由构建的柔度模型可知，重力补偿前后与重力相关的机构末端变形gΔ、,geΔ分别为

式中gτ、τ分别为机构的运动部件总重力、重力与弹簧合力映射到机构末端的广义力矢量，且满足

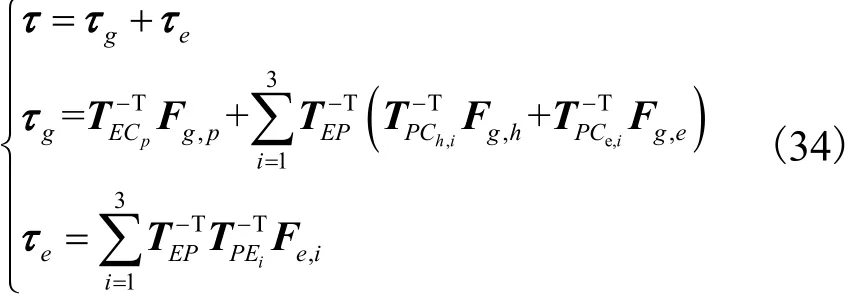
式中：TPCh,i、TPCe,i分别为部件质心点 Ch,i、Ce,i与动平台中心点P之间的伴随变换矩阵；TPEi为各支链弹簧安装点 Ei与 P点之间的伴随变换矩阵；TECp、TEP分别为点Cp、P与机构末端点E之间的伴随变换矩阵；Fg,h、Fg,e、Fg,p分别表示摆动部件、伸缩部件及末端执行器的6维重力矢量；Fe,i为各支链弹簧的6维弹簧力矢量．各矩阵可表示为

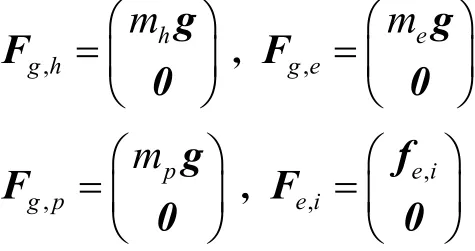
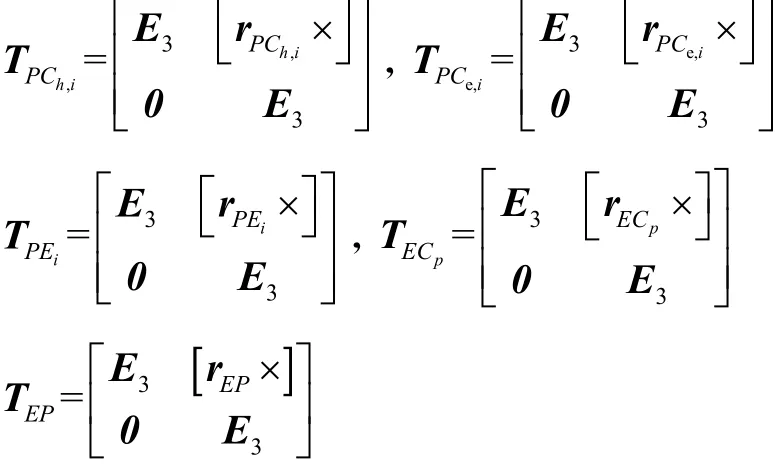
其中

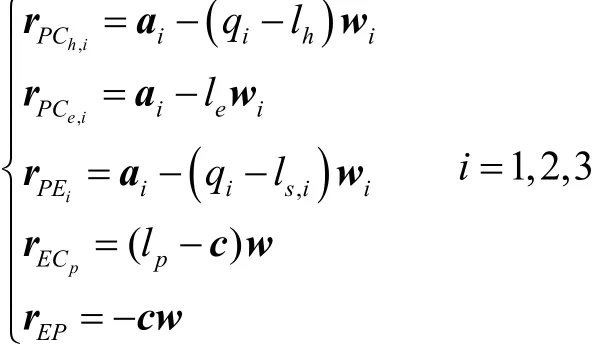
由于重力对 3-RPS卧式布局并联机构末端沿重力方向的线变形影响最为显著，故在此以机构末端参考点在工作空间中沿 y轴方向的线变形校验重力补偿的效果．

给定3-RPS卧式布局并联机构的主要尺度参数及任务工作空间(见表 2)，机构重力参数及重力补偿优化参数如表 1和表 3所示，工作空间如图 8所示.图9所示为重力补偿前、后机构重力造成的末端沿y轴方向的线变形在工作空间内的分布规律，图中纵坐标Δg,,y为仅存在重力作用时的末端变形，Δge,,y为添加重力补偿装置后，重力与弹簧力合力产生的末端变形．由图可知，Δg,,y、Δge,,y关于θy=0°呈面对称分布，Δge,,y关于θx=0°近似呈面对称分布；重力补偿前，Δg,,y随着 z的增加而增大，即不论机构处于何种姿态，随着3-RP S卧式布局并联机构支链的伸长，重力造成的机构末端变形均增大；重力补偿后，重力产生的末端变形 Δge,,y随 z值的变化基本消除，且末端的变形值均控制在以零为中心的微小范围内．

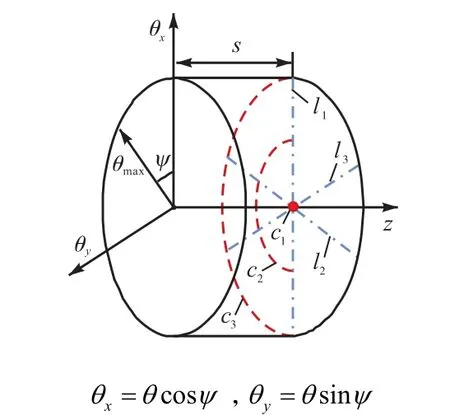
图8 工作空间内的典型位姿分布Fig.8 Typical configurations within workspace

选取工作空间z d s= + 截面内的弧 c1～c3、线l1～l3(图 8)来直观考察 Δg,,y、Δge,,y随转角 ψ、θ 的变化规律，结果如图10和图11所示，图中纵坐标Δy统指机构末端沿 y轴方向的线变形．Δg,,y、Δge,,y关于ψ=180°对称，故仅考察ψ=0°～180°时，Δg,,y、Δge,,y的变化规律．

如图10所示，当z为定值时，Δg,,y随着ψ的增大而减小，即加工装置末端绕z轴从工作空间下端转动到上端时，重力造成的机构末端变形增大，ψ=0°时，Δg,,y达到最大值；重力补偿后，Δge,,y均有不同程度的减小，且随着ψ的增加先增大后减小，ψ趋近于0°或180°时，Δge,,y趋近于零．如图 11所示，当 z、ψ 为定值时，Δg,,y随着θ单调递增，重力补偿后，Δge,,y随着θ的正向或负向增加而增大，即θ=0°重力补偿最好．

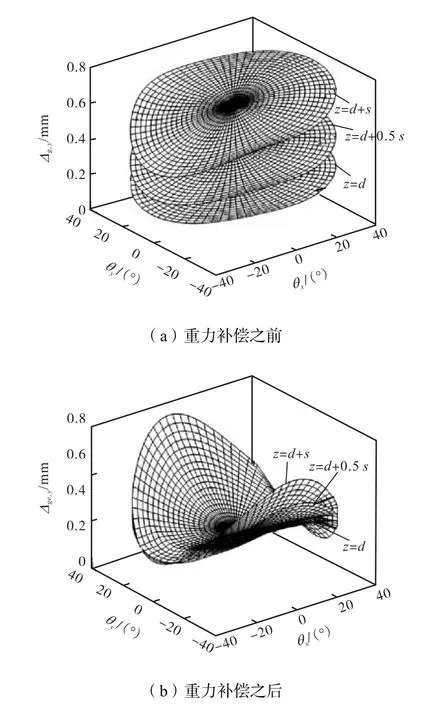
图9 机构末端y向线变形在ψ-θ工作空间内的分布Fig.9 Distribution of y-direction deformation in the ψ-θ workspace

综上分析可知，3-RPS卧式布局并联机构的重力会使其末端产生较大变形，最大值可达到 728,μm，对机构末端定位精度有很大影响．通过添加弹簧元件实现重力补偿后，重力引起的机构末端变形得到很大程度的降低，在某些位姿下甚至可实现完全补偿，补偿效果明显．

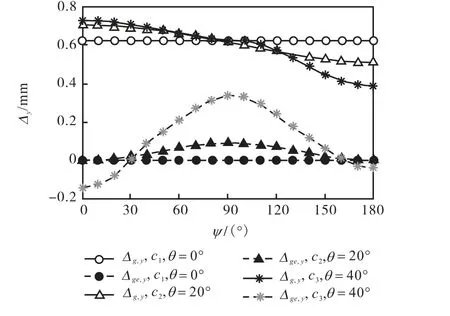
图10 z＝d＋s时Δg,,y和Δge,,y随ψ的变化规律Fig.10 Variation of Δg,,y，Δge,,y with ψ when z＝d＋s

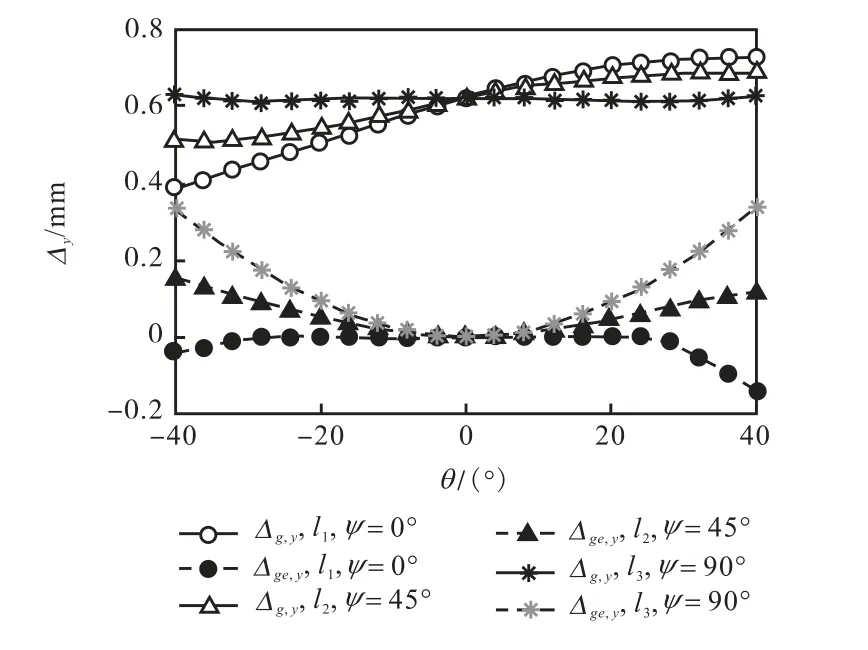
图11 z＝d＋s时Δg,,y和Δge,,y随θ的变化规律Fig.11 Variation of Δg,,y，Δge,,y with θ when z＝d＋s

4 结 论

(1) 选用定刚度螺旋拉簧为重力补偿元件，以机构总势能在工作空间中的波动量最小为目标，施以约束条件，完成了弹簧安装位置及相关参数的优化设计．

(2) 利用线性叠加原理构造了机构的静柔度半解析模型，并通过重力补偿前、后的效果对比，校核了重力补偿策略的有效性．

(3) 添加弹簧元件后，尽管机构的重力补偿效果明显，但依然无法实现机构在整个工作空间内的重力完全补偿，越靠近工作空间边界，补偿效果越差．因此，在后续重力补偿策略研究中，应该重点考虑在摆角θ的极限位置处的重力补偿．

［1］ 宋轶民，张嘉滕，孙 涛. 一种 1T2R 并联动力头的运动学分析与优化设计[J]. 天津大学学报：自然科学与工程技术版，2014，47(10)：863-870.Song Yimin，Zhang Jiateng，Sun Tao. Kinematic analysis and optimal design of a 1T2R parallel manipulator[J]. Journal of Tianjin University：Science and Technology，2014，47(10)：863-870(in Chinese).

［2］ 宋轶民，申 贞，董 罡，等. 一种球坐标型并联机构的弹性动力学分析[J]. 天津大学学报：自然科学与工程技术版，2014，47(5)：401-407.Song Yimin，Shen Zhen，Dong Gang，et al. Elasto-Dynamic analysis of a spherical coordinate parallel mechanism[J]. Journal of Tianjin University：Science and Technology，2014，47(5)：401-407(in Chinese).

［3］ 宋轶民，程 航，孙 涛，等. 并联机构转动副滚动轴承静刚度参数辨识[J]. 天津大学学报：自然科学与工程技术版，2014，47(12)：1101-1108.Song Yimin，Cheng Hang，Sun Tao，et al. Static stiffness identification of rolling bearings in parallel mechanisms with revolute joints[J]. Journal of Tianjin University：Science and Technology，2014，47(12)：1101-1108(in Chinese).

［4］ 宋轶民，翟学东，孙 涛，等. 一种三自由度冗余驱动并联模块的刚度分析[J]. 天津大学学报：自然科学与工程技术版，2015，48(1)：25-32.Song Yimin，Zhai Xuedong，Sun Tao，et al. Stiffness analysis of a 3-DOF redundantly actuated parallel module[J]. Journal of Tianjin University：Science and Technology，2015，48(1)：25-32(in Chinese).

［5］ 孙 涛，宋轶民，李永刚，等. 一类四自由度混联可重构主模块的全域静刚度预估[J]. 天津大学学报，2010，43(11)：1003-1008.Sun Tao，Song Yimin，Li Yonggang，et al. Global stiffness estimation of 4-DoF hybrid and reconfigurable module[J]. Journal of Tianjin University，2010，43(11)：1003-1008(in Chinese).

［6］ Neumann K E. Tricept application[C]//Proceedings of 3rd Chemnitz Parallel Kinematics Seminar. Zwickau，Germany，2002：547-551.

［7］ Hennes N，Staimer D. Application of PKM in aerospace manufacturing high performance machining centers ECOSPEED，ECOSPEED-F and ECOLINER[C]//Proceedings of 4th Chemnitz Parallel Kinematics Seminar. Chemnitz，Germany，2004：557-577.

［8］ 孟祥志，李树军. 并联机床的平衡机构设计及优化[J]. 中国机械工程，2010，21(15)：1794-1797.Meng Xiangzhi，Li Shujun. Design and optimization of balancing mechanism for a parallel machine tool[J].China Mechanical Engineering，2010，21(15)：1794-1797(in Chinese).

［9］ 陈有清. 3-(2SPS)三平移并联机构静平衡研究[D]. 南京：南京理工大学机械工程学院，2011.Chen Youqing. Study of the Static Balance Scheme Based on 3-(2SPS)Parallel Mechanism[D]. Nanjing：School of Mechanical Engineering，Nanjing University of Science & Technology，2011(in Chinese).

［10］ 贺长顺. 机器人平衡系统的设计[J]. 制造技术与机床，1990(1)：16-18.He Changshun. Design of the balance system of robot[J]. Manufacturing Technology & Machine Tool，1990(1)：16-18(in Chinese).

［11］ Gosselin C M，Wang Jiegao. On the design of gravitycompensated six-degree-of-freedom parallel mechanisms[C]//Proceedings of 1998 IEEE International Conference on Robotics & Automation. Leuven，Belgium，1998：2287-2294.

［12］ Wang Jiegao，Gosselin C M. Static balancing of spatial four-degree-of-freedom parallel mechanisms[J]. Mechanism and Machine Theory，2000，35(3)：563-592.

［13］ Russo Andrea，Sinatra Rosario，Xi Fengfeng. Static balancing of parallel robots[J]. Mechanism and Machine Theory，2005，40(2)：191-202.

［14］ 孟祥志，刘春时，李 明，等. 3-PRS型并联机床的配重平衡法[J]. 东北大学学报：自然科学版，2009，30(9)：1322-1325.Meng Xiangzhi，Liu Chunshi，Li Ming，et al. On the counterweight law of 3-PRS parallel machine tool[J].Journal of Northeastern University：Natural Science，2009，30(9)：1322-1325(in Chinese).

［15］ Ebert-Uphoff I，Gosselin C M，Laliberté T. Static balancing of spatial parallel platform mechanisms—Revisited[J]. Transactions of the ASME：Journal of Mechanical Design，2000，122(1)：43-51.

［16］ 何 雷，孙汉旭，贾庆轩，等. 基于静平衡原理的机械臂重力补偿方法研究[J]. 机电产品开发与创新，2013，26(1)：9-11.He Lei，Sun Hanxu，Jia Qingxuan，et al. The manipulator gravity compensation method based on the principle of static equilibrium[J]. Development & Innovation of Machinery & Electrical Products，2013，26(1)：9-11(in Chinese).

［17］ 吴孟丽，王立文. 一种新型并联机器人的静力学优化设计[J]. 中国机械工程，2010，21(19)：2308-2312.Wu Mengli，Wang Liwen. Statics optimum design of a new parallel robot[J]. China Mechanical Engineering，2010，21(19)：2308-2312(in Chinese).

［18］ Dehkordi Maryam Banitalebi，Frisoli Antonio，Sotgiu Edoardo，et al. Modelling and experimental evaluation of a static balancing technique for a new horizontally mounted 3-UPU parallel mechanism[J]. International Journal of Advanced Robotic Systems，2012，9(193)：1-12.

［19］ 李俊峰，张 雄. 理论力学[M]. 北京：清华大学出版社，2010.Li Junfeng，Zhang Xiong. Theoretical Mechanics[M].Beijing：Tsinghua University Press，2010(in Chinese).

［20］ Li Yonggang，Liu Haitao，Zhao Xueman，et al. Design of a 3-DOF PKM module for large structural component machining[J]. Mechanism and Machine Theory，2010，45(6)：941-954.