基于混沌时间序列法的微网短期负荷预测

李东东，覃子珊，林顺富，郑小霞，王天祥

（1.上海电力学院上海市电站自动化技术重点实验室，上海200090；2.金华电业局，金华321015）

基于混沌时间序列法的微网短期负荷预测

李东东1，覃子珊1，林顺富1，郑小霞1，王天祥2

（1.上海电力学院上海市电站自动化技术重点实验室，上海200090；2.金华电业局，金华321015）

针对微网中居民小区用电量较低、负荷波动大的特点，提出了结合混沌理论重构相空间并建立最大Lyapunov指数模型的方法。该方法不直接考虑影响负荷的气候、电价等因素，输入数据参数较少，采用C-C方法求延迟时间与嵌入维，运用改进的最大Lyapunov指数方法进行预测。将此方法用于安徽某一小区的实际负荷数据预测，预测结果表明该算法的预测精度较高，可以为微网的优化运行提供负荷依据，仿真结果验证了算法的有效性和实用性。

短期负荷预测；混沌；Lyapunov指数；微网；分时电价

短期负荷预测是电力系统的一项基本工作，是调度安排开停机计划的基础，其预测精度直接影响电力系统的经济效益[1]。微网可作为配电系统的负荷运行，也可作为电源向配电系统供电。因此，研究微网短期负荷预测，制定合理的发供电计划，对大电网和微网系统的运行均具有重要的意义。

目前，短期负荷预测主要采用时间序列法[2]、灰色预测[3]、神经网络[4]以及各种加权组合方法[5]等。但微电网中电力负荷有时只有几十到几百千瓦，容量较小，突变很大，且受多种因素的影响，如电价、用电习惯、政策等，如选用上述算法，很难建立准确的数学模型进行预测。文献[6]提出了一种基于短期负荷预测的微网储能系统主动控制策略，但是微网短期负荷预测只做了相关介绍，没有给出具体的计算方法；文献[7]从经济性和低碳化两方面考虑智能微网运行的整体效益，将负荷及分布式电源出力按时段划分进行日前优化调度，而负荷的预测数据是直接给出的。混沌理论是非线性动力学的重要发展，负荷时间序列的非线性及不确定性表现出混沌性质，且混沌时间序列法在很多领域都得到了应用。

本文利用真实采集的小区负荷数据，不做任何假设，不直接考虑与负荷相关的随机因素，而是直接对含有受气候和电价等因素影响的负荷历史数据进行分析，根据特征客观性，利用最大Lyapunov指数模型进行预测。结合微网经济运行的特点，提出了时段相对误差作为考核短期负荷预测的指标，通过仿真验证了该方法的可行性。

1 微网短期负荷预测

微网是指由分布式电源、储能装置、能量变换装置、相关负荷及监控、保护装置汇集而成的小型发配电系统，既可以与大电网并网运行，也可以孤立运行。分布式电源的出现，要求电网与用户侧双向互动，以此引导用户优化用电方式，达到提高终端用电效率、优化资源配置的目的，但这也给传统的用电负荷提出了新的挑战。根据《国家电网公司“十二五”电力营销发展规划》的总体目标，要全面建设电力用户的用电信息采集系统[8]。智能电表是实现智能化管理的必须环节。智能电表的一个重要用途就是用采集到的负荷数据对负荷进行分析和预测[9]。对于整个微网，通过采集微网各用户智能电表中的历史数据对其日负荷曲线进行预测。

短期负荷预测是微网经济优化运行的前提，而预测的准确度也直接影响优化的效果。由于微网经济运行时通常要考虑储能单元的工作寿命及运行成本，解决的方法是在充分发挥储能单元作用的同时尽量减少储能系统充放电次数。因此，考虑到夜间与白天的电价差，应控制储能系统在夜间电价低，负荷较轻时充电，在白天电价高，负荷较重时放电。因此，负荷某一时段的总量对控制储能系统具有更直接的意义。本文根据6时段3级分时电价标准[10]将一整天负荷分为6个时间段负荷总量进行分析，时段分为：1时段为23：00—07：00；2时段为07：00—10：00；3时段为10：00—15：00；4时段为15：00—18：00；5时段为18：00—21：00；6时段为21：00—23：00。其中，峰时段为3和5时段，谷时段为1时段，平时段为2、4、6时段。

本文根据上述划分的6时段，提出了一种新的误差衡量指标，即时段相对误差E，表示为

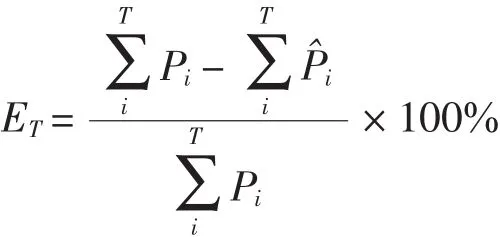
式中：ET为某一时段负荷总量的相对误差；Pi为某一时段内某一时刻的负荷真实值；Pˆi为某一时段内某一时刻的负荷预测值。

2 基于改进的最大Lyapunov指数混沌时间序列方法

2.1 混沌时间序列法基本理论

在实际的短期负荷数据中，往往表现出多变量动态演化行为和多层次结构等，表现出混沌性质。混沌预测正是利用混沌吸引子在不同层次间的自相似性进行混沌系统的短期预测，通过相空间重构来近似恢复原来的多维非线性混沌系统。

按照Takcns定理可以在拓扑等价意义下恢复吸引子的动力学特性。对于时间序列{xi：i=1，2，…，n}，如果能恰当选取嵌入维数m和延迟时间τ，重构其相空间为

式中，N为向量序列的长度，N=n-（m-1）t。

2.2 基于最大Lyapunov指数的改进算法

Lyapunov指数作为对初始轨道的指数发散和估计系统的量化混沌量，是系统的一个很好的预报参数，在电力系统短期预报等领域中有着广阔的应用前景[12]。运用改进的最大Lyapunov指数方法步骤如下。

步骤1对单变量时间序列{x（ti），i=1，2，…，N}进行FFT变换，计算平均周期P。

步骤2用C-C方法同时计算出嵌入维数m和时间延迟τ，本文采用文献[13]中改进的C-C方法对参数进行计算得Smean、delta Smean、Score，根据求得的结果做图。

步骤3根据步骤2求出的嵌入维数m和时间延迟τ重构相空间{Xi，i=1，2，…，M}。

步骤4在步骤3重构的相空间中找到任意每个点Xj的最近邻点Xjˆ，并限制短暂分离，即

步骤5对相空间中任意每个点Xj，计算出该邻点对应的i个离散时间步后的距离dj（i），即

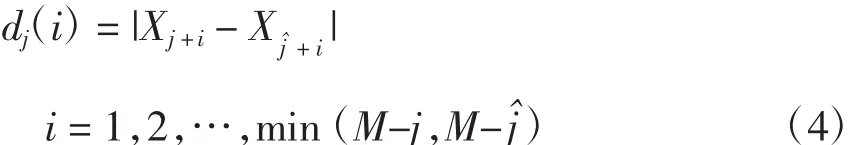
步骤6对每个i，计算出所有j的ln dj（i）平均值y（i），即

式中，q为非零dj（i）的数目，并用最小二乘法做出回归直线，该直线的斜率就是最大的Lyapunov指数λ1。

2.3 基于最大Lyapunov指数的预报模型

不防设XM为预报的中心点，相空间中XM的最近的邻点为Xk，其距离为dM（0），最大Lyapunov指数λ1，则

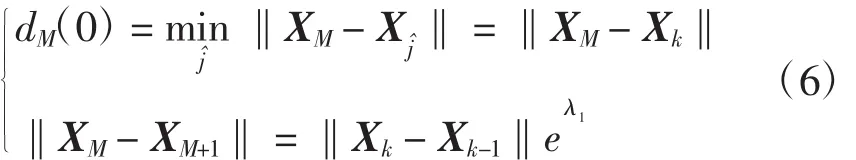
其中：XM+1点只有最后一个分量x（Xn+1）未知，故x（Xn+1）是可预报的。式（6）就是基于最大Lyapunov指数的预报模式，其解有2个，判断预测值的正、负取值，可根据前2个相似日的平均值决定，也可参考文献[14]中提出的改进方法进行选取。

3 算例仿真及误差分析

现以安徽省池州市某小区2012-09-10—2012-09-29共20 d（取15 min一个点，每日96点，共1 920点）的真实历史负荷数据为研究对象，其时间序列如图1所示。

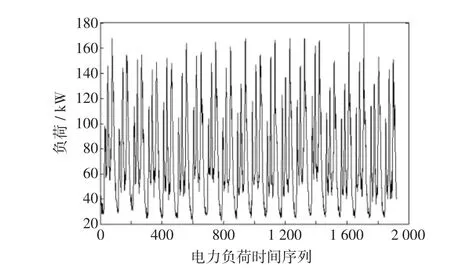
图1 安徽某小区2012-09-10—2012-09-29负荷时间序列Fig.1Load time series of a certain community in Anhui province from Sep.10th to 29th，in 2012

3.1 参数计算

首先对这1 920个数据进行谱分析，用FFT计算得平均周期P＝48。采用改进的C-C方法作相空间重构计算，其结果如图2所示。

从图2中可以看到，ΔS（t）第1次取极小值时，t=5，因此延迟时间取τ＝5；而Scor（t）取最小值时，t=95，所以最佳嵌入窗宽τw＝95，根据嵌入窗公式τw=（m-1）τ，可得m=20。

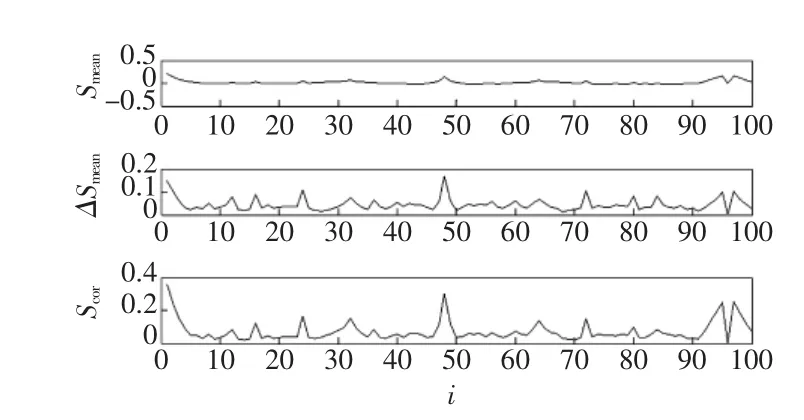
图2 重构参数的C-C法Fig.2C-C method of reconstruction parameters

根据求得的延迟时间和重构维数对时间序列进行相空间重构，求该负荷时间序列的最大Lyapunov指数，计算结果如图3所示。

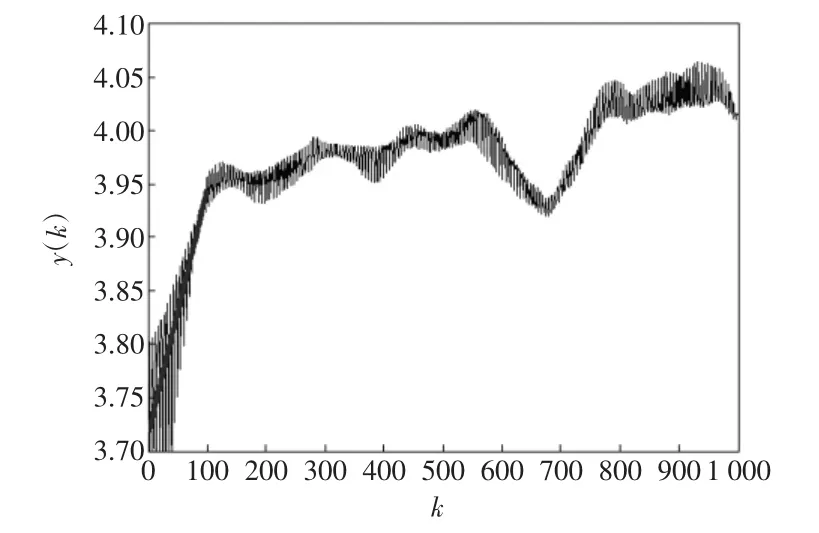
图3负荷时间序列的最大Lyapunov指数计算曲线Fig.3Maximal Lyapunov exponent curve of load time series

图3 中，k为离散时间演化步数，y（k）为所有最近邻点对经k步演化后的距离对数平均值。从图3中可以看出，在k=100以前的一段曲线近似为直线，该直线的斜率即为负荷时间序列的最大Lyapunov指数，由线性回归的最小二乘法可求得该直线的斜率为0.002 3，即有λ1＝0.002 3为正，证明了负荷序列是混沌时间序列，具有混沌特性。

3.2 预测结果

根据最大Lyapunov指数预测模型及前面计算出的参数，对2012-09-30的96点负荷进行预测，结果见图4，预测结果如表1所示。

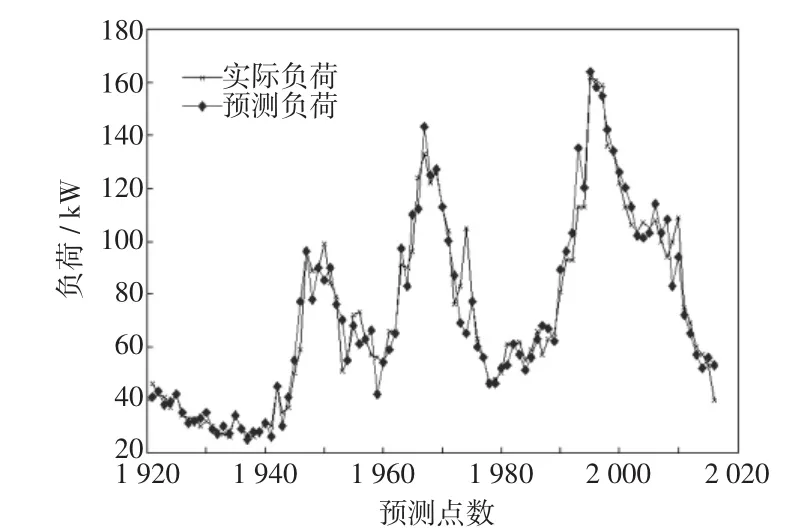
图4 安微某小区2012-09-30实际和预测电力负荷值Fig.4Actual and forcasting load data of a certain community in Anhui province on Sep.30th，2012

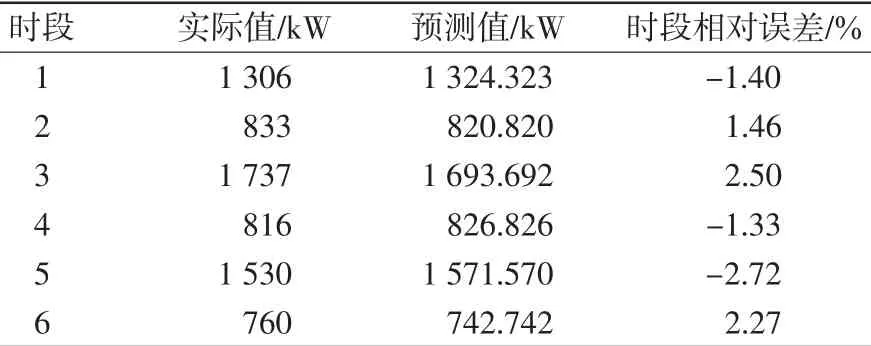
表12012 -09-30的负荷预测结果Tab.1Forecasting results in Sep.30，2012

从表1结果来看，预测的时段相对误差控制在3%以内，最大误差为2.72%，最小误差为1.33%。基于最大Lyapunov指数预测模型由时间序列本身所计算出来的客观规律进行预测，从而避免了人为主观因素的影响。

3.3 误差分析

用相同的方法及步骤，对2012-10-01—2012-10-06的用电量进行了日负荷曲线预测，并对672组数据进行误差统计分析，单点的相对误差分布见图5，预测结果误差见表2，时段相对误差见表3，其中：MAPE为平均相对误差；RMSE为均方根误差

对于不分时段单点的误差情况，图5给出了相对误差概率分布，将落在某一范围内的误差频数用直方图表示，近似接近正态分布，误差控制在10%以内的概率达到72.1%，误差超过20%的仅占8.5%，极端的较大误差只是小概率事件。从表2可以看出，按单点情况统计的平均相对误差为10%左右，均方根误差大约为3 kW。表3中，分时段后各时段的误差情况其全部误差控制在5%以内，最小误差为0.9%，最大误差为4.79%，其中误差在3%以内的占78.6%。本文将混沌时间序列法运用到小区级别的负荷上，预测结果整体的误差指标较好，可为下一步的微网优化运行提供负荷依据。

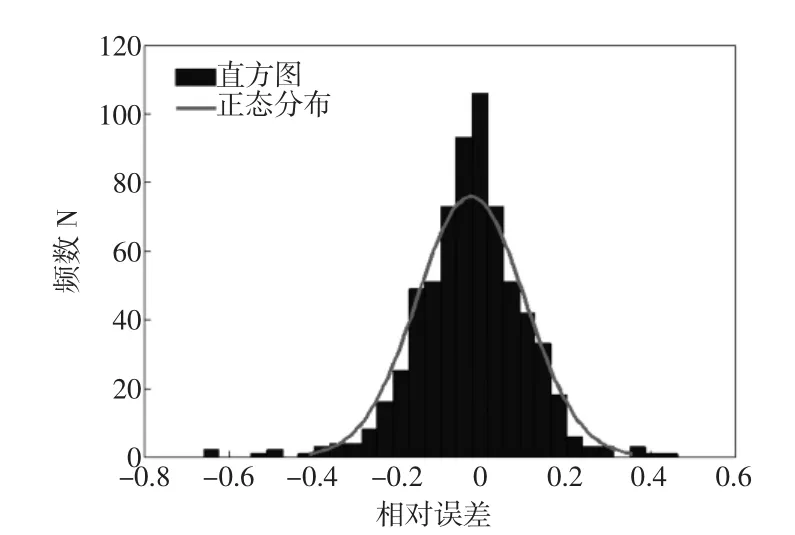
图5 误差分布概率Fig.5Probability plots of error distribution

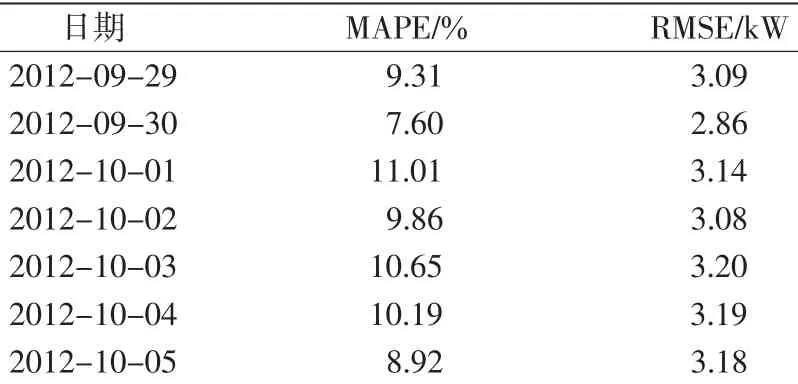
表22012 -09-30—2012-10-06的负荷预测结果误差Tab.2Load forecasting errors from Sep.30 to Oct.6，2012

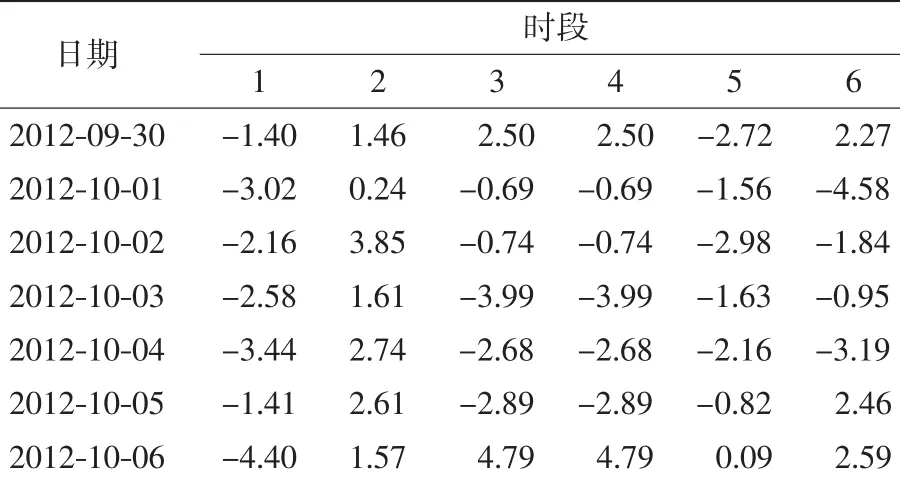
表32012 -09-30—2012-10-06的时段相对误差Tab.3Realelative error in the period of Sep.30 to Oct.6，2012%

4 结语

结合混沌理论，运用改进的最大Lyapunov指数方法，建立了基于混沌理论的微电网负荷预测模型。该方法不需收集温度、电价等信息，而是直接通过相空间重构，运用多维系统里的一维负荷数据进行负荷预测。根据微网的特点，提出了时段相对误差指标，对微网优化运行中储能单元的控制具有更直接的意义。并用此模型，对安徽某小区级别的负荷进行预测，单点的相对误差分布具有近似正态分布特性，时段相对误差控制在5%以内，取得了较为满意的效果。算法不依赖于特定的应用背景，对微网等用电量不大的系统具有一定参考价值。

[1]刘晨辉.电力系统负荷预测理论与方法[M].哈尔滨：哈尔滨工业大学出版社，1987.

[2]陈敏，李泽军，黎昂（Chen Min，Li Zejun，Li Ang）.基于混沌理论的城市用电量预测研究（Forecast research of urban electricity consumption based on chaos theory）[J].电力系统保护与控制（Power System Protection and Control），2009，37（16）：41-45.

[3]王允平，黄殿勋，熊浩清，等（Wang Yunping，Huang Dianxun，Xiong Haoqing，et al）.智能电网环境下采用关联分析和多变量灰色模型的用电量预测（Using relational analysis and multi-variable grey model for electricity demand forecasting in smart grid environment）[J].电力系统保护与控制（Power System Protection and Control），2012，40（1）：96-100.

[4]张平，潘学萍，薛文超（Zhang Ping，Pan Xueping，Xue Wenchao）.基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测（Short-term load forecasting based on wavelet decomposition，fuzzy gray correlation clustering and BP neural network）[J].电力自动化设备（Electric Power Automation Equipment），2012，32（11）：121-125，141.

[5]蒋建东，程志豪，朱明嘉（Jiang Jiandong，Cheng Zhihao，Zhu Mingjia）.考虑积温效应的短期负荷组合预测方法（Combined short-term load forecast with accumulated temperature effect）[J].电力自动化设备（Electric Power Automation Equipment），2011，31（10）：28-31.

[6]陈益哲，张步涵，王江虹，等（Chen Yizhe，Zhang Buhan，Wang Jianghong，et al）.基于短期负荷预测的微网储能系统主动控制策略（Active control strategy for microgrid energy storage system based on short-term load forecasting）[J].电网技术（Power System Techmology），2011，35（8）：35-40.

[7]曹培，王媚，郭创新，等（Chao Pei，Wang Mei，Guo Chuangxin，et al）.智能微网运行的低碳综合效益分析（Analysis on low-carbon integrative benefits of smart microgrid operation）[J].电网技术（Power System Technology），2012，36（6）：15-20.

[8]章欣.智能用电与现代量测技术[M].北京：中国电力出版社，2012.

[9]王思彤，周晖，袁瑞铭，等（Wang Sitong，Zhou Hui，Yuan Ruiming，et al）.智能电表的概念及应用（Concept and application of smart meter）[J].电网技术（Power System Technology），2010，34（4）：17-23.

[10]殷树刚，张宇，拜克明（Yin Shugang，Zhang Yu，Bai Keming）.基于实时电价的智能用电系统（A smart power utilization system based on real-time electricity prices）[J].电网技术（Power System Technology），2009，33（19）：11-16.

[11]武峰雨，乐秀璠，南东亮（Wu Fengyu，Le Xiufan，Nan Dongliang）.相空间重构的极端学习机短期风速预测模型（A short-term wind speed prediction model using phasespace reconstructed extreme learning machine）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（1）：136-141.

[12]吕金虎，陆君安，陈士华.混沌时间序列分析及其应用[M].武汉：武汉大学出版社，2005.

[13]陆振波，蔡志明，姜可宇，等（Lu Zhenbo，Cai Zhiming，Jiang Keyu，et al）.基于改进的C-C方法的相空间重构参数选择（Determinationofembeddingparametersforphase space reconstruction based on improved C-C method）[J].系统仿真学报（Journal of System Simulation），2007，19（11）：2527-2529，2538.

[14]Chan P P K，Wei-Chun Chen，Ng W W Y，et al.Multiple classifier system for short term load forecast of microgrid [C]//International Conference on Machine Learning and Cybernetics.Guilin，China：2011.

[15]李广，谈顺涛（Li Guang，Tan Shuntao）.混沌神经网络在小电网电力负荷中的应用（Application of chaos-ANN model in load forecasting for small regions）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（2）：59-62.

[16]王越，卫志农，吴佳佳（Wang Yue，Wei Zhinong，Wu Jiajia）.人工神经网络预测技术在微网运行中的应用（Application of ANN prediction technology in microgrid operation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：83-89.

Short-term Load Forecasting for Microgrid Based on Method of Chaotic Time Series

LI Dongdong1，QIN Zishan1，LIN Shunfu1，ZHENG Xiaoxia1，WANG Tianxiang2
（1.Shanghai Key Laboratory of Power Station Automation Technology，Shanghai University of Electric Power，Shanghai 200090，China；2.Jinhua Electric Power Bureau，Jinhua 321015，China）

On the basis of the low power consumption and severe fluctuation load of residential area in microgrid，a model of maximum Lyapunov exponent via the phase space reconstruction is constructed combined with chaos theory. This method does not directly consider the impact of factors such as climate，electricity price，thus it requires less input and parameters.It utilizes C-C method to solve the delay time and the embedding dimension，and uses the improved maximum Lyapunov exponent method to forecast.The model is applied to forecast actual load data of a certain community in Anhui province.According to the time of use（TOU），a relative error indicator for time period based on the control of microgrid energy storage charge and discharge system is proposed.Simulation results demonstrate the efficiency and practicality of the algorithm.

short-term load forecasting；chaos；Lyapunov exponent；microgrid；time of use（TOU）

TM715

A

1003-8930（2015）05-0014-05

10.3969/j.issn.1003-8930.2015.05.03

李东东（1976—），男，博士，教授，硕士生导师，研究方向为风力发电与电力系统稳定控制、智能用电。Email：powerldd@163.com

覃子珊（1987—），女，硕士研究生，研究方向为负荷预测、智

能用电及微电网。Email：qinzishan126@126.com

林顺富（1983—），男，博士，教授，硕士生导师，研究方向为电能质量分析、智能用电及节能等。Email：shunfu.lin@163.com

2013-04-22；

2013-12-13

国家自然科学基金项目（50807035，51177098）；上海市重点科技攻关项目（10110502100）；上海市教委创新项目（11ZZ169）；上海市教委重点学科建设项目（J51303）