考虑元件重要度和故障概率影响因素的连锁故障预测

郑国，李华强，邸弢，赵阳，黄燕

（1.四川大学电气信息学院，成都610065；2.国网四川省电力公司检修公司，成都610041）

考虑元件重要度和故障概率影响因素的连锁故障预测

郑国1，李华强1，邸弢2，赵阳1，黄燕1

（1.四川大学电气信息学院，成都610065；2.国网四川省电力公司检修公司，成都610041）

为了更好体现系统实时状态和元件重要程度，提出了一种连锁故障预测新方法。首先建立了考虑功率传输累计效应的线路故障概率模型，并将天气和修复过程对故障概率的影响引入该模型；其次，将支路势能函数引入熵理论，确定了计及能量冲击影响的支路重要程度；最后，构建了反映电网状态变化和元件重要度的连锁故障综合预测指标，并通过在IEEE30系统上进行仿真。仿真结果验证了所提模型及方法的有效性。

连锁故障预测；运行可靠性；支路势能函数；熵

随着电力系统的不断发展，其运行模式和网架结构日益复杂，增加了系统发生故障甚至连锁故障的可能性。近年来，国内外电网发生了多次连锁性大停电事故[1-2]，其主要是由于线路故障开断等扰动导致系统中功率转移，进而引起其他元件相继开断，最终导致系统发生连锁性大停电，并且在其他外部因素影响下，元件故障概率增加。因此对连锁故障序列进行预测，对保证大型电力系统的可靠、稳定运行具有重要的现实意义。

传统连锁故障预测主要是基于复杂系统理论和复杂网络理论。文献[3-5]研究了基于复杂系统OPA模型、CASCADE模型等的理论连锁故障，但同时考虑外界环境因素和内部时变运行状态对故障概率的影响还需进一步研究；基于复杂网络[6-7]的研究大多只考虑电网物理拓扑结构的影响，而实际运行中，系统的可靠性还与时变的运行状态紧密联系；文献[8-9]用最短路径支路的“介数”衡量元件重要程度，并预测连锁故障发展过程，但系统潮流不仅在最短路径中流动，也在其他路径中流动；文献[10]提出的电气介数虽然在这方面有所改进，但仍忽略了系统状态变化后功率转移对剩余元件产生的冲击影响。

本文结合运行可靠性理论与熵理论，提出了一种新的连锁故障预测方法。首先，建立了计及线路从正常运行状态到功率极限过程的累积效应的线路运行可靠性模型，使其相比于现有模型更加符合实际[11-13]，然后结合实际运行中的天气因素和修复过程，利用马尔可夫过程计算连锁故障下线路的故障概率，其次，将支路势能函数引入熵理论，建立了考虑系统有功、无功功率变化的支路重要度模型。最后，综合线路故障概率和重要程度，构建了相应的预测指标，并通过IEEE 30节点系统进行仿真。

1 连锁故障下线路故障概率模型

1.1 基于线路潮流的线路故障概率模型

线路潮流在正常范围以下，其故障概率很低、随着传输潮流不断增加，线路发热量逐渐增加，温度持续上升，可能超过线路热稳定极限，导致故障概率大幅提高，该过程模型如图1所示。

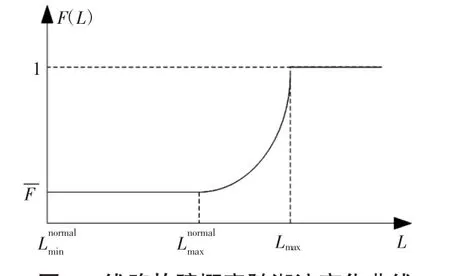
图1 线路故障概率随潮流变化曲线Fig.1Curve of line failure probability varying with transfer capacity

（1）线路潮流在正常范围以下，其故障概率F（L）受潮流影响较小，通常取为故障概率统计值F，即

（2）当线路传输潮流在正常值上限与极限值Lmax之间时，保护装置动作概率随传输潮流增加而增大。本文采用指数形式修正了该过程线路故障概率，即

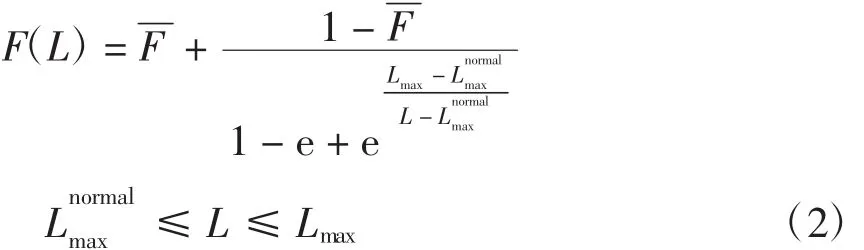
（3）线路传输潮流大于等于极限值，其故障概率常取为1，即

1.2 基于外界环境的线路故障概率模型

利用上述模型，潮流影响下线路故障率F可通过其故障概率求得，即

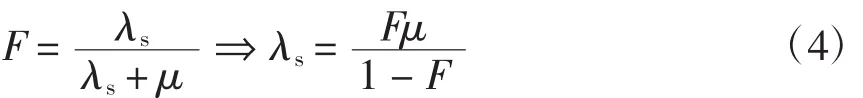
式中：λs为潮流影响下的线路故障率；μ为线路修复率，由于运行条件不影响修复率，因此取为统计平均值。

实际运行中，线路故障率还与其所处天气情况如冰雪、雷雨等相关。虽然这些条件持续时间较短，但这期间线路故障率可能比正常天气条件下大得多。

基于历史统计数据，当线路处于恶劣天气时，不同气象因素影响下线路偶然故障率λc可表示为

式中：λ为线路故障率统计平均值；P为线路处于恶劣天气的概率；F′为线路在恶劣天气下发生故障占总故障次数比例。

所得结果与基于支路潮流运行条件下的支路故障率进行比较，取两者较大值为最终支路故障率，即

式中，λ为综合考虑潮流和天气因素影响下的线路故障率。

1.3 基于马尔可夫过程的线路故障概率

（t1，t1，…，tn）中的时刻按次序t1〈t2〈…〈tn排列，在X（t）=xi（i=1，2，…，n-1）条件下X（tn）= xn的分布函数恰好等于在X（tn-1）=xn-1条件下X（tn）=xn的分布函数，即

这种随机过程称为马尔可夫过程[14-15]。在马尔可夫过程中，时间tn时随机变量概率只与tn-1时随机变量取值有关，与tn-1时刻以前随机变量取值无关。

假设系统中每个元件有2种状态：0为工作状态；1为故障状态。则马尔可夫状态转移如图2所示。

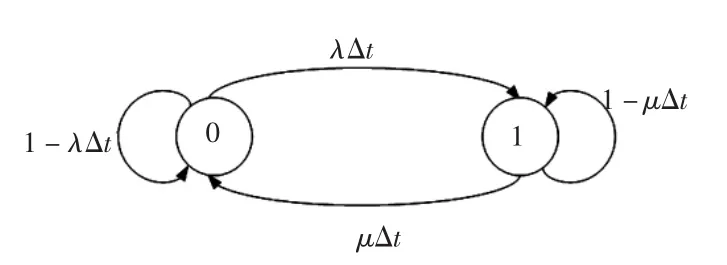
图2 两状态马尔可夫过程Fig.2Two-state Markov process

如果元件连续工作时间TU和故障时间TD服从指数分布，则线路故障率λ、修复率μ为常数，利用齐次马尔可夫过程可得

式中，P（t）=[p（t），q（t）]，p（t）和q（t）为元件工作和故障状态概率。则转移密度矩阵A为

状态概率初始值P（0）为

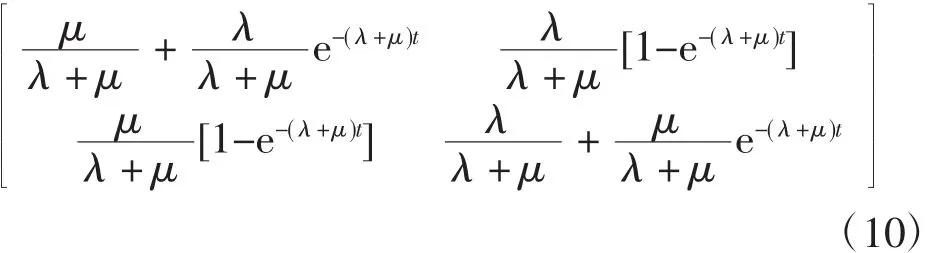
若当前时刻元件处于工作状态，则P（0）=[1，0]，代入式（10）可得

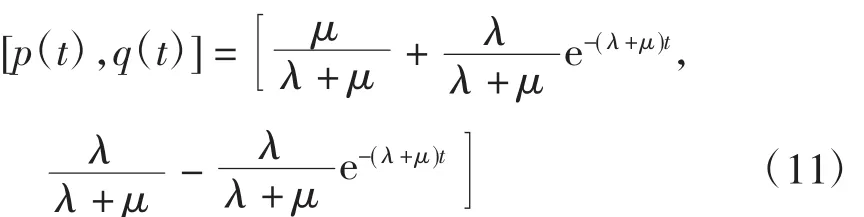
曲线如图3所示。

图3 初始为工作状态p（t）及q（t）变化曲线Fig.3Curves of p（t）and q（t）in working initial state

若当前时刻元件处于故障状态，则P（0）= [0，1]，代入式（10）可得

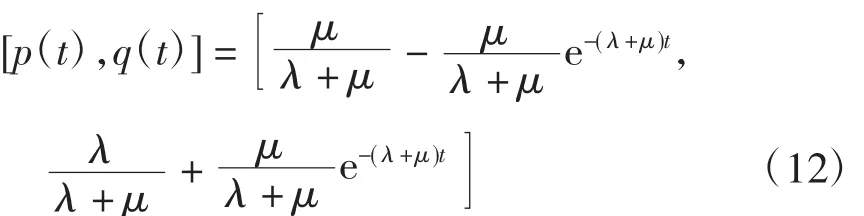
曲线如图4所示。

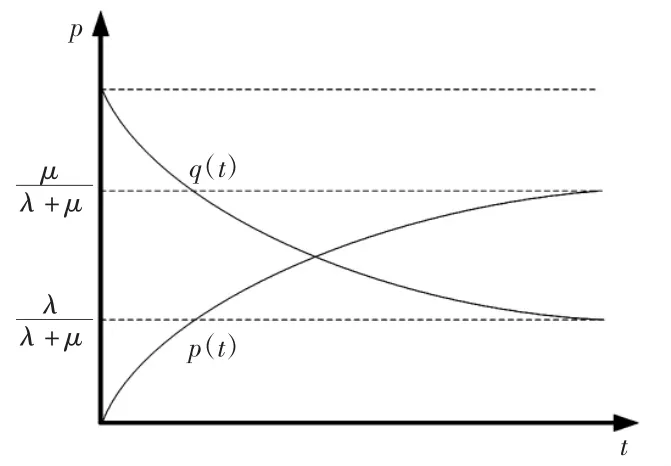
图4 初始为故障状态p（t）及q（t）变化曲线Fig.4Curves of p（t）and q（t）in fault initial state

2 基于熵和支路势能函数的元件重要度模型

2.1 熵理论简介

熵主要是对系统混乱程度的度量，广泛应用于系统稳定程度和不确定性的描述中[16]。当系统状态Xi出现的概率为Pi时，系统熵H定义为式中：C为常数；M为状态数。

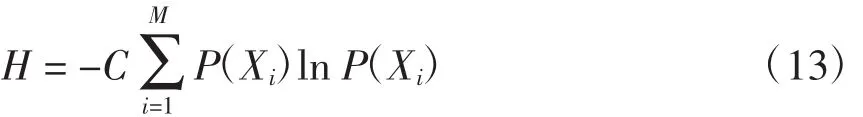
2.2 支路重要度模型

根据文献[17-18]提出的支路势能函数模型，假设当系统发生故障后，若系统过渡到新的稳定状态，则r级故障发生时支路ij的势能变化量为

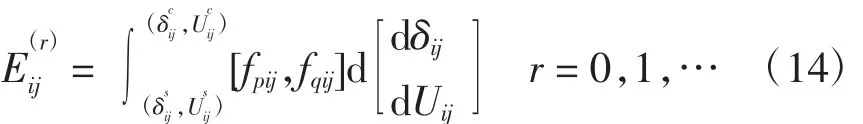
式中：fpij、fqij分别为故障前后支路ij传输有功、无功功率变化量为故障前节点i、j间电压差和相位差为故障后节点i、j间电压差和相位差。

式中，m为系统支路总数。

该支路相应的能量变化熵H(r)为

因此，r级故障断开支路重要度V(r)为

H(r)反映了r级故障支路断开后系统能量重新分布和网络结构改变对系统造成的影响程度。能量变化熵H(r)小，说明少数几条支路承担了断开支路上的转移能量，对应的断开支路的重要程度V(r)越高，能量转移对系统造成的冲击越大，越容易导致剩余支路越限，从而引发连锁故障。

3 基于概率和元件重要度的连锁故障预测

3.1 连锁故障预测指标

假设系统在当前运行状态下，某支路发生故障概率较大，即其在系统中受扰动的可能性较大。但该支路退出运行后，其能量转移量较均匀地分布在系统剩余支路上，没有发生支路越限，则该故障对系统的影响较小。而某些支路虽然故障可能性较小，但一旦退出运行会对系统造成严重影响，甚至引发连锁故障。因此，本文综合了运行可靠性和熵理论等，提出在计及系统当前运行状态下支路故障概率和支路故障后对系统造成影响程度的综合指标S（p，V）。

系统发生r级故障后综合指标S(r)为

式中，p(r)为连锁故障路径经历的第r级故障支路所对应的故障概率。

元件的综合指标越高，表明该元件在系统中越可能对系统带来严重影响。计及前级故障累积效应，系统发生第r级故障后，第r+1级故障线路的预测指标可预测得到，即

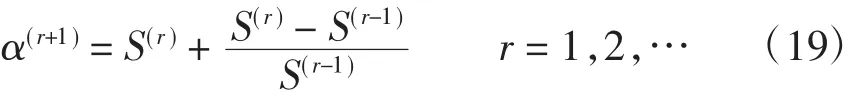
式中：第1项表示在r级故障后的综合指标；第2项表示r级故障后在r-1级故障基础上的综合指标变化率；a(r+1)为发生r级故障后，综合反映系统当前运行状态、历史运行状态和在支路重要度的预测指标，可用于预测出系统较严重的故障模式。

4 连锁故障预测流程

综合上述因素，本文将反映电网状态变化的线路故障概率模型和反映元件重要度模型相结合，提出了连锁故障序列预测的新指标，具体流程如图5所示。

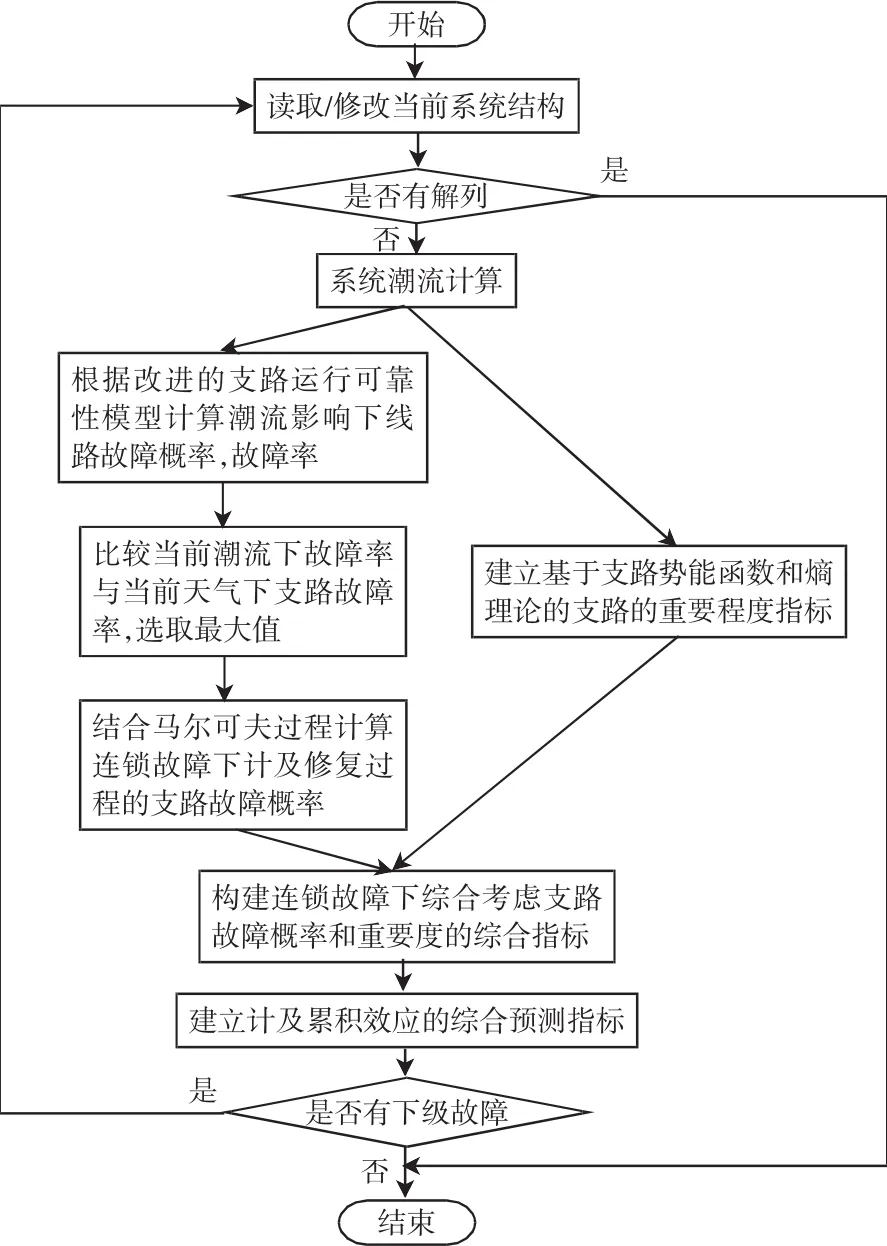
图5 连锁故障预测流程Fig.5Flow chart of cascading failures forecasting

5 算例分析

本文采用IEEE 30节点系统仿真分析，该系统包括41条支路，系统接线如图6所示。仿真故障概率中，t取每级故障后0.05 s。

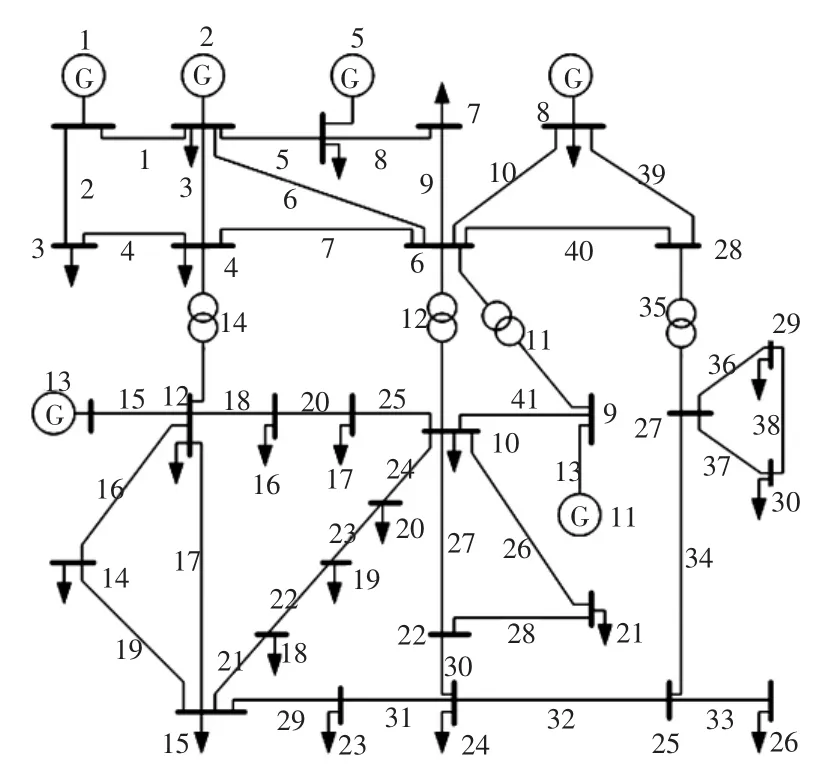
图6 IEEE 30节点系统接线Fig.6ElectricalconnectiondiagramofIEEE30-bussystem

通过运用上述方法，计算初始故障前各支路的综合指标，并选取其指标较高的5条支路，由大到小排序，如表1所示。

表1 初始故障前各支路的综合指标Tab.1Comprehensive index of each branch before the initial failure ×10-3

由表1可以看出，初始故障支路排序中，L1、L2、L5、L8支路为发电机出口线路，若其传输能量接近极限时将极易导致保护动作，线路跳闸可能性较高；支路L11为联络变压器支路，是区域功率交换的关键支路，断开后会使其承担的支路能量重新分布，导致剩余联络变压器支路承担更多的能量传输，从而可能引发下级故障，这应引起运行人员的重视，避免下一级故障的发生。综上，本文方法对引发电网连锁性事故的初始故障起到了较好的辨识作用。

连锁故障部分预测线路及其指标如表2所示。由表2数据可以得出，L1或L2故障后，均极易导致G1平衡机节点与电网脱离，造成系统解列。当L8支路故障跳闸后，会导致从G5发出的功率转移至L6，引起L6支路严重过载，致使其故障率增加。L8与L6支路故障后，导致其最近的变压器支路L14成为3级故障最可能发生的支路。类似的还有L11、L5号支路，这些支路均处于网络能量传输的关键位置，如若故障将导致其附近支路过载，极易引发电网连锁性故障，应该引起运行人员的重点关注。

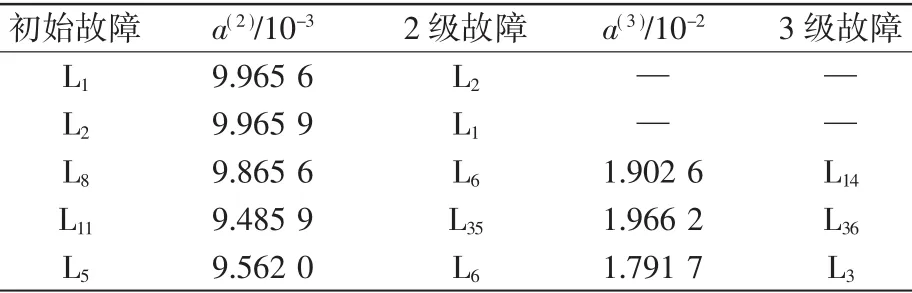
表2 连锁故障部分预测线路及其指标Tab.2Part of lines and cascading failures forecasting indexes

与连锁故障序列对应的综合预测指标随着故障级数增加呈现变大趋势。这是由于每一级故障发生后，系统整体的故障程度加深，无论从故障发生的概率还是故障后的严重程度都有所增加，符合系统实际运行情况。同时，在预测结果中，L6出现次数较其他线路多，属于比较关键的线路，应重点关注。

综上，本文所提出的预测方法对预测连锁故障发生路径有很好的实用效果，可以给运行人员提供直观的决策支持。

6 结语

本文提出了一种综合元件重要度和系统运行状态的连锁故障预测方法。首先建立了考虑线路传输功率在不断增加时，其故障程度加速恶化的过程，并结合实际运行中天气、修复过程等不确定性因素的支路故障概率模型；其次，采用支路势能函数和熵理论，构建了相应的支路重要程度模型，搜素出系统中较严重的故障模式，切合实际，对下级故障辨识度高，为预防电网大停电事故提供了一定参考。

[1]石立宝，史中英，姚良忠，等（Shi Libao，Shi Zhongying，Yao Liangzhong，et al）.现代电力系统连锁性大停电事故机理研究综述（A review of mechanism of large cascading failure blackouts of modern power system）[J].电网技术（Power System Technology），2010，34（3）：48-54.

[2]Andersson G，Donalek P，Farmer R，et al.Causes of the 2003 major grid blackouts in North America and Europe，and recommended means to improve system dynamic performance[J].IEEE Trans on Power Systems，2005，20（4）：1922-1928.

[3]Dobson I，Carreras B，Lynch V，et al.An initial model for complex dynamics in electric power system blackouts[C]// Hawaii International Conference on System Sciences. Maui，USA，2001：710-718.

[4]曹一家，王光增，韩祯祥，等（Cao Yijia，Wang Guangzeng，Han Zhenxiang，et al）.考虑电网拓扑演化的连锁故障模型（A cascading failures model in power grid considering topology evolvement）[J].电力系统自动化（Automation of Electric Power Systems），2009，33（9）：5-10.

[5]Dobson I，Chen J，Throp J S，et al.Examining criticality of blackouts in power system models with cascading events [C]//Hawaii International Conference on System Sciences，Big Island，USA，2002：119-128.

[6]范文礼，刘志刚（Fan Wenli，Liu Zhigang）.基于复杂网络的电网连锁故障模型研究综述（An overview on modeling of cascading failures in power grids based on complex system）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（16）：124-131.

[7]潘一飞，李华强，贺含峰，等（Pan Yifei，Li Huaqiang，He Hanfeng，et al）.小世界网络下电网连锁故障预测（Cascading failures prediction of transmission network in small world network）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（2）：148-153.

[8]孟仲伟，鲁宗相，宋靖雁（Meng Zhongwei，Lu Zongxiang，Song Jingyan）.中美电网的小世界拓扑模型比较分析（Comparison analysis of the small-world topological model of Chinese and American power grids）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（15）：21-24，29.

[9]曹一家，陈晓刚，孙可（Cao Yijia，Chen Xiaogang，Sun Ke）.基于复杂网络理论的大型电力系统脆弱线路辨识（Identification of vulnerable lines in power grid based on complex network theory）[J].电力自动化设备（Electric Power Automation Equipment），2006，26（12）：1-5，31.

[10]徐林，王秀丽，王锡凡（Xu Lin，Wang Xiuli，Wang Xifan）.电气介数及其在电力系统关键线路识别中的应用（Electric betweenness and its application in vulnerable line identification in power system）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（1）：33-39.

[11]邹欣，程林，孙元章（Zou Xin，Cheng Lin，Sun Yuanzhang）.基于线路运行可靠性模型的电力系统连锁故障概率评估（Cascading failure probabilistic assessment of power systems based on operational reliability model for transmission lines）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（13）：7-11，71.

[12]孙元章，程林，刘海涛（Sun Yuanzhang，Cheng Lin，Liu Haitao）.基于实时运行状态的电力系统运行可靠性评估（Power system operational reliability evaluation based on real-time operating state）[J].电网技术（Power System Technology），2005，29（15）：6-12.

[13]刘海涛，程林，孙元章，等（Liu Haitao，Cheng Lin，Sun Yuanzhang，et al）.采用瞬时概率的运行可靠性短期评估（Short-term operational reliability evaluation by using time dependent state probability）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（13）：20-25.

[14]石文辉，别朝红，王锡凡（Shi Wenhui，Bie Zhaohong，Wang Xifan）.大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法（Applications of Markov chain Monte Carlo in large-scale system reliability evaluation）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（4）：9-15.

[15]吴文可，文福拴，薛禹胜，等（Wu Wenke，Wen Fushuan，Xue Yusheng，et al）.基于马尔可夫链的电力系统连锁故障预测（A Markov chain based model for forecasting power system cascading failures）[J].电力系统自动化（Automation of Electric Power Systems），2013，37（5）：29-37.

[16]曹一家，王光增，曹丽华，等（Cao Yijia，Wang Guangzeng， Cao Lihua，et al）.基于潮流熵的复杂电网自组织临界态判断模型（An identification model for self-organized criticality of power grids based on power flow entropy）[J].电力系统自动化（Automation of Electric Power Systems），2011，35（7）：1-6.

[17]Pai M A.Energy Function Analysis for Power System Stability[M].New York：Springer，1989.

[18]刘群英，刘俊勇，刘起方（Liu Qunying，Liu Junyong，Liu Qifang）.基于支路势能信息的电网脆弱性评估（Power grid vulnerability assessment based on branch potential energy information）[J].电力系统自动化（Automation of Electric Power Systems），2008，32（10）：6-11.

Cascading Failures Forecasting Based on Importance of Component and Influence of Failure Probability

ZHENG Guo1，LI Huaqiang1，DI Tao2，ZHAO Yang1，HUANG Yan1
（1.School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China；2.Sichuan Electric Power Corporation Maintenance Company of State Grid，Chengdu 610041，China）

A new method of forecasting the following-up cascading failure is proposed to respect the real-time state and branch's importance.Firstly，a branch's failure probability model which considers the cumulative effect of power transmission is established，and weather and repair process are introduced into this model simultaneously.Secondly branch potential energy is introduced into entropy simultaneously to obtain the branch's importance considering the impact of energy transduction.Finally，a cascading failure comprehensive index is built to reflect the change of grid state and the importance of branch.Simulation results on the IEEE 30-bus system verify the validity of this model and method.

cascading failures forecasting；operation reliability；branch potential energy；entropy

TM75

A

1003-8930（2015）05-0045-06

10.3969/j.issn.1003-8930.2015.05.09

郑国（1990—），男，硕士研究生，研究方向为电压稳定及优化问题。Email：zhengguo_90@qq.com

2014-07-02；

2014-12-24

四川省科技支撑计划项目（2012GZ0009）；四川省电力公司科技项目（12H1541）

李华强（1965—），男，博士，教授，研究方向电压稳定及优化问题、电网稳定与控制研究。Email：lihq1986@hotmail.com

邸弢（1983—），男，硕士，工程师，研究方向为电压稳定及优化问题。Email：mailtotao@126.com