浅谈“全等三角形”基础图形的探究与运用
2015-07-16曹文富
曹文富

摘 要 在数学教学过程中,要关注培养学生“数学活动经验”,发展学生的数学思维,积累全等三角形的基础图形,归纳图形变换的规律,找到解决全等三角形问题的基本方法,提高解决数学问题的能力。
关键词 全等三角形 基础图形 平移 对称 旋转 变换
中图分类号:G633.6 文献标识码:A 文章编号:1002-7661(2015)05-0065-02
全等三角形是平面几何的一个基础内容,更是重要内容。运用全等三角形来证明线段相等、角相等,还可根据等角、等边进一步推出图形还具有的一些性质,如两线平行、两线垂直等。由此可以看出全等三角形这一知识所起的工具性作用。利用全等三角形解决问题的关键是要充分利用己知条件和图形结构,认真分析图形,从复杂的图形中找到一对基础三角形,弄清一个三角形是怎样通过甲移、翻折、旋转的图形变换达到另一个三角形的位置。将已知条件转化为所需的条件,弄清对应边及对应角,对照全等条件去分析己具有的条件和还缺少的条件。
由于探索三角形全等条件的方法很多,有时全等三角形会隐藏在复杂的图形中,为了能快速找到全等的三角形,因此很多同学在解题时会感到眼花缭乱,难以迅速找到对应的解题思路。只有在平时教学活动中为学生提供一个研究全等三角形的甲台,直接参与数学实践探究:如将两张纸叠起来,剪下两个全等三角形,然后将叠合的两个三角形纸片放在桌面上,从平移、对称、旋转几个方面进行摆放,看看两个三角形有一些怎样的特殊位置关系?注意两个全等三角形的对应边和对应角,让学生熟悉有代表性的位置摆放形式,为“全等三角形基础图形”的识别积累思维活动经验,让学生达到“会学”的境界。
一、基础图形类型归纳
常见的全等三角形基础图形模型有如下几种类型:
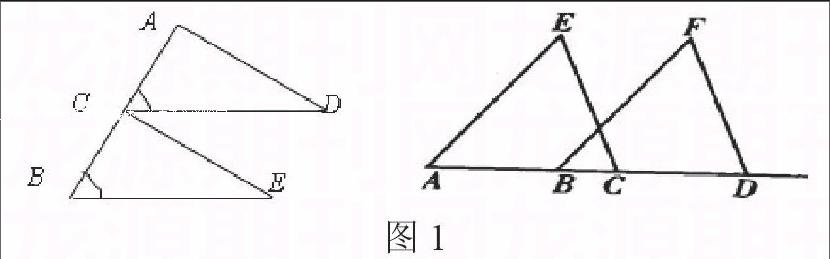
(一)平移型
如图1,此类图形可以看成有一组对应边在同一直线上的两个三角形甲移构成,故该对应边的相等关系一般可由同一直线上的线段和或差而得到。在这个基础图形中,甲行线无疑是解决问题的关键。
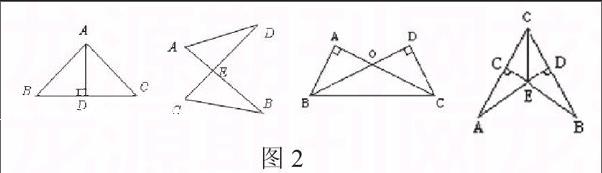
(二)对称型
如图2,此类图形的特征是两个三角形可沿某一直线翻折,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点。在这个基础图形中要注意基本的一些轴对称图形。
(三)旋转型
如图3,此类图形可以看成是绕三角形的某一顶点旋转一定角度所构成的,故一般有一对相等的角隐含在对顶角、公共角、某些角的和或差中。在这个基础图形中要注意的是一些本身具有旋转对称或中心对称性质的图形,图形的旋转不变性往往是解决问题的关键。
(四)复合型
如图4,我们在解决三角形全等问题时,经常遇到几种图形变换交替使用,综合了之前几种基本图形,例如旋转平移型、轴对称平移型等。这时就需要熟练掌握这些基本图形的特征,让学生通过实践活动发现不同问题中图形的变化规律,充分利用公共边、公共角或对顶角等特有的图形关系,可以帮助我们很快找到证明思路。
二、解决中考问题
学习数学离不开解题,会解题是学好数学的主要标志之一。全等三角形的应用在各地中考中都占有一定的比重,我们通过探索几道中考题的解法,训练学生将全等三角形的基础图形运用到具体的解题中。常见的题型有以下四类:
(一)运用平移型基础图形解决问题
案例1、(2011·玉溪中考题)如图5,点B、C、D、E在同一条直线上,己知AB=FC,AD=FE,BC=DE,探索AB 与FC的位置关系?并说明理由。
解析:由BC=DE,根据等式性质在等号两边同时加上CD,得到BD=CE,又AB=FC,AD=FE,三角形ABD与三角形FCE通过平移重合,根据SSS判定全等,由全等三角形的对应角相等可得一对同位角相等,根据同位角相等,两直线平行即可得证。
解:AB与FC位置关系是:AB∥FC,
理由:∵BC=DE(已知),
∴BC+CD=DE+CD(等式的基本性质),即BD=CE,
在△ABD和△FCE中,
∴△ABD≌△FCE(SSS),
∴∠B=∠FCE(全等三角形的对应角相等),
∴AB∥FC(同位角相等,两直线平行).
(二)运用对称型基础图形解决问题
案例2、如图6,已知四边形纸片ABCD中,AD∥BC,将∠ABC,∠DAB分别对折,如果两条折痕恰好相交于DC上一点E,点C,D都落在AB边上的F处,你能获得哪些结论?
解析:利用图形对折前后重合部分全等,从线段关系、角的关系、面积关系等不同方面进行探索,以获得更多的结论,是一道开放性试题。
解:①AD=AF,ED=EF=EC,BC =BF.
②AD十BC =AB,DE+EC =2EF.
③∠1 =∠2,∠3 =∠4,∠D=∠AFE,∠C=∠EFB,∠DEA =∠FEA, ∠CEB =∠FEB.
④∠AEB=90。或EA⊥EB.
⑤S△DAE=S△EAF,S△ECB=S△EFB.
【思考】本题融操作、观察、猜想、推理于一体,需要具有一定的综合能力,推理论证既是说明道理,也是探索、发现的途径,善于在复杂的图形中发现、分解、构造基本的全等三角形是解题的关键,需要注意的是,通常面临以下情况的图形中没有全等三角形,而证明结论需要全等三角形.(2)从题设条件中无法证明图形中的三角形全等,证明需要另行构造全等三角形。
(三)运用旋转型基础图形解决问题
案例3、(玉溪中考题).如图7,己知AB=AD,∠1=∠2,要使△ABC≌△ADE,还需添加的条件是(只需填一个)
。
解析:因为∠1=∠2,∠DAC为公共角,易得∠BAC=∠DAE,将△ABC绕A点旋转可以与△ADE对应重合,从而确定对应边和对应角,所以可添加∠B=∠D或∠C=∠E或AC = AE
三、运用复合型图形解决问题
案例4、(2012年云南省中考题)如图8,在△ABC中,∠C = 90。,点D是AB边上的一点,DM⊥AB,且DM =AC,过点M作ME//BC交AB 于点E求证:△ABC≌△MED
解析:(平移旋转对称型)如图,根据已知条件DM =AC,∠C =90。和DM⊥AB,不难看出△ABC和△MED之间可以通过平移、旋转、轴对称三种变换而互相重合,从而容易寻找全等的条件。
证明:∵ME//BC
∴∠DEM = ∠B(两直线平行,同位角相等)
∵DM⊥AB→∠MDE = 90。=∠C
在△ABC和△MED中
通过运用基础图形解决以上全等三角形的中考题可以看出,从学生已有的知识储备和现有的认知基点出发,通过实践操作活动,将学生紧紧拴牢在数学思维活动这一具有数学本质的维度中。这不仅有助于我们对全等三角形知识的理解和记忆、加深巩固全等三角形的知识,又发展了图形变换的思维,把数学知识转化为数学能力。与此同时,能对学生有效地进行数学思维训练,而且还能为学生积累基本的数学活动经验,提供有效的活动载体,培养学生主动探索的创造性能力,进而全面提高学生应用知识解决问题的能力。
