Mathe matica软件在物理教学中的应用——以黑体辐射有关公式为例

李寅杰 徐 慧

（南京师范大学附属中学 江苏 南京 210003）

1 引言

在物理教学中，在讲解一些具有复杂表达式的物理问题时，常受限制于学生当前的知识水平，只能一带而过，导致学生对知识死记硬背，理解浅显.Mathematica是Wolfram公司开发的科学计算软件，具有强大的数值计算能力［1］.利用 Mathematica软件可解决数学计算的困难，还可以得到直观的图像，让很多复杂问题清晰直观，使学生轻松、深入地理解物理概念、公式.本文以黑体辐射中的普朗克公式为例，通过数值拟合和符号运算，验证在低频率范围与瑞利-金斯公式的符合度问题.

2 正文

2.1 概述

瑞利-金斯公式是由英国物理学家瑞利和金斯提出，用于描述黑体辐射问题光谱能量分布，表达式为

其中ρ为热辐射能量密度，ν为热辐射频率，T为热力学温度，c为真空中光速，h为普朗克常量，k为玻尔兹曼常数.该公式在长波区域与实验符合较好，但在短波区域，会导致能量无限大的荒谬结果，也就是当时著名的“紫外灾难”.

普朗克公式是德国物理学家普朗克提出，用于描述黑体辐射问题光谱能量分布的公式.表达式为

其中ρ为热辐射能量密度，ν为热辐射频率，T为热力学温度，c为真空中光速，h为普朗克常量，k为玻尔兹曼常数.这一公式弥补了之前瑞利-金斯公式和维恩位移定律的不足，与实验吻合度高.

我们利用Mathematica软件进行模拟时，为了使数据直观且便于输入，取能量的单位为10－20J，频率ν的单位为1013Hz，热力学温度T的单位为100 K，普朗克常量h取6.626 069 572 9×10－34J·s［2］，光速c取299 792 458m·s－1［3］，玻尔兹曼常数k取1.380 648 813×10－23J·K－1［4］.代入数据后，普朗克公式的表达式可写为

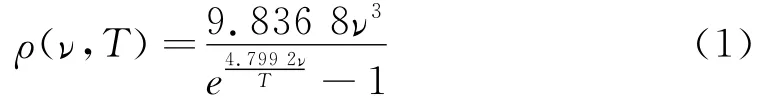
2.2 数值模拟

将式（1）输入，证明普朗克公式在低频率区域转化为瑞利-金斯公式，按照普朗克公式在低频率区域取值后，可以拟合为瑞利-金斯公式.首先考虑温度为100K的情况，取温度为1，从ν＝0.000 1开始，每次间隔0.000 1，一直到0.002，取点.得到

（0.000 1，2.049 18×10－8）

（0.000 2，8.194 77×10－8）

（0.000 3，1.843 38×10－7）

（0.000 4，3.276 33×10－7）

（0.000 5，5.118 04×10－7）

（0.000 6，7.368 21×10－7）

（0.000 7，1.002 65×10－6）

（0.000 8，1.309 28×10－6）

（0.000 9，1.656 65×10－6）

（0.001 0，2.044 76×10－6）

（0.001 1，2.473 57×10－6）

（0.001 2，2.943 04×10－6）

（0.001 3，3.453 16×10－6）

（0.001 4，4.003 88×10－6）

（0.001 5，4.595 19×10－6）

（0.001 6，5.227 05×10－6）

（0.001 7，5.899 43×10－6）

（0.001 8，6.612 30×10－6）

（0.001 9，7.365 64×10－6）

（0.002 0，8.159 42×10－6）

由于瑞利-金斯公式的形式为ρ～Tν2，所以我们对这些数据用二次函数拟合.将散点和拟合出的函数绘制出，并显示在同一坐标系中，可以清晰地看出，完美符合二次曲线，如图1所示.（在这里Mathematica为了使图像美观，将y轴右移，实质上该图像ν≥0.）

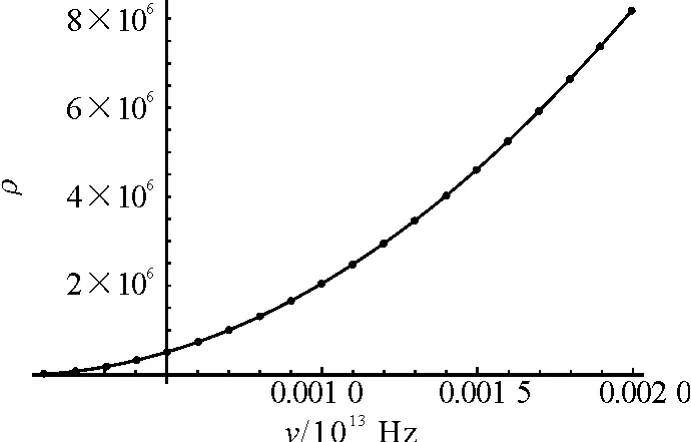
图1

我们依次考虑温度为300K，500K，900K和1 000K的情况，代码与之前几乎相同，拟合的结果为：

300K：R＝－2.610 7×10－9＋

1.332 26 ×10－5ν＋6.133 54ν2

500K：R＝－2.611 68×10－9＋

1.332 71 ×10－5ν＋10.232 9ν2

700K：R＝－2.612 1×10－9＋

1.332 9 ×10－5ν＋14.332 2ν2

900K：R＝－2.612 33×10－9＋

1.333 01 ×10－5ν＋18.431 6ν2

1 000 K：R＝－2.612 41×10－9＋

1.333 04 ×10－5ν＋20.481 3ν2

我们着手进行两公式的转化，观察不同温度下R函数，一次项系数、常数项的数量级与二次项系数的数量级相差巨大，而且瑞利-金斯公式中只含二次项，故舍去常数项和一次项.现在R函数与瑞利－金斯公式在形式上相一致，只需验证二次项系数.由于二次项系数与T成正比，所以对R函数的系数与温度（表1）进行线性拟合.

表1 函数的系数与温度值

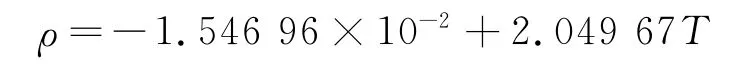
由于一次项系数远大于常数项，故舍去常数项，Rho＝2.049 67t.这与现在单位制下的瑞利-金斯公式：ρ＝2.049 66Tν2，几乎完全相同，由此可知，普朗克公式在长波区域可转化为瑞利-金斯公式.

而当我们将散点范围增大时，可见到在高频区域，二者出现较大偏差.取温度为1，ν＝0.000 1开始，每次间隔0.01，一直到0.2，取点.将瑞利-金斯公式的图像和普朗克公式的散点绘出，并显示在同一坐标系中，得到图2.清晰地看出，在短波区域，二者的差别不断增大.

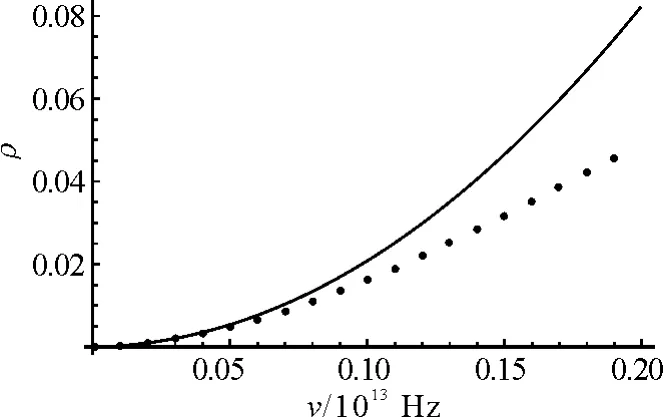
图2

3 反思

观察数值模拟的数据，在第6位有效数字处与公式不同，分析原因及改进措施：

（1）Mathematica使用过程中分布计算，导致第一步保留的有效数字不足.应当一次性键入算式，只保留一次有效数字.

经过验证，由于Mathematica本身可以储存较多位数，所以对于此处的5位小数结果，是否一步计算并无差别.

（2）在二次拟合时选用了ax2＋bx＋c的形式，可以尝试使用ax2，ax2＋bx，ax2＋c等形式，看是否可以减少误差.在线性拟合时选用了kx＋b的形式，可以尝试使用kx形式，看是否可以减少误差.

经过验证，当选择ax2和kx时，得到的结果是2.049 66T，确实可以减少误差.我们从中可以受到启发，既然是验证性质的，就可以根据已知进行尽量精确的拟合，这样才能提高结果的准确性.

4 总结

Mathematica具有清晰、直观的特点，可较好地演示.同时其拥有强大的计算、绘图功能，可以快速、准确地完成计算和推导.对于一些难以计算、推导过程的知识点，Mathematica的使用可能会带来意想不到的效果.在科学飞速发展的今天，Mathematica为物理教学开辟了一条新思路.

1 https：∥zh.m.wikipedia.org／wiki／Mathematica

2 http：∥ physics.nist.gov ［Thursday，02－Jun－2011 21：00：12EDT］. National Institute of Standards and Technology，Gaithersburg，MD 20899

3 Penrose，R （2004）.The Road to Reality：A Complete Guide to the Laws of the Universe.Vintage Books.pp.410－1.ISBN 978－0－679－77631－4

4 http：∥physics.nist.gov／constants ［Thursday，02－Jun－2011 21：00：12EDT］. National Institute of Standards and Technology，Gaithersburg，MD 20899