轻绳模型之竖直面内圆周运动条件分析
2015-07-14陈学刚
陈学刚
(重庆市梁平中学 重庆 405200)
在学习了汽车过拱桥和凹桥的圆周运动实例之后,教师们都会给出这样一个情境:一轻绳一端拴一可视为质点的小球,轻绳长R,使小球绕轻绳的另一端在竖直面内做圆周运动.分析小球在竖直面内做圆周运动所满足的条件.
通常在最高点对小球进行动力学分析得出(受力分析如图1)
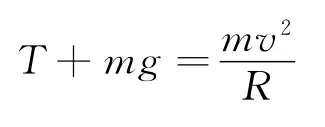
从上式看得出来,速度越小,绳子的拉力将越小.由于绳子只能是拉力,所以绳子的最小拉力为零.于是有
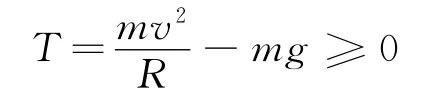
解得
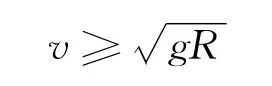
于是进一步给出结论:小球恰好能在竖直平面内做圆周运动的条件是在最高点的速度为.然而这一结论对于初学者来说接受起来非常困难.教学过程中学生提出了一些问题促使笔者做出本文完善了上述推导,并提出了更合理的解决办法.
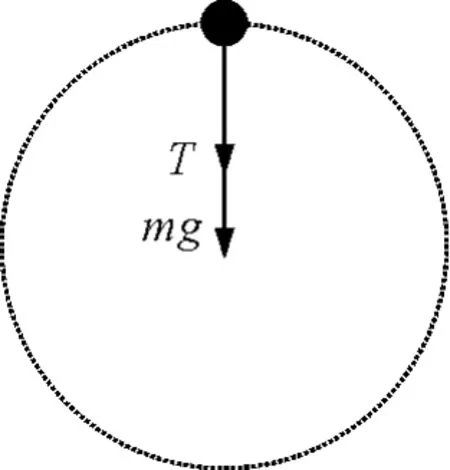
图1
1 问题分析
教学过程中学生的困惑基本上有两点:
其一,前面的推导只得出了我们想当然的圆周运动“最高点”处的最小速度而当小球在“最高点”的速度时,小球在竖直面内一定做的是圆周运动吗?
其二,最高点处的速度为什么就不能等于零?
2 问题解决
2.1 从运动学角度分析

图2
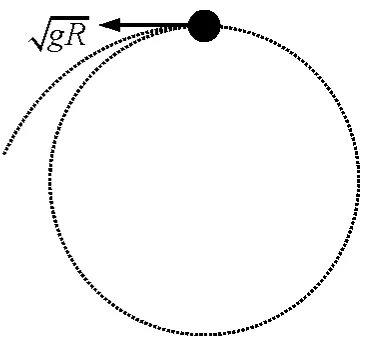
图3
以最高点为原点作正交坐标系,建立方程
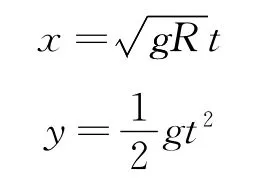
计算运动过程中小球与圆心的距离

由于轻绳不可伸长,小球在绳子的约束下只能沿圆周往下运动.
如图2,设小球从右边往上运动至最高点,若是从圆周上的某点在圆内斜抛而上,那么根据斜抛运动的对称性可知,左边的运动将是平抛,与前面的推证不符,所以不可能是从圆周上的某点斜抛而上至最高点,而只能是沿圆周而上,再次到达最高点速度变为(这一过程是满足机械能守恒条件的).换言之,小球在圆周最高点的速度为时,小球在竖直平面内做的是圆周运动,从而解决了学生的第一个问题.
2.2 从动力学角度分析
有一个事实我们很容易想到,在上述情境中若是小球做圆周运动,那么绳子将一直被拉直.因为做圆周运动需要向心力,除在最高点重力(指向圆心)完全用来提供向心力而可以不需绳子拉力外,其他地方就必须有指向圆心的绳子拉力才行.我们可以假设小球在最高点速度为时能够保持圆周运动,若能证明除最高点外绳子处处有拉力即可.如图4所示,设小球处在任意一点,绳子对小球的拉力为T,则

以最高点为零势能点
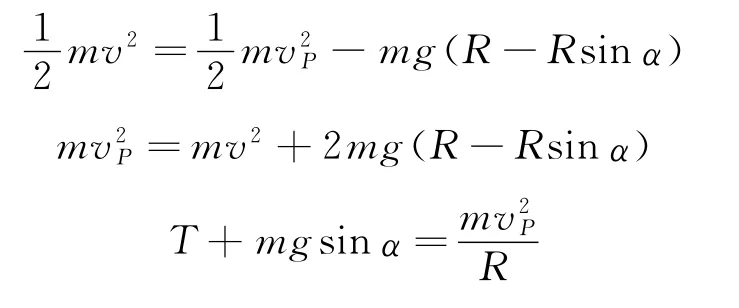

图4
由上式可得

当0≤α≤360°,有-1≤sinα≤1,则

始终成立,其中α=90°,即小球在最高点时,T=0.于是我们的假设得到证明.
以上两种方法相当于是对轻绳模型情况下小球在竖直面内做圆周运动的临界条件的完善.前面提出的结论之所以不让人信服而需要补充说明是因为得此结论时我们从特殊位置去突破的,这种情况以点代面,以偏概全,缺乏说服力.下面的方法将从任意位置着手,做一个比较严密的推导.
2.3 小球竖直面内做圆周运动条件的推证
我们想象小球是从最低点以某一速度开始运动,P点是小球在圆周上的某一点,对其进行受力分析(如图4),根据向心力公式有
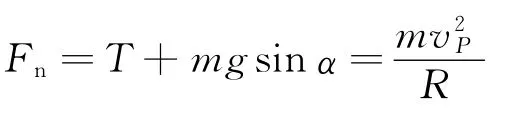
变形后
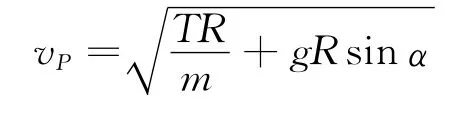
因为小球要能在图示虚线轨迹上做圆弧运动,在任意点P绳子必须是拉直或拉紧的,所以有T≥0.角度α决定了小球的位置.
当小球在第三、四象限(180°≤α≤360°)时内,由vP≥0有
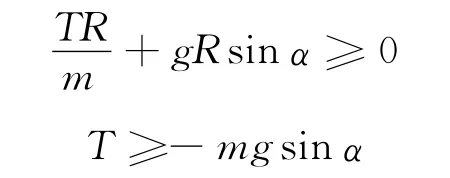
又因为此时,-1≤sinα≤0,所以有T≥0恒成立,即小球在三、四象限不可能有脱离圆轨的情况.
当小球在第一、二象限(0<α<180°)时,若小球刚好能上到P点,因为
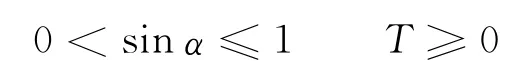
则
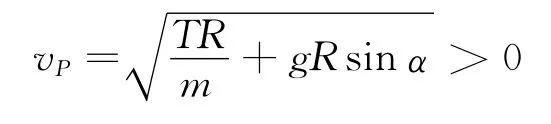
恒成立,也就是这个范围小球的速度不可能为零.
当小球“恰好”能上到P点(此时P点不是最高点),在P处绳子将会松弛,意味着T=0,得到小球在P点这个位置的最小速度.由于绳子开始松了,绳子拉力不存在了,恒定的重力将使小球做抛体运动,轨迹是抛物线.P点越靠近最高点,sinα的值越大,vPmin就越大,而不是趋于零.学生的第2点疑惑在这儿得到解决.
当P点就是最高点时,那么sinα=1,小球在最高点最小速度

至此我们才可以得出这样的结论:(轻绳模型下)小球“恰好”能在竖直面内做圆周运动,则最高点的速度必然是或者小球若能上到圆周最高点,则到达最高点的速度至少为
