科学推理能力在物理问题表征过程中的作用

陈敏丽 熊建文 肖 洋

（华南师范大学 广东 广州 510006）

1 引言

我国2006年版的《普通高中物理课程标准（实验）》和2011年修订的《义务教育物理课程标准》，在“课程目标”、“内容标准”和“实施建议”中明确提出了要以培养学生的科学探究能力为宗旨，以“提高学生的科学素养”为核心目标，科学探究对学生科学素养的发展具有不可替代的作用.科学探究是指个体通过自主地调查和研究来认识和解释自然的过程［1］.国内外科学教育研究者普遍认为科学探究没有固定的形式，但是却有一些可辨别的要素：提出问题、猜想与假设、设计实验、进行实验与收集数据、分析与验证、得出结论、反思评价、拓展迁移加参考文献，而科学推理能力则是整个过程中最核心的部分.

自20世纪60年代以来，皮亚杰基于认知发展理论提出的科学推理（Scientific Reasoning）就引起了国内外科学教育研究者的关注，并被认为是学生科学探究能力的重要组成部分.研究者们认为：科学推理（Scientific Reasoning）是个体思维能力发展到一定高度之后具有的推理类型；在个体进行科学推理时一般采用的推理类型是归纳推理和演绎推理；个体应用科学推理进行假设检验或问题解决.同时科学推理能力的测试可以从7个维度进行：守恒推理能力、比例推理能力、控制变量推理能力、概率思维能力、相关性思维能力以及假设演绎推理能力.Lawson等 人 研 究 开 发 出 的 《Lawson′s Classroom Test of Scientific Reasoning》［2］即 LCTSR 测试量表已被广泛用于对科学推理能力的调查研究当中［3］.

基于以上分析，我们发现，研究者们普遍认为“个体应用科学推理进行假设检验或问题解决”，即科学推理与问题解决有着一定的联系.但文献［4］的研究却表明学生的物理知识与科学推理能力的相关性不大，文献［5］的研究也发现科学推理能力与物理问题解决能力不相关.但他们的研究中对学生物理问题解决能力评价均以最终的总成绩来衡量，缺乏对物理问题解决过程的动态关注，也缺乏对科学推理的各个维度与物理问题解决过程的深入分析.

问题解决是一个动态的过程，文献［6］认为问题表征（Problem Representation）是问题解决的一个中心环节，问题表征的正确与否，很大程度上影响了问题解决的结果.也就是说，问题能否顺利解决，问题表征起着关键作用.McDermott和Larkin认为物理问题解决通常经历4个表征步骤：文字表征、朴素表征、科学理论表征、数学表征.文献［7］对物理问题表征各个环节作出了详细的说明：文字表征仅仅是问题的文字理解；朴素表征是物理情境的草图，它使问题更显而易见，更可视化；科学理论表征包括所有能被用来解决问题的、反映物理实质过程的量，如力和动量，但不包括现实生活中的实际物体，如物块和绳子，在力学问题上，科学理论表征常常体现为物体受力分析的图式构建；数学表征则是一系列的公式，它在科学理论表征的基础上建立出来，并且可直接被用以问题答案的求解.文献［8］进而对各表征层次有以下界定：文字表征所占时间，开始读题至读毕；朴素表征所占时间，开始画图到画图毕或读题毕；物理表征所占时间，第一次物理词汇出现至不再有新的物理概念或原理出现前；数学表征所占时间，第一个数学公式出现时刻至数学推导完毕.

因此，我们希望借鉴文献［8］的物理问题解决的表征体系，研究科学推理能力与物理问题解决动态表征过程的关系.

2 研究方法

2.1 实验材料

实验材料包括《Lawson′s Classroom Test of Scientific Reasoning》和自编的《高一学生物理问题表征能力测试量表》.

《Lawson′s Classroom Test of Scientific Reasoning》由多位相关专业的研究生翻译，经历多次校对与修改，在维持题目测量目的不变的条件下，以确保能让中国学生流畅阅读.

《高一学生物理问题表征能力测试量表》则是在《普通高中物理课程标准》的要求下根据相关物理教材，在重点中学物理教师的帮助下，确定了测试的知识内容，其中涵盖直线运动、平衡问题、牛顿运动定律、平抛运动、圆周运动等内容.针对每个知识点选取3～4道问题，通过对112位高一学生的预测，筛选出区分度大、难度中等的问题.在确定题目之后，结合文献［7］和文献［8］对物理问题各表征层次的界定，设置问题的结构.各表征层次并不相互独立，在设计问卷的过程中应考虑到各表征层次的交叠.

各层次计分编码如下：文字表征层次的得分P1即 “关键词”一项的得分；朴素表征层次的得分P2即 “画草图”一项的得分；科学表征层次的得分P3即 “画草图”和“确定思路”两项的得分；数学表征层次的得分P4即“确定思路”和“求出最后答案”两项的得分.

2.2 程序

在广州市某中学根据学生平时成绩，通过分层抽样的方式选取被试共72人，学优生、中等生和学困生各24人.

通过问卷调查法，以 《Lawson′s Classroom Test of Scientific Reasoning》和《高一学生物理问题表征能力测试量表》作为测量工具，对被试集中进行独立测试.测试不限制时间，直到学生完成为止.

利用Spss19软件对数据进行处理.

3 结果

被试学生有72位，所得测试结果为72份，剔除无效问卷15份，最终所得的有效结果为57份.

《LCTSR测试量表》中各个科学推理能力的维度所对应的题目及被试各个维度得分统计如表1所示.

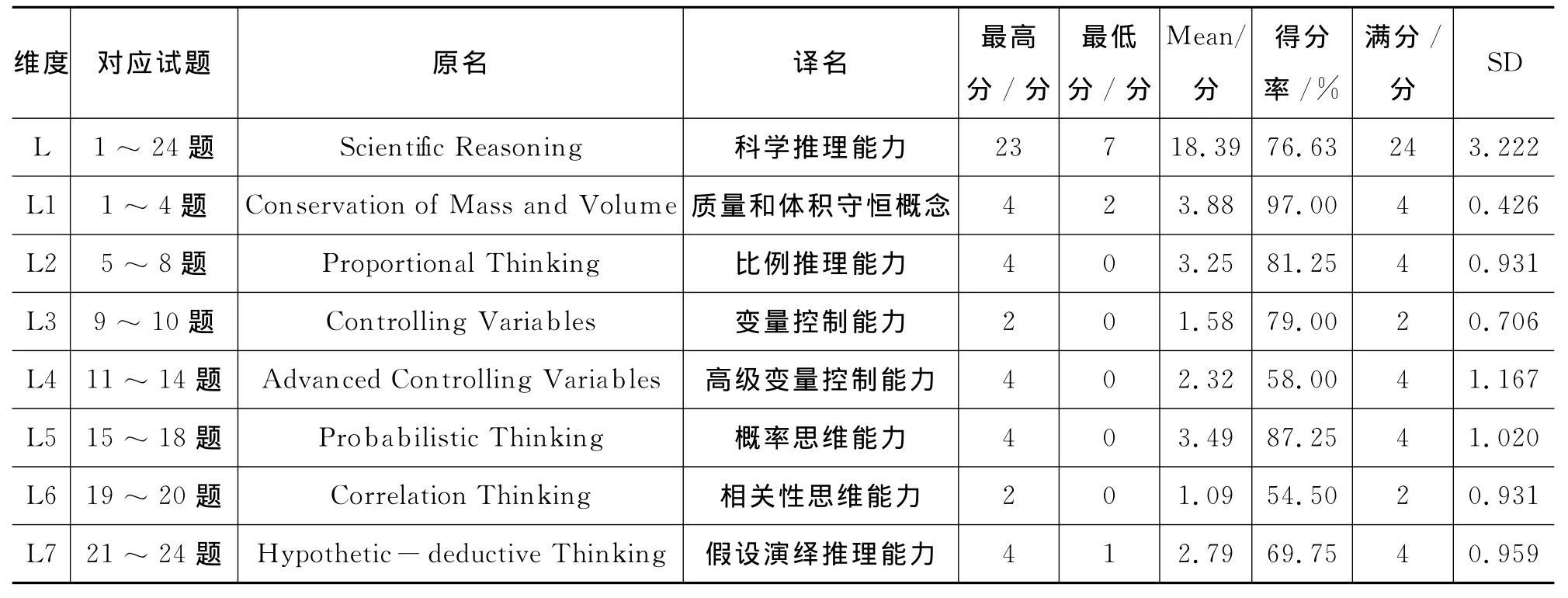
表1 LCTSR测试7个维度统计结果

被试各个维度能力发展不平衡，质量和体积守恒概念能力（L1）的平均得分率非常高，为97.00%，概率思维能力（L5）平均得分率为87.25%，比例推理能力（L2）和变量控制能力（L3）的平均得分率也较高，分别是81.25% 和79%，假设演绎推理能力（L7）的得分率为69.75%，高级变量控制能力（L4）和相关性思维能力（L6）的得分率比较低，分别是58.00% 和54.50%.

《高一学生物理问题表征能力测试量表》测试统计结果如表2所示.

被测的物理问题表征能力测试结果数据的峰度系数（－0.685）与其标准误差（0.623）的比值，偏度系数（0.622）与其标准误差（0.316）的比值都小于2，可近似认为该变量符合正态分布.表中的得分率和标准偏差也显示，问卷的难度中等、区分度大.

被试的科学推理能力与物理问题表征能力的相关性分析结果如表3所示.

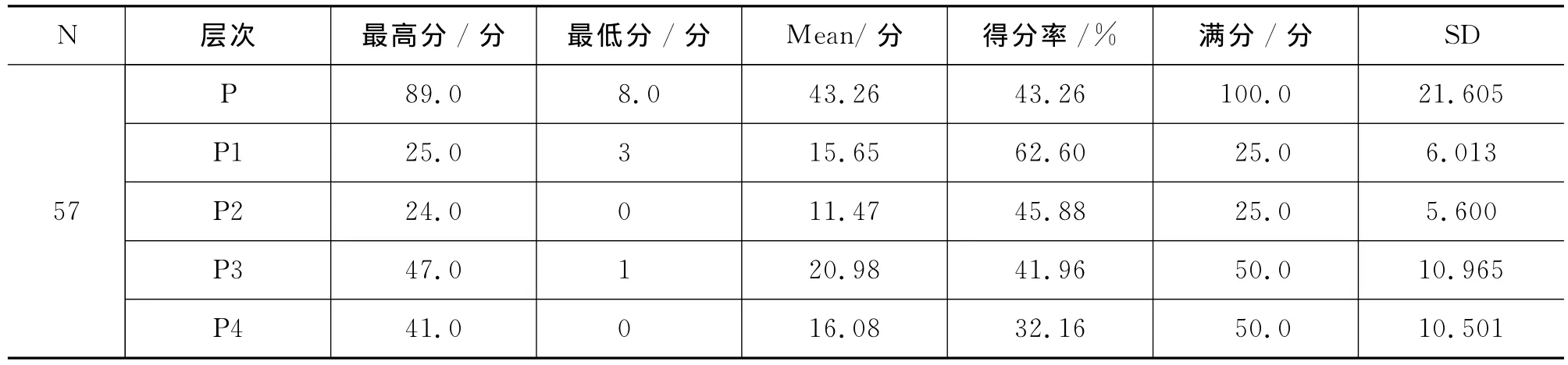
表2 物理问题表征能力测试统计结果

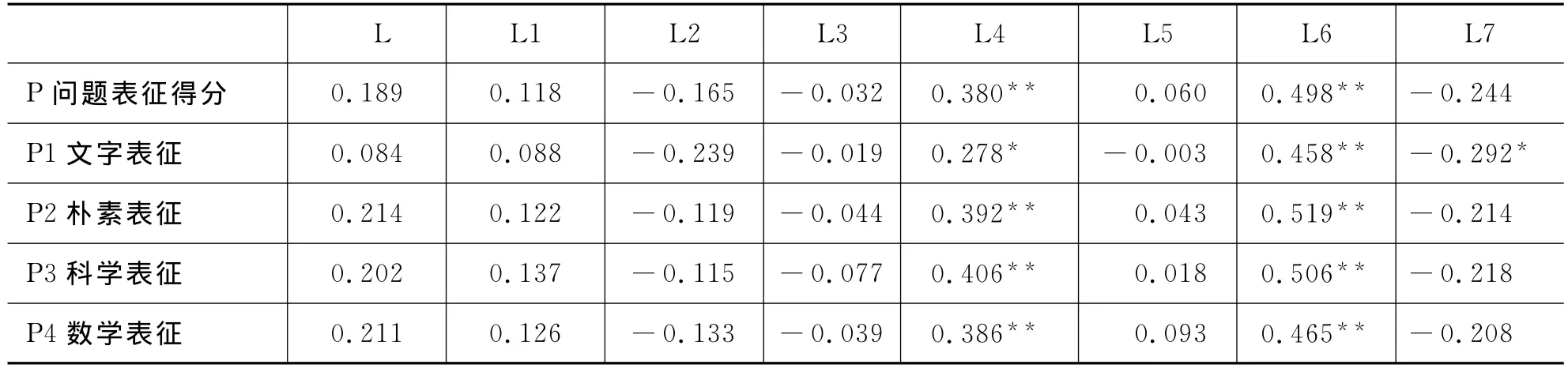
表3 物理问题解决与科学推理描述性统计与相关性分析

数据处理结果显示，科学推理能力测试总成绩与物理问题表征能力测试总成绩的相关系数∣r∣＝0.189，p＞0.05.虽然相关性达到了显著性水平，但是相关系数非常小，所以，我们可以认为科学推理能力与物理问题表征能力整体呈现不相关关系，这与以往国内外的研究结果一致.

高级变量控制能力（L4）与物理问题整体表征能力以及各表征层次能力的相关性均显著，p＜0.05.相关性思维能力（L6）与物理问题整体表征能力以及各表征层次能力的相关性均显著，p＜0.01.假设演绎推理能力（L7）虽然与物理问题整体表征能力和大部分问题表征过程不相关，但与文字表征能力（P1）之间显著相关，p＜0.05.

3.1 高级变量控制能力与物理问题表征能力的统计分析

以上是对科学推理能力与物理问题表征能力的相关性分析，下面我们着重探讨不同科学推理能力对物理问题整体表征能力及各层次表征能力的影响.

首先以物理问题整体表征得分（P）、文字表征（P1）、朴素表征（P2）、科学表征（P3）和数学表征（P4）为因变量，高级变量控制能力（L4）为自变量进行多因素方差分析.结果显示，不同高级变量控制能力（L4）下物理问题整体表征得分（P）存在显著差异，F（4，52）＝2.913，p＝0.030.从物理问题表征各个层次来看，不同高级变量控制能力的被试，他们的朴素表征（P2）、科学表征（P3）和数学表征（P4）3个表征层次的能力都存在显著差异，［F（4，52）＝2.970，p＝0.028］，［F（4，52）＝ 3.298，p＝ 0.018］，［F（4，52）＝3.182，p＝0.021］，而文字表征层次（P1）没有存在显著差异［F（4，52）＝1.861，p＝0.131］.

3.2 相关性思维能力与物理问题表征的统计分析

以物理问题整体表征得分（P）、文字表征（P1）、朴素表征（P2）、科学表征（P3）和数学表征（P4）为因变量，相关性思维能力（L6）为自变量进行多因素方差分析.结果显示，不同相关性思维能力下物理问题 整体表征能力（P）存在极显著差异，F（2，54）＝8.888，p＝0.000，而不只是相关的关系.将物理问题表征分层次来看，不同相关性思维能力（L6）的被试，他们的文字表征（P1）、朴素表征（P2）、科学表征（P3）和数学表征（P4）4个表征层次的能力均存在极显著差异，［F（2，54）＝7.258，p＝0.002］，［F（2，54）＝10.014，p＝0.000］，［F（2，54）＝9.271，p＝0.000］，［F（2，54）＝7.485，p＝0.001］.

4 讨论与建议

与以往的研究结果一致，本文发现科学推理能力与物理问题表征能力整体不相关.但是深入分析发现，科学推理能力中的高级变量控制能力和相关性思维能力两个维度与物理问题表征的各个层次不仅仅是相关的关系，因为不同高级变量控制能力和相关性思维能力的被试在各个表征层次都存在显著差异.我们认为，在问题解决的过程中学生有时需要应用控制变量法，通过人为地控制一些影响事件变化的条件，使得其中一些变量或因素不发生变化或依照需要发生变化从而可以更好地找到事物变化的规律，更好地解决问题.变量控制能力最重要的是掌握控制变量法并且应用它来解决多个变量之间的关系和问题［9］.而相关性思维是一种非常重要的科学思维方式，事物的因果关系总是源自于他们的相关关系［10］.已有研究也表明，相关性思维能力有利于学生对函数和自变量之间关系的建立，对于学生学习自然科学非常关键［11］，并且多数物理量之间也都存在着函数关系.可能是由于这种原因，学生的高级变量控制能力和相关性思维能力对物理问题表征过程存在影响.

相比物理问题解决过程中的朴素表征、科学表征和数学表征3个层次，人们可能认为文字表征层次的能力与科学推理能力关系不大.在物理问题表征过程中，文字表征要求个体掌握与描述事件相关的知识和语词，主要与问题解决者对问题本身的文字描述有关.三段论中的气氛效应理论中提到，前提的性质和量词会在推理者心目中形成一定的氛围［12］；三段论中的心理模型理论也提到推理者在推理的时候首先会构成一个由前提中所描述事件的知觉或表象的心理模型［13］.所以，文字表征能力必然对科学推理过程有影响.而基于本论文的研究，学生的某些科学推理能力的维度（相关性思维能力）也显著影响其文字表征能力.

教师们应该坚持提高学生科学探究能力的理念，因为提高学生在科学探究过程中的科学推理能力非常重要.科学探究过程是基于对整个自然界和人类社会的好奇，可以给予人类无限的活力，并时时刻刻改变着我们的世界，让我们得到更多的知识.结合相关的研究和本论文的研究可以看到，虽然从整体上看来科学推理能力对物理问题整体解决能力似乎没有什么关系，但是关注物理问题解决的动态过程的时候发现，学生在某些维度的科学推理能力对其物理问题解决能力还是有作用的.在培养学生科学推理能力的过程中，高级变量控制能力和相关性思维能力两个维度必须引起重视，因为这两方面的能力对学生解决物理问题过程中通过观察、实验、阅读等收集证据之后结合已有知识体系而发现新信息、合成新知识可能有非常重要的作用.

另外，本研究显示科学推理能力中只有高级变量控制能力和相关性思维能力这两个维度会对物理问题的解决过程产生作用，从LCTSR测试7个维度的统计结果发现这两个维度试题的得分率分别为58.00% 和54.50%.高级变量控制能力（L4）满分为4分，标准差（SD）为1.167；相关性思维能力（L6）满分为2分，标准差（SD）为0.931.得分率适中，标准差较大显示这两个维度的试题对该测试群体而言难度中等，区分度较大.虽然《Lawson′s Classroom Test of Scientific Reasoning》在国外适合于用来测试科学推理能力，但是细读时却发现该量表的许多题目对于长期接受解题训练的中国学生来说难度过小.从表1可以看到许多维度的得分率过高，标准差较小，即难度低，区分度不大.所以运用该量表进行科学推理能力的测试时需要进行改编，而科学推理的其他维度是否真的对物理问题解决能力没有作用仍是一个需要深入研究的问题.对于文献［4］研究得出的学生的物理知识与科学推理能力的相关性不大的结论，以及文献［5］研究发现的科学推理能力与物理问题解决能力不相关的结果也值得进一步研究.

5 结论

科学推理能力与物理问题表征能力整体不相关，但科学推理能力的高级变量控制能力和相关性思维能力对物理问题表征过程存在显著影响.

1 陈琴，庞丽娟.科学探究：本质、特征与过程的思考.教育科学，2005（2）

2 Lawson A E.Classroom test of scientific reasoning.Arizona State University，2000

3 严文法，胡卫平.国外青少年科学推理能力研究综述.外国中小学教育，2009（5）：23～28

4 Bao L，Cai T，Koenig K，et al.Learning and scientific reasoning.Science，2009，323（5914）：586～587

5 艾彤，邢红军.科学推理能力与物理问题解决能力的对比研究：［学位论文］.北京：首都师范大学，2013

6 Newell A，Simon H A.Human problem solving.Englewood Cliffs，NJ：Prentice－Hall，1972

7 Larkin J.Cognition of learning physics.American Journal of Physics，1981，49（6）：534～541

8 廖伯琴，黄希庭.口语报告法比较研究物理问题解决中不同数理基础被试表征体系的动态差异.心理发展与教育，1999（4）：31～34

9 皮亚杰.皮亚杰发生认识论文选.上海：华东师范大学出版社，1991.4

10 陈健.科学划界的多元标准 .自然辩证法通讯，1996，18（3）：8～15，37

11 AdiH， KarplusR，Lawson A E.Development of Correlational Reasoning in Secondary Schools： Do Biology Courses Make a Difference？ The American Biology Teaeher.1979，41（7）：420～425

12 Woodworth，R.S.＆Sells，S.B.（1935）.An Atomosphere Effect in Form Syllogistic Reasoning， Journal of ExperimentaL Psychology，18，451～460

13 毕鸿燕，方格.演绎推理的心理模型理论及相关研究.心理科学，2001，24（5）：595～596