LiMgPbSb 型四元Heusler 合金CoFeTiSb 的半金属性及其无序效应

张远强，冯 雨，高钦翔，黄海深

(1. 遵义师范学院物理与机电工程学院，遵义563002;2. 西南大学物理科学与技术学院，重庆400715)

1 引 言

半金属铁磁材料(half - metallic ferromagnetism)是一类具有特殊能带结构的材料，它的一个自旋子能带穿过了费米面，呈现出典型的金属特征;而另一个自旋子能带在费米面处存在一个明显的带隙，呈现出典型的半导体性. 这种独特的能带结构使得半金属铁磁材料在费米面处具有100% 的自旋极化率，因此在磁传感器，自旋阀，隧道结等自旋相关器件中具有巨大的应用前景［1-6］. 自从1983 年de Groot 等人首次采用密度泛函理论预测了Heusler 合金NiMnSb 具有半金属性以来［7］，越来越多的Heusler 合金被证实为半金属铁磁体，得到了人们极大的关注. 对化学式为X2YZ (X，Y 一般为过渡金属元素，如Ni，Fe，Mn，Co，Cr，Ti 等，Z 一般为主族元素，如Si，Al，Ga，Ge，Sn，Sb 等)，空间群为FM -3M 的Cu2MnAl 型 Heusler 合 金， 如 Co2MnSi［8］，Co2FeSi［9］等，由于具有高于室温的居里温度，以及满足于Slater -Pauling 规律(Mt=Zt-24，Mt为合金总磁矩，Zt为总价电子数)的总磁矩，得到了人们极大的青睐. 除了传统的Cu2MnAl 型Heusler合金之外，具有化学式为X2YZ (两个X 原子处于不等价的空间位置)，空间群为F - 43M 的Hg2CuTi 型 Heusler 合 金， 如 Ti2NiAl［10］，Ti2CoAl［11，12］等，也是人们研究的热点，并且展现出良好的发展潜力. 然而，人们探索Heusler 合金的脚步并未停止. 最近，一些新奇的四元Heusler合金，即 LiMgPbSb 型 Heusler 合 金，例 如CoFeMnZ (Z = Al，Ga，Si，Ge)［13］，Ni(CoFe)MnGa［14］，CoFeCrZ (Z = Al，Si，Ga，Ge)［15］，已被证实具有半金属性. 如图1 所示，LiMgPbSb型Heusler 合金具有化学式XX’ YZ，其中X，X’，Y 为三种不同的过渡金属元素，其中X 空间坐标为(0.5，0.5，0.5)，X’空间坐标为(0，0，0)，Y 空间坐标为(0.25，0.25，0.25);Z 为主族元素，空间坐标为(0.75，0.75，0.75). 由于LiMgPbSb 型Heusler 合金已被证实具有较低的磁矩和较高的居里温度，因此值得人们进一步的探索.

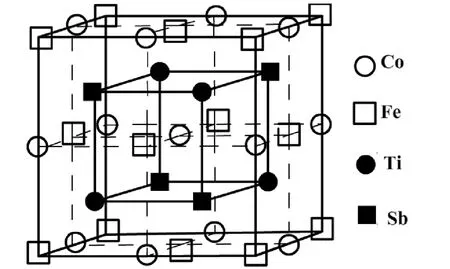
图1 Heusler 合金CoFeTiSb 的结构示意图Fig. 1 Schematic demonstration of the structure of Heusler alloy CoFeTiSb

然而，一些Heusler 合金虽然通过第一性原理计算被预测具有半金属性，但它们100% 自旋极化率却在实验中不易检测到. 究其原因，一种最大的退极化可能性就原子无序效应［16，17］. 中子衍射实验证明，Cu2MnAl 型Heusler 合金Co2MnSi的自旋极化率为55% 而不是理论预测的100%.造成自旋极化率下降的主要原因是在Co2MnSi 块体中，有5% -7% 的Co 原子被Mn 原子替代，而14% 的Mn 原子被Co 原子替代，显示出强烈的Co - Mn 交换无序［18］. 此外，对Hg2CuTi 型Heusler 合金Ti2FeAl 的研究表明［19］，无序效应会造成自旋极化率的大幅下降，从而严重影响Heusler 合金在实际中的应用. 基于这个原因，研究无序效应对Heusler 合金的半金属性影响是非常必要. 在本文中，我们基于第一性原理计算，重点研究无序效应对LiMgPbSb 型Heusler 合金CoFe-TiSb 半金属性的影响，为后期的实验研究和器件开发提供理论指导.

2 计算方法

采用基于密度泛函理论(Density functional theory，DFT)的VASP(Vienna ab -initio Simulation Package)程序包，我们首先建立了包含16 个原子的四元Heusler 合金CoFeTiSb 的有序结构，并且进行了几何优化以找到其基态结构. 在几何优化后的CoFeTiSb 的有序结构中，我们互换一个Co原子和一个Fe 原子的位置从而形成浓度为25%的Co-Fe 交换无序，同理，我们互换一个Co 原子和一个Ti 原子的位置从而形成浓度为25%的Co-Ti 交换无序，互换一个Fe 原子和一个Ti 原子的位置从而形成浓度为25%的Fe -Ti 交换无序;并且对这三种交换无序结构分别进行几何优化. 在所有的计算中，我们采用Perdew-Burke -Ernzerhof(PBE)交换关联函数来处理核-电相互作 用;选 择 Co (3d74s2)、Fe (3d64s2)、Ti(3d24s2)、Sb(5s25p3)的价电子体系，7 ×7 ×7 的布里渊区k 点取样;1 ×10-6eV/原子的自洽场总能收敛标准和330eV 的能量截断;任意原子之间的相互作用力不超过0.03eV.

3 结果与讨论

我们首先讨论了处于有序结构的四元Heusler合金CoFeTiSb. 图2 为有序结构中，体系的总能量随晶格常数的变化曲线，我们可以看到，随着晶格常数从5.87Å 增加到6.07Å，体系的总能量逐渐下降;当晶格常数为6.07 Å 时，体系的总能量最低，处于基态稳定结构;而当晶格常数大于6.07Å 时，体系的总能量逐渐上升. 因此，有序结构的四元Heusler 合金CoFeTiSb 的平衡晶格常数为6.07 Å. 图3 给出了有序CoFeTiSb 在平衡晶格常数下的态密度以及Co 原子、Fe 原子和Ti 原子的d 轨道分波态密度. 有序CoFeTiSb 在费米面处具有一个明显的带隙，费米面恰好处于带隙的中部稍稍靠上的位置，因此，有序CoFeTiSb 具有稳定的半金属性. 此外，从分波态密度中我们可以清楚的看到，自旋向上未被占据的反键态和自旋向下被占据的成键态主要局域着Co 原子和Fe原子. 从表1 中可以得知，有序CoFeTiSb 的原胞总磁矩为2μB，非常的符合Slater -Pauling 规律，即原胞总磁矩=原胞总价电子数-24.

图2 CoFeTiSb 总能随晶格常数变化的关系. 箭头所指示的为基态时合金的晶格常数和总能Fig. 2 Total energy as function of lattice constant in CoFe-TiSb. The lowest energy and the corresponding lattice constant are indicated by an arrow

图3 CoFeTiSb 的总态密度和d 轨道分波态密度Fig. 3 Density of states (DOS)and d - partial density of states (d-PDOS)in CoFeTiSb

在有序结构的基础上，我们构建了三种不同无序结构，即Co -Fe、Co -Ti 和Fe -Ti 交换无序，它们的晶格常数以及晶胞总磁矩被列在表1中. Co-Fe 交换无序结构的晶格常数6.079 Å 最为接近有序结构，其晶胞总磁矩7.96μB也与有序结构非常接近;Fe -Ti 交换无序结构的晶格常数6.113 Å 与有序结构的晶格常数相差最大，并且其晶胞总磁矩9.14μB也与有序结构的的晶胞总磁矩之间的差距最大. 为了确定不同无序结构形成的可能性，我们计算了Co - Fe、Co - Ti 和Fe-Ti 交换无序结构的相对形成能. 交换无序结构的相对形成能(Ef)的计算公式为［20］:

表1 有序CoFeTiSb 合金以及Co -Fe、Co -Ti 、Fe -Ti交换无序结构的晶格常数、自旋极化率、晶胞总磁矩和相对形成能Table 1 The lattice constants，spin polarizations，total magnetic moments as well as relative formation energies of the ordered and Co -Fe，Co -Ti，Fe -Ti swap disordered structures

为了研究无序效应对CoFeTiSb 电子结构的影响，我们计算了CoFeTiSb 分别在Co-Fe、Co-Ti和Fe-Ti 交换无序下的总态密度图. 如图4 所示，阴影部分为有序CoFeTiSb 的总态密度图，我们可以看到在Co -Fe、Co -Ti 和Fe -Ti 交换无序中，自旋向上和自旋向下子能带均向高能区移动，并且自旋向下子能带带隙中均出现了一些极化峰，造成了CoFeTiSb 的半金属性的完全丧失.根据自旋极化率(P)计算公式:

其中，N↑代表自旋向上态密度，N↓代表自旋向下态密度. 在最难形成的Co - Ti 交换无序下，CoFeTiSb 的自旋极化率最低，仅为5%;在Fe -Ti 交换无序下，CoFeTiSb 的自旋极化率也下降到17%;而在最容易形成的Co - Fe 交换无序下，CoFeTiSb 的自旋极化率却高达85%. 这表明Co -Ti 和Fe -Ti 交换无序对CoFeTiSb 的自旋极化率的破坏最为严重，而Co -Fe 交换无序却对CoFe-TiSb 的自旋极化率影响较弱.

图4 Co -Fe、Co -Ti 和Fe -Ti 三种交换无序结构总态密度图Fig. 4 The DOSs of Co - Fe、Co - Ti and Fe - Ti swap disordered structures

4 总 结

我们采用基于密度泛函理论的GGA +PBE 计算方法，研究了CoFeTiSb 的电子结构，并且考虑了Co -Fe、Co -Ti 和Fe -Ti 交换无序对CoFe-TiSb 的电子结构的影响. 结果表明，有序CoFe-TiSb 是一种半金属材料，在费米面处具有100%的自旋极化率，其平衡晶格常数为6.07 Å，原胞总磁矩为2μB，与Slater -Pauling 规律符合的很好.Co-Fe、Co-Ti 和Fe-Ti 交换无序均完全破坏了CoFeTiSb 的半金属性，其中Co-Ti 交换无序形成的几率最低，对CoFeTiSb 自旋极化率的影响最大;Fe-Ti 交换无序较难形成，对CoFeTiSb 自旋极化率也有很大的影响;Co -Fe 交换无序形成的几率最高，但CoFeTiSb 在Co -Fe 交换无序下仍然保留了较高的自旋极化率.

［1］ Ohno H. Making nonmagnetic semiconductors ferromagnetic［J］. Science，1998，281(5379):951.

［2］ Farshchi R，Ramsteiner M. Spin injection from Heusler alloys into semiconductors:A materials perspective［J］. J. Appl. Phys.，2013，113(19):191101.

［3］ Hashimoto M，Herfort J，Schonherr H P，et al. Epitaxial heusler alloy Co2FeSi/GaAs(001)hybrid structures［J］. Appl. Phys. Lett.，2005，87(10):102506.

［4］ Wu B，Yang X D，Gao Q X. Structure，magnetism and spin-polarization in heusler alloy Co2CrGa(100)surface［J］. J. At. Mol. Phys.，2013，30(3):511(in Chinese)［吴波，杨秀德，高钦翔. Heusler 合金Co2CrGa(100)的表面结构、磁性和自旋极化［J］. 原子与分子物理学报，2013，30(3):511］

［5］ Wu B，Feng Y，Gao Q X. Magnetism and half -metallicity of Hg2CuTi - type heusler alloy Ti2FeB:the first - principles study ［J］. J. At. Mol. Phys.，2013，30(4):649 (in Chinese)［吴波，冯雨，高钦翔. 第一性原理研究Hg2CuTi 型Heusler 合金Ti2FeB 的磁性和半金属性［J］. 原子与分子物理学报，2013，30(4):649］

［6］ Pan Z K，Yang X D，Gao Q X，et al. Magnetism and half - metallic stability of half - Heusler compound NiMn1-xNbxSb ［J］. J. At. Mol. Phys.，2012，29(2):360 (in Chinese)［潘正坤，杨秀德，高钦翔，等. Half-Heusler 合金NiMn1-xNbxSb 的磁性和半金属稳定性［J］. 原子与分子物理学报，2012，29(2):360］

［7］ de Groot R A，Mueller F M，van Engen P G，et al.New class of materials:half - metallic ferromagnets［J］. Phys. Rev. Lett.，1983，50(25):2024.

［8］ Picozzi S，Continenza A，Freeman A J. Co2MnX (X=Si，Ge，Sn)Heusler compounds:An ab initio study of their structural，electronic，and magnetic properties at zero and elevated pressure ［J］. Phys. Rev. B，2002，66(9):094421.

［9］ Feng Y，Wu B，Yuan H K，et al. Electronic structure and magnetic properties of Ga - doped Heusler alloy Co2FeSi ［J］. Appl. Mech. Mater.，2012，130:1430.

［10］ Feng L，Tang C C，Wang S J，et al. Half -metallic full- Heusler compound Ti2NiAl:A first - principles study ［J］. J. Alloys Compd.，2011，509 (17):5187.

［11］ Feng Y，Wu B，Yuan H，et al. Magnetism and halfmetallicity in bulk and (1 0 0)surface of Heusler alloy Ti2CoAl with Hg2CuTi-type structure［J］. J. Alloys Compd.，2013，557(0):202.

［12］ Chen Y，Wu B，Feng Y，et al. Half-metallicity and magnetism of the quaternary inverse full-Heusler alloy Ti2-xMxCoAl (M = Nb，V)from the first-principles calculations［J］. Eur. Phys. J. B，2014，87(1):24.

［13］ Klaer P，Balke B，Alijani V，et al. Element-specific magnetic moments and spin-resolved density of states in CoFeMnZ (Z = Al，Ga;Si，Ge)［J］. Phys. Rev.B，2011，84(14):144413.

［14］ Alijani V，Winterlik J，Fecher G H，et al. Quaternary half-metallic Heusler ferromagnets for spintronics applications［J］. Phys. Rev. B，2011，83(18):184428.

［15］ Gao G Y，Hu L，Yao K L，et al. Large half-metallic gaps in the quaternary Heusler alloys CoFeCrZ (Z =Al，Si，Ga，Ge):A first -principles study［J］. J.Alloys Compd.，2013，551(0):539.

［16］ Miura Y，Nagao K，Shirai M. Atomic disorder effects on half - metallicity of the full - Heusler alloys Co2-(Cr1-xFex)Al:A first -principles study［J］. Phys.Rev. B，2004，69(14):144413.

［17］ Kandpal H C，Ksenofontov V，Wojcik M，et al. Electronic structure，magnetism and disorder in the Heusler compound Co2TiSn［J］. J. Phys. D:Appl. Phys.，2007，40(6):1587.

［18］ Raphael M P，Ravel B，Huang Q，et al. Presence of antisite disorder and its characterization in the predicted half-metal Co2MnSi［J］. Phys. Rev. B，2002，66(10):104429.

［19］ Fang Q L，Zhang J M，Xu K W，et al. The effect of defects on the magnetic properties and spin polarization of Ti2FeAl Heusler alloy［J］. J. Magn. Magn. Mater.，2014，351:25.

［20］ Van de Walle C G，Neugebauer J. First - principles calculations for defects and impurities:Applications to III - nitrides ［J］. J. Appl. Phys.，2004，95(8):3851.