强激光场中H- 离子二维光电子动量谱的理论研究

孙长平，崔宝凤

(1. 临沂大学理学院和凝聚态物理研究所，临沂276000;2. 临沂大学实验管理中心，临沂276000)

1 引 言

强场物理是当今物理学研究的重要前沿领域［1，2］. 原子分子的阈上电离(above -threshold ionization，ATI)是强激光场与原子分子相互作用的最基本的过程之一，能够为新型粒子加速器［3，4］、阿秒物理［5，6］和测量原子结构［7，8］等领域提供急需的数据和理论支持. 对强激光场中原子分子阈上电离的研究不仅能够很好地理解激光的性质，而且对理解原子分子与强激光场的相互作用机制具有重要的意义. 最近几十年，人们对强激光场中负离子阈上光离解的动量谱和能量谱进行了广泛的研究［9］，其中对H-离子，人们在实验上［10-12］和理论上［13-18］做了大量的研究.

在理论上，目前主要有强场近似(the strong-field approximation，SFA )方法和数值求解含时薛定谔方程(the time - dependent Schrödinger equation，TDSE)方法. 数值求解TDSE 方法能够得出比较精确的结果，但是计算量很大，受计算机硬件和软件的限制很大. SFA 方法用Volkov 态处理连续态，忽略了原子核对电离电子的库仑场影响，对激光场中负离子剥离后的母核影响很小，因此SFA 能够很好地用于强激光场中负离子的阈上光离解的研究［17，18］. 近年来，人们对中性原子［19-22］和负离子［18］二维光电子动量谱中最外层后重散射环进行了理论研究，但对二维光电子动量谱中出现的次外层后重散射环的研究还未见报道. 最近的研究结果表明［18］，利用SFA 方法得到的强激光场中H-离子二维光电子动量谱与数值求解TDSE 得到的结果符合得很好. 为了更好地研究强激光场中H-离子二维光电子动量谱，本文中我们选用两个模型势，利用SFA 方法研究了H-离子在不同强度的激光场中二维光电子动量谱中次外层后重散射环及模型势中的静电势和极化势对二维光电子动量谱的影响. 除特别标注外，本文均采用原子单位(a. u.).

2 理论方法

强激光场中动量为P 的H-离子的电离振幅表示为［23］:

第1 项和第2 项被称为SFA 的一阶振幅和SFA 的二阶振幅，分别表示为:

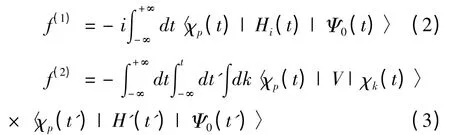
其中，V、Ψ0(t)和χp(t)分别为H-离子的模型势、初态波函数和动量为p 的光电子的Volkov 态波函数.

在线性极化激光场中，二维光电子动量谱定义为:

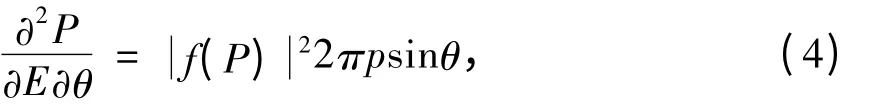
通过积分θ 角可以得能量谱:

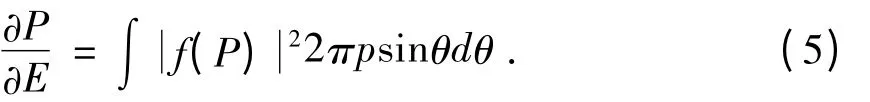
H-离子的初始波函数［24］可表示为:

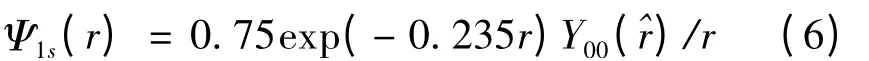
选用的两个模型势V1(r)［25］和V2(r)［24］分别为:

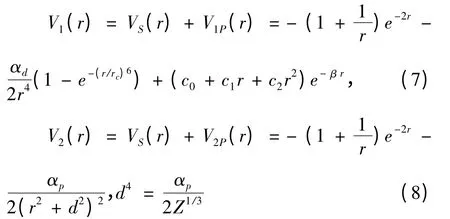
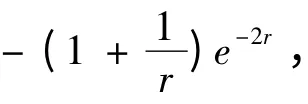
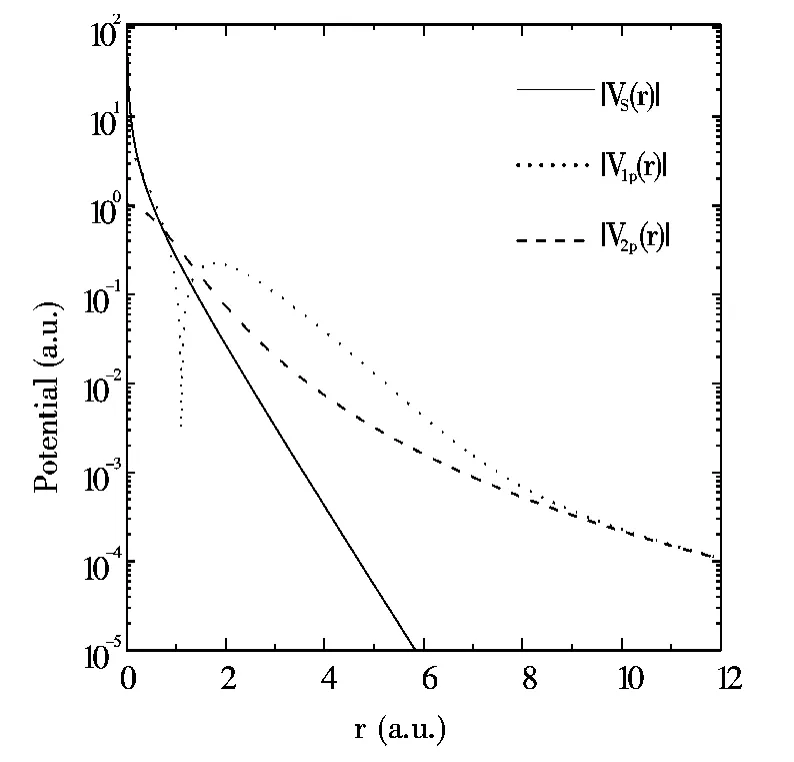
图1 H -离子的模型势V1(r)和V2(r)中静电势和极化势的示意图Fig.1 Schematic of the static potential and polarization potential in the model potentials V1(r)and V2(r)of H - ion

3 计算结果和讨论

计算中选用的沿z 轴方向的线性极化激光场的电场分量为:

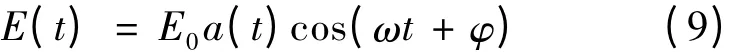
其中a(t)= cos2(πt/τ)为包络函数，ω 为激光的角频率，E0为电场的振幅，φ 为载波相位(φ =0)，激光脉冲取三个周期τ = 3T(≤τ/2).

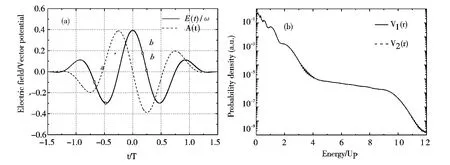
图2 (a)激光电场E(t)和矢势A(t)的示意图;(b)选用模型势V1(r)和V2(r)计算的能量谱的比较. 激光参数:λ =10600 nm，I=1.0 ×1011 W/cm2，τ =3TFig.2 (a)Schematic of the laser electric E(t)and the vector potential A(t)of a three - cycle laser pulse，with λ= 10600 nm and I= 1.0 ×1011 W/cm2. (b)Comparison of energy spectra of model potentials V1(r)and V2(r)

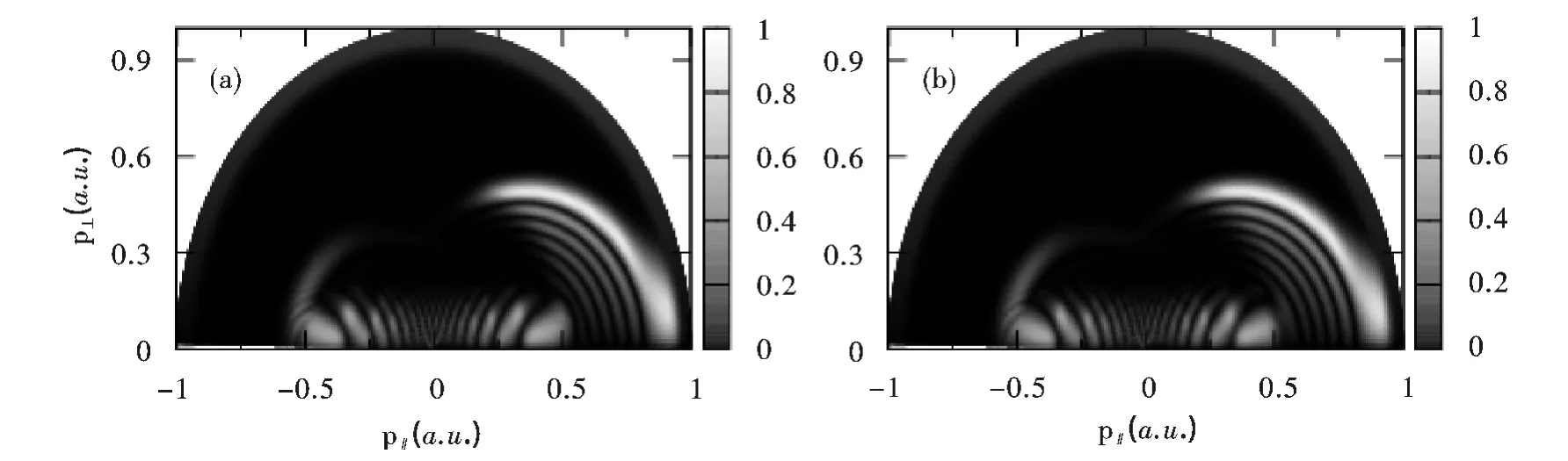
图3 选用模型势V1(r)和V2(r)计算的二维光电子动量谱. (a)模型势V1(r)的结果;(b)模型势V2(r)的结果. 激光参数同图2Fig.3 2D photoelectron momentum spectra calculated with (a)model positional and (b)model positional. (a)The result of model positional V1(r);(b)The result of model positional V2(r). The laser paramerers are the same as Fig.2

为了研究强激光场中H-离子光电子的二维动量谱中出现的次外层后重散射环及模型势中静电势和极化势对光电子的动量谱的影响，我们选用两个模型势V1(r)和V2(r)，利用上述SFA 方法分别计算了H-离子阈上光离解的能量谱和二维光电子动量谱. 激光场的电场E(t) = -∂A(t)/∂t 和矢势A(t)的示意图如图2 (a)所示. 选取的激光波长λ =10600 nm，激光强度I =1.0 ×1011W/cm2. 图2 (b)给出了选用模型势V1(r)和V2(r)计算的能量谱的比较，从图2 (b)中可以看出它们符合得很好. 由于模型势V1(r)和V2(r)仅有极化势不同(见图1)，因此两个模型势中的极化势对图2 (b)给出的能量谱影响很小.

图3 给出了选用模型势V1(r)和V2(r)计算的二维光电子动量谱. 由于光电子的能量在大于2 Up的几率密度很小(见图2 (b))，为了能够在同一个二维光电子动量谱中显示所有光电子的动量分布，图3 归一了二维光电子动量谱，使得出射的光电子在每个能量下具有相同的总产额. 图3中的横坐标p∥和纵坐标p⊥分别是光电子动量平行于激光极化方向和垂直于激光极化方向的分量.从图3 中可以看出，选用模型势V1(r)和V2(r)计算的二维光电子动量谱也符合得很好，因此两个模型势中的极化势对光电子的动量谱的影响也很小. 图3 中的右侧出现了多个半圆环，它们被称为后重散射环 (back rescattered ridges，BRR)［19］，本文中二维光电子动量谱右侧的BRR从右到左依次被标记为最外层BRR，次外层BRR、第三外层 BRR 等. 最近研究结果表明［18-22］，对于图3 中的二维光电子动量谱中右侧的最外层BRR 形成的原因能够从图2 (a)所示的激光场的电场E(t)和矢势A(t)示意图中得到很好地解释，即最外层BRR 形成的原因是图2(a)中“a”时刻附近H-离子电离的电子向右运动，然后在“b”时刻附近返回与靶原子(H 原子)发生重散射，向后重散射方向的电子形成了二维光电子动量谱中右侧的最外层的BRR. 光电子的动量由p = Ar+ pr或p∥= - Ar- prcosθr和p⊥= prsinθr给出，其中Ar是“b”时刻的矢势，pr是BRR 的半径，Ar与pr关系满足经典计算得到的关系式pr= 1.26Ar，θr是后散射角，90o≤θr≤180o. 为了更好地研究BRR 的形成原因，我们研究了分别沿着图3 (a)和图3 (b)中次外层BRR 光电子的角分布，其中圆心Ar=0.351，半径pr=0.439，这与利用经典理论关系式pr=1.26Ar得到的pr= 0.442 相符合，误差仅为0.68%. 图4 (a)和图4 (b)分别给出了沿着图3 (a)和图3 (b)中次外层BRR 光电子的角分布及多项式拟合的结果与利用第一波恩近似(the first Born approximation，FBA)计算的微分弹性散射界面的比较. 从图4 (a)和图4 (b)中可以看出选用模型势V1(r)和V2(r)计算的结果符合得很好，虽然沿着次外层的光电子角分布具有很小的波动性，但多项式拟合的结果与利用FBA 计算的结果符合得很好. 图3 中的二维光电子动量谱中次外层BRR 出现的原因与最外层BRR 形成原因的研究结果［18-22］相似，也能够从图2 (a)所示的激光场的电场E(t)和矢势A(t)示意图中得到很好地解释，即次外层BRR 形成的原因为图2(a)中“a’”时刻附近H-离子电离的电子向右运动，然后在“b’”时刻附近返回与靶原子(H原子)发生重散射，向后重散射方向的电子形成了次外层的BRR.

为了研究不同强度的波长为10600 nm 激光场中H-离子二维光电子动量谱，选用上述的模型势V1(r)和V2(r)，研究了H-离子在强度分别为5.0 ×1010W/cm2，2.0 ×1011W/cm2和3.0 ×1011W/cm2的激光场中的二维光电子动量谱. 图5 给出了计算结果，左列和右列分别是选用模型势V1(r)和V2(r)计算的结果，从上到下激光强度为5 ×1010W/cm2，2.0 ×1011W/cm2和3.0 ×1011W/cm2. 从图5 中可以看出，两个模型势计算的结果符合得很好，随着激光强度的增加，二维光电子动量谱中出现更多的BRR. 为了定量的研究沿着图5 (a) - (f)中出现的次外层BRR，图6 (a) - (f)分别给出了沿着图5 (a) - (f)次外层BRR 光电子的角分布及多项式拟合的结果与利用FBA 计算的微分弹性散射界面的比较. 图6 (a) - (f)表明:模型势V1(r)和V2(r)中的极化势对二维光电子动量谱的影响很小;随着激光强度的增强，沿着次外层BRR 光电子的角分布出现波动性变小，通过多项式拟合次外层光电子角分布得到的结果与利用FBA 计算的结果符合得很好，因此可以通过多项式拟合BRR 光电子的角分布的方法获得电子与母核的弹性散射截面，特别适用于激光强度较小的情况. 图6 (a) - (f)二维光电子动量谱中出现BRR 数目和沿着次外层BRR 的光电子的角分布波动性变化的原因是由H-离子在不同强度激光场中电离的光电子与母核发生重散射的几率不同引起的. 为了进一步检验我们的计算结果，表1 给出了图6 中次外层BRR以Ar为圆心“测量”的半径pr与利用经典理论计算的pr的比较. 从表1 可以看出从次外层BRR“测量”的半径pr与利用关系式pr= 1.26Ar计算的pr符合得很好，激光强度的越大误差越小，最大误差来自于激光强度为5.0 ×1010W/cm2的pr，约为1.36%.

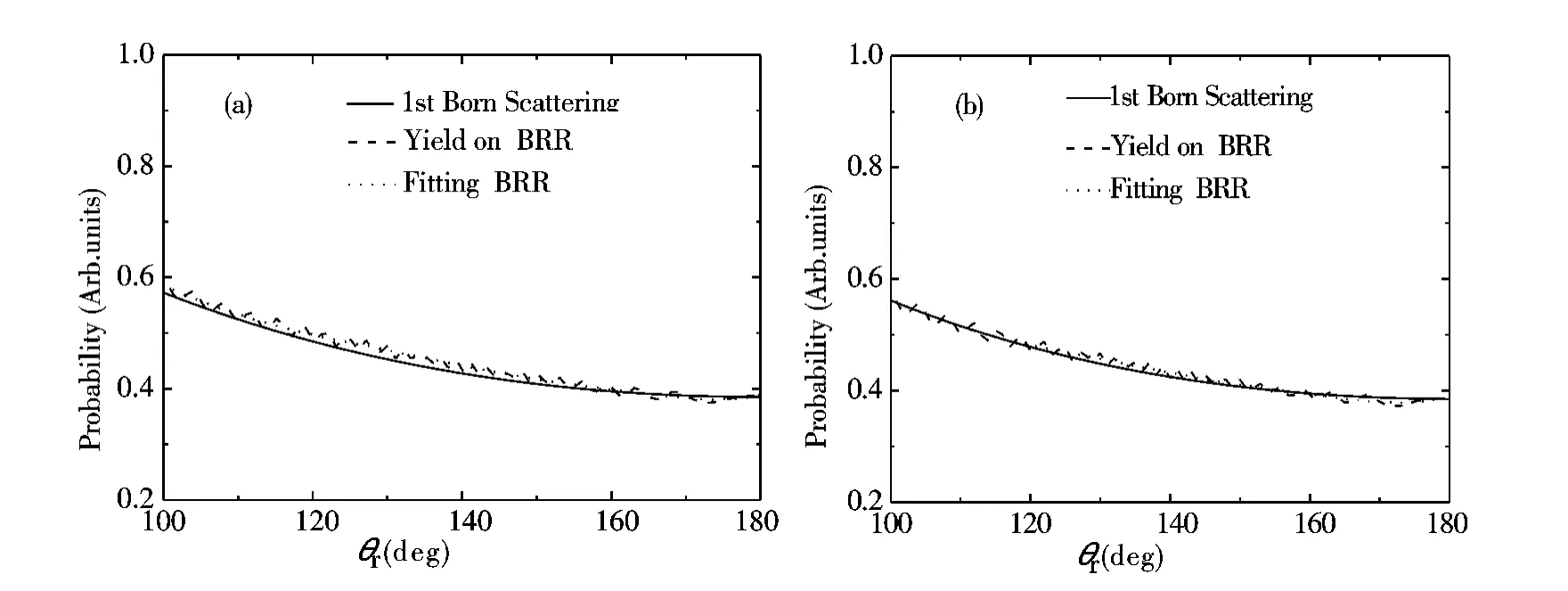
图4 H -离子沿着次外层BRR 光电子的角分布及多项式拟合的结果与利用FBA 计算的微分弹性散射界面的比较. 图4 (a)和图4 (b)分别是沿着图3 (a)和图3 (b)次外层BRR 得到的光电子的角分布Fig.4 Angular distributions of photoelectrons along the second outermost BRR and the polynomial fitting results of them for H - compared to the differential elastic scattering cross sections calculated using the FBA. Fig. 4 (a)and Fig.4 (b)are the second outermost BRR along the Fig. 3 (a)and Fig.3 (b)，respectively

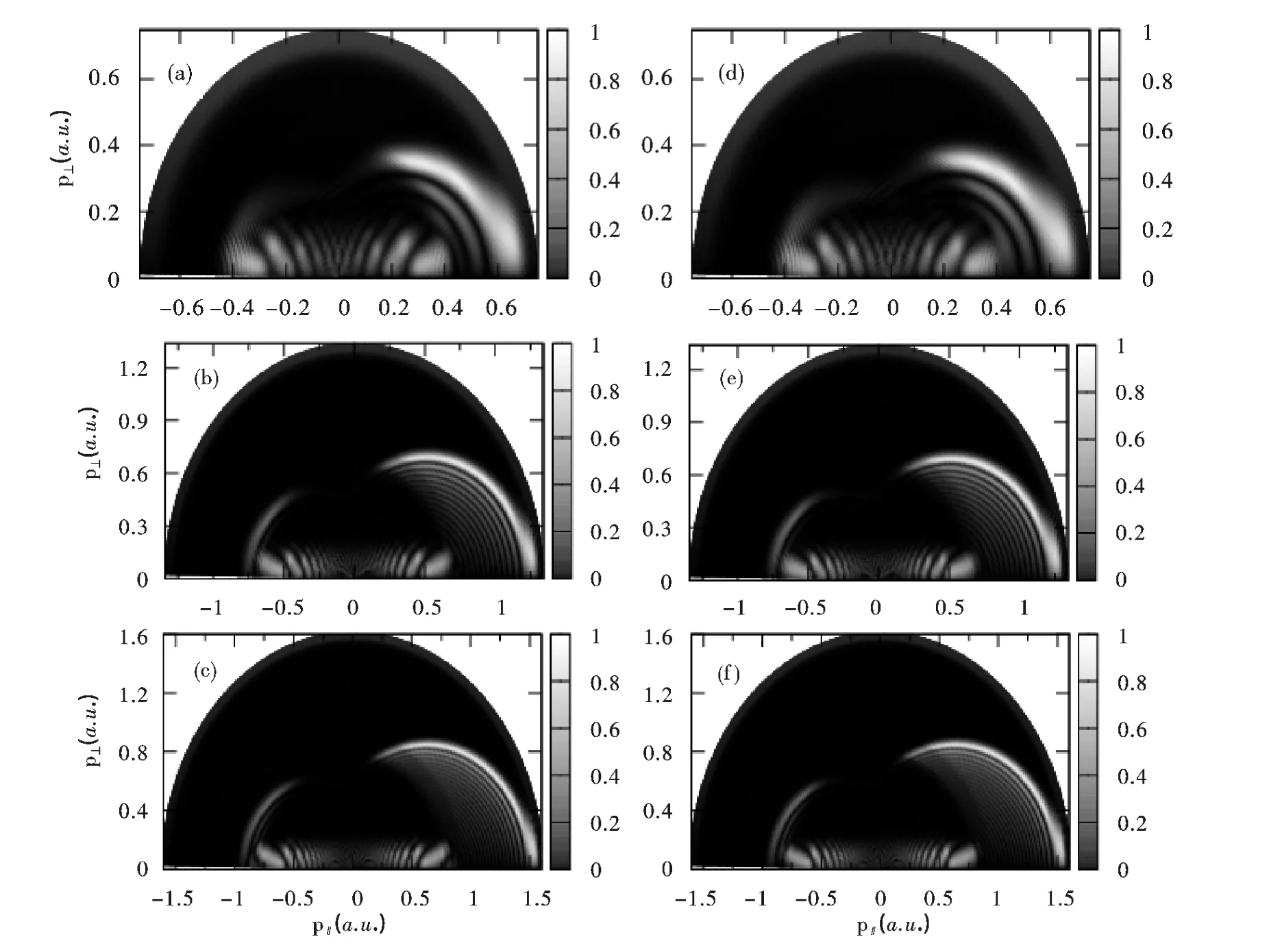
图5 H -离子在不同激光强度中二维光电子动量谱. 左列和右列分别为选用模型势V1(r)和V2(r)计算的结果. 从上到下激光强度为5 ×1010 W/cm2，2.0 ×1011 W/cm2 和3.0 ×1011 W/cm2Fig.5 2D photoelectron momentum spectra of H - ion in the different laser intensities. Left column and right column are the calculation results of model potentials V1(r)and V2(r)，respectively. From up to down，the laser intensities are，respectively，0.5 ×1011，2.0 ×1011，and 3.0 ×1011 W/cm2

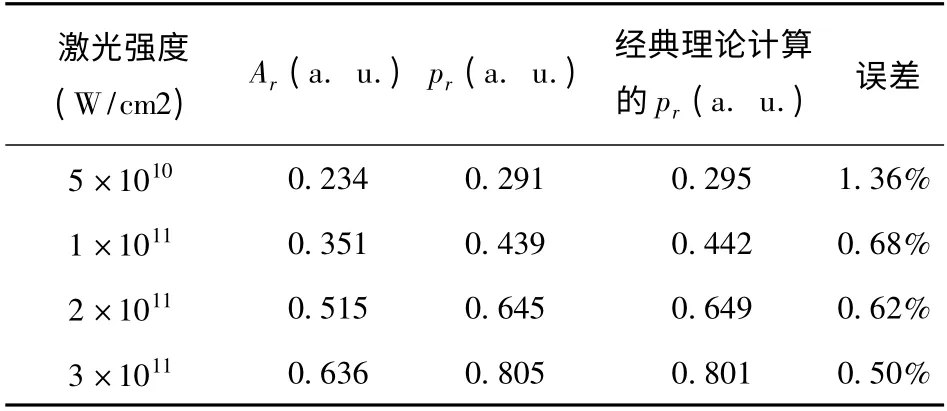
表1 图6 中次外层BRR 以Ar 圆心“测量”的半径pr 与经典理论计算的pr 的比较Table 1 Comparison of the“measured”radius pr as the circle center Ar in the second outmost BRR of Fig.6 with the pr calculated by the classical theory

图6 选用模型势V1(r)和V2(r)计算的沿着次外层BRR 的光电子的角分布及多项式拟合的结果与使用FBA 计算的微分弹性散射界面的比较. 左列和右列分别为模型势V1(r)和V2(r)的结果，图6 (a)- (c)和图6 (d) - (f)分别为沿着图5 (a) -5 (c)和沿着图5 (d)- (f)次外层BRR 的光电子的角分布Fig.6 Angular distributions of photoelectrons along the second outermost BRR and the polynomial fitting results of them calculated using model potential V1(r)and V2(r)were compared to the differential elastic scattering cross sections calculated using the FBA. Left section and right section are the results of model potentials V1(r)and V2(r)，respectively. Fig. 6 (a)-(c)and Fig. 6 (e)- (f)are the second outermost BRR along the Fig. 5 (a)- (c)and Fig. 5 (d)- (f)，respectively

4 结 论

选用两模型势V1(r)和V2(r)，利用SFA 方法研究了H-离子在不同强度的激光场中二维光电子动量谱中次外层BRR. 研究结果表明:两个模型势中的极化势对二维光电子动量谱的影响很小;随着激光强度的增强，二维光电子动量谱中BRR 的数目增多，沿着次外层BRR 光电子的角分布波动性变小. 虽然沿着次外层BRR 光电子的角分布具有波动性，但是可以通过多项式拟合BRR 光电子的角分布的方法获得精确的电子与母核的弹性散射截面，特别适用于激光强度较小的情况. 虽然SFA 方法与数值求解TDSE 方法相比，忽略了母核对电离电子的库仑场影响和原子激发态的贡献，但是由于H-离子与光离解的电子没有库仑作用，因此从理论上来讲SFA 方法是一种研究负离子在强激光场中的光离解的有效的方法，具有计算量小、计算精度高、物理过程清晰等优点. 本文的研究结果对于研究负离子体系在强激光场中的阈上光离解具有一定的参考价值.

［1］ Zhang J. High field physics-a new scientific arena［J］.Phys.，1997，26:643 (in Chinese)［张杰. 强场物理—一门崭新的学科［J］. 物理，1997，26:643］

［2］ Brabec Th，Krausz F. Intense few-cycle laser fields:Frontiers of nonlinear optics［J］. Rev. Mod. Phys.，2000，72:545.

［3］ Moore C I，Ting A，McNaught S J，et al. A laser-accelerator injector based on laser ionization and pondermotive acceleration of electrons［J］. Phys.Rev.Lett.，1999，82:1688.

［4］ Salamin Y I，Faisal F H M. Ultrahigh electron acceleration and Compton emission spectra in the superintense laser pulse and a uniform axial magnetic field ［J］.Phys.Rev.A，2000，61:043801.

［5］ Baltuška A，Udem Th，Uiberacker M，et al. Attosecond control of electronic processes by intense light fields［J］. Nature，2003，421:611.

［6］ Sansone G，Benedetti E，Calegari F，et al. Isolated single-cycle attosecond pulses ［J］. Science，2006，314:443.

［7］ Hentschel M，Kienberger R，Spielmann Ch，et al. Attosecond metrology［J］. Nature，2001，414:509.

［8］ Kienberger R，Goulielmakis E，Uiberacker M，et al.Atomic transient recorder ［J］. Nature，2003，427:817.

［9］ Krausz F，Ivanov M. Attosecond physics［J］. Rev.Mod. Phys.，2009，81:163.

［10］ Præstegaard L，Andersen T，Balling P. Two-photon detachment of H2in the vicinity of the one-photon detachment threshold ［J］. Phys. Rev. A，1999，59:R3154.

［11］ Reichle R，Helm H，Kiyan I Y. Photodetachment of H-in a strong infrared laser field ［J］. Phys. Rev.Lett.，2001，87:243001.

［12］ Zhao X M，Gulley M S，Bryant H C，et al. Nonresonant excess photon detachment of negative hydrogen ions［J］. Phys. Rev.Lett.，1997，78:1656.

［13］ Arendt C，Dimitrovski D，Brigg J S. Electron detachment from negative ions by few-cycle laser pulses:Dependence on pulse duration ［J］. Phys. Rev. A，2007，76:023423.

［14］ Telnov D A，Chu Shih-I. Above-threshold multiphoton detachment from the H-ion by 10.6 μm radiation:Angular distributions and partial width ［J］. Phys.Rev. A，1994，50:4099.

［15］ Frolov M V，Manakov N L，Pronin E A，et al. Modelindependent quantum approach for intense laser detachment of a weakly bound electron［J］. Phys. Rev.Lett.，2003，91:053003.

［16］ Krajewska K，Fabrikant I I，Starace A F. Threshold effects in strong-field detachment of H-and F-:Plateau enhancements and angular distribution variations［J］. Phys. Rev. A，2006，74:053407.

［17］ Bauer D，Milosevic D B，Becker W. Strong-field approximation for intense-laser-atom processes: the choice of gauge ［J］. Phys. Rev. A，2005，72:023415.

［18］ Zhou X X，Chen Z，Morishita T，et al. Retrieval of electron-atom scattering cross sections from laser-induced electron rescattering of atomic negative ions in intense laser fields［J］. Phys. Rev. A，2008，77:053410.

［19］ Chen Z，Morishita T，Le A-T，et al. Analysis of twodimensional high-energy photoelectron momentum distributions in the single ionization of atoms by intense laser pulses［J］. Phys. Rev. A，2007，76:043402.

［20］ Morishita T，Le A T，Chen Z，et al. Accurate retrieval of structural information from laser-induced photoelectron and high-order harmonic spectra by few-cycle laser pulses ［J］. Phys. Rev. Lett.，2008，100:013903.

［21］ Chen Z，Le A T，Morishita T，et al. Origin of species dependence of high-energy plateau photoelectron spectra［J］. J. Phys.B，2009，42:061001.

［22］ Sun C P，Zhao S F，Chen J H，et al. Two-dimensional photoelectron momentum distributions of hydrogen in intense laser field［J］. Chin. Phys. B，2011，20:113201.

［23］ Becker W，Grasbon F，Kopold R，et al. Progress in ultrafast intense laser science ［J］. Adv. At. Mol.Opt. Phys.，2002，48:35.

［24］ Gazibegovi c'-Busuladži c' A，Miloševi c' D B，Becker W. High-energy above-threshold detachment from negative ions ［J］. Phys. Rev. A，2004，70:053403.

［25］ Laughlin C，Chu Shih-I. Multiphoton detachment of H-［J］. Phys. Rev. A，1993，48:4654.