基于图正则化与非负组稀疏的自动图像标注

钱智明 钟 平王润生

(国防科技大学电子科学与工程学院 长沙 410073)

基于图正则化与非负组稀疏的自动图像标注

钱智明 钟 平*王润生

(国防科技大学电子科学与工程学院 长沙 410073)

设计一个稳健的自动图像标注系统的重要环节是提取能够有效描述图像语义的视觉特征。由于颜色、纹理和形状等异构视觉特征在表示特定图像语义时所起作用的重要程度不同且同一类特征之间具有一定的相关性，该文提出了一种图正则化约束下的非负组稀疏(Graph Regularized Non-negative Group Sparsity, GRNGS)模型来实现图像标注，并通过一种非负矩阵分解方法来计算其模型参数。该模型结合了图正则化与l2,1-范数约束，使得标注过程中所选的组群特征能体现一定的视觉相似性和语义相关性。在Corel5K和ESP Game等图像数据集上的实验结果表明：相较于一些最新的图像标注模型，GRNGS模型的鲁棒性更强，标注结果更精确。

图像标注；图正则化；组稀疏；非负矩阵分解

1 引言

随着图像获取与存储技术的不断进步，图像数据呈现井喷式增长。如何检索这些图像是当前计算机视觉领域的一大难题。一般而言，用户倾向于用文本查找相关图像，这使得自动图像标注技术受到了研究者们的广泛关注。然而，由于“语义鸿沟”的存在，自动图 像标注是一件极具挑战性的任务。这里的“语义鸿沟”主要体现在很难建立低层视觉特征与高层图像语义之间的相互映射关系。由于高层语义所对应视觉内容往往非常复杂，这里主要从多类特征选择和人的认知需求两个方面来分析视觉特征对语义理解的影响。

由于图像内容千变万化，仅仅使用一类视觉特征往往不足以满足不同图像语义的需求，所以图像通常由多类异构视觉特征所共同表示。然而，这种高维的混合图像特征在表示图像特定语义时往往是冗余的。因此，选择一个合理而又紧凑的图像表示方法将能够大大地提高图像标注的效率。在处理高维特征方面，稀疏表示被证明是极其有效的[1]。对于图像标注而言，稀疏表示的意义主要体现在：尽管丰富的图像内容需要由高维特征来表示，但属于某一特定语义类别的图像往往可以由若干低维空间的视觉特征来很好地描述。近年来，有很多图像标注方法[2,3]都通过对特征系数施以l1-范数约束来兼顾模型误差与特征系数的稀疏性，以获取更加稳健和准确的标注结果。但是，这些方法仅考虑了各独立特征对图像标注的不同作用，而忽略了特征之间的相关性对标注结果的影响。一般情况下，同类特征之间往往相关性较大，而异类特征对某一图像语义则往往表现出不同的描述能力。例如，纹理特征能够很好地用于指纹识别，而形状特征则对车辆检测有着较好的效果。这也就是说，选择合适的组群特征能够更加有效地描述图像语义。为此，组稀疏方法[4−8]结合了传统稀疏表示的l1-范数约束与岭回归中的l2-范数约束，使得在针对某一图像语义的特征组选择上尽可能保持稀疏，而在用同类特征表示图像时则使损失误差尽可能小。例如，Wu等人[5]构建了一个结构化的稀疏选择模型来应对图像标注过程中的特征组选择问题。Yang等人[6]则在此基础上提出了一种拉普拉斯联合组稀疏模型(Laplacian Joint Group Lasso, LJGL)，用于从训练数据中重构图像区域，并根据区域特性来赋予标注信息。考虑到图像数据中的多层特征结构，Gao等人[7]提出了一种多层组稀疏编码的方法来实现图像分类与标注。最近，Jayaraman等人[8]将结构化组稀疏用于多任务学习，以此选择判别性较强的特征类，从而保持具有一致性的特征间的相关性并降低非相关特征对结果的影响。Bahrampour等人[9]则将树结构组稀疏方法用于多模分类，如多视角人脸识别，多传感器目标分类等。此外，组稀疏方法在视频[10]、文档[11]以及网页数据分析[12]上也有着极具前景的应用。这些方法表明组稀疏模型能够提取最具相关性的低层特征组来对高层语义进行建模，大大提高了模型的学习效率与应用性能。

在人的认知需求方面，一些心理学和生理学上的证据表明：基于部件(part-based)的表示方法在一定程度上能够很好地描述人类大脑的认知模式[13,14]。这里的部件可以指图像的局部结构或目标的组成部分，也可以指视觉特征的部分属性。这一结论为进一步描述图像语义提供了有力理论支撑。非负矩阵分解(Non-negative Matrix Factorization, NMF)[13]就是一种典型的用于学习目标部件的方法。由于NMF在求解过程中只包含加性的而不含减性的矩阵运算，这与目标部件表示的过程相吻合，所以其结果能够在一定程度上较好地表示目标部件。然而，NMF在处理数据时假设数据的分布是全局线性的，而没有考虑数据的内蕴几何结构，这就使得NMF在处理具有非线性流形结构的数据时其效果往往不尽人意。于是，一些研究工作开始关注流形子空间里的数据处理问题。其中，图正则化[6,14]是研究数据流形结构的最重要的方法之一。这类方法一般假设：如果数据点在原空间是邻近点，那么对应到新的基下也是邻近点。根据这一假设，图正则化与传统的线性降维方法相比，能够更好地保持数据的内在几何结构。

本文提出了一种图正则化约束下的非负组稀疏(Graph Regularized Non-negative Group Sparsity, GRNGS)模型来实现图像标注。相较于以往的组稀疏模型，GRNGS模型考虑到了图像视觉特征空间的流形结构和非负特征对图像理解所起到的作用，并根据这些特性选择符合人眼视觉且最具鉴别力的图像特征，以实现更高效的图像标注。同时，利用特征的非负性，该模型参数可通过非负矩阵分解来有效地求解。

2 本文方法

如图1所示，整个标注框架由模型构建与模型测试两部分组成。在模型构建过程中，我们根据多种异构视觉特征和图像语义信息来训练模型参数；在模型测试过程中，我们首先提取测试图像的多种异构视觉特征，然后根据模型参数计算各语义标签的后验概率，并对所求概率进行排序以确定标注结果。

2.1 组稀疏模型

给定一图像训练集{(xi,yi)∈ℝp×{0,1}C, i=1,2,…,n}，其中xi=[xi1xi2…xip]T∈ℝp表示第i幅图像的特征向量，yi=[yi1yi2…yiC]T∈{0,1}C表示第i幅图像所对应的标注信息(即如果该图像的标注信息中有标签k，则yik=1；否则，yik=0)。图像特征一般由多种异构视觉特征所组成，这里我们假设p维图像特征中含有G组不同类别的特征。用mg表示第g组特征的维数，则有。于是，第i幅图像的特征向量可重新表示为xi=。令X=[x1x2…xn]T为n×p的训练特征矩阵，Y=[y1y2…yn]T为n×C的标注矩阵，则结合组稀疏方法的图像标注问题可表示为

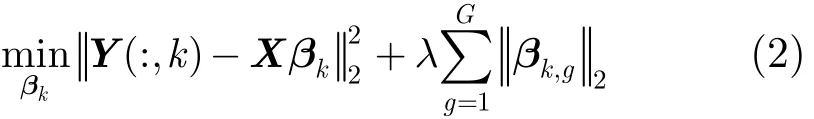
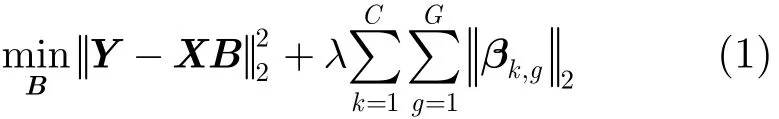
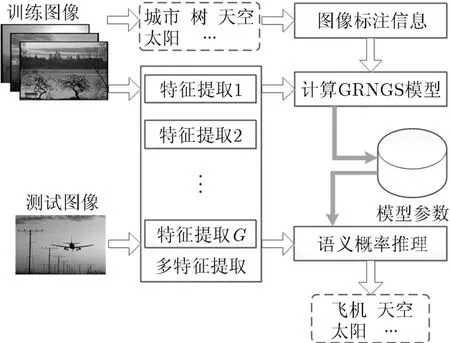
图1 基于GRNGS模型的图像标注框架

其中，λ＞0为组稀疏因子，B=[β1β2…βC], βk=[βk1βk2…βkp]T∈ℝp为标记标签k时的系数矢量，βk,g为第g组特征所对应的系数矢量。该方法可通过调节λ选择对标注问题有意义的特征组，即βk,g≠0，并根据这些特征组来建立图像视觉特征与图像语义间的映射关系。由于每一语义标签所对应的特征系数各不相同，我们将上述矩阵求解问题进一步细分为标签k所对应的矢量求解问题。

2.2 GRNGS模型

为了有效地利用图像特征的组效应、流形结构的紧凑性和非负性，本文提出了一种GRNGS模型来实现图像标注。流形是线性子空间的一种非线性推广，我们也可以将流形看作是一个局部可坐标化的拓扑空间。要保持上一节所描述的图像标注问题中流形结构的紧凑性，可根据图正则化方法中较典型的拉普拉斯特征映射(Laplacian Eigenmap, LE)[14]来寻找一个最佳映射，使得下面的损失函数最小：

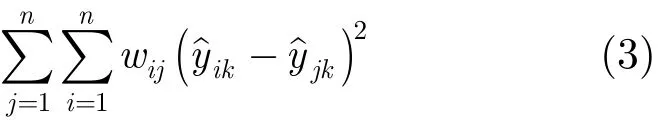
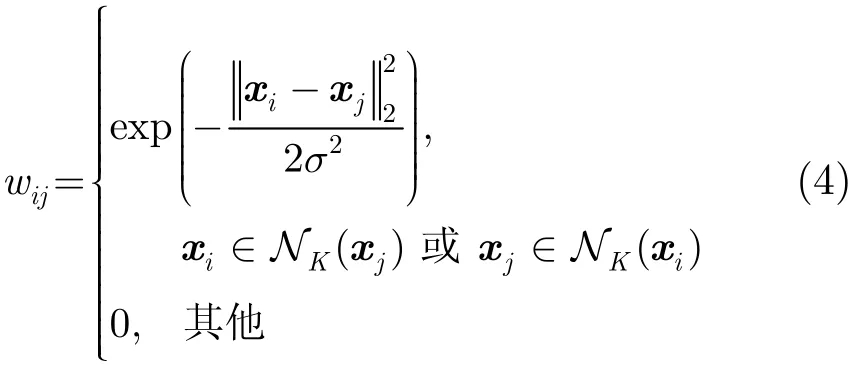
其中，σ为一带宽参数，NK(·)表示K近邻搜索函数。于是，引入模型参数的非负约束以及式(3)中的流形约束，我们可将式(2)中的标注问题改为

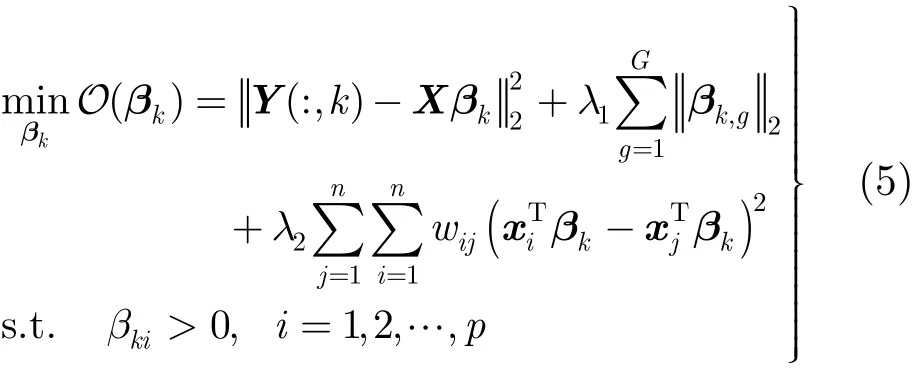
其中，λ1＞0为组稀疏参数，用以选择合适的特征组；λ2＞0为图正则化参数，用以控制模型结构的复杂度。

令

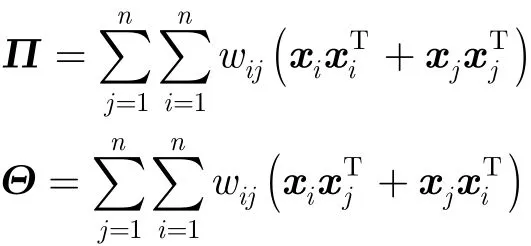
则式(5)可重写为

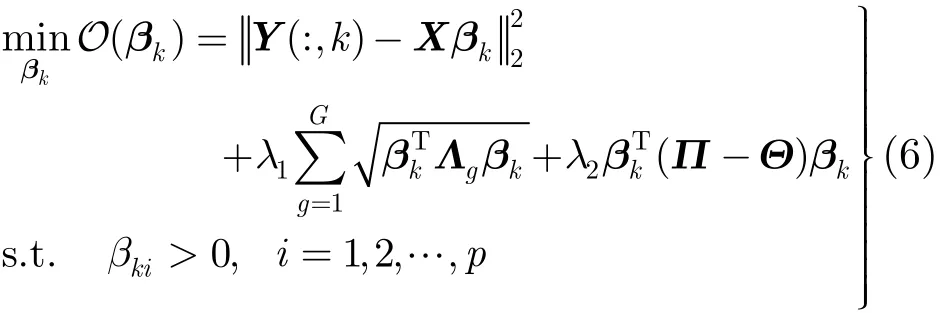
对于一幅测试图像xnew，根据式(6)中所求的βk获得标签k对该图像的后验概率：

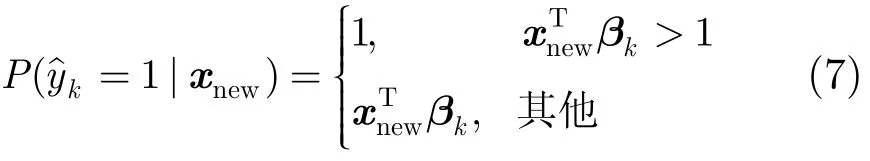
对所有标签的后验概率进行降序排序，则可取后验概率最大的若干标签对该图像进行标注。

2.3 模型优化

为了求解式(6)中的优化问题，本文提出一种非负矩阵分解算法。首先，我们定义拉格朗日函数：

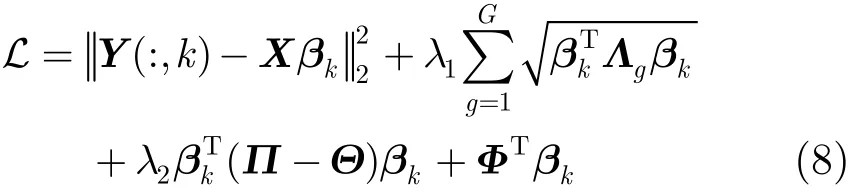
其中，Φ=[φ1φ2…φp]T为拉普拉斯乘子。对式(8)求导，可得φiβki=0)，并使∂L/∂βk=0，可得

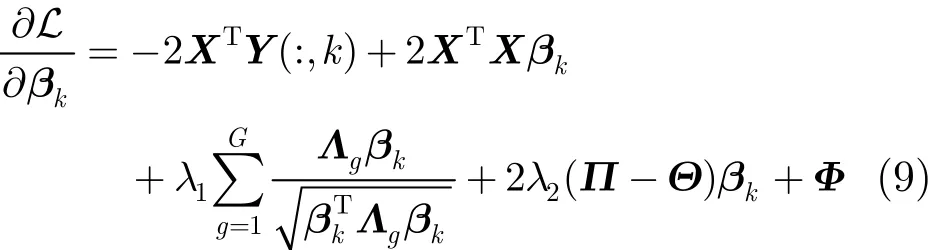
为了确保算法的收敛性，利用K.K.T.条件[14](即

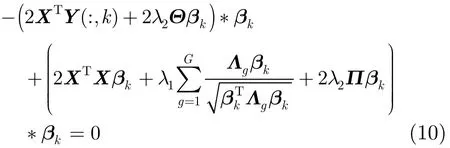
其中，“∗”表示Hadamard积[15]。于是，我们可得模型优化算法的非负迭代过程如下：

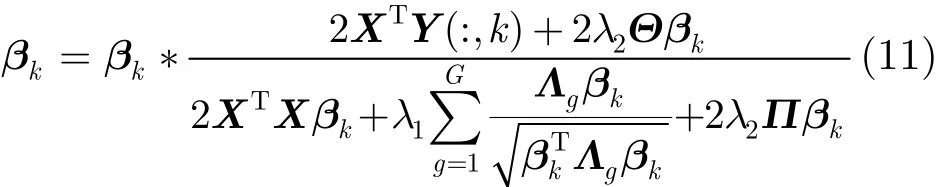
这里，矢量商a/b是指矢量a和b中各元素值的商。该优化算法的具体过程如下：

第1步 计算Π,Θ,Λg，令迭代次数t=0，初始化；

2.4 模型分析

由于Π,Θ在给定数据的情况下是固定的，其计算复杂度为O(n2p2)。在每次迭代过程中，分母项的计算复杂度为O(np+p2) ，分子项的计算复杂度为O(np2)，因而其每次迭代过程的计算复杂度为O(np2)，与图像个数是线性相关的，这对于大规模数据库的标注工作是极其有利的。另外，非负迭代过程的迭代次数与所求系数矢量的维数一般是成比例的，故总的计算复杂度为O(n2p2+np3C)。

3 实验

本文实验安排如下：首先，给出实验数据和评价准则等信息；然后，对实验参数进行了评估；最后，给出了GRNGS模型与其他模型在图像标注上的性能对比结果。

3.1 实验设置

本文采用的数据集包括：Corel5K数据集[16]和ESP Game数据集[17]，其详细信息如表1所示。

表 1 实验数据集详细信息

在特征提取方面，按照特征属性不同将特征分为不同组群。本文实验所采用的特征维数共320维，具体描述如下：128维的CPAM(Colored Pattern Appearance Model)特征[18]，96维的RGB和HSV颜色直方图特征(每个颜色通道提取16维特征)，32维的梯度和方向直方图特征，64维的形状特征[19]。对于每一特征，我们将其值转换到区间[0,1]上来，并对转换后的特征值进行归一化处理，即∀xi，有。

为了对标注结果进行合理评价，本文采用两种评价策略：第一，固定每幅图像的语义标签数为5，计算查准率(Prec@5)和查全率(Rec@5)[18]；第二，针对不同的查全率，计算所有平均查准率的平均值(Mean Average Precision, MAP)：

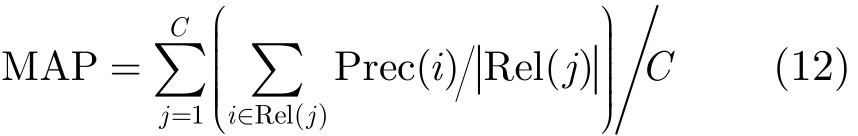
此外，所有实验均在Matlab 2010平台上运行，实验所用计算机的主频为2.30 GHz, RAM内存为8 G。

3.2 模型参数对图像标注的影响

GRNGS模型主要需考察3个参数：式(4)中的最近邻参数K，式(6)中的组稀疏参数λ1和图正则化参数λ2。由于最近邻参数K与另外两个参数的相关性较弱，我们将分开对其进行评估，并使用MAP来衡量各参数取值的实验结果。首先，我们令K=100，并考察参数λ1和λ2。在本实验中，我们对这两参数分别取值{0.0001,0.001,0.01,0.1,1,10}。

图2给出了GRNGS模型在不同参数设置下的标注结果。我们发现当λ1=λ2时，标注结果相对较好。在接下来的实验中，我们选取标注结果最好的模型参数作为实验参数，即在处理Corel5K和ESP Game数据集时分别选取参数λ1=λ2=0.1和λ1= λ2=0.01。

接下来，我们考察最近邻参数K对实验结果的影响。由图3可知，在K值较小时，标注结果随着K值的增加而逐步改善；而当K达到一定值时，标注结果的MAP值则相对稳定或略微呈下降趋势。据此，我们在接下来的所有实验中均令K=200。

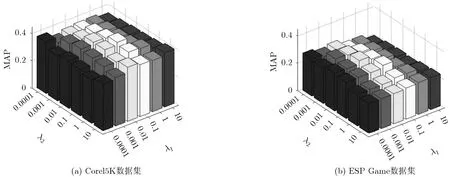
图2 GRNGS模型在不同组稀疏参数和图正则化参数下的标注结果比较

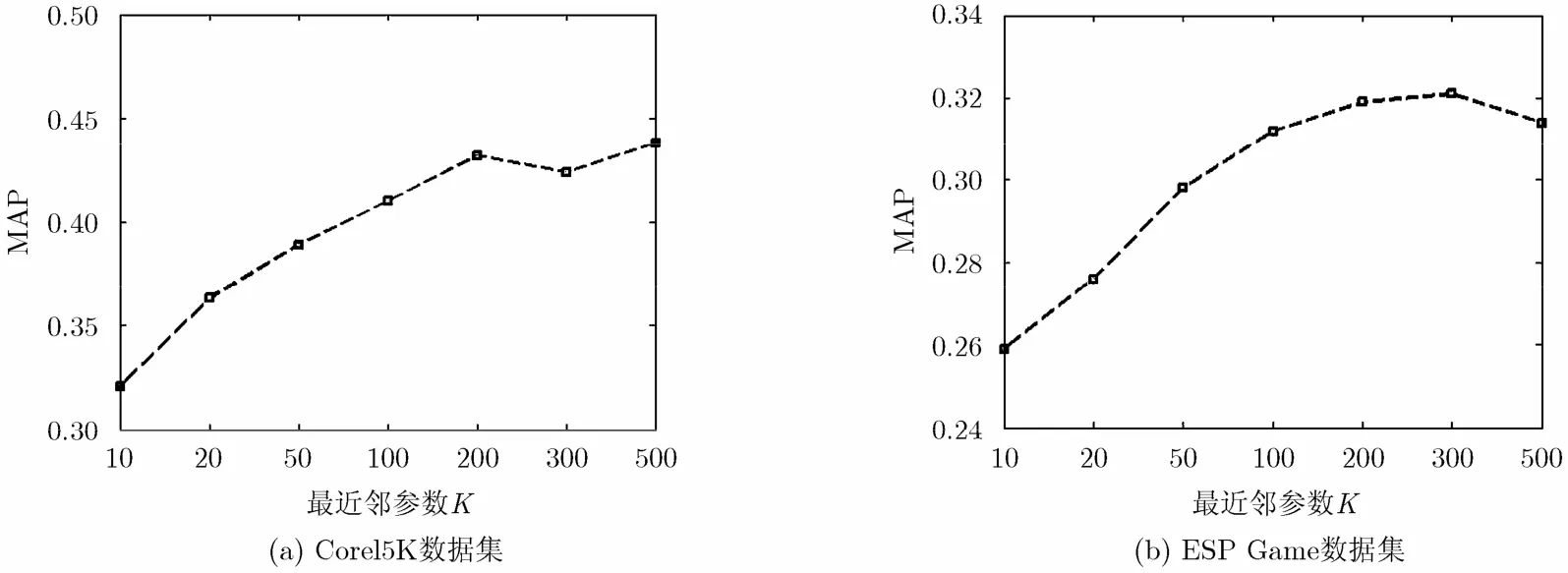
图3 GRNGS模型在不同最近邻参数下的标注结果比较

3.3 算法收敛性分析

为了验证本文所提的非负矩阵分解算法的收敛性，我们对两个数据库的建模过程进行了跟踪，并通过计算式(6)中的目标函数值来确定其收敛状态。如图4所示，GRNGS模型的优化算法在两个数据集上都是收敛的。具体来讲，该算法在Corel5K数据集上仅需不到50次迭代就可达到收敛条件；而在ESP Game数据集上达到收敛的迭代次数则需600次左右。另外，仅考虑算法的收敛过程，本文针对GRNGS模型所提的优化算法在Corel5K和ESP Game数据集上的用时分别为5 min 29 s和12 min 45 s。这些实验结果均反映了本文所提的模型优化算法具有较好的收敛性能，且计算复杂度较低，有利于算法的进一步推广和应用。

3.4 模型参数结构比较

为了更好地分析GRNGS模型的模型参数，我们将该参数与NMF和图正则化的非负矩阵分解(Graph-regularized Nonnegative Matrix Factorization, GNMF )[14]所得的模型参数进行稀疏性和结构比较。图5显示了这3种方法在Corel5K数据集和ESP Game数据集上所学习得到的模型参数。这3种模型在Corel5K和ESP Game数据集上的参数矩阵分别为320×374和320×268。从这些结果可以看出，GNMF的稀疏性一般比GRNGS和NMF差，而GRNGS在较大的ESP GAME数据集上的稀疏性明显强于NMF和GNMF。同时，GRNGS所学习得到的矢量具有明显的组效应和较好的一致性，从而体现了组群特征的相关性且能够去除不相关特征的干扰，以更好地满足图像部分属性特征表示的需求。

3.5 图像标注结果比较与分析

为了更好地分析GRNGS模型在图像标注方面的性能，本文所比较的方法包括一些基准图像标注方法和与本文方法最为接近的若干方法。基准图像标注方法包括：SVM模型和TagProp模型[20]。与本文方法最接近的图像标注方法包括：NMF模型[13]、GNMF模型[14]、基于结构化组稀疏的多标注学习模型(Multi-label Boosting with structural Grouping Sparsity, MtBGS)[6]、结合组稀疏与图正则化的LJGL模型[7]。前两种模型是非负分解方法，后3种模型是结合组稀疏的图像标注模型。与MtBGS模型相比，LJGL模型和GRNGS模型在其基础上增加了图正则化项。而与LJGL模型相比，GRNGS模型则又进一步结合了模型的非负参数约束，使得模型学习过程更加符合人脑的认知模式。表2和表3给出了各方法的标注结果。

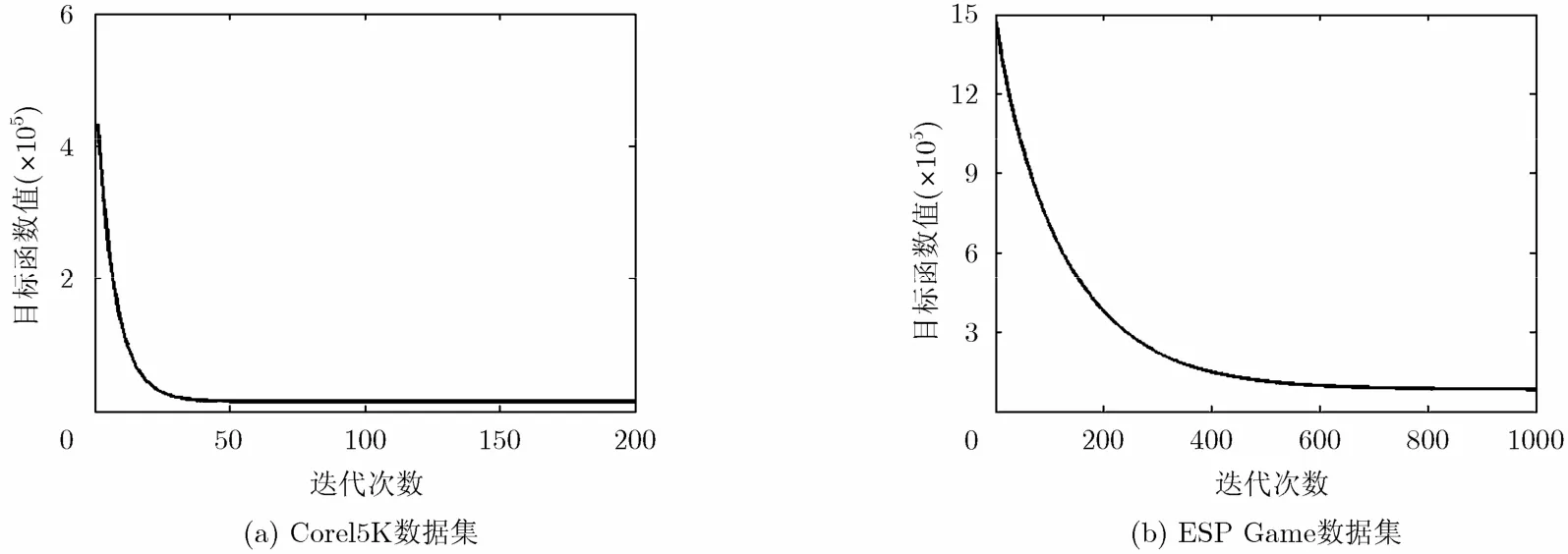
图4 非负迭代算法的收敛过程

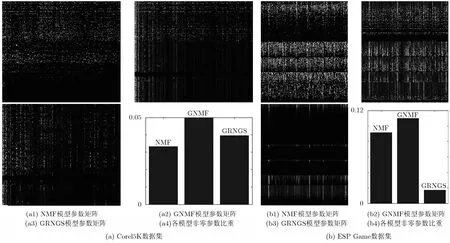
图5 模型参数及其稀疏性分析

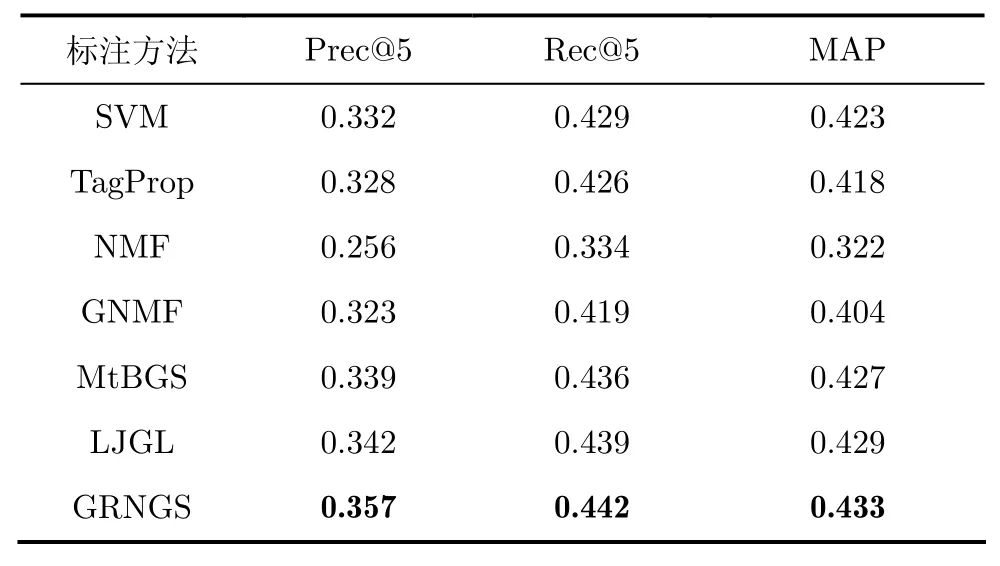
表 2 Corel5K数据集上的标注结果比较

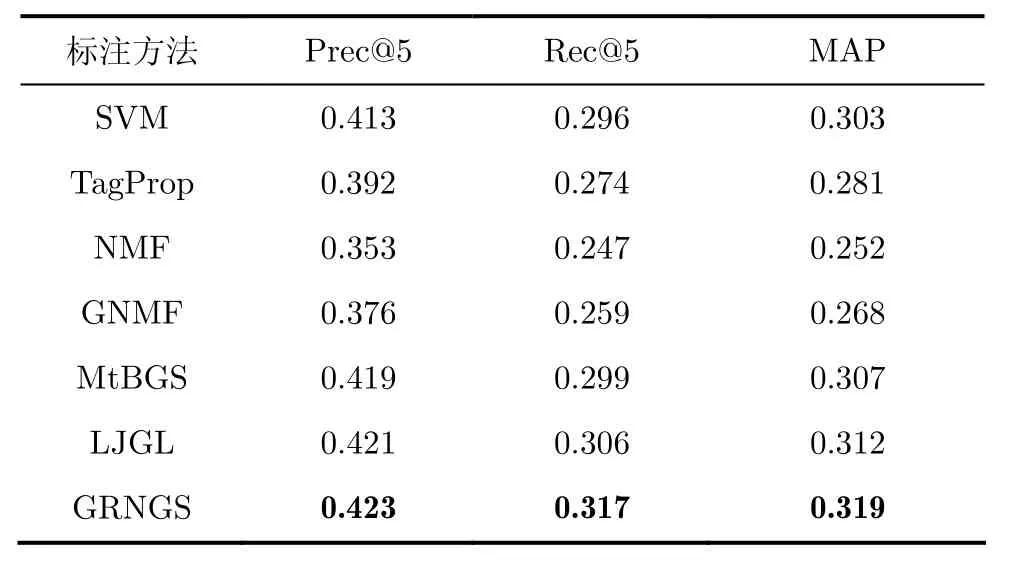
表 3 ESP Game数据集上的标注结果比较

从实验结果中可以看出，在Corel5K和ESP Game数据集上，将结合组稀疏的标注模型(如MtBGS, LJGL和GRNGS)相较于其他标注模型(如SVM, TagProp, NMF和GNMF)在实验结果上有了一定的提高，这充分说明了组稀疏对图像高层语义理解有着重要的意义。通过比较MtBGS, LJGL和GRNGS在两个数据集上的标注结果，我们可以发现LJGL模型的标注结果相较于MtBGS的标注结果提高较少，这说明单一的流形约束并不能够显著地提高模型对图像语义的理解；而本文方法在组稀疏和图正则化的基础上又进一步考虑了模型参数的非负性约束条件，使得标注结果相较于其他模型有了较为显著的提高。

4 结束语

本文研究了组稀疏、图正则化以及非负参数约束对图像标注的影响，提出了GRNGS模型来构建多种异构视觉特征与图像语义标签之间的映射关系。实验结果表明，本文方法具有较好的稳定性和良好的标注性能。在今后的工作中，我们将侧重研究不同视觉特征在核映射空间上的自适应距离测度，并从层次化语义角度进一步改善“语义鸿沟”问题的解决方案。

[1] Wright J, Ma Y, Mairal J, et al.. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044.

[2] Shen L, Yeo C, and Hua B. Intrinsic image decomposition using a sparse representation of reflectance[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(12): 2904-2915.

[3] 宋相法, 焦李成. 基于稀疏编码和集成学习的多示例多标记图像分类方法[J]. 电子与信息学报, 2013, 35(3): 622-628.

Song Xiang-fa and Jiao Li-cheng. A multi-instance multi-label image classification method based on sparse coding and ensemble learning[J]. Journal of Electronics & Information Technology, 2013, 35(3): 622-628.

[4] Wu F, Han Y, Liu X, et al.. The heterogeneous feature selection with structural sparsity for multimedia annotation and hashing: a survey[J]. International Journal of Multimedia Information Retrieval, 2012, 1(1): 3-15.

[5] Wu F, Han Y, Tian Q, et al.. Multi-label boosting for image annotation by structural grouping sparsity[C]. ACM International Conference on Multimedia, Firenze, Italy, 2010: 15-24.

[6] Yang Y, Huang Z, Yang Y, et al.. Local image tagging via graph regularized joint group sparsity[J]. Pattern Recognition, 2013, 46(5): 1358-1368.

[7] Gao S, Chia L T, Tsang I W H, et al.. Concurrent single-label image classification and annotation via efficient multi-layer group sparse coding[J]. IEEE Transactions on Multimedia, 2014, 16(3): 762-771.

[8] Jayaraman D, Sha F, and Grauman K. Decorrelating semantic visual attributes by resisting the urge to share[C]. IEEE Conference on Computer Vision and Pattern Recognition, Columbus, USA, 2014: 1629-1636.

[9] Bahrampour S, Ray A, Nasrabadi N M, et al.. Quality-based multimodal classification using tree-structured sparsity[C]. IEEE Conference on Computer Vision and Pattern Recognition, Columbus, USA, 2014: 4114-4121.

[10] Cho J, Lee M, Chang H J, et al.. Robust action recognition using local motion and group sparsity[J]. Pattern Recognition, 2014, 47(5): 1813-1825.

[11] Yogatama D and Smith N A. Making the most of bag of words: sentence regularization with alternating direction method of multipliers[C]. International Conference on Machine Learning, Beijing, 2014, Vol. 32: 656-664.

[12] Yan L, Yan L, Xue G R, et al.. Coupled group lasso for web-scale CTR prediction in display advertising[C]. International Conference on Machine Learning, Beijing, 2014: 802-810.

[13] Lee D D and Seung H S. Learning the parts of objects by nonnegative matrix factorization[J]. Nature, 1999, 401(6755): 788-791.

[14] Cai D, He X, Han J, et al.. Graph regularized nonnegative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1548-1560.

[15] Zhou B, Zhang F, and Peng L. Compact representation for dynamic texture video coding using tensor method[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2013, 23(2): 280-288.

[16] Müller H, Marchand-Maillet S, and Pun T. The truth about corel-evaluation in image retrieval[C]. ACM International Conference on Image and Video Retrieval, London, UK, 2002, Vol. 2383: 38-49.

[17] Von Ahn L and Dabbish L. Labeling images with a computer game[C]. Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, New York, USA, 2004: 319-326.

[18] Zhou N, Cheung W K, Qiu G, et al.. A hybrid probabilistic model for unified collaborative and content-based image tagging[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(7): 1281-1294.

[19] Oliva A and Torralba A. Modeling the shape of the scene: a holistic representation of the spatial envelope[J]. International Journal of Computer Vision, 2001, 42(3): 145-175.

[20] Guillaumin M, Mensink T, Verbeek J, et al.. TagProp: discriminative metric learning in nearest neighbor models for image auto-annotation[C]. International Conference on Computer Vision, Kyoto, Japan, Sept. 2009: 309-316.

钱智明： 男，1986年生，博士，研究方向为图像理解与目标识别.

钟 平： 男，1979年生，副教授，研究方向为图像理解与目标识别.

王润生： 男，1941年生，教授，研究方向为图像理解与目标识别.

Automatic Image Annotation via Graph Regularization and Non-negative Group Sparsity

Qian Zhi-ming Zhong Ping Wang Run-sheng
(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Extracting an effective visual feature to uncover semantic information is an important work for designing a robust automatic image annotation system. Since different kinds of heterogeneous features (such as color, texture and shape) show different intrinsic discriminative power and the same kind of features are usually correlated for image understanding, a Graph Regularized Non-negative Group Sparsity (GRNGS) model for image annotation is proposed, which can be effectively solved by a new method of non-negative matrix factorization. This model combines graph regularization with l2,1-norm regularization, and is able to select proper group features, which can describe both visual similarities and semantic correlations when performing the task of image annotation. Experimental results reported over the Corel5K and ESP Game databases show the robust capability and good performance of the proposed method.

Image annotation; Graph regularization; Group sparsity; Non-negative matrix factorization

TP391

： A

：1009-5896(2015)04-0784-07

10.11999/JEIT141282

2014-10-09收到，2014-12-30改回

国家自然科学基金(61271439)资助课题

*通信作者：钟平 zhongping@nudt.edu.cn