时频面滑窗掩膜的多分量信号高效重构算法

粟 嘉陶海红 饶 烜 谢 坚

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

时频面滑窗掩膜的多分量信号高效重构算法

粟 嘉*陶海红 饶 烜 谢 坚

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

针对基于特征值分解的Wigner-Ville分布信号重构算法运算复杂度高这一问题，该文提出一种高效多分量信号重构算法。首先，通过分析Wigner-Ville逆变换公式，推导出瞬时时刻重构序列与原序列之间的联系，提出一种高效的信号重构算法。然后，采用平滑伪Wigner-Ville分布作为时频掩膜抑制Wigner-Ville分布的交叉项，并通过在时频面内滑窗的方法逐一提取各分量信号。最后，结合高效信号重构算法和时频面滑窗掩膜技术，实现多分量信号快速准确重构。仿真实验证明了该算法的有效性和可行性。

信号处理；信号重构；Wigner-Ville分布；时频掩膜；多分量信号

1 引言

在雷达、通信和声呐等工程应用中，接收到的信号由来自不同发射源的信号、杂波及噪声组成，而这些多分量信号往往在时域或是在频域都是交叠的[1,2]。为了检测、识别各个信号的分量，需要对接收的信号进行有效地分析。在实际工程应用中，多分量信号往往是时变的，因此时频分析成为了一种有效的分析工具[3−5]。最常用的时频分析工具是短时傅里叶变换(Short-Time Fourier Transform, STFT)，但该方法无法同时兼顾信号的时域和频域分辨力。而Wigner-Ville分布(Wigner-Ville Distribution,WVD)以其良好的时频聚集性在雷达、声呐等领域得到了广泛的应用；但对时变的多分量信号处理时会产生交叉项，严重干扰真实信号的特征，阻碍信号的分析和各分量信号的提取[6,7]。此外，在一些应用场合，例如目标与杂波的分离、微动特征的提取等，仅仅检测和识别各分量的时频信息是不够的，还需要精确重构出各分量信号[8−15]。

多分量信号的重构方法大致可以分为两大类：参数化方法和非参数化方法。参数化方法通常通过最小均方(Least Mean Square, LMS)准则、最大似然(Maximum Likelihood, ML)准则以及自适应投影等方法逐个估计各信号分量的频率、相位和幅度等参数，从而实现各分量信号的重构[8−11]。在实际的信号模型与假设的模型匹配且模型参数精确估计条件下，参数化方法理论上是最优的。但是在实际情况中，信号的数学建模比较复杂，模型不匹配或者参数估计存在误差时都会导致信号重构不准确，并且参数化方法需要高维参数搜索，计算复杂度高。另一类方法是非参数化方法，其基本思想是寻找一信号，使其时频分布在最小二乘意义下逼近给定的时频模型[12−15]。文献[13]给出了一种S-Method (SM)，该方法结合了短时傅里叶变换线性特性和WVD高时频分辨率的优点，在保持良好时频分辨率基础上，能够有效地消除交叉项的影响。基于SM信号重构算法是利用多分量信号的SM时频分布等于各自分量WVD之和这一特性，采用特征值分解方法依次实现各分量信号的重构。但该重构算法计算复杂度高，并且当参数L选取不当时，信号能量会分散到多个特征值上，从而造成重构信号的能量损失。文献[14]提出一种基于WVD时频遮隔的信号分解算法，采用其它无交叉项或交叉项较小的时频分布作为掩膜，通过设置阈值的方法构建时频支撑区域，并对时频遮隔后的逆WVD进行特征值分解，实现多分量信号的重构。该方法在计算自相关矩阵时，需要对WVD进行近似插值，且矩阵中的元素需逐一计算，计算复杂度高制约了其在实际中的应用。文献[15]采用STFT作为时频掩膜来抑制WVD产生的交叉项，并在基于特征值分解的信号重构算法基础上，提出了一种快速信号重构方法(Fast Signal Synthesis Method, FSSM)，该方法在计算矩阵自相关矩阵时，采用了快速傅里叶变换(Fast Fourier Transformation, FFT)和矩阵重排技术，避免了矩阵元素的逐一计算，但该方法在重构信号时仍需要特征值分解操作，以致算法复杂度较高。针对以上问题，本文提出一种基于时频面滑窗掩膜的多分量信号高效重构算法，利用重构序列与原序列的关系，实现单分量信号的快速准确地重构，考虑到重构算法本身的特点，采用平滑伪Wigner-Ville分布抑制WVD的交叉项，并结合时频面滑窗掩膜方法逐一提取多分量WVD的自项，最终实现多分量信号的重构。

2 基于特征值分解的信号重构算法

N点离散序列x(n)的离散WVD可以表示为[14,15]

将n1=n+m和n2=n−m代入式(1)，则WVD的逆变换可以表示为

其中，n1,n2∈[1,N]是正整数，R(n1,n2)的矩阵形式可以表示为

其中，x是由序列元素构成的列向量，可表示为x =[x(1) x(2) x(3) … x(N )]T。对矩阵R进行特征值分解：

其中，λi, ui分别为矩阵R的特征值和特征向量。对比式(3)和式(4)可知矩阵R的秩为1，只有一个非零特征值，因此序列x表示为

式中，ϕ为常数相位。由式(2)可知当(n1+n2)/2不为整数时，则需要通过插值操作得到WDx((n1+ n2)/2,k)，插值会引入误差，导致重构的信号不精确，而矩阵R中的元素均需要逐一计算，且信号重构还需要进行特征值分解操作。FSSM在计算矩阵R时采用了FFT和矩阵重排技术，避免了矩阵元素的逐一计算，但信号重构仍需要进行特征值分解，导致信号重构算法计算复杂度高。

3 高效的多分量信号重构算法

其中，n∈[1,N], n'∈[1,2N]。序列f(n')由序列x(n)相邻元素间补零构成。序列f(n')的WVD变换可表示为

为克服基于特征值分解的信号重构方法出现的问题，本文首先提出一种高效的单分量信号重构算法，然后采用基于时频面滑窗掩膜方法，实现多分量信号准确快速重构。

3.1 高效信号重构算法

为避免传统信号重构算法中的插值操作引入的误差，首先构建一个新的序列f(n')：

其逆变换可以表示为

对比式(2)和式(9)可知，当n1+n2为奇数时，式(2)需对WDx进行插值操作，而式(9)无论n1+n2为奇数还是偶数，都可直接由WDf(n',k)直接得到x(n1)x*(n2)的值，避免了插值操作引入的误差。

假设n1在区间[1,N]遍历，c是[1,N]内选取的一个参考点，则式(9)可以改写成

式(10)表明，序列x(n)可以由WDf(n,k)唯一重构，其幅度与原信号只相差x*(c)倍。将x(n1)x*(c)元素构成的序列记为序列xˆ,xˆ=[x(1)x*(c) x(2)x*(c)…x(c)x*(c) … x(N)x*(c )]T。假设x(c)=Aejθ，其中A, θ分别为x(c)的幅度和相位，则序列xˆ可以改写成

再对序列两边乘以ejϕ得

其中，ϕ是搜索相位，在(0,2π]范围内变化。当ϕ=θ时，序列xˆ与序列x相等，即

其中，相位搜索可采用能量最小准则：

3.2 基于时频面滑窗的掩膜方法

将高效的信号重构方法推广至多分量信号重构时，两个方面因素制约了其在多分量信号重构中的应用：一方面多分量WVD不可避免地会产生交叉项，另一方面该方法只适用于单分量信号的重构。针对交叉项问题，可以采用阈值法构建时频掩膜抑制交叉项[14,15]，由于平滑伪WVD能在一定程度抑制交叉项且时频分辨率接近WVD，因此本文以平滑伪WVD作为掩膜。针对高效信号重构方法只适用于单分量信号重构问题，则要求在时频掩膜后只保留单个分量的WVD。此时可以分两种情况讨论：情况1是当两个信号能量差别比较大时，可以通过设置高门限的方法从弱分量中提取强信号分量；情况2是当两个信号能量比较接近时，若仍采用高门限的方法，则难以实现各信号分量逐一提取。针对第2种情况，提出了基于时频面滑窗的掩膜方法，该方法同样适用于第1种情况。多分量信号时频面滑窗掩膜及重构算法步骤为：

步骤1 根据式(6)构建新序列f(n')，其中n'∈[1,2N], N为雷达回波信号长度；

步骤 2 计算新信号f(n')的平滑伪Wigner-Ville分布WDSP(n,k)，并在时频平面内搜索最大值，分别记录最大值对应的频率和时域位置k1, n1，以k1为中心在频率上加上一个长度为L的窗，其中B/2＜L≤B, B为平滑伪WVD瞬时谱宽，频率加窗如图1(a)虚线所示，在窗内通过设置门限得到n1时刻的支撑区域MWDSP(n1,k)。

其中，门限值m可以定义为

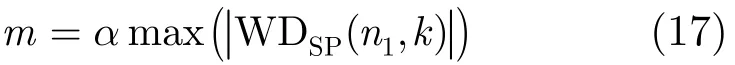
式中，max(|WDSP(n1,k)|)为窗内|WDSP(n1,k)|的最大值，α为门限调节因子，0＜α＜1；

步骤3 将窗平行滑动到下一个时刻n2，如图1(b)中虚线窗所示，在窗内搜索最大值并记录对应的频率位置k2，再以k2为中心重新构建一个长度为L窗(图1(b)实线窗)，并计算n2时刻的支撑区域MWDSP(n2,k)。重复以上操作直到获得每一时刻的时频支撑域MWDSP(n,k)；

步骤4 计算f(n')的Wigner-Ville分布WD(n,k)，并与MWDSP(n,k)相乘，得到掩膜后的Wigner-Ville分布MWD：

步骤5 根据式(10)得到新序列xˆ中的全部元素，再根据式(12)～式(15)对序列进行归一化和相位搜索处理，快速重构多分量中时频能量最强的一个分量信号x1；

步骤6 将强分量信号x1从原始多分量信号中减去，得到剩余信号xr，将剩余信号重复以上步骤，直到时频分布能量的最大值小于设定门限为止。

3.3 门限调节因子和窗长的选取

图1 基于时频面滑窗的动态门限设置方法

图2 RMSE随门限调节因子与窗长的变化关系

门限调节因子α和窗长L(频点个数)选取会影响信号重构质量。当门限调节因子选取得过小或者窗选取得过长，掩膜后的WVD会包含大量的噪声成分；反之，掩膜后的WVD会损失部分有用信号，这两种情况均会造成信号重构精度下降。图2(a)给出了均方根误差(Root Mean Square Error, RMSE)与门限调节因子的关系，当门限调节因子在0.05～0.40范围内选取时，RMSE变化不大，当α超过0.4后信号重构质量急剧下降，由局部放大图可知，门限调节因子取0.1时信号重构质量最佳。图2(b)反映了RMSE与窗长的关系，随着窗的增大，支撑域包含的有用信号也逐渐增多，信号的重构质量也逐渐提高；当窗长大于8后，支撑域包含的噪声分量会随着窗的增大而逐渐增多，影响信号的重构质量；当窗长为8时信号重构误差最小。因此，本文中门限调节因子α取0.1，窗长L取8。

4 计算机仿真与性能分析

4.1 实验1：无噪声情况下信号重构分析

假设多分量信号x(n)由两个分量x1(n)和x2(n)构成，即

其中

多分量信号的WVD及平滑伪WVD如图3(a)、图3(b)所示，由图可以看出，WVD存在交叉项，但自项具有良好的时频分辨率，而平滑伪WVD抑制了交叉项，但时频分辨率低于WVD，因此以平滑伪WVD作为掩膜能够实现自项提取和交叉项抑制的目的。图3(c)给出了采用高门限值提取强信号分量方法的时频支撑域，其中门限调节因子α=0.6，由图可知强信号分量1和部分强分量2同时被提取，则重构的信号频谱如图3(d)所示，其中重构的信号为两个分量信号之和，这将导致基于WVD的高效信号重构算法无法实现信号分离。而采用基于时频面滑窗的掩膜方法，能够逐一提取各信号分量，以分量1为例，其时频支撑域及重构的时域信号如图3(e)、图3 (f)所示。在不存在噪声时，重构的信号与原信号很好地吻合。

4.2 实验2：噪声背景下信号重构性能分析

假设混合信号由两个时频平面交叉的分量x1(n)和x2(n)组成：

图3 基于时频平面滑窗掩膜的多分量信号高效重构方法

图4 多参考点与单一参考点比较

其中，混合信号的信噪比为(SNR)为0 dB。混合信号的WVD、分量1的时频掩膜及采用单一参考点重构的信号时域图如图4(a)～图4(c)所示。信号重构质量与参考点信号能量密切相关，由式(12)可知序列归一化处理是以为基准，当参考点的重构信号能量等于实际信号能量时，则重构信号质量最佳，因此在不考虑噪声的情况时，以时频支撑域内任意有效时刻作为参考点均能准确地重构信号。但在噪声环境中，以随机的单一参考点重构的信号会随噪声的起伏偏大或偏小。因此，需采用多参考点平均的方法，分别计算M个有效参考点重构的信号序列并求其平均。

其中，xm(n)表示第m个参考点重构的信号序列。所求序列(n)更接近原始信号，如图4(d)所示，其中参考点个数为20。图4(e)给出了3种算法的比较，其中高效重构算法采用了时频面滑窗掩膜方法构建时频支撑域，而特征值分解和FSSM采用了阈值法构建时频支撑域。由图可以看出，有效参考点个数选取的越多、SNR越大，RMSE就越小，当SNR低于-2 dB时，单个参考点重构信号的质量受噪声影响比较大，其RMSE要略大于其它两种方法，但随着SNR和有效参考点个数的增加，本文算法要优于其它两种算法。表1给出了3种重构算法的计算复杂度分析。从表中可以看出，高效信号重构算法需要对补零后长度为2N的新序列f(n')进行Wigner-Ville变换，虽然该步骤会增加计算复杂度，但与N点Wigner-Ville变换的计算复杂度为同一量级。所提算法的优势在于该算法避免了矩阵R的计算与特征值分解等操作(特征值分解重构算法的矩阵计算复杂度为N3量级，FSSM矩阵计算复杂度为N2log2N量级，两种方法的特征值分解计算复杂度为N3量级)，只需要计算M个有效参考点重构的信号序列xm(n)并取其平均，其计算复杂度为MN2量级(M≪N)。因此，高效信号重构算法能够有效降低计算复杂度，并随着序列长度N的增加，速度优势会显著提高。

表1 3种方法的计算复杂度

5 结束语

本文提出了一种基于时频平面滑窗掩膜的多分量信号高效重构算法，采用时频滑窗掩膜和快速的信号重构算法实现多分量信号的逐一提取与重构。仿真实验表明本文提出算法能快速准确地实现多分量信号的重构。该算法能够实现信号分析、参数估计及信号提取，并能够推广到信号与杂波和干扰分离及微动目标提取等方面。

[1] Stankovic L J. Multicomponent signal decomposition based on chirplet pursuit and genetic algorithms[J]. IEEE Transactions on Signal Processing, 1994, 42(1): 225-229.

[2] Zheng J, Su T, Zhu W, et al.. ISAR imaging of targets with complex motions based on the keystone time-chirp rate distribution[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1275-1279.

[3] Francos A and Porat M. Analysis and synthesis of multicomponent signals using positive time-frequency distributions[J]. IEEE Transactions on Signal Processing, 1999, 47(2): 493-504.

[4] Chen G and Wang Z. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J]. Mechanical Systems and Signal Processing, 2012, 28: 258-279.

[5] 卢振坤, 杨萃, 王金炜. 基于 Gabor 变换的超声回波信号时频估计[J]. 电子与信息学报, 2013, 35(3): 652-657. Lu Zhen-kun, Yang Cui, and Wang Jin-wei. Gabor transform based time-frequency estimation of ultrasonic echo signal[J]. Journal of Electronics & Information Technology, 2013, 35(3): 652-657.

[6] Zheng L, Shi D, and Zhang J. CAF-FrFT: a center-affinefilter with fractional Fourier transform to reduce the crossterms of Wigner distribution[J]. Signal Processing, 2014, 94: 330-338.

[7] Chen G, Chen J, and Dong G M. Chirplet Wigner-Ville distribution for time-frequency representation and its application[J]. Mechanical Systems and Signal Processing, 2013, 41(1): 1-13.

[8] Trintinalia L C and Ling H. Joint time-frequency ISAR using adaptive processing[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(2): 221-227.

[9] Trintinalia L C, Bhalla R, and Ling H. Scattering center parameterization of wide-angle backscattered data usingadaptive Gaussian representation[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(11): 1664-1668.

[10] Francos A and Porat M. Parametric estimation of multicomponent signals using minimum cross entropy timefrequency distributions[C]. Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis, Paris, France, 1996: 321-324.

[11] Zanjireh Y, Rezaie A H, and Amindavar H. Multi component signal decomposition based on chirplet pursuit and genetic algorithms[J]. Applied Acoustics, 2013, 74(12): 1333-1342.

[12] Hlawatsch F and Krattenthaler W. Bilinear signal synthesis[J]. IEEE Transactions on Signal Processing, 1992, 40(2): 352-363.

[13] Stankovic L J, Thayaparan T, and Dakovic M. Signal decomposition by using the S-method with application to the analysis of HF radar signals in sea-clutter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4322-4342.

[

[15] Zuo L, Li M, Zhang X, et al.. An efficient method for detecting slow-moving weak targets in sea clutter based on time-frequency iteration decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3659-3672.

粟 嘉： 男，1985年生，博士生，研究方向为信号处理、时频分析、动目标检测.

陶海红： 女，1976年生，博士，博士生导师，教授，研究方向为雷达信号处理、阵列信号处理、动目标检测.

饶 烜： 男，1977年生，博士生，研究方向为动目标检测、目标跟踪.

An Efficient Multi-component Signals Reconstruction Algorithm Using Masking Technique Based on Sliding Window in Time-frequency Plane

Su Jia Tao Hai-hong Rao xuan Xie Jian
(National Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China)

Due to the huge computation for eigenvalue decomposition based signal synthesis method, an efficient multi-component signals reconstruction algorithm is presented in this paper. Firstly, by analyzing the inverse transformation for Wigner-Ville distribution, a fast signal reconstruction is developed using the inherent relationship between original signal and synthesized signal. Then, the smoothed pseudo Wigner-Ville distribution is used as a time-frequency masking to suppress the cross-terms, and the sliding window method in time-frequency plane is adopted to extract signals one by one. Finally, by combining the signal synthesis algorithm and the sliding window masking method, multi-component signals reconstruction can be realized efficiently and accurately. Simulation results demonstrate the effectiveness and feasibility of the proposed algorithm.

Signal processing; Signal reconstruction; Wigner-Ville distribution; Time-frequency masking; Multicomponent signal

TN911.7

： A

：1009-5896(2015)04-0804-07

10.11999/JEIT140511

2014-04-22收到，2014-08-04改回

国家973计划项目(2011CB707001)，国家自然科学基金(60971108)，航空基金和西安电子科技大学基本科研业务费(BDY061428)资助课题

*通信作者：粟嘉 Jiasu1011@126.com