稳健收敛的时差频差定位技术

房嘉奇冯大政 李 进

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

稳健收敛的时差频差定位技术

房嘉奇*冯大政 李 进

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

为实现对目标位置和速度的精确定位，该文提出一种基于正则化理论的时差频差定位技术。该算法首先利用最大似然方法确定目标函数，然后通过传统牛顿法对目标位置和速度进行迭代求解。众所周知传统牛顿法对初始值要求较高，较差初始值会导致Hess矩阵趋于病态，从而致使迭代发散，该文引入正则化理论修正Hess矩阵，使其更加合理，保证算法稳健收敛。实验结果表明：相对于传统牛顿法，该文算法在初始值的选取上具有稳健性，对误差选取较大的初始值，仍能够保证算法的收敛性；相对于现有闭合式定位方法，该文算法在噪声较大时具有较好的定位精度，定位精度接近于Cramer-Rao界，具有广泛的实用价值。

无源定位；到达时差；到达频差；传统牛顿法；Hess矩阵；正则化算法

1 引言

对未知目标的无源定位问题，由于其在导航，跟踪测轨，无线传感器网络，移动通信等方面的广泛应用，一直都是信号处理领域的研究热点。目前常用的无源定位技术可以分为到达角度(Angle Of Arrival, AOA)、到达时间(Time Of Arrival, TOA)、到达时间差(Time-Difference-Of-Arrival, TDOA)、到达频差(Frequency-Difference-Of-Arrival, FDOA)等方法。对于固定的目标辐射源来说，时差(TDOA)定位技术利用目标到两个基站的到达时差信息确定一条以两基站为焦点的双曲线，通过多个基站的TDOA测量值确定多条双曲线，其交点为目标位置。时差定位技术由于不需要目标与基站的合作关系且成本较低，因而在现实中得到广泛的应用。在现代定位问题中，目标辐射源时常处于运动状态，而接收机也多装载于汽车，飞机，卫星等移动平台中。因此，需要在时差定位的基础上引入到达频差(FDOA)技术来联合估计目标的位置以及速度。

估计目标的位置和速度并不简单，因为其需要求解的时差，频差等式是非线性的。最大似然估计能够对非线性问题能够提供渐进无偏解，但它需要大量的搜索，在实际中需要耗费大量的计算，难以实现。一个普遍的做法就是通过泰勒展开式(Taylor-Series, TS)将时差频差非线性等式线性化[1]，这种方法要求初始值必须具备良好的精度才能够保证迭代收敛。基于这个缺点，一些闭合式解法被提出用于求解非线性的时差频差方程[2−13]，其中广泛使用的两步WLS(Weighted Least Squares)算法[2−5]引入关于目标位置的附加参数，采用二次最小二乘算法给出了定位方程组的非迭代解析解，特点是计算量小，在噪声较小且服从高斯分布的环境下定位精度高，但当噪声测量误差较大时，该算法的性能会显著下降。近年来兴起的SDP(Semi-Definite Programming)技术[14,15]利用凸优化方法对目标初始位置进行求解，然后通过迭代确定目标位置，该方法计算量较大，如果初始值不够精确，目标位置可能陷入局部最小解中。

在噪声较大的情况下，由于时差频差等式的非线性特点，闭合式算法和SDP算法所求得的目标位置，速度会存在较大误差，而运用传统牛顿法进行迭代求解时，又会因为较差的初始值而导致迭代发散。本文在传统牛顿法的基础上，提出了一种基于正则化理论的时差频差定位技术。由时差频差测量信息可知，求解目标位置不需要用到目标的速度信息，而求解目标的速度则需要用到目标的位置信息，针对这一特点，本文利用最大似然估计建立目标函数，首先运用传统牛顿法对目标位置进行迭代求解，引入正则化理论修正迭代过程中因为初始值差导致的病态Hess矩阵，从而使算法在初始值的选取上具有稳健性，保证迭代收敛。然后再次运用传统牛顿法对目标位置和速度进行联解，求得目标的速度的同时进一步精确目标的位置。本文算法有以下优点：(1)对目标位置，速度初始值的选取具有强大的稳健性，在初始值较差的情况下仍能准确的搜索到目标的位置，速度。(2)在测量噪声较大时相对于闭合式算法具有更高的定位精度，定位误差接近Cramer-Rao界。

2 系统模型

在多站无源时差频差定位系统下，假设待测目标辐射源位置x=[x,y,z]T，速度，第i个已知接收基站的位置si=[xi,yi,zi]T，速度=,i=1,2,…,M ,M为参与定位基站数目，在3维空间内至少需要4个基站来产生3组TDOA和FDOA值来确定目标的位置和速度。为了获得目标位置和速度的唯一解，接收基站不能设置在一个点

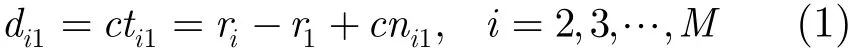
其中ir为目标和第i个接收基站之间的距离。或者一条直线上。不考虑非视距传播的影响，以第1个接收基站为中心基站，则第i个基站和第1个基站之间的TDOA测量值为

c为电波传播速度，ti1为第i个基站和第1个基站之间的TDOA测量值，di1为与其对应的测量距离差(Range-Difference-Of-Arrival, RDOA),ni1为TDOA测量值中的噪声，文中用RDOA来代替TDOA，因为其在本质上只是相差了一个常数乘子c。对式(1)求导可得到第i个基站和第1个基站之间FDOA测量值。

测得的频差需要在式(3)中乘以常数fc/c, fc表示目标载波频率，实际中忽略fc/c不影响定位精度。在通常情况下，检测到得TDOA, FDOA测量值分别服从零均值，方差为,的高斯分布，并且二者之间相互独立。将TDOA, FDOA测量等式方程组采用向量形式表达为

其中d=[d21,d31,…,dM1]T,f=[d.21,d.31,…,d.M1]T, r =[r1,r2,…,rM]T,r.=[r.1,r.2,…,r.M]T,G为第1列均为-1的1×(M−1)的列向量与维数为M-1的单位矩阵所合并的(M−1)×M的矩阵，nt=c·[n21,n31,…, nM1]T ,。利用最大似然估计准则，令θ=[xT,x.T]T，目标函数可写为

其中Qt,Qf为TDOA, FDOA测量值的协方差矩阵。由式(1)和式(3)可知目标位置信息仅由多个TDOA测量值获得，与测量的频差信息无关，而求解目标的速度则需要利用目标的位置信息，因此在求解式(7)之前，先根据式(8)：

对目标位置进行求解，将结果作为目标位置的初始值，再通过式(7)对目标速度进行求解，同时再次完善目标位置。本文算法这么做的目的在于：通过分步计算解决了式(7)中的位置，速度双重变量的初始值选取难题(位置或速度任何一个变量的初始值较差都可能导致迭代发散)，使算法对位置，速度初始值的选取都具有强大的稳定性，保证迭代收敛。在每一次迭代中通过求解目标函数的局部最小二乘解(LS)来改进估计值，直到搜索到正确解上。每次迭代的改变量为

每次迭代后新的迭代点xk+1可表示为

3 正则化算法

式(7)和式(8)中的梯度向量和Hess矩阵∇f1(θ)，∇2f1(θ)和∇f2(x),∇2f2(x)可表示为

本文利用传统牛顿法对目标位置，速度信息进行求解，牛顿法是一种需要初始估计值的迭代算法，

由式(2)，式(4)可以得到

本文算法先利用式(8)求解目标位置，然后将求得的目标位置代入式(7)求解目标位置和速度。因为目标的速度信息与目标的位置信息有很大关系，而一般情况下FDOA噪声功率又比TDOA噪声功率小的多，因此如果式(8)求得的目标位置信息较为精确，给出的速度初始值即使误差较大，式(7)仍然能够通过牛顿法快速准确地搜索出目标的位置及速度。 因此，本文将关注的重点集中在对目标位置的求解上，只要能够对目标位置进行精确估计，目标的速度也能够随之被精确算出。

在求解式(8)时，传统的牛顿算法必须要求目标位置具有良好的初始值估计，当初始值和目标真实位置相距较近时，Hess矩阵为正定矩阵，其迭代方向为下降方向，因此传统牛顿法能够准确地搜索到得到目标的真实位置。然而，当目标初始值和目标真值相距较远时，Hess矩阵趋于病态，从而导致其逆矩阵不准确，致使算法迭代发散。导致Hess矩阵病态的原因有两点：(1)Hess矩阵的特征值逐渐降低且趋近于零。(2)矩阵的条件数，即最大特征值和最小特征值之间的比率较大。本文通过公式量化分析Hess矩阵病态原因并且提出改进方法，根据式(13)和式(14)令A=∇2f2(x), b =−∇f2(x)， 因为Hess矩阵为对称矩阵，对矩阵A做SVD分解可得

其中U为单位正交矩阵UTU=In, Σ=diag(σ1, σ2,…,σn),σi和向量ui为特征值和与其相对应的特征向量，由式(9)本文得到迭代的改变量：

因为式(22)中小特征值σi所对应的傅里叶系数|b|的下降速度并不如这些特征值的下降速度快，因此每次迭代的改变量Δx受小特征值所对应项的影响较大。作为结果，Δx会表现出许多符号改变以及随机特征，为了保证迭代中Δx的正确性，就需要减低或者滤出Δx中小特征值所对应的那部分输出的贡献。本文引用正则化理论知识[16]，对病态的Hess矩阵进行修正，将式(22)的问题转化为

令式(23)的代价函数最小来求得修正解Δx，正则化的方法有很多种，本文选择常用的对角加载DSVD方法来修正Hess矩阵，则式(22)可修正为

修正后的矩阵变的更加合理，矩阵条件数降低，其逆矩阵不再出现符号变化以及随机特征， 式(23)和式(24)中λ为重要的正则化参数，用来控制式(23)中前项(数据能量)与后项(稳定能量)之间的比例。所有的正则化方法都需要确定合理的参数λ保证算法快速准确地收敛，本文引入著名的L曲线(L-curve)理论[17]来确定λ，该方法将作为变量取对数画图，在图中寻找最显著的拐点，根据该拐点，求出其对应的正则化参数λ。实验结果验证了L-curve理论在本文算法中的有效性。本文算法步骤为：

步骤 1 给定初始值x(1),允许误差Δ＞0,置k=1, l=1。

步骤 2 由式(13)，式(14)计算∇f2(x(k))和∇2f2(x(k))。

步骤 4 置k:=k+1，转步骤2。

步骤 5 利用步骤3的输出x作为本次迭代的位置初始值，令θ=[xT,x.T]T，由式(11)，式(12)计算∇f1(θ(l)) 和∇2f1(θ(l))。

步骤 7 置l:=l+1，转步骤5。

4 仿真实验

为了验证本文方法的有效性，实验中采用5个基站来估计目标位置和速度，设置基站1为中心基站，接收基站位置及速度见表1，近距离目标和远距离目标位置分别为(280, 325, 375) m或(2800, 3250, 2750) m，目标速度均设为(-20, 15, 40) m/s。目标位置和速度的均方误差定义为RMSE(x)=。实验中假设TDOA, FDOA测量噪声是不相关的，其协方差矩阵可表示为σ2R和0.1σ2R,σ2为时差测量中噪声的方差，R为对角元素为1其余元素为0.5的矩阵。实验结果为5000次蒙特卡洛实验的平均数据。

表1 接收基站位置及速度

图1，图2给出了本文算法在好初始值和差初始值两种情况下同传统牛顿法的比较结果，本组实验中固定σ2=1。图1中目标位置，速度初始值分别给定为(300, 300, 400) m和(50, 50, 50) m/s，图2中目标位置，速度初始值分别给定为(1000, 1000, 800) m和(2000, 2000, 2000) m/s，图2实验特别选择一个很差的初始值来验证本文算法的稳健性。从图1中可以看出，当目标位置，速度初始值选取较好时，本文算法和传统牛顿法都能准确的得到目标位置，速度的正确解，但当目标位置，速度初始值较差时(图2)，传统牛顿法迭代发散，无法得到目标的真实值，但本文算法凭借其强大的稳定性，依然能够通过迭代获得目标位置，速度的正确解，同时在图2中可以看到，只要求得目标的位置信息足够精确，目标的速度初始值即使偏差很大，依然能够快速准确的收敛。本文算法和传统牛顿法主要的计算量在于矩阵的求逆运算，因此其计算复杂度分别约为O(M1×33+M2×63)和O(N×63)，其中M1, M2表示本文算法步骤1和步骤2的迭代次数，N表示传统牛顿法的迭代次数。由图1可以看到本文算法计算量约为O(13×33+4×63)，传统牛顿法计算量约为O(5×63)，本文算法在初始值良好的情况下计算量要略多于传统牛顿算法，其原因在于当初始值足够好时仍然对Hess矩阵进行修正，阻碍了算法的收敛速度，但本文算法在兼顾了速度，准度的情况下，又具有良好的稳定性，从而适用范围更广，尤其是噪声较大的环境。

图3，图4比较了本文算法同传统牛顿法的迭代收敛概率，在没有先验信息的情况下，目标的初始值不能随机选取，实验中通过目前广泛使用的WLS算法获得目标位置和速度的解作为初始值。从图中可以看出，当噪声较小时由WLS算法得到的目标初始值比较精确，本文算法和传统牛顿法收敛概率较高；然而当噪声较大时，由于定位问题的非线性特征，WLS算法获得的目标位置，速度初始值与真实值的误差逐渐变大，遇到较差的初始值时，传统牛顿法很容易迭代发散，因此收敛概率降低。而本文算法凭借强大的稳定性，仍然能够保证在噪声功率较大情况下的较高的收敛概率。

图5，图6为本文算法在近距离和远距离目标两种情况下同WLS算法[2]，多维标度(Multi-Dimensional Scaling, MDS)算法[6]以及克拉美罗界(CRLB)的比较结果，图中可以看出随着测量噪声误差的增加，由于定位问题的非线性特点，闭合式算法WLS, MDS受到门槛效应的影响，所求得的目标位置，速度解逐渐变差，其误差逐渐变大，不断偏离CRLB界限，而本文算法在噪声较大的情况下，相比于WLS, MDS算法具有更高的定位精度，位置和速度的定位精度达到了CRLB界限。

5 结束语

对于目标的无源时差频差定位问题，本文在传统牛顿法的基础上引入了正则化理论来修正由较差初始值而带来的病态Hess矩阵，通过两次牛顿算法精确的搜索目标的位置，速度。分析和仿真结果表明，本文算法与传统牛顿法相比，解决了长期存在的初始值问题，在初始值较差的情况下仍能够对目标进行精确定位，算法具有强大的收敛性，稳定性。与WLS, MDS等闭合式算法相比，尽管其计算量相对较大(迭代算法特性)，但在噪声较大的情况下定位精度更高，定位误差更接近于Cramer-Rao界。本文算法核心思想在于对传统牛顿法中的Hess矩阵进行修正，对于其他的观测模型TOA, AOA，需要用到传统牛顿法求解目标位置时，该算法均可使用，因此本文算法具有良好的实用价值和广泛的适用范围。

图1 好初始值下本文算法与传统牛顿法性能比较

图2 差初始值下本文算法 与传统牛顿法性能比较

图3 目标位置为(280, 325, 375) m时本文算法与传统牛顿法收敛概率比较

图4 目标位置为(2800, 3250, 2750) m时本文算法与传统牛顿法收敛概率比较

图5 目标位置为(280, 325, 375) m时本 文算法与WLS, MDS算法性能比较

图6 目标位置为(2800, 3250, 2750) m时 本文算法与WLS, MDS算法性能比较

[1] Kovavisaruch L and Ho K C. Modified Taylor-series method for source and receiver localization using TDOA measurements with erroneous receiver positions[C]. IEEE International Symposium on Circuits and Systems, Kobe, Japan, 2005: 2295-2298.

[2] Ho K C and Xu W. An accurate algebraic solution for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2004, 52(9): 2453-2463.

[3] Sun M, Yang L, and Ho K C. Accurate sequential selflocalization of sensor nodes in closed-form[J]. Signal Processing, 2012, 92(12): 2940-2951.

[4] Ho K C. Bias reduction for an explicit solution of source localization using TDOA[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2101-2114.

[5] Wang Y and Ho K C. TDOA Source Localization in the presence of synchronization clock bias and sensor poition erors[J]. IEEE Transactions on Signal Processing, 2013, 61(18): 4532-4544.

[6] Wei H W, Peng R, Wan Q, et al.. Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1677-1688.

[7] Yu H, Huang G, Gao J, et al.. An efficient constrained weighted least squares algorithm for moving source location using TDOA and FDOA measurements[J]. IEEE Transactions on Wireless Communications, 2012, 11(1): 44-47.

[8] Deng B, Xiong J, and Xia C. The feasibility analysis of aerial moving target location based on TDOA/FDOA/DSF Measurements[J]. Procedia Engineering, 2012, 29: 785-790.

[9] Lin L, So H C, Chan F K W, et al.. A new constrained weighted least squares algorithm for TDOA-based localization[J]. Signal Processing, 2013, 93(11): 2872-2878.

[10] Xu B, Sun G, Yu R, et al.. High-accuracy TDOA-based localization without time synchronization[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(8): 1567-1576.

[11] Meng W, Xie L, and Xiao W. Decentralized TDOA sensor pairing in multihop wireless sensor networks[J]. IEEE Signal Processing Letters, 2013, 20(2): 181-184.

[12] Huang J and Wan Q. Analysis of TDOA and TDOA/SS based geolocation techniques in a non-line-of-sight environment[J]. Journal of Communications and Networks, 2012, 14(5): 533-539.

[13] Hara S, Anzai D, Yabu T, et al.. A perturbation analysis on the performance of TOA and TDOA localization in mixed LOS/NLOS environments[J]. IEEE Transactions on Communications, 2013, 61(2): 679-689.

[14] Yang K, Wang G, and Luo Z Q. Efficient convex relaxation methods for robust target localization by a sensor network using time differences of arrivals[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2775-2784.

[15] Wang G and Chen H. An importance sampling method for TDOA-based source localization[J]. IEEE Transactions on Wireless Communications, 2011, 10(5): 1560-1568.

[16] Hansen P C. Regularization tools: a matlab package for analysis and solution of discrete ill-posed problems[J]. Numerical Algorithms, 1994, 6(1): 1-35.

[17] Hansen P C, Jensen T K, and Rodriguez G. An adaptive pruning algorithm for the discrete L-curve criterion[J]. Journal of Computational and Applied Mathematics, 2007, 198(2): 483-492.

房嘉奇： 男，1984年生，博士生，研究方向为无源定位与跟踪.

冯大政： 男，1959年生，教授，博士生导师，研究方向为无源定位、雷达成像、阵列信号处理、盲信号处理、神经网络等.

李 进： 男，1985年生，博士生，研究方向为盲信号处理.

A Robustly Convergent Algorithm for Source Localization Using Time Difference of Arrival and Frequency Difference of Arrival

Fang Jia-qi Feng Da-zheng Li Jin
(National Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China)

To pursue accurate source location and velocity, this paper proposes a method based on the Regularization theory to solve the source localization problem utilizing Time-Difference-Of-Arrival (TDOA) and Frequency-Difference-Of-Arrival (FDOA). The proposed algorithm determines the objective function using the maximum likelihood estimator, and then uses classical Newton method to estimate the source position and velocity in an iterative way. It is known that the Newton method requires a good initial value, and a bad initial value can cause an ill-posed Hess matrix which leads to the iteration divergence. This paper introduces the Regularization theory to modify the Hess matrix to make it more proper, which ensures the iteration convergence. The experiment results show that compared with the classical Newton method, the proposed algorithm is robust to the initial value, and is still able to ensure its convergence even with an inaccurate initial value of large error. Compared with some other closed-form source location methods, the proposed algorithm has better location accuracy in large noise levels which can achieve the Cramer-Rao bound. The proposed algorithm can be widely applied in practice.

Passive location; Time-Difference-Of-Arrival (TDOA); Frequency-Difference-Of-Arrival (FDOA); Newton method; Hess matrix; Regularization algorithm

TN911.7

： A

：1009-5896(2015)04-0798-06

10.11999/JEIT140560

2014-04-30收到，2014-11-24改回

国家自然科学基金(61271293)资助课题

*通信作者：房嘉奇 fangjiaqi123@hotmail.com