分块的有序范德蒙矩阵作为压缩感知测量矩阵的研究

赵瑞珍王若乾 张凤珍 岑翼刚 胡绍海

(北京交通大学信息科学研究所 北京 100044)

(现代信息科学与网络技术北京市重点实验室 北京 100044)

分块的有序范德蒙矩阵作为压缩感知测量矩阵的研究

赵瑞珍*王若乾 张凤珍 岑翼刚 胡绍海

(北京交通大学信息科学研究所 北京 100044)

(现代信息科学与网络技术北京市重点实验室 北京 100044)

测量矩阵是压缩感知(Compressed Sensing, CS)的重要组成部分，确定性的测量矩阵易于硬件实现，但是重构信号的精度一般不如随机矩阵。针对这一缺点，该文提出并构造了一种新的确定性测量矩阵，称作分块的有序范德蒙矩阵。范德蒙矩阵具有线性不相关的性质，在此基础上加上分块操作和对元素进行有序排列得到的分块的有序范德蒙矩阵，实现了时域中的非均匀采样，特别适合于维数较大的自然图像信号。仿真实验表明，对于图像信号该矩阵具有远高于高斯矩阵的重构精度，可以作为实际中的测量矩阵使用。

压缩感知；测量矩阵；线性不相关；非均匀采样；范德蒙矩阵

1 引言

压缩感知(Compressive Sensing, CS)[1−3]是针对稀疏或可压缩信号的压缩采样理论，该理论在信号的获取方式上突破了传统的奈奎斯特采样定理。奈奎斯特采样定理要求采样频率高于采样信号的两倍带宽，而压缩感知要求采样信号是稀疏的或是在变换域是稀疏的，使得压缩感知可以在远小于奈奎斯特采样速率的条件下对信号进行采样的同时对信号进行压缩，因此，压缩感知克服了采样数据量巨

2014-06-30收到，2015-03-03改回

国家自然科学基金(61073079)，中央高校基本科研业务费专项基金(2013JBZ003)，高等学校博士点基金(20120009110008)和教育部新世纪优秀人才支持计划(NCET-12-0768)资助课题

*通信作者：赵瑞珍 rzhzhao@bjtu.edu.cn大，传感元、采样时间以及数据存储空间等物理资源浪费严重的问题。

压缩感知理论主要包括信号的获取和信号的重构两个部分，在这两部分中测量矩阵都起着重要的作用。首先，在信号获取端，测量矩阵的优劣关系着信号测量数目的多少，相对于低劣的测量矩阵，优良的测量矩阵可以在较少的测量数目下达到相同的重构精度。其次，在重构端，在相同的采样率下得到数据，优良的测量矩阵对信号的重构精度要高于低劣的测量矩阵。

在压缩感知之初，测量矩阵普遍采用随机矩阵用于理论研究。随机测量矩阵虽然在理论上完美，但是在硬件实现上非常困难。出于对实际问题的考虑，尤其是在单像素相机[4]研制出之后，大部分学者转向研究确定性的测量矩阵和结构性的测量矩阵。截至目前，国内外学者经过严谨的数学证明和反复的实验验证，已提出多种测量矩阵：确定性测量矩阵中如多项式测量矩阵[5]、基于混沌序列的测量矩阵[6]以及近年来将编码理论用于该领域得到的各种校验码测量矩阵[7,8]，其中多项式测量矩阵和校验码矩阵对稀疏信号重构效果较好，但是对矩阵的行数和列数要求十分严格，而且对可压缩信号重构较差，基于混沌序列的测量矩阵是稠密矩阵，需要占用较多的存储空间；结构性的测量矩阵中如分块压缩感知的测量矩阵[9]、稀疏随机矩阵[10]、托普利兹矩阵[11]、广义轮换矩阵[12]，其中构成分块压缩感知测量矩阵的子矩阵和稀疏随机矩阵是随机矩阵，相对于确定性矩阵来说，硬件实现上仍然困难，托普利兹矩阵和广义轮换矩阵具有一定的结构，减少了存储空间，但是重构精度一般。

针对上述测量矩阵的优缺点，本文提出并构造了一种新的确定性测量矩阵，分块的有序范德蒙矩阵。范德蒙矩阵具有线性不相关的性质[13]，将分块和非均匀采样[12,14]的思想引入其中得到的分块的有序范德蒙矩阵具有了一定的结构性。这种新的测量矩阵占用存储空间少，易于硬件实现，而且仿真实验表明，其对自然图像具有远高于高斯矩阵的重构精度。

2 基本理论

设x是长度为N的稀疏信号，经过线性测量后得到长度为M(M＜N)的观测信号y，它们之间的关系可以表示为：

2.1 压缩感知

其中矩阵Φ称为测量矩阵，大小为M×N。如果x是可压缩信号，可以把x变换到稀疏域中表示，即x=Ψs，其中s是N维的稀疏向量，Ψ是N×N大小的稀疏表示基。把该式代入式(1)得到：

其中矩阵Θ=ΦΨ称为传感矩阵，大小为M×N。

上述过程即为压缩感知的信号获取过程，这个过程是线性的。而信号的重构过程是非线性的，当x是稀疏信号时，重构的数学表达式为

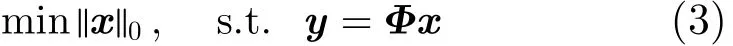
求解式(3)可以直接重构出原始信号x。当x是可压缩信号时，重构的数学表达式为

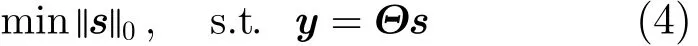
对于式(4)，为了重构出原始信号x，需要把求得的s代入x=Ψs中。由于式(3)和式(4)的l0范数最小化问题是一个NP-hard问题，可以使用l1范数代替求解，具体参见文献[3]。重构过程用到的一些重构算法具体参见文献[15]。

2.2 测量矩阵

从压缩感知的整个过程中可以看出测量矩阵起着关键作用，是压缩感知的重要组成部分。为了能够精确重构信号，文献[2]给出了测量矩阵需要满足的3个特征：(1)由测量矩阵的列向量组成的子矩阵的最小奇异值必须大于一定的常数，也即：测量矩阵的列向量满足一定的线性独立性；(2)测量矩阵的列向量体现某种类似噪声的独立随机性；(3)满足稀疏度的解是满足1-范数最小的向量。这3个特征对测量矩阵的构造起着重要的指导作用。

测量矩阵就确定性方面可以分为随机测量矩阵和确定性测量矩阵。随机测量矩阵的每一个元素都是独立同分布的，保证了测量矩阵列与列之间的不相关性，较好的满足了上述3个特征，因此对测量信号具有普遍适用性，而且用较少的采样便可获得较精确的重构。同时，正是由于随机矩阵每一个元素都独立地服从同一分布，之间没有任何的相关性和结构性，使得每一个元素都要存储，耗费大量的存储空间，不利于硬件实现。确定性测量矩阵的元素的位置和值都是确定的，易于硬件电路实现，但是对上述3个特征的符合度不如随机测量矩阵，因此在普适性和重构能力上一般次于随机测量矩阵。尽管随机测量矩阵的重构性能较为理想，但是出于对硬件电路实现问题的解决，对确定性测量矩阵的研究尤为必要。

3 分块的有序范德蒙矩阵

本文以第2.2节中提到的测量矩阵需要满足的3个特征为出发点，并且注意到自然图像在频域的稀疏系数集中分布在低频段的性质[12]，通过分析范德蒙矩阵，利用有效的方法将其改造为易于硬件实现且重构精度较高的测量矩阵。

3.1 范德蒙矩阵

范德蒙矩阵是一个各列或各行呈现出几何级数关系的矩阵，例如，式(5)的矩阵V就是一个m×n大小的范德蒙矩阵：

范德蒙矩阵有一个良好的性质，即，当ai(i= 1,2,…,n)互不相等时，从矩阵V中任意选取的k(k≤min(m,n ))个列向量或者行向量都是线性无关的[13]。这与文献[2]提出的测量矩阵应具有的第(1)个特征相符，即，测量矩阵的列向量满足一定的线性独立性。

3.2 分块的范德蒙矩阵

一般自然图像信号的行列维数都比较高，可以达到102～103的数量级或者更高，即便采用分块扫描或者逐列扫描方式采样，直接使用范德蒙矩阵V进行测量，行数m和列数n也都将在102～103的数量级，相对于ai(i=1,2,…,n)来说将会是非常大(当ai＞1)或者非常小(当ai＜1)的数值，这样用硬件实现起来将会非常困难；如果尽量使ai接近于1，使/ai不至于太大或者太小，那么会造成ai≈aj(i,j=1,2,…,n,i≠j )，这样列向量之间的非相关性就会减弱，从而降低信号的重构精度。因此将范德蒙矩阵直接用作测量矩阵并不是一个可取的办法，应该采取其他手段对范德蒙矩阵进行改进，使其易于硬件实现，同时列向量之间的非相关性不至于降低。

由上面的分析可知，范德蒙矩阵V的行数m和列数n应该取很小的值，这样易于硬件实现，同时ai(i=1,2,…,n)之间不能太接近，以确保列向量之间较强的非相关性。结合这两点，本文采用分块的方法对范德蒙矩阵进行改进，使范德蒙矩阵作为测量矩阵的子块(子矩阵)，对角排列成一个维数较大的测量矩阵，并称该测量矩阵为分块的范德蒙矩阵。对一个m×n的范德蒙矩阵V，对角排列成M×N的分块的范德蒙矩阵ΦB，而ΦB的非对角子矩阵全为零矩阵，即：

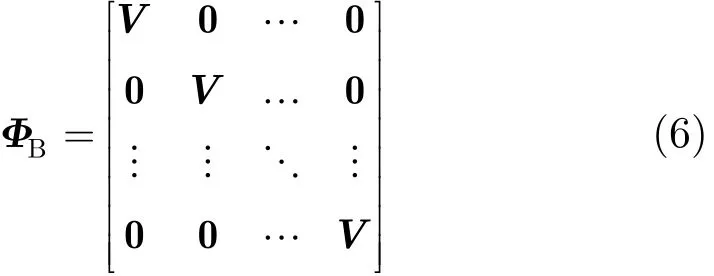
其中M/m=N/n=L 为块数。这样构造的测量矩阵使得范德蒙矩阵V的行数m和列数n都可以是非常小的整数，同时也可以使ai(i=1,2,…,n)之间的取值有一定差距，保证了列向量之间较强的非相关性。

3.3 分块的有序范德蒙矩阵

如果分块的范德蒙矩阵ΦB中子矩阵V的元素ai(i=1,2,…,n −1)满足ai＜ai+1，本文称这种分块的范德蒙矩阵为分块的有序范德蒙矩阵ΦBO。这种元素的有序排列可以保证自然图像信号进行稀疏分解时稀疏基和稀疏系数的对应结构性，在时域采样时实现非均匀采样，加强对低频段的采样，提高信号的重构精度。需要强调的是文献[12]和文献[14]的非均匀采样需要把信号变换到变换域后实现，而分块的有序范德蒙矩阵的非均匀采样可以直接在时域采样中实现。

由上述测量矩阵ΦBO的构造过程，可以发现对ΦBO分的块越小越利于硬件实现。不仅如此，在信号采样时，块越小计算复杂度越低。因为稠密矩阵在采样时需要进行MN次乘法运算，M(N−1)次加法运算，分块的有序范德蒙矩阵只需要Mn次乘法和M(n−1)次加法运算，而n比N要小得多。但是这并不意味着分的块越小越好，块越小往往会导致重构的精度越低，这是因为块越小零元素越多，采样时得到的信息量一般就越少。因此在实际问题中需要对块的大小和重构精度进行折中考虑。同时，本文还可以发现，稠密矩阵与分块的有序范德蒙矩阵在采样时的总体计算复杂度之比约为N/n，当信号维数N越大时(n固定不变)，比值N/n越大，这说明分块的有序范德蒙矩阵相比稠密矩阵更利于采样维数较高的信号。

通过上述分析，本文可以得到分块的有序范德蒙矩阵具有以下优点：分块方法的采用使矩阵产生了大量的零元素，而且ai(i=1,2,…,n)可以取整数，使得测量矩阵易于硬件实现；ai(i=1,2,…,n)的取值不同，使列向量之间有较强的非相关性，保证了信号的较高重构精度；矩阵元素有序性的排列实现了时域中的非均匀采样，加强了低频段的采样，进一步提高了对信号的重构精度；不同块的列向量之间非零元素的位置是不重叠的，采样的信号段也会不同，因此可以进行并行采样，减少采样时间；相对于稠密矩阵，分块的测量矩阵降低了信号采样时的计算复杂度，更利于采样维数较高的信号；测量矩阵的生成并没有复杂的运算，只有幂乘和复制操作，因此生成时间也非常短；分块和对角排列使测量矩阵具有很强的结构性，对M×N大小的测量矩阵ΦBO只需存储m×n 的范德蒙矩阵V和块数L，极大地减少了存储空间。进一步，根据有序性，可以使ai(i=1,2,…,n)为等差数列，这时只需存储初始值a1、公差d、子块的行数m、子块的列数n以及块数L这几个数值就可以生成整个矩阵。因此，这样构造的测量矩阵对硬件是极其友好的，而且有利于自然图像信号重构。

4 仿真与分析

本文采用2维图像信号进行仿真实验，对分块的有序范德蒙矩阵的重构性能进行了验证，作为对比实验的测量矩阵有常用的高斯随机矩阵、确定性测量矩阵中的基于混沌序列的测量矩阵以及结构性测量矩阵中常用的托普利兹矩阵。同时，为了验证元素的有序性排列实现了非均匀采样并且提高了信号的重构精度，本文加入了对元素无序排列的分块的范德蒙矩阵的比较。本文所有实验都是在Matlab2012a下进行的，使用的是3.00 GHz的双核台式计算机。稀疏基Ψ采用DCT基，重构算法采用SL0算法[16]。首先，分别对大小为256×256的Lena, Peppers, Cameraman和Boats图像在时域中进行了采样并重构。为了便于实验，本文对2维图像进行逐列采样和重构，因此各测量矩阵Φ的列数N=256。当采样率R=M/N=0.5时各测量矩阵对图像重构的结果如表1所示。

表1中分块的有序范德蒙矩阵的子矩阵V大小为4×8, ai采用等差序列，初值a1=1，公差d=1；分块的范德蒙矩阵是对分块的有序范德蒙矩阵进行随机乱序后得到的，由于随机性因素的存在，由它和高斯随机矩阵以及托普利兹矩阵所得到的结果都是在重复进行1000次实验后求得的平均值，下面的实验也如此处理。

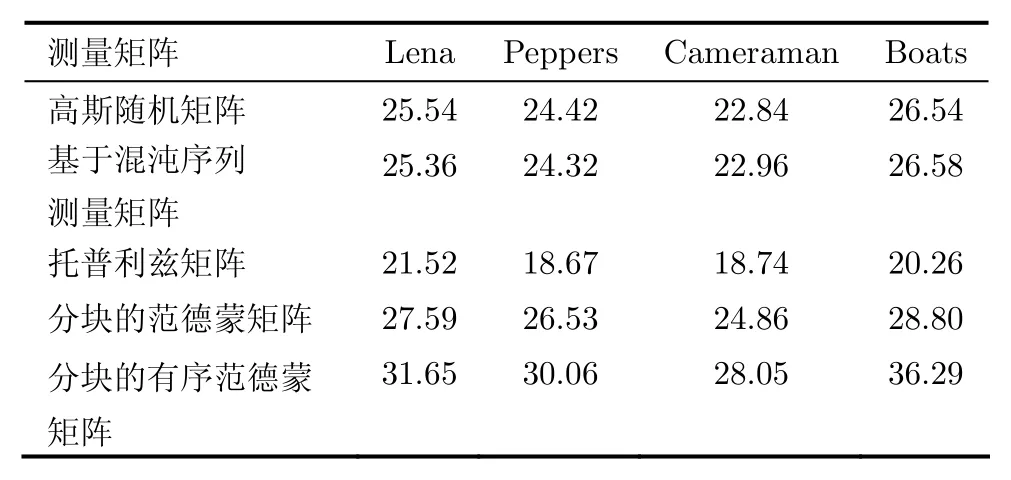
表1 采样率为0.5时，各测量矩阵对图像重构PSNR(dB)的比较

由表1可以看出，高斯随机矩阵和基于混沌序列测量矩阵对信号重构的PSNR比较接近，托普利兹矩阵的重构精度最低；分块的范德蒙矩阵对信号的重构精度高于上述3个测量矩阵，说明矩阵列向量的非相关性有利于信号重构；分块的有序范德蒙矩阵的重构精度比分块的范德蒙矩阵有进一步的提升，说明元素的有序性排列起了作用，但是还无法说明它实现了非均匀采样。

为了便于从视觉角度上进行比较，图1列出了上述实验各测量矩阵对Lena图像重构后的效果图，从视觉角度看，分块的有序范德蒙矩阵也远远优于其他测量矩阵。

为了进一步验证本文提出的测量矩阵相比其它测量矩阵在重构精度上具有明显优势，本文在不同的采样率下，用上述测量矩阵对Lena图像在时域进行了采样并重构，重构结果如图2所示(在不同采样率下的分块的有序范德蒙矩阵按以下方式取得：采样率为0.1～0.8时，子块V的行m固定为4，采样率为0.9时，m固定为9；列n根据采样率取大于等于mN/M的最小整数，对得到的整个矩阵取前M行和前N列即为测量矩阵。分块的范德蒙矩阵是在对应采样率的分块的有序范德蒙矩阵的基础上进行随机乱序得到的)。由图2结果可见，分块的有序范德蒙矩阵在任何采样率下都优于其它测量矩阵。

图1 各测量矩阵对Lena图像重构效果比较

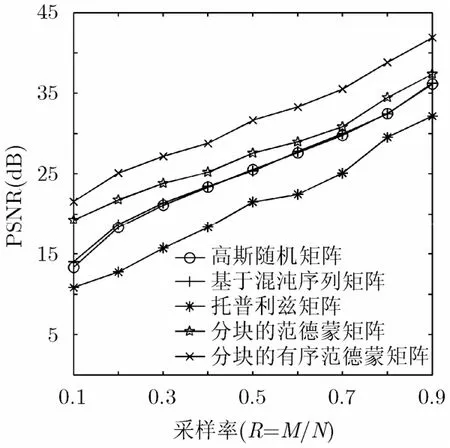
图2 各测量矩阵对Lena图像在不同采样率下重构结果比较

上述实验，从分块的有序范德蒙矩阵和分块的范德蒙矩阵的对比中可以看出，元素的有序性排列的确提高了信号的重构精度，但是还不能说明分块的有序范德蒙矩阵实现了非均匀采样。为了验证其实现了非均匀采样，加强了对低频部分的采样，本文进行了如下实验：用不同的测量矩阵在采样率R=0.5下分别对Lena图像在时域进行采样并重构，然后再分别比较重构图像的高频部分和低频部分的相对误差。相对误差公式为100%，其中fr表示重构图像的DCT系数，fo表示原始图像的DCT系数，计算高频部分相对误差时，fr, fo采用高频部分DCT系数，计算低频部分相对误差时，fr, fo采用低频部分DCT系数(不包含直流系数)，计算总的相对误差时，fr, fo采用全部DCT系数。实验结果如表2所示。

由表2可以看出，高频部分，除分块的有序范德蒙矩阵的相对误差相对较大外，其余测量矩阵的相对误差比较接近；而低频部分，各个测量矩阵的相对误差差距较大。这是因为图像信号低频系数数值较大，容易重构，而高频系数较小且普遍接近于零，不易精确重构，所以各个测量矩阵重构误差主要体现在低频部分。分块的有序范德蒙矩阵和分块的范德蒙矩阵只有元素排列顺序的差别，从两者对Lena图像高低频相对误差的差距中可以看出，分块的有序范德蒙矩阵加强了对低频部分的采样，使得低频部分的重构误差有较大幅度的降低，高频部分的重构误差有一定增加，又由于该实验是在时域中进行的，这说明分块的有序范德蒙矩阵在时域中实现了非均匀采样。通过表2中的总的相对误差可以看出，这种非均匀采样从整体上提高了测量矩阵对图像的重构精度。

考虑到块大小对实际应用有着重要的影响作用，本文还对不同块大小情况下的分块的有序范德蒙矩阵进行了实验。在采样率R=0.5以及块大小分别为3×6, 4×8, 5×10和6×12的情况下，分别对大小为256×256的Lena, Peppers, Cameraman和Boats图像在时域中进行了采样并重构，重构效果如表3所示。

通过表3的纵向比较，可以得出分的块越大，图像的重构精度越高，这和第3.3节中的分析是一致的。但是随着分块大小的逐渐变大，重构精度的提升也越来越小，这主要是因为子矩阵中an和an−1的相对差距越来越小(即越来越小)，导致了相应列的非相关性降低。同时，还应注意到，并不是分块越大越好，分块越大反而增加了硬件电路实现的难度(太大的块也毫无实际意义，因为指数增长太快了，硬件难以实现)，也增加了采样时的计算复杂度。所以，在实际的应用情况中，应有一个折衷的考虑。

表2 采样率为0.5时，各测量矩阵重构Lena图像的高、低频相对误差(%)

表3 分块的有序范德蒙矩阵在不同块大小情况下对各图像重构PSNR(dB)的比较

5 结束语

本文提出了一种新的确定性测量矩阵，即分块的有序范德蒙矩阵。范德蒙矩阵具有线性不相关的优良性质，但是其元素呈现出的几何级数关系限制了其直接作为测量矩阵的使用。本文采用分块的技术，将其改造为矩阵元素可以是整数且极其稀疏的矩阵，同时还保留了向量线性不相关的性质。注意到自然图像在频域的稀疏系数集中分布在低频段的特点，本文又将范德蒙矩阵的元素进行了有序排列，实现了时域的非均匀采样。大量实验表明，通过分块和排序得到的分块的有序范德蒙矩阵对2维图像信号的重构精度远远高于高斯随机矩阵等。同时，该矩阵还具有构造简单、占用存储空间少和计算复杂度低等优点。因此，分块的有序范德蒙矩阵是一种极易于硬件实现且重构精度较高的测量矩阵。

[1] Candes E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[2] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[3] Donoho D L and Tsaig Y. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 533-548.

[4] Duarte M F, Davenport M A, Takhar D, et al.. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 83-91.

[5] DeVore R. Deterministic constructions of compressed sensing matrices[J]. Journal of Complexity, 2007, 23(46): 918-925.

[6] 林斌, 彭玉楼. 基于混沌序列的压缩感知测量矩阵构造算法[J]. 计算机工程与应用, 2013, 49(23): 199-202.

Lin Bin and Peng Yu-lou. Measurement matrix construction algorithm for compressed sensing based on chaos sequence[J]. Computer Engineering and Applications, 2013, 49(23): 199-202.

[7] Mohades M M, Mohades A, and Tadaion A. A reed-solomon code based measurement matrix with small coherence[J]. IEEE Signal Processing Letters, 2014, 21(7): 839-843.

[8] Liu Xin-ji and Xia Shu-tao. Constructions of quasi-cyclic measurement matrices based on array codes[C]. Proceedings of the IEEE International Symposium on Information Theory, Istanbul, Turkey, 2013: 479-483.

[9] Gan L. Block compressed sensing of natural images[C]. 15th IEEE International Conference on Digital Signal Processing, Cardiff, Wales, 2007: 403-406.

[10] 张波, 刘郁林, 王开. 稀疏随机矩阵有限等距性质分析[J]. 电子与信息学报, 2014, 36(1): 169-174.

Zhang Bo, Liu Yu-lin, and Wang Kai. Restricted isometry property analysis for sparse random matrices[J]. Journal of Electronics & Information Technology, 2014, 36(1): 169-174.

[11] Bajwa W U, Haupt J, Raz G, et al.. Toeplitz-structured compressed sensing matrices[C]. Proceedings of the IEEE Workshop on Statistical Signal Processing (SSP), Madison, USA, 2007: 294-298.

[12] Zhao Rui-zhen, Li Hao, Qin Zhou, et al.. A new construction method for generalized Hadamard matrix in compressive sensing[C]. Proceedings of the 2011 Cross-Strait Conference on Information Science and Technology, Danshui, China, 2011: 309-313.

[13] 居余马. 线性代数[M]. 第2版, 北京: 清华大学出版社, 2002: 17-18.

Ju Yu-ma. Linear Algebra[M]. 2nd Edition, Beijing: Tsinghua University Press, 2002: 17-18.

[14] Jalbin J, Hemalatha R, and Radha S. Two measurement matrix based nonuniform sampling for wireless sensor networks[C]. Proceedings of the 3rd International Conference on Computing Communication & Networking Technologies (ICCCNT'2012), Coimbatore, India, 2012: 1-4.

[15] 李珅, 马彩文, 李艳, 等. 压缩感知重构算法综述[J]. 红外与激光工程, 2013, 42(S1): 225-232.

Li Kun, Ma Cai-wen, Li Yan, et al.. Survey on reconstruction algorithm based on compressive sensing[J]. Infrared and Laser Engineering, 2013, 42(S1): 225-232.

[16] Mohimani H, Babaie-Zadeh M, and Jutten C. A fast approach for overcomplete sparse decomposition based on smoothed l0norm[J]. IEEE Transactions on Signal Processing, 2009, 57(1): 289-301.

赵瑞珍： 男，1975年生，博士，教授，研究方向为图像处理、小波变换、压缩感知等.

王若乾： 男，1986年生，硕士生，研究方向为压缩感知测量矩阵构造与优化.

张凤珍： 女，1983年生，博士生，研究方向为压缩感知及其应用.

Research on the Blocked Ordered Vandermonde Matrix Used as Measurement Matrix for Compressed Sensing

Zhao Rui-zhen Wang Ruo-qian Zhang Feng-zhen Cen Yi-gang Hu Shao-hai
(Institute of Information Science, Beijing Jiaotong University, Beijing 100044, China)
(Key Laboratory of Advanced Information Science and Network Technology of Beijing, Beijing 100044, China)

The measurement matrix is an important part of Compressed Sensing (CS). Although the deterministic matrix is easy to implement by the hardware, it performs not so well as a random matrix in the signal reconstruction. To solve this problem, a new deterministic measurement matrix which is called as the blocked ordered Vandermonde matrix is proposed. The blocked ordered Vandermonde matrix is constructed on the basis of the Vandermonde matrix, whose the vectors are linearly independent. Then the block operation is taken and its elements are sorted. The proposed new measurement matrix realizes the non-uniform sampling in the time domain and is specifically suitable for the natural images whose the dimension is usually high. The simulation results show that the proposed matrix is much superior to the Gaussian matrix in the image construction, and can be used in practice.

Compressed Sensing (CS); Measurement matrix; Linear independence; Non-uniform sampling; Vandermonde matrix

TN911.7

：A

：1009-5896(2015)06-1317-06

10.11999/JEIT140860