分布式目标的极化SAR距离模糊计算方法研究

洪 文杨士林*③李 洋③张晶晶③郭胜龙③

①(微波成像技术国家级重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院大学 北京 100190)

分布式目标的极化SAR距离模糊计算方法研究

洪 文①②杨士林*①②③李 洋①②③张晶晶①②③郭胜龙①②③

①(微波成像技术国家级重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院大学 北京 100190)

该文提出了一种运用协方差矩阵计算星载全极化SAR距离模糊的方法。首先分析了极化SAR距离模糊的成因及同极化和交叉极化通道间距离模糊能量的差异。现有的距离模糊计算方法以散射矩阵为主，受相干斑影响，单一像素的散射强度不能表征分布目标的反射率，因而在距离向相邻的像素无法确定其距离模糊比。针对上述问题该文推导了基于分布目标的极化SAR距离模糊的计算方法。结合Radarsat-2实测数据对这种新方法进行了验证。实验表明，运用协方差矩阵能够很好地表征分布式目标，由它计算得出的距离模糊比是平稳、确定的。相比已有算法，所提方法能够有效计算极化SAR分布式目标的距离模糊。

合成孔径雷达；分布目标；极化SAR；距离模糊

1 引言

合成孔径雷达(SAR)是一种全天时、全天候的高分辨率成像雷达。雷达天线主瓣照射的区域为测绘带。距离模糊是由于天线主瓣以外的旁瓣回波信号与所需测绘带内信号回波同时到达天线所造成的。距离模糊对于宽测绘带SAR系统的参数设计起着非常重要的作用，它是影响SAR成像的一个重要因素[1]。目前单极化SAR系统的距离模糊分析已有很多详细的讨论[2−4]，而多极化SAR距离模糊的计算研究相对较少，该文主要分析了星载全极化SAR系统的距离模糊及其详细计算方法。目前的极化SAR系统距离模糊计算中[5−7]，用表征地面散射特性的极化散射矩阵来直接计算距离模糊并不妥当。这是因为：星载SAR目标是分布式目标，它们随环境和时间而动态变化。受相干斑影响[8]，相邻像素间的信号强度是不连续的，如果从散射矩阵出发分析距离模糊比，那么计算出的交叉极化功率仍在扰动，就无法判断同极化和交叉极化功率的相对大小，从而出现相邻像素距离模糊比不能确定的问题。另外，交叉极化能量较同极化能量低6～10 dB[9]，但不能直接体现在散射矩阵上。对于星载SAR目标来说，极化数据的二阶统计量协方差矩阵是大量分辨单元平均后的结果，它是稳定的。用协方差矩阵来参与计算距离模糊是合理的，并且可以表征交叉极化能量和同极化能量的关系。该文首先分析了极化SAR距离模糊的形成原因，并且分析了同极化和交叉极化通道模糊能量的差异；详细推导了基于分布式目标的极化SAR距离模糊的计算方法。接着结合数据对这种新方法进行了仿真验证。最后与现有的计算距离模糊的方法进行了对比分析。

2 极化SAR距离模糊分析与计算

2.1 距离模糊分析

极化SAR系统的工作模式为交替发射水平(H)、垂直(V)极化波。在发射脉冲间隔内同时接收发射脉冲对应的H, V散射回波。如图1所示，发射H极化波时，水平通道接收HH散射波，垂直通道接收HV散射波；发射V极化波时，水平通道接收VH 散射波，垂直通道接收VV散射波。工作时序如图1所示。

图1 极化SAR工作时序图(交叉极化回波比同极化回波低6～10 dB)

在距离向，假设某一区域的回波延时和观测带内目标的回波延时正好相差整数倍个脉冲周期，这就形成了距离模糊，产生模糊信号的那个区域称为距离模糊区，或者与观测处的斜距相差整数个脉冲数的区域即为模糊区[10−12]。对于这种交替发射，同时接收的极化SAR工作模式，某个回波接收时刻，接收信号除了感兴趣的信号之外，也有正好相差整数j个脉冲重复周期(IPP)的模糊回波信号。当j为奇数时，模糊回波信号对应的发射脉冲和有用信号对应的发射脉冲极化方式相反。我们把对应的模糊区为称奇数模糊区(odd ambiguity zones)。当j为偶数时，模糊回波信号对应的发射脉冲和有用信号对应的发射脉冲极化方式相同。我们把对应的模糊区称作偶数模糊区(even ambiguity zones)。图2所示是极化SAR距离模糊示意图。与t=0时刻相差Tp(脉冲重复周期)，−Tp的发射脉冲与t=0时刻的发射脉冲极化方式相反，对应的模糊区域为奇数模糊区。与t=0时刻相差2Tp,−2Tp的发射脉冲与t=0时刻的发射脉冲极化方式相同，对应的模糊区域为偶数模糊区。

基于以上分析，由文献[9]可知，极化SAR观测散射矩阵为

式中，RAR表示距离模糊比。等号右边第1项表示测绘带(swath)内感兴趣目标的散射矩阵，剩余两项为距离模糊区域散射矩阵，j=od 为奇数模糊区域，j=ev为偶数模糊区域。

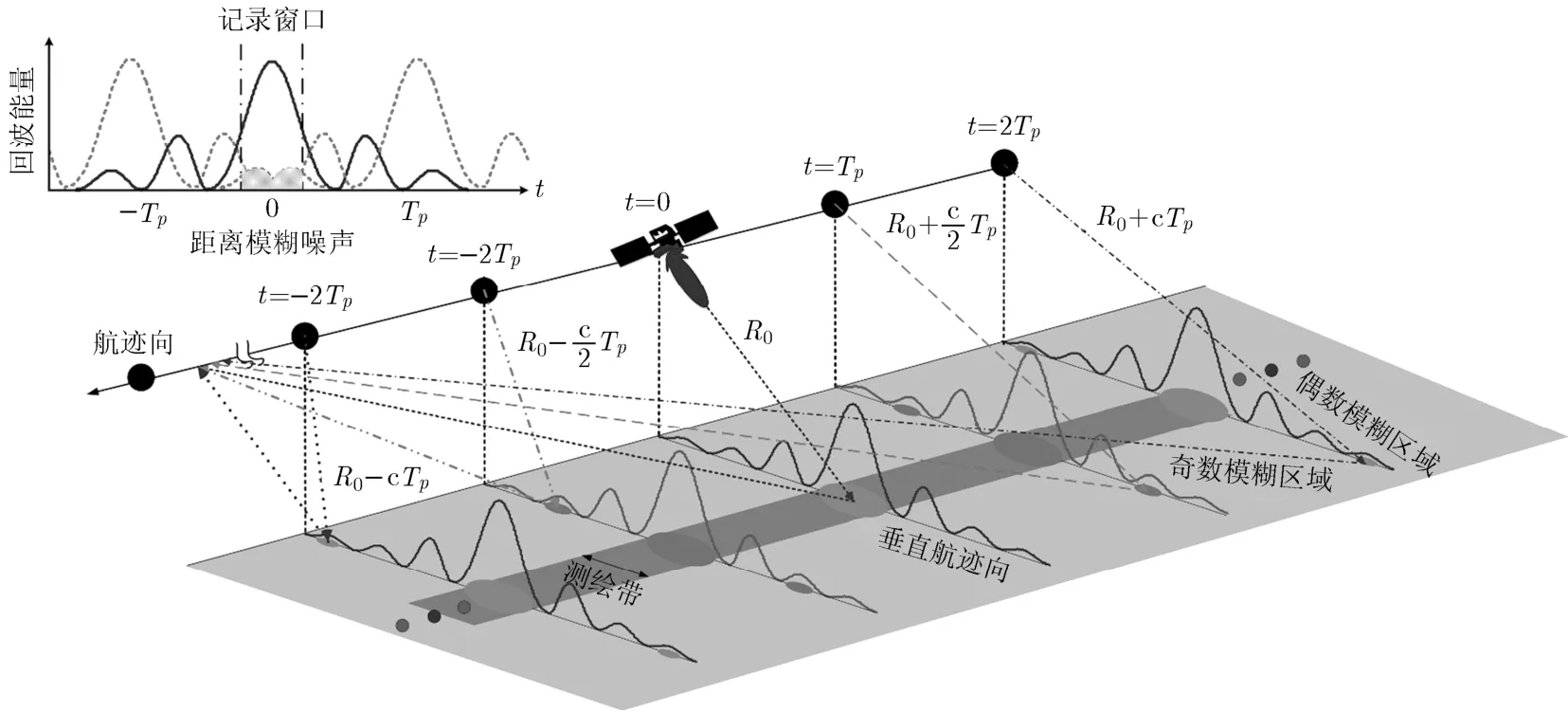
图2 极化SAR距离模糊示意图

由式(1)看出，有用信号同极化通道模糊能量分别来自奇数模糊区交叉极化通道和偶数模糊区同极化通道；有用信号交叉极化通道模糊能量分别来自奇数模糊区同极化通道和偶数模糊区交叉极化通道。由于同极化通道能量比交叉极化通道能量高6～10 dB，因此交叉极化通道受来自奇数模糊区同极化模糊能量的主导，模糊比值比较大[13]。

2.2 分布式目标距离模糊计算推导

下面推导距离模糊的计算公式。雷达信号接收电压表达式为

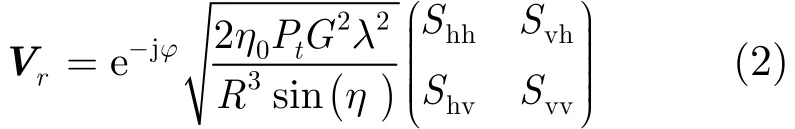
其中ϕ=−2kR ,R是散射目标到天线的斜距， η0=μ0和ε0分别表示磁导率和电导率，η是本地入射角，Pt是天线发射功率，G表示天线增益，λ是波长。

那么根据式(1)可以得到极化SAR的接收电压为

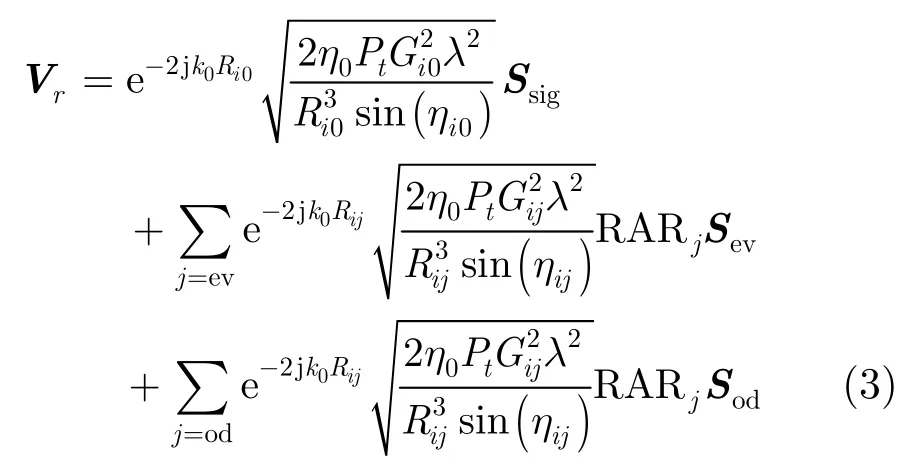
其中Ssig,Sev,Sod分别表示有用信号，偶数模糊区，奇数模糊区的散射矩阵。

由于星载SAR目标是随环境动态变化的，因此可以假设有用信号与模糊信号不相关，模糊信号之间也不相关(上标H表示共轭转置)，即

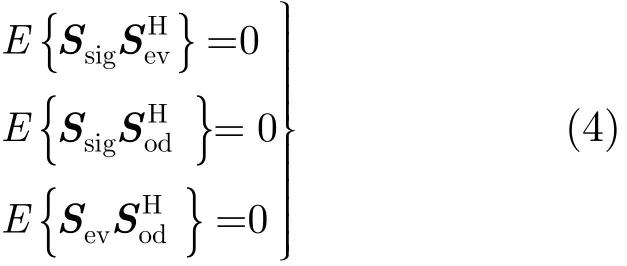
那么接收信号功率可以表示为

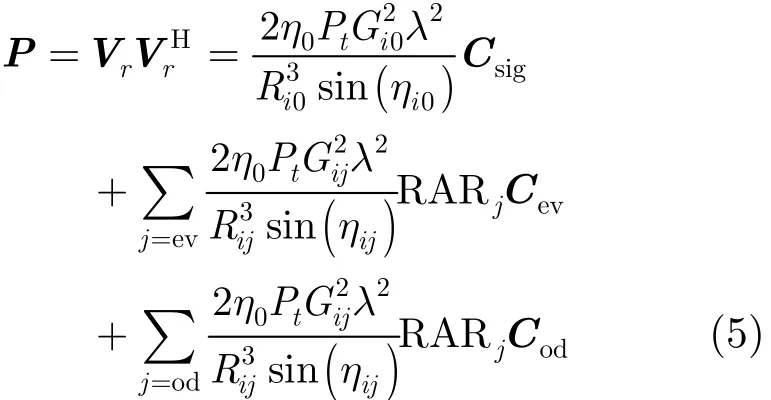
其中，C=SSH是协方差矩阵。j是模糊区标号，其中j=0表示测绘带内感兴趣的脉冲。i是测绘带内采样点标号，Ri0表示观测带内的第i个采样点对应的斜距。那么Rij表示给i点造成模糊的所有点的斜距值。由式(6)就可以计算得出整数j的值。

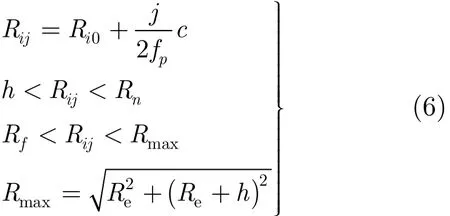
Rn和Rf分别表示测绘带内的近点斜距和远点斜距值；Re和h分别表示地球半径和轨道高度。图3表示斜距几何关系。

图3中，SAR到地球中心的距离定义为Rs=Re+h,γij为对应于入射角ηij的天线视轴角。

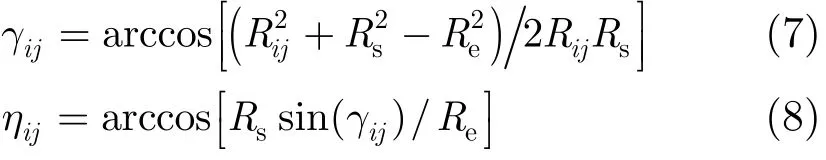
Gij表示在给定的γij下的天线方向图。对于均匀照明孔径，远场方向图由式(9)定义：

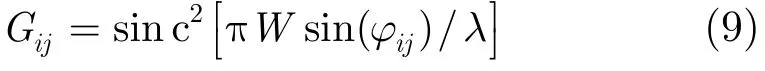
其中离轴高度角计算式为

式中，γ0表示天线下视角(look angle), r表示横滚角。

根据距离模糊比(RASR)的定义[14]，距离模糊比是模糊信号能量与有用信号能量的比值，即

图3 斜距几何关系图

根据式(1)和式(11)，传统极化HH通道距离模糊比为

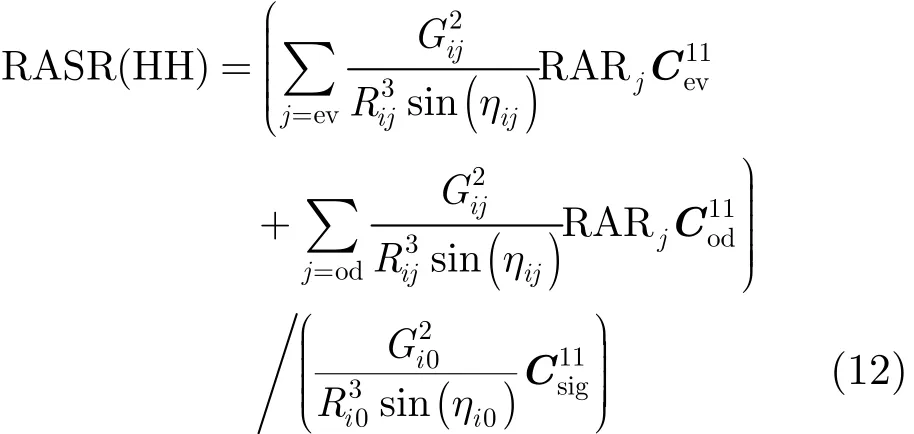
同理，传统极化HV通道距离模糊比为

其中Cmn表示C协方差矩阵第m行，第n列的元素。由式(1)可知，极化SAR系统中C项是同极化通道，C和C是模糊能量中给同极化通道造成模糊的项。

至此，已详细给出由全极化协方差矩阵C推导出距离模糊的计算表达式。下面用Radarsat-2实测数据进行验证与分析。

3 实验结果

3.1 实验数据介绍

实验所用实测数据来自于Radarsat-2系统，系统主要参数如表1所示。

文章分别对旧金山地区分布式目标海洋和森林运用本文的方法进行了计算。

3.2 实验结果与分析

根据文献[6]现有的计算全极化SAR距离模糊的方法，海洋和森林的距离模糊计算结果如图4～图7所示。

由图4～图7可以看出，用散射矩阵描述分布式观测对象，无论是海洋还是森林，每条距离模糊比曲线变化很不稳定，曲线中相邻两点的距离模糊比跳变很大，而且如果存在强散射点，距离模糊比甚至有超过0 dB的可能。这是由于在距离模糊计算中，受相干斑因素的影响，相邻像素的信号强度是不连续的，单一像素的极化散射矩阵不能表征分布式目标的散射率，由散射矩阵计算得出极化功率时刻在随时间和空间而扰动[15]。极化数据的二阶统计量协方差矩阵是稳定的，是大量分辨单元平均后的结果，因此本文的运用散射数据的二阶量协方差矩阵计算距离模糊是合理的。图8～图11结果是依据本文方法对海洋和森林目标计算得到的。

表1 Radarsat-2系统参数

图8～图11是采用本文的方法计算距离模糊比。由图可以看出距离模糊比曲线比较平缓光滑，计算结果是比较稳定的，所以可以根据当前某点的距离模糊比值而推理得到与它相邻点的距离模糊比值以及变化趋势。

此外，图8所示是同极化通道的距离模糊比值，图中测绘带内大部分区域距离模糊比都低于-20 dB(一般要求距离模糊比低于-20 dB)。图9所示的交叉极化通道低于-20 dB的测绘带宽不到20 km。这是因为由式(1)可知HV, VH有用回波信号的模糊能量受同极化信号的主导，因为同极化回波能量要比交叉极化高6～10 dB，所以交叉极化通道的距离模糊严重一些。HH, VV同极化波在奇数模糊区受交叉极化波的影响，因此它们所受的影响较小。偶数模糊区域和单极化SAR系统的模糊一样。

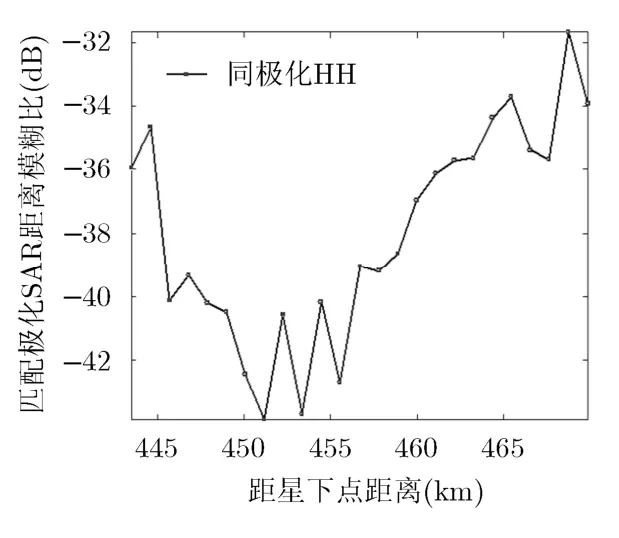
图4 海洋同极化通道距离模糊比

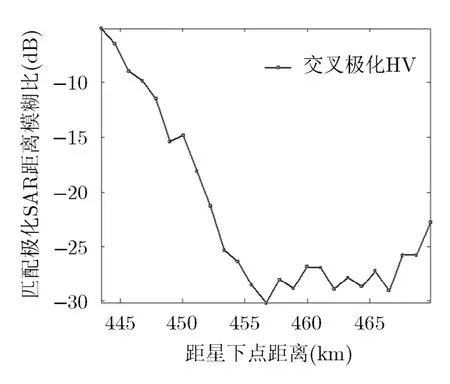
图5 海洋交叉极化通道距离模糊比

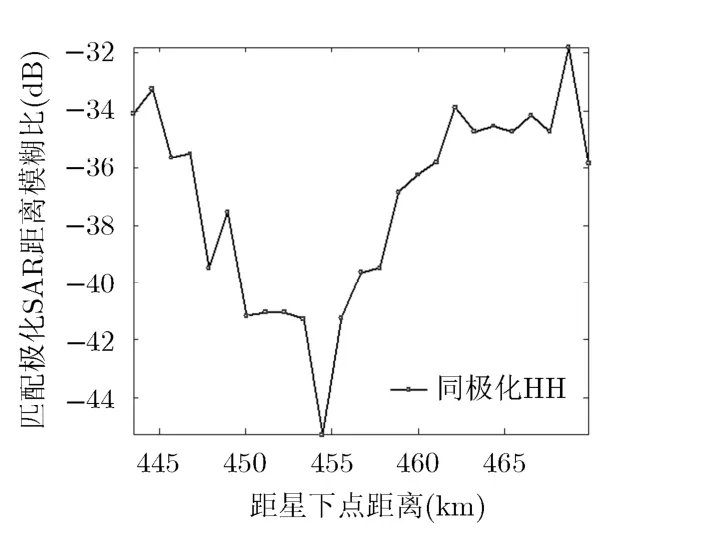
图6 森林同极化通道距离模糊比

图7 森林交叉极化通道距离模糊比

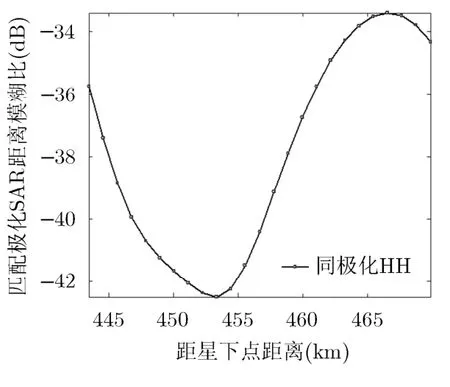
图8 海洋同极化通道距离模糊比

图9 海洋交叉极化通道距离模糊比

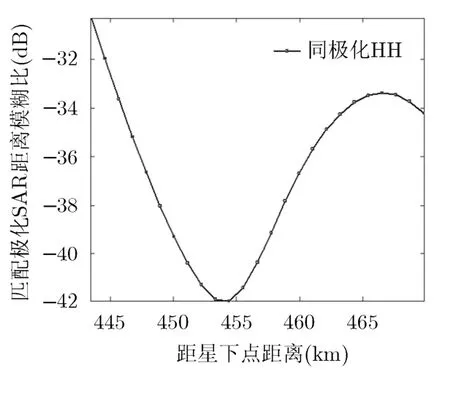
图10 森林同极化通道距离模糊比

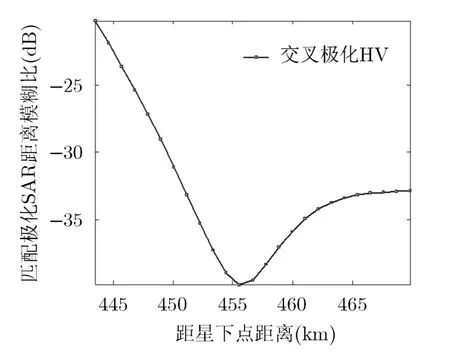
图11 森林交叉极化通道距离模糊比

4 结束语

本文详细地分析了极化SAR系统距离模糊形成的原因，针对现有的星载极化SAR距离模糊计算方法中用散射矩阵无法描述分布式观测对象极化散射特征的问题，本文提出了一种运用协方差矩阵计算星载全极化SAR距离模糊的方法。详细推导出极化SAR系统HH, HV通道距离模糊的计算公式。最后，通过Radarsat-2旧金山地区海洋和森林分布式目标距离模糊计算，验证了运用协方差矩阵计算极化SAR系统距离模糊的合理性与精确性，为极化SAR距离模糊分析与计算提供一种有价值的参考。

[1] 韩晓东, 宋红军, 徐伟. 基于星载SAR实时波束形成的星下点及距离模糊抑制方法[J]. 电子与信息学报, 2013, 35(12): 2821-2828.

Han Xiao-dong, Song Hong-jun, and Xu Wei. Nadir and range ambiguity suppression based on real-time digital beam froming in spaceborne SAR[J]. Journal of Electronics & Information Technology, 2013, 35(12): 2821-2828.

[2] Wang Wen-qin. Mitigating range ambiguities in high-PRF SAR with OFDM waveform diversity[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 101-105.

[3] Yang Jun, Sun Guang-cai, Wu Yu-feng, et al.. Range ambiguity suppression by azimuth phase coding in multichannel SAR systems[C]. IET International Radar Conference 2013, Xi'an, China, 2013: 1-5.

[4] Davis Michael S and Cook Daniel A. Quantifying the impact of range and azimuth ambiguities on multichannel SAR and SAS image quality[C]. EUSAR 2014: 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1-4.

[5] Ralph C and Pierluigi M. Range ambiguities for a polarimetric spaceborne SAR[C]. IGARSS 92: Proceedings of the 12th Annual International Geoscience and Remote Sensing Symposium, Houston, TX, US, 1992: 637-639.

[6] 李延, 丁泽刚, 郭佳佳. 多极化星载SAR模糊比分析与计算[J]. 航天器工程, 2011, 20(1): 45-49.

Li Yan, Ding Ze-gang, and Guo Jia-jia. Ambiguity analysis and calculation of polarimetric SAR[J]. Spacecraft Engineering, 2011, 20(1): 45-49.

[7] 戴博伟, 杨汝良. 多极化星载合成孔径雷达系统新工作方式及模糊分析[J]. 电子与信息学报, 2001, 23(12): 1256-1263.

Dai Bo-wei and Yang Ru-liang. New operation modes and ambiguity analysis for spaceborne polarimetric SAR system [J]. Journal of Electronics & Information Technology, 2001, 23(12): 1256-1263.

[8] Foucher S and Lopez-Martinez C. Analysis, evaluation, and comparison of polarimetric SAR speckle filtering techniques [J]. IEEE Transactions on Image Processing, 2014, 23(4): 1751-1764.

[9] Raney R K, Freeman A, and Jordan R L. Improved range ambiguity performance in quad-pol SAR[J]. IEEETransactions on Geoscience and Remote Sensing, 2012, 50(2): 349-356.

[10] 刘军鹰, 蔡竟业, 王文钦. 星载距离向多波束SAR的系统模糊特性[J]. 信息与电子工程, 2012, 10(2): 138-142.

Liu Jun-ying, Cai Jing-ye, and Wang Wen-qin. Ambiguity characteristics of spaceborne range multi-beam SAR systems[J]. Information and Electronic Engineering, 2012, 10(2): 138-142.

[11] 席龙梅, 盛磊, 葛家龙. 星载滑动聚束SAR模糊特性分析与仿真[J]. 上海航天, 2011, 28(1): 1-6.

Xi Long-mei, Sheng Lei, and Ge Jia-long. Analysis and simulation of ambiguities on spaceborne sliding spotlight SAR[J]. Aerospace Shanghai, 2011, 28(1): 1-6.

[12] 荆麟角. 星载SAR距离模糊分布规律及其改进设计[J]. 电子科学学刊, 1994, 16(5): 490-496.

Jing lin-jiao. Range ambiguity distribution characteristic of spaceborne SAR and its design consideration[J]. Journal of Electronics, 1994, 16(5): 490-496.

[13] 陈祺, 黄海风, 余安喜, 等. 一种改善交叉极化距离模糊度的新工作模式[J]. 电波科学学报, 2013, 28(6): 1082-1087.

Chen Qi, Huang Hai-feng, Yu An-xi, et al.. A new working mode to improve the cross-polarization range ambiguity to signal ratio[J]. Chinese Journal of Radio Science, 2013, 28(6): 1082-1087.

[14] Curlander J C and McDonough R N. Synthetic Aperture Radar Systems and Signal Processing[M]. Wiley Series in Remote Sensing, Hoboken, NJ: Wiley, 1991: 303-306.

[15] Lee J S and Pottier E. Polarimetric Radar Imaging from Basic to Application[M]. Boca Raton, FL, Taylor & Francis Group, 2009: 74-75.

洪 文： 女，1968年生，研究员，博士生导师，研究方向为SAR成像与系统及其应用、极化/极化干涉SAR数据处理及应用、3维微波成像新概念新体制新方法等.

杨士林： 男，1989年生，硕士生，研究方向为混合极化SAR系统仿真.

李 洋： 男，1983年生，博士生，研究方向为极化SAR、简缩极化SAR、相干层析理论研究与应用.

张晶晶： 男，1986年生，博士生，研究方向为极化SAR、简缩极化SAR、极化定标理论研究.

郭胜龙： 男，1987年生，博士生，研究方向为极化SAR/简缩极化SAR理论研究与应用.

Study on Polarimetric SAR Range Ambiguity Computation for Distributed Targets

Hong Wen①②Yang Shi-lin①②③Li Yang①②③Zhang Jing-jing①②③Guo Sheng-long①②③

①(Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China)

②(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)

③(University of Chinese Academy of Sciences, Beijing 100190, China)

A new approach is proposed to compute spaceborne SAR range ambiguity using covariance matrix. The causation of range ambiguity of spaceborne SAR and the ambiguous energy difference between like-polarized channel and cross-polarized channel are analyzed. In current study, it is common to use polarimetric scattering matrix to compute range ambiguity. Because of the speckle, the scattering matrix of a pixel can not describe the distributed targets precisely. Therefore, it is hard to decide the range ambiguity signal ratio of adjacent pixels. In this paper, the formulation of computing range ambiguity is derived for distributed targets first. Second, this new method is tested by using Radarsat-2 data. The results show that covariance matrix can effectively illustrate distributed targets. The results are smooth and confirmed. The new method is rational to compute range ambiguity of distributed targets.

SAR; Distributed targets; Polarimetric SAR; Range ambiguity

TN958

： A

：1009-5896(2015)06-1437-06

10.11999/JEIT141234

2014-09-23收到，2015-02-13改回

*通信作者：杨士林 slyangcau@163.com