利用0-1矩阵分解集成的极化SAR图像分类

陈 博王 爽焦李成刘 芳毛莎莎张 爽

①(西安电子科技大学智能感知与图像理解教育部重点实验室 西安 710071)

②(西安电子科技大学计算机学院 西安 710071)

利用0-1矩阵分解集成的极化SAR图像分类

陈 博*①王 爽①焦李成①刘 芳②毛莎莎①张 爽①

①(西安电子科技大学智能感知与图像理解教育部重点实验室 西安 710071)

②(西安电子科技大学计算机学院 西安 710071)

全极化合成孔径雷达(PolSAR)图像蕴含更丰富的散射信息，具有更多的可用特征。如何使用这些特征是极化SAR图像分类中非常重要的一步，但是目前尚未对此提出非常明确的准则。为了能够有效地解决上述问题，该文提出一种基于特征加权集成的极化SAR图像分类算法。该算法采用0-1矩阵分解集成方法对包括不同特征的数据集进行学习获得相应加权系数，并通过对每个特征集获得的预测结果进行加权集成来提高极化SAR图像分类性能。首先，输入极化SAR数据，获得极化特征作为原始特征集，并对其进行随机抽取获得不同的特征子集；然后，使用0-1矩阵集成算法得到每个特征值相对应的加权系数；最后，通过对各个特征子集的预测结果进行集成得到最终极化SAR图像分类结果。实测L波段和C波段极化数据的实验结果表明，该算法可以有效地提高极化SAR图像分类的准确度。

极化合成孔径雷达；监督图像分类；集成学习；分类器集成

1 引言

近年来，极化合成孔径雷达(Polarimetric SAR, PolSAR)图像已经成为了一个非常热门的研究方向，而地物分类作为最重要的极化SAR图像研究方向之一，也受到了广泛的关注。和单极化SAR图像相比，其数据涵盖了地物目标散射特性，对回波信息进行了特定的分析和处理，从而提取了更为丰富的信息[1]。在国内外学者已经提出的众多经典分类方法当中，一类方法是基于测量到的数据，比如散射矩阵S，相干矩阵T，协方差矩阵C[2]和基于相干矩阵T特征值与特征向量分解的H/alpha方法[3]及相关研究改进[4,5]；另一类算法是基于目标散射理论，这些算法的核心是将数据分解成相互独立的成分，而每一部分都有其相对应的物理含义，如基于Freeman分解[6]的分类方法及改进[7,8]和Yamaguchi分解[9]及改进[10−12]；还有一类方法是用经典数据模型或者机器学习的方法对极化数据进行处理，如Wishart分类器[13]和支撑向量机(SVM)[14,15]。其中，前两类算法是基于散射回波信息和地物目标的散射特性给出的，因此可以得到一系列物理量能够有效地将极化SAR图像中的地物类型区别开，可以被用作其他分类方法中的特征值。这些特征值在给极化SAR图像分类研究带来丰富的地物散射信息的同时，也带来了一些困难。

通常在实际应用中，特征需要在分类过程进行之前被提取和进行处理。如何使用特征、使用哪些特征是图像分类分类器设计当中的关键步骤。而关于特征处理有两类主要算法：寻找特征子集和特征加权。特征加权是指给出一组特征的组合，通过相应的权值来控制其对最终分类结果的影响。但是，哪些特征可以得到更好的分类结果，却是很难预先确定下来的。目前，对于已有的特征处理算法而言，大多数算法都只是寻求唯一的一组特征组合来对所有的类别进行分类。然而，从某种程度上来讲，这样既会增加类别之间决定边界的复杂度[16]，又会限制到分类的准确性。此外，地物散射信息存在随机性，由于角度、形状、介电常数等多种因素，同一类别的像素却可能蕴含不同散射信息，而不同类别的像素可能存在相似的散射信息[17]。那么，每一个特征值的有效性将会受到不同的地物目标甚至是同一地物目标不同位置的影响，也就是说不同的特征对于不同的散射类型和地物目标有着不同的区分能力。如果要用单一的特征组合对所有的类别均有效，则必然要求大量的特征数据。

为了解决上述问题并更好发挥极化SAR图像特征的有效性，本文考虑用基于不同地物类别的多重特征组合代替之前提到的对于全图使用单一特征组合的方式来进行特征加权和图像分类。因此，提出了一种基于0-1矩阵分解加权集成框架下的极化SAR图像分类算法。在本文算法中，首先，根据经典算法所给出的多个特征组成初始特征集，并从中多次随机抽取若干特征组成多个特征子集；然后，基于获得的特征子集学习得到多个个体分类器；最后使用基于0-1矩阵分解的加权集成算法[18]将多个个体分类器的结果进行集成。实际上，本文通过将集成学习思想引入到极化SAR图像分类中，通过对每个特征子集对应的个体分类器加权来实现极化SAR图像特征加权的过程。对不同的类别或者对于同一类别不同位置的待测样本使用不同的特征权值得到预测标记，并通过某种策略将多个预测标记合并在一起得到最终所需要的预测结果。因此，一方面避免了单一特征组合对不同类型地物分类准确性的限制，而且在另一方面也降低了算法的计算复杂度和对特征数据的要求。本文算法有效地解决了上述特征处理困难和单一特征组合需要大量特征来实现多类图像分类的问题。另外，实测极化SAR图像数据的实验结果证明了本文算法与其他方法相比能够获得更好的分类结果。

2 所用到的极化特征及方法

因为雷达目标的电磁散射是一个线性过程，所以当散射空间坐标系以及相应的极化基被选定之后，就使得雷达照射波和目标散射波的各极化分量之间存在线性变换的关系，因此，一个复2维矩阵形式可以表示目标的变极化效应，称为极化散射矩阵[1]。极化SAR数据涵盖了地物类型的散射信息，是以矩阵形式作为表征，即每一个像素点均是一个矩阵，如式(1)所示：

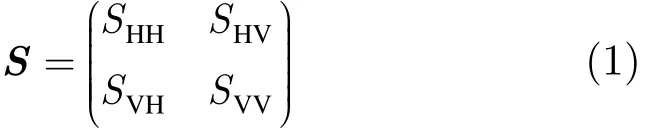
在分析极化数据过程中，通常将目标的极化散射矩阵矢量化。在后向散射情况下，因为互异性有SHV=SVH=Sx。由于极化相干矩阵更易于解释散射过程的物理意义[1,19]，所以在实际的极化研究中更多的是采用极化相干矩阵。在多视极化SAR图像中，每一个像素点都可以表示成一个3×3的正定Hermitite相干矩阵。

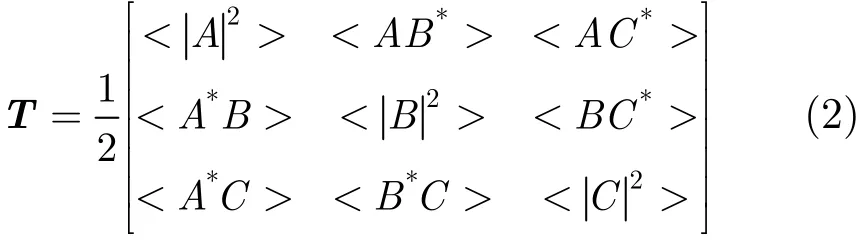
其中A=SHH+SVV, B=SHH−SVV, C=2Sx,＜·＞表示在假设随机散射机制各向同性下的空间统计平均。在假设随机介质的各向同性的情况下，T矩阵包含S矩阵中所有元素之间的偏差和相干信息。

基于目标散射理论，文献[3]将相干矩阵T表示为如式(3)形式，其中U3和λi(i=1,2,3)分别是矩阵T的特征矩阵和特征值，而上标H是共轭转置。

根据文献[3]，熵H定义为

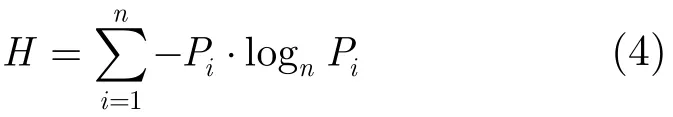
3 基于矩阵奇异值分解集成的监督极化SAR分类

3.1 基于0-1矩阵分解的加权集成

基于0-1矩阵分解的集成算法(SWENC)[18]是一种基于矩阵奇异值分解的加权集成算法。为了最小化集成误差，该方法通过对0-1矩阵进行奇异值分解所获得的系数将L个分类器合并在一起。根据文献[18]可以得到，在一个集成分类器系统中，集成的最终预测标记通常使用式(5)获得。

其中wi表示分类器Di的权值系数，pci表示分类器Di将样本x分到第c类的概率，c∈{1,2,…,C },L是个体分类器的数目。实际上，给分类器赋予权值的目的是为了能够降低集成误差。

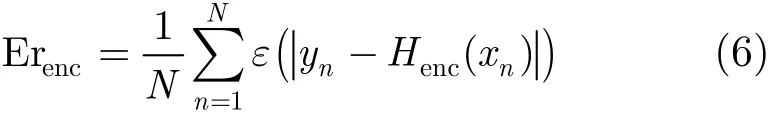
其中yn是样本xn的真实类别标记，N是样本数目，ε(·)表示当‘·’大于0，值为1，否则值为0。

在SWENC算法中，基于预测类别标记和真实类别标记来建立一个N×L维二进制矩阵A，并被用来表示集成中的个体分类器，其中元素用ani表示：

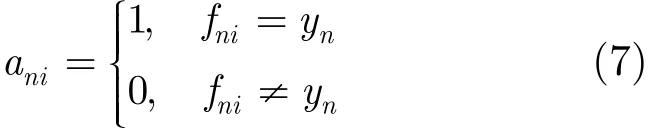
其中fni表示分类器Di(i=1,2,…,L)给予样本x的预测类别标记。因此，矩阵A的列向量表示分类器，而矩阵A列向量加和相当于分类器的分类性能。因此矩阵A奇异值分解后的右奇异值向量表明个体分类器在集成中的重要性。特别地，右奇异值矩阵中对应最大奇异值Σmax的右奇异向量vmax的平方就被用作个体分类器的线性组合系数权值。由理论分析可以得到：对于0-1矩阵来说，其奇异值越大，则基于该奇异值的奇异值向量所获得的集成分类误差就会越小。

3.2 基于矩阵分解集成算法的极化SAR图像分类

集成分类器作为集成学习在监督学习中的一个应用，它相当于结合多个分类器的预测标记从而提高单个分类器的分类性能的过程。根据文献[20]，差异性和个体分类器的误差是决定集成性能的两个非常关键的因素。然而，增加差异性是以提高了分类器的误差为代价的。这暗示了并不是所有的分类器都对提高集成性能有所帮助[20]。实际上，这与特征对于图像分类的影响是相似的，因为对于图像分类而言，并不是所有的特征都对某个图像处理取得好的效果。另外，不同的特征对于不同的数据、不同的图像，甚至同一个图像上的不同类别，其性能和贡献都是不一样的。那么，如果可以根据特征对于最终分类结果的贡献赋予其权值并进行调整，对于取得较好分类结果的特征给予较大的权值，而结果稍差一些的特征则分配较小的权值，那么就可以有效地提高图像分类的准确率。

因此，本文提出了一种新的基于分类器加权集成的极化SAR图像特征加权和监督分类方法。根据上面对极化SAR图像的介绍可知，极化SAR数据可以获得更多的关于散射的信息，但同时也给特征提取以及特征的应用带来更多的困难。目前极化SAR图像数据分类已经获得了广泛的关注，并且众多经典方法给出了除了相干矩阵之外的一些有用特征，但是这些特征如何使用和组合却还没有一个固定的结论。此外，因为地物散射信息存在随机性，雷达角度、地物自身倾角形状等因素的影响，导致属于不同类别的像素点可能存在相似的散射信息，而同一类别中的像素点却可能蕴含不同的散射信息[17]。这就意味着，对于不同的地物类型，甚至是对于同一地物类型的不同位置，每一个特征的有效性是不同的，那么对于所有像素采用单一的特征组合在有些情况下很难取得较好的分类结果。

而且，如果单纯靠增加特征维数，采用大量特征数据进行学习，其学习的复杂度也将相应提高。因此为了可以更有效地使用特征样本并降低学习复杂度，本文提出了一种基于0-1矩阵奇异值分解加权集成的极化SAR图像特征加权及监督分类的方法。该方法针对极化SAR图像数据，在极化SAR图像分类中，提取出多个特征作为原始特征集。再从中随机抽取若干特征组成不同的特征子集。然后对这些特征子集进行自学习，通过自学习结果和真实类标进行对比，得到0-1矩阵后进行奇异值分解，最后得到对应每一组个体的系数作为权值进行集成，用该加权集成之后的结果得到极化SAR图像的分类结果。下面将给出本文算法介绍和具体算法步骤。

特征处理是图像分类当中关键的步骤之一。在本文提出的方法当中，首先选取H/α方法[3]中的H/α/A，相干矩阵T中的对角线元素T11T22T33，上三角元素T12T13T23和相干矩阵的3个特征值作为初始的特征样本集。其中，相干矩阵T的对角线元素分别表示：目标的对称性因子，目标的非对称性因子和目标的非规则性因子；而上三角元素分别代表：构型因子和局部曲率差的度量，表面扭转和目标的螺旋性，对称与非对称部分间的耦合和目标的方向性[1]。因为相干矩阵T更容易解释关于散射过程的物理含义，从而其更多地被应用在实际的极化研究当中。因此相干矩阵T中的元素及相干矩阵分解的特征值通常作为极化SAR图像分类中特征。3个参数H,α,A分别代表着熵，alpha角和反熵，对应信息分别是[1,3]：角度α对应散射过程的物理机制，从α=0°到α=45°再到α=90°的变化依次对应表面散射、体散射和偶次散射变化；散射熵H表示散射媒质从H=0的各向同性散射到H=1完全随机散射的随机性；反熵A的大小反映了Cloude分解中优势散射机制以外的两个相对较弱的散射分量之间的大小关系，因此该3个元素可以很好地反映目标的物理机制及散射特性，也是极化SAR图像分类中的重要特征。

基于极化SAR原始图像选取一组像素点作为分类中已知标记的样本集，用表示，=，其中N表示已知其类别标记的样本数。因为机器学习算法被用在本文当中对极化SAR图像进行分类，所以这里将极化SAR图像中像素点对应于机器学习算法中的样本点，其中每一个像素点都具有多维特征。通过对原始特征集进行划分，获得m个不同的特征子集，其中每个子集都包含有d个特征。则对于类别标记已知的训练样本集而言，根据其中像素点所具有特征不同，可以写成m个不同的子集。然后，使用分类器算法对每个子集i(i=1,2,…,m)进行学习分类，获得对应每个子集的预测类别标记hi。根据对应每个子集i的预测标记hi，构造基于极化SAR图像的0-1矩阵。之后，对0-1矩阵A进行奇异值分解：A= UΣVT，再选取V中对应于最大特征值的向量vmax。该向量元素值的平方即为各个特征子集的对应系数权值。

基于0-1矩阵分解加权集成[18]原理，本文算法获得对应每个子集i的0-1矩阵(N×m)为

其中若预测标记与真实标记相同，则赋值1，若不相同，则赋值0。我们通过加权集成的方法得到了一个对应特征子集的权值向量。最终，每个基于特征子集得到的个体分类器的预测类别标记被赋予不同的权值从而合并在一起得到最终的分类结果。另外，本文中，0-1矩阵奇异值分解加权集成被用来对个体分类器进行加权，并且支撑向量机[21]被用作集成的基础分类器。下面将给出本文算法的详细步骤。

3.3 本文算法步骤

本文采用0-1矩阵分解加权集成框架对极化SAR图像进行分类的具体步骤如下：

步骤1 输入极化SAR图像，对其进行特征提取构成原始特征集X，另外，假设极化SAR图像有c类地物，Ω={ω1,ω2,…,ωC}；

步骤2 从原始特征集X中随机抽取m次，每次抽取d维特征构成m组特征子集{,,…,}；从极化SAR图像中选取出已知类标的样本集，其中每一个像素点ˆs均具有d维特征。则根据这m组特征子集，每一个像素点ˆs可以相应地得到m组不同个体，而样本集Sˆ可以写成子集{1,2,…,m}的组合。i(i=1,2,…,m)表示具有第i组特征的像素点集；

步骤5 将0-1矩阵A进行奇异值分解A= UΣVT，得到右侧矩阵V；

步骤6 选取其中对应最大特征值的特征向量vmax作为每一个子集的权值：2,…,m；

步骤7 根据权值系数将每个特征子集得到的预测标记集成在一起得到最终预测结果：H=

4 仿真实验及分析

本文选取3组实测极化SAR数据NASA/JPL AIRSAR L波段旧金山地区、CSA Radarsat-2 C波段旧金山地区和CSA Radarsat-2 C波段西安地区证明本文方法的有效性和稳定性。3个数据的原始图像见图1(a)，图2(a)和图3(a)。表1给出了3个实验数据的相关参数。

在本文实验当中，我们选取12个蕴含散射信息的特征作为原始特征集：分别是相干矩阵中的3个对角线元素，上三角3个元素，H,α,A和相干矩阵T的3个特征值。表2给出了实验中所用到的特征。

图2 原始图及分类结果

图3 原始图及分类结果

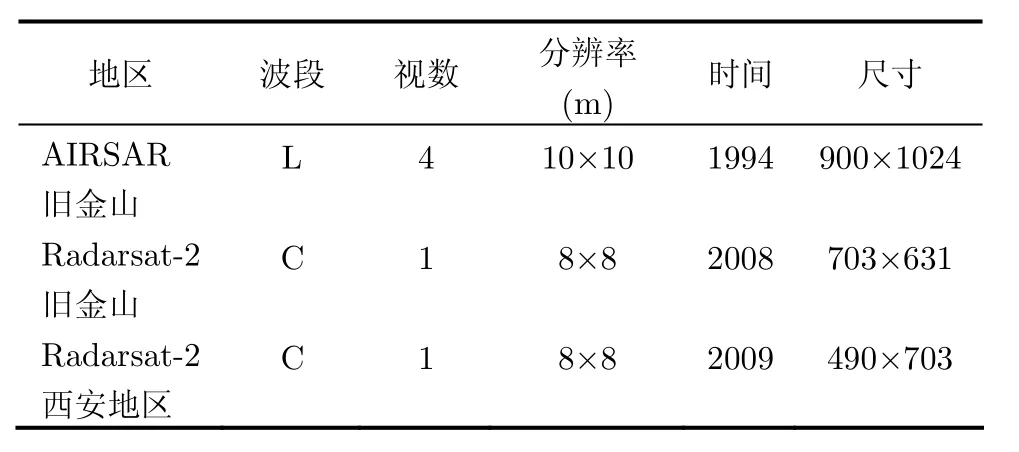
表1 分类中用到的特征

表2 分类中用到的特征

为了可以证明方法的有效性，我们将它与Wishart分类器和支撑向量机方法实验结果进行对比。在对比实验中，Wishart分类器用到特征是相干矩阵T中的9个元素；支撑向量机是直接使用表2中全部12维特征。而本文所提出的方法，选取表2中的12个特征作为初始特征集，然后从中随机选取15组，每组3个特征组成特征子集。

在实验当中，每一类选取1000个像素点作为极化SAR图像分类的初始训练样本，3类共选取3000个样本点。对于SVM分类器，我们使用的是RBF核，并且通过先验实验选取了合适的C和σ参数。表3给出了AIRSAR和Radarsat-2图像分类每一个实验所用的具体参数。另外，采用一对一的方法来处理多类问题。

4.1 AIRSAR L波段旧金山实验数据

NASA/JPL AIRSAR L波段旧金山数据是4视数据，尺寸是900×1024。本文中我们将该图像分为3类：植被、建筑物和水体。图1给出了原始图像和实验结果。

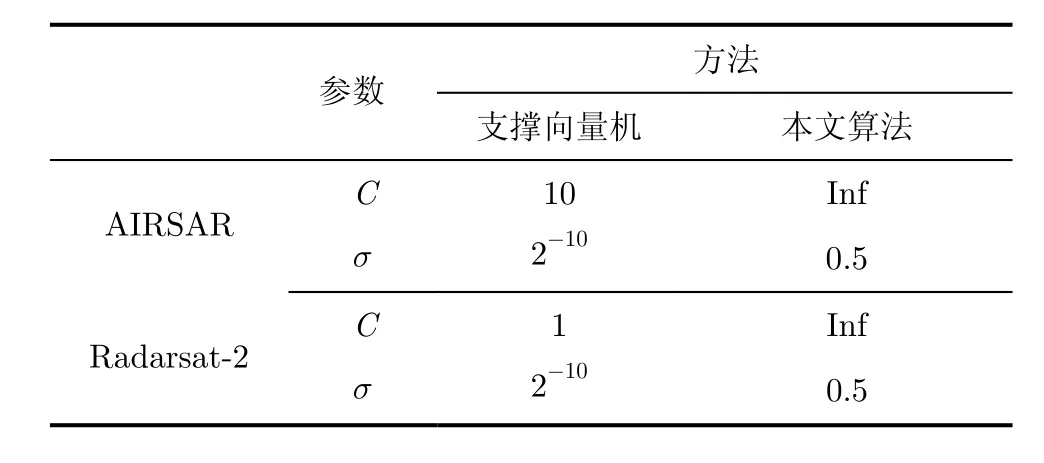
表3 分类中所采用的参数

从图1中的实验结果，可以清楚地看到，在建筑物和植被的分类上面，本文的算法明显优于Wishart分类器和支撑向量机的方法。在水体部分，Wishart算法在右上角海洋区域错分点较多，SVM算法在左侧海洋区域误分点较多，而本文算法得到了较好的结果。建筑物和植被的分类是极化SAR图像分类中的一个小难点，特别是建筑物和植被混杂的区域，通常会出现错分的现象。本文算法中，建筑物的轮廓更为清楚，区分更为明显。特别是对于左下角部分条状小路，本文算法的分类结果形状更为完整和准确。表4给出了实验的分类精度。分类精度是根据测试样本的真实类别标记和预测类别标记对比得出。已经在实验当中进行简短的补充。从分类精度我们可以看到，本文方法的分类精度均高于Wishart方法和支撑向量机方法，从而证明了本文方法的有效性。

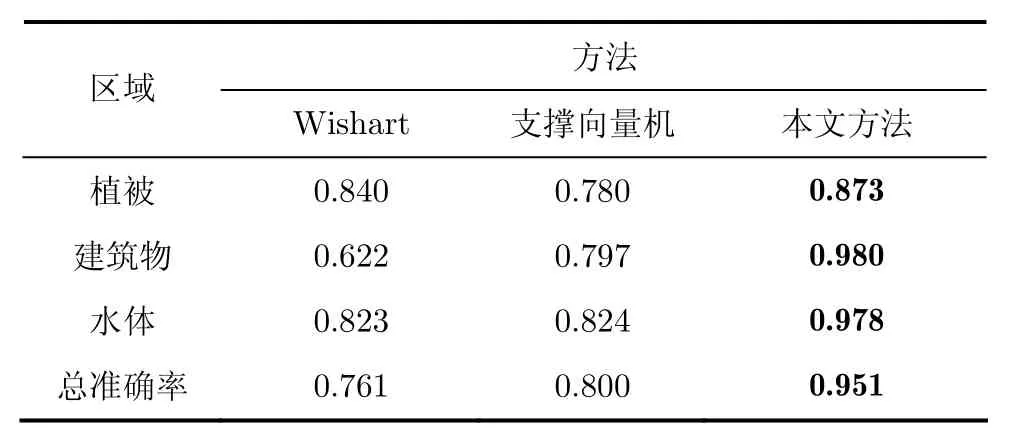
表4 AIRSAR旧金山分类精度

4.2 Radarsat-2 C波段旧金山实验数据

这里选取的实测极化数据是CSA Radarsat-2 C波段旧金山数据。这个数据依然是涵盖3种明显的地物类型：植被、建筑物和水体。该数据是单视图像，其尺寸是703×631。图2给出了原始图像和分类结果。

从实验结果中，可以明显看到，在水体区域，本文方法明显取得了更好的结果，分错的点最少。而且，在建筑物和植被两类地物的分类上，本文方法的结果两类区分更为明显，且轮廓和边界更加清晰。另外，表5中给出了Radarsat-2旧金山地区的分类精度。从表5中可以看到，本文方法取得了较高的准确率。

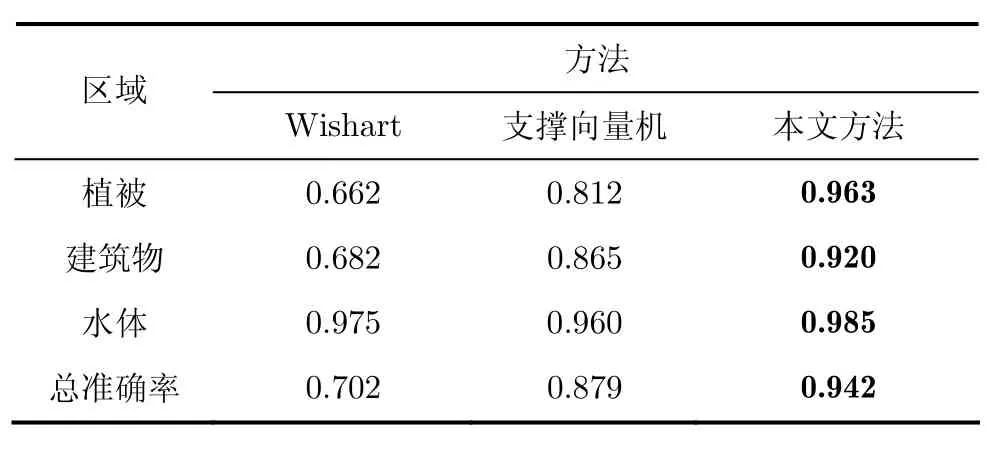
表5 Radarsat-2旧金山分类精度

4.3 Radarsat-2 C波段西安地区实验数据

这里用到的是Radarsat-2 C波段中国陕西西安市西部地区极化数据。该数据涵盖3种主要地物类型：植被，建筑物和水体。该数据截取尺寸是490×703。图3给出了原始图像和分类结果。从实验结果可以明显看到，本文方法将植被和建筑部分区分得更为明确，取得了较好的分类结果。从表6的分类精度中，也可以看到尽管本文方法在水体部分的分类准确率略低，但是在植被，建筑物和总的准确率上均有不同程度的提高。

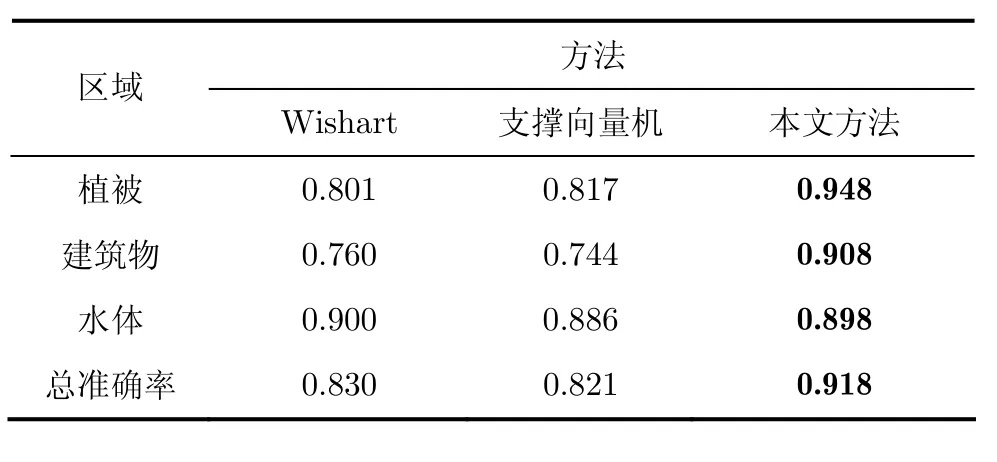
表6 Radarsat-2 西安地区分类精度

5 结束语

如何有效地应用特征并对特征进行加权是极化SAR图像分类非常重要的一个步骤。然而因为极化SAR数据的自身特性，单一的特征线性组合很难对多个类别同时产生很好的效果。本文方法将不同的特征组合所对应的结果通过集成策略合并在一起，取得了很好的结果。本文将原始特征组进行随机抽取得到多个特征子集，再根据这些特征子集训练得到多个分类器。最后用0-1矩阵奇异值分解加权集成策略给予多个分类器相应的权值系数来集成得到最后的极化SAR图像分类结果。多波段(C波段和L波段)多种类型(AIRSAR和Radarsat-2)的极化SAR实测数据也证明了本文方法的有效性和稳定性。本文算法目前针对的是监督极化SAR图像分类的特征加权，并且将集成方法应用在极化SAR图像处理当中。下一步研究方向将极化SAR经典分解算法与集成方法相结合，解决无监督和半监督极化SAR图像分类中的特征处理问题。

[1] Lee J S and Pottier E. Polarimetric Radar Imaging from Basic to Application[M]. New York: CRC Press, 2011: 1-51, 66-72, 229-247.

[2] Ding Tao, Anfinsen S N, and Brekke C. A comparative study of sea clutter covariance matrix estimators[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(5): 1010-1014.

[3] Cloude S R and Pottier E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518.

[4] Wang Chun-le, Yu Wei-dong, Wang Robert, et al.. Comparison of nonnegative eigenvalue decompositions with and without reflection symmetry assumptions[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(4): 2278-2286.

[5] Zhang Hong, Xie Lei, Wang Chao, et al.. Investigation of the capability of H-αdecomposition of compact Polarimetric SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(4): 868-872.

[6] Freeman A and Durden S L. A three-component scattering model for polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973.

[7] Jiao Zhi-hao, Yang Jian, Yeh Chun-mao, et al.. Modified three-component decomposition methord for polarimetric SAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 200-204.

[8] 刘高峰, 李明, 王亚军, 等. 一种改进的极化SAR自适应非负特征值分解[J]. 电子与信息学报, 2013, 35(6): 1449-1455.

Liu Gao-feng, Li Ming, Wang Ya-jun, et al.. An improved adaptive non-negative eigenvalue decomposition for polarimetric systhetic aperture radar[J]. Journal of Electronics & Information Technology, 2013, 35(6): 1449-1455.

[9] Yamaguchi Y, Moriyama T, Ishido M, et al.. Four-component scattering model for polarimetric SAR image decomposition [J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1699-1706.

[10] An W, Xie C, Yuan X, et al.. Four-component decomposition of polarimetric SAR image with deorientation[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1090-1094.

[11] 刘高峰, 李明, 王亚军, 等. 基于层次非负特征值约束的Yamaguchi分解[J]. 电子与信息学报, 2013, 35(11): 2678-2685.

Liu Gao-feng, Li Ming, Wang Ya-jun, et al.. Yamaguchi decomposition based on hierarchical nonnegative eigenvalue restriction[J]. Journal of Electronics & Information Technology, 2013, 35(11): 2678-2685.

[12] Liu Gao-feng, Li Ming, Wang Ya-jun, et al.. Four-component scattering power decomposition of remainder coherency matrices constrained for nonnegative eigenvalues[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 494-498.

[13] Lee J S, Grunes M R, and Kwok T. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution[J]. International Journal of Remote Sensing, 1994, 15(11): 2299-2311.

[14] Fukuda S and Hirosawa H. Support vector machine classification of land cover: application to polarimetric SAR data[C]. IEEE International Geoscience And Remote Sensing Symposium (IGARSS'01), Sydney, Australia, 2001: 187-189.

[15] Fukuda S, Katagiri R, and Hirsosawa H. Unsupervised approach for polarimetric SAR image classification using support vector machines[C]. IEEE International Geoscience And Remote Sensing Symposium (IGARSS'02), Toronto, Canada, 2002, 5: 2599-2601.

[16] Kumar S, Ghosh J, and Crawford M. Best-bases feature extraction algorithm for classification of hyperspectral data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(7): 1368-1379.

[17] 徐丰, 金亚秋. 目标散射的去取向理论和应用(一)去取向理论[J]. 电波科学学报, 2006, 21(1): 6-15.

Xu Feng and Jin Ya-qiu. Theory and application of deorientation for target scattering Part I: deorientation theory[J]. Chinese Journal of Radio Science, 2006, 21(1): 6-15.

[18] Mao Sha-sha, Xiong Lin, Jiao Li-cheng, et al.. Weighted ensemble based on 0-1 matrix decomposition[J]. Electronics Letters, 2013, 49(2): 116-118.

[19] Henri Maitre. 孙洪, 等译. 合成孔径雷达图像处理[M]. 北京:电子工业出版社, 2005: 第4章.

[20] Kuncheva L I. Combining Pattern Classifiers: Methods and Algorithms[M]. Hoboken, New Jersey, John Wiley & Sons, 2004: Chapter 1.

[21] Christopher J C B. A tutorial on support vector machine for pattern recognition[J]. Data Mining and Knowledge Discovery, 1998, 2(2): 121-167.

陈 博： 女，1985年生，博士生，研究方向为极化SAR图像处理.

王 爽： 女，1978年生，教授，主要研究领域为多尺度几何分析、图像处理.

焦李成： 男，1959年生，教授，博士生导师，主要研究领域为自然计算、智能信息处理等.

刘 芳： 女，1963年生，教授，博士生导师，主要研究领域为智能信息处理、图像的感知与识别、数据挖掘等.

毛莎莎： 女，1985年生，博士生，研究方向为集成算法与图像处理.

张 爽： 女，1983年生，博士生，研究方向为极化SAR图像处理.

Polarimetric SAR Image Classification via Weighted Ensemble Based on 0-1 Matrix Decomposition

Chen Bo①Wang Shuang①Jiao Li-cheng①Liu Fang②Mao Sha-sha①Zhang Shuang①

①(Key Laboratory of Intelligent Perception and Image Understanding of Ministry of Education, Xidian University, Xi'an 710071, China)

②(School of Electronic Engineering, Xidian University, Xi'an 710071, China)

For Polarimetric SAR (PolSAR), because it contains more scattering information, thus it can provide more available features. How to use the features is crucial for the PolSAR image classification, however, there are no existing specific rules. To solve the above problem, a supervised Polarimetric SAR image classification method via weighted ensemble based on 0-1 matrix decomposition is proposed. The proposed method adopts matrix decomposition ensemble to learn on different feature subsets to get coefficients, and weighting ensemble algorithm is employed via the predictive results to improve the final classification results. Firstly, some features are extracted from PolSAR data as initial feature group and are divided randomly into several feature subsets. Then, according to the ensemble algorithm to get the different weights based on the feature subsets, small coefficients are assigned to bad classification results to decrease the harmful impact of some features. The final classification result is achieved by combining the results together. The experimental results of L-band and C-band PolSAR data demonstrate that the proposed method can effectively improve the classification results.

Polarimetric SAR (PolSAR); Supervised image classification; Ensemble learning; Classifier ensemble

TP751

： A

：1009-5896(2015)06-1495-07

10.11999/JEIT141059

2014-08-11收到，2014-10-22改回

国家973计划项目(2013CB329402)，国家自然科学基金(61271302, 61272282, 61202176, 61271298)和国家教育部博士点基金(20100203120005)资助课题

*通信作者：陈博 chenbo8505@163.com