基于L1-范数的二维线性判别分析
2015-07-12陈思宝陈道然
陈思宝陈道然 罗 斌
(安徽大学计算机科学与技术学院 合肥 230601)
(安徽省工业图像处理与分析重点实验室 合肥 230039)
基于L1-范数的二维线性判别分析
陈思宝*陈道然 罗 斌
(安徽大学计算机科学与技术学院 合肥 230601)
(安徽省工业图像处理与分析重点实验室 合肥 230039)
为了避免图像数据向量化后的维数灾难问题,以及增强对野值(outliers)及噪声的鲁棒性,该文提出一种基于L1-范数的2维线性判别分析(L1-norm-based Two-Dimensional Linear Discriminant Analysis, 2DLDA-L1)降维方法。它充分利用L1-范数对野值及噪声的强鲁棒性,并且直接在图像矩阵上进行投影降维。该文还提出一种快速迭代优化算法,并给出了其单调收敛到局部最优的证明。在多个图像数据库上的实验验证了该方法的鲁棒性与高效性。
图像处理;L1-范数;2维线性判别分析;线性投影;降维
1 引言
在模式识别和图像处理领域,由于所处理的图像维数特别高,而训练样本数量又非常有限,经常导致“维数灾难”问题[1]。此外,在高维空间中存在着测度的“集中现象”,为了克服这些问题并且使得后续的数据表示或分类更加稳健,对高维数据进行降维就成了一个非常重要的步骤。
众所周知,最为经典的线性投影降维方法通常将高维训练数据用向量形式进行表示,再进行线性投影降维和特征提取,其中基于向量的1维线性投影降维方法主要有主成分分析(Principal Component Analysis, PCA)[2,3],线性判别分析(Fisher Linear Discriminant Analysis, FisherLDA)[1,2], PCA+LDA[4]等。然而,1维方法通常将图像数据拉直成向量形式,其维数通常非常高,但训练数据又非常有限,这通常导致矩阵计算的不稳定,出现矩阵奇异问题。针对1维方法所遇到的问题,许多学者又提出了直接基于图像矩阵的线性投影降维方法,即2维线性投影降维方法。经典的2维方法有2维主成分分析(Two-Dimensional PCA, 2DPCA)[5,6]和2维线性判别分析(Two-Dimensional LDA, 2DLDA)[7−9]。然而,这些1维的和2维的线性投影降维方法都基于L2-范数来计算相应的目标函数。当训练数据中存在野值或噪声时,计算所得到的投影方向会严重受到这些野值或噪声的影响。
最近,一些文献中出现了基于L1-范数[10−16]的线性投影降维方法,诸如:基于L1-范数的PCA (L1-norm based PCA, PCA-L1)[12]、基于旋转不变L1-范数的LDA(Rotational invariant L1-norm based LDA, LDA-R1)[13]、基于L1-范数的LDA(L1-norm based LDA, LDA-L1)[14,15]及基于L1-范数的2DPCA(L1-norm based 2DPCA, 2DPCAL1)[16]。这些基于L1-范数的线性投影降维方法均对野值及噪声表现出了很强的鲁棒性。但是,PCA-L1, LDA-R1和LDA-L1都把图像数据进行了向量化预处理,并没有充分利用图像数据固有的矩阵形式,破坏了图像数据原有的空间结构关系。2DPCA-L1着重利用图像数据矩阵来提取低维特征,但它没有充分利用训练数据中的类别信息以提高投影方向的判别性能。
本文提出的2DLDA-L1线性投影降维方法不仅充分利用L1-范数对野值及噪声的强鲁棒性,而且直接对图像数据矩阵进行线性投影,减少了图像数据空间的信息丢失,并且避免了图像向量化后的高维矩阵的庞杂计算及解的不稳定性。相比于以前的方法对野值及噪声具有更强的鲁棒性,并且在分类识别的性能上取得了显著提升。
本文其余部分的结构安排如下:第2节先提出2DLDA-L1最优投影方向的目标优化函数,然后给出一种优化迭代方法,最后给出多重投影方向的完整2DLDA-L1算法并分析算法的复杂度;第3节在多个图像数据库上实验验证所提出的2DLDA-L1算法的判别性能及鲁棒性能,并给出相应的实验结果及分析;第4节为结束语。
2 基于L1-范数的2维线性判别分析(2DLDA-L1)
2.1 2DLDA-L1最优投影方向


采用w(t+1)=w(t)+γg(w(t ))来更新2DLDAL1最优投影向量w(t),其中

γ>0为学习步长,g(w(t))的获得见文献[14]。循环交替计算式(2)的符号函数及式(3)的梯度公式来求解2DLDA-L1最优投影向量w。在迭代过程中,若目标函数J(w(t+1))停止增长,则终止循环。否则,更新式(2)并继续循环,直到找到满足条件的投影向量w。
可以证明:在每次循环计算式(2)与式(3)后,式(1)中的目标函数J(w(t+1))都保持非降。另外,J函数存在上界(当目标函数J 在分母约束恒为 1 时,根据文献[17,18]中的定理,可知其上界为图像类间离散度矩阵的最大特征值),因此,循环计算式(2)与式(3)的迭代过程逐渐收敛。然而,通过迭代算法所求的投影向量w可使目标函数J达到局部最优,但并不能保证J达到全局最优。由于篇幅有限,此处略去详细证明,具体证明方法可以参考文献[14]。
2.2 2DLDA-L1多个投影方向扩展
前面所述的迭代优化求解方法仅计算2DLDAL1的一个最优投影方向,这不利于实际应用,故需要扩展到求取多个投影方向。设已得到第1个最优投影轴为w1,我们在w1的正交补空间中寻求第2个最优投影轴w2,即在w1的正交补空间中最大化式(1)。w1的正交补空间为Is−w1,其中Is表示一个s维的单位矩阵。故存在一个向量b1∈Rs,使w2=(Is−w1)b1。代入w2到式(1)中,得
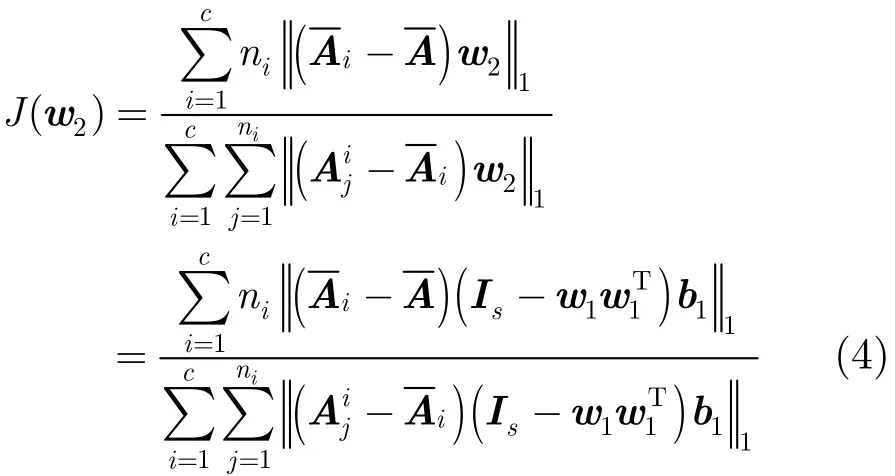

同样,由2.1节的迭代算法可解出b1。再根据公式w2=(Is−w1)b1,便可得到第2个投影轴w2,并归一化
设已获得l个最优投影轴w1w2…wl,则第l+1个最优投影轴wl+1可在正交向量w1w2…wl的正交补空间中寻求,其中w1w2…wl的正交补空间为
Is−Wl,投影矩阵Wl=[w1w2…wl]。同样存在一个向量bl∈Rs,使wl+1=(Is−Wl)bl,则bl可迭代优化由新数据矩阵A=(Is−Wl)计算的式(1)来求出。注意到
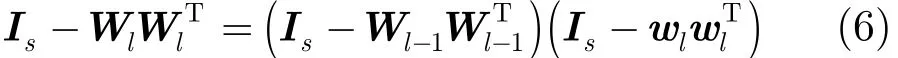
2.3 2DLDA-L1计算复杂度分析
对于含有c个类别共n个(m×s)大小的图片训练数据集,所提出的2DLDA-L1最耗时的是两重循环内部的步骤2(3)计算符号函数与(4)计算梯度方向,它们的计算复杂度分别为O((cm+nm)s)和O(2(cm+nm)s)。因此,若欲每次内循环迭代t次,共提取q个投影方向轴,则整个2DLDA-L1的计算复杂度为O((cm+nm)stq)。在相同的数据集上,与之相对应的2DLDA的计算复杂度为O((n+c)ms2+s3)。LDA-L1的计算复杂度为O((c+n)mstq),最耗时的是两重循环内部的计算符号函数与计算梯度方向。LDA-R1的计算复杂度为O((n+c)m2s2tq2),最耗时的是其中的特征值分解。LDA的计算复杂度为O((n+c)m2s2+m3s3),最耗时的是求解广义特征向量。

表1 基于L1-范数的2维线性判别分析(2DLDA-L1)
3 实验结果及分析
为了验证本文所提出的2DLDA-L1方法的鲁棒性及最终识别性能,本文选择在3个常用的人脸图像数据库(PIE[19], AR[20]及ORL[21])上进行先降维后分类识别的对比实验。在实验中,我们选择4种对比方法,分别是LDA, LDA-R1, LDA-L1和2DLDA。为了保证实验结果的公平与合理性,同类实验中的参数设置均一致。为简化实验,我们仅采用最近邻分类器进行分类识别。
3.1 PIE人脸数据库

图1 J(w(t))随着迭代次数t的变化趋势
PIE人脸数据库提供了不同姿态、光照、表情条件下68位志愿者的40000多幅不同的图像,每一幅图像都是在严格控制的条件下采集的。本文在其中一个子集共17000幅图像上进行测试,即随机提取出68人每人24幅图像作为PIE子库。所有的人脸图像都被缩放到32×32大小,量化到256级灰度。
3.1.1 目标函数的迭代收敛性 2.1节中提到了目标函数J(w(t))是非降的并逐渐收敛到局部最优。在这一部分,我们验证2DLDA-L1的目标函数J(w(t))的局部最优化,并与迭代次数t之间的关系。实验结果如图1所示。
图1表明,在提取投影向量的过程中,随着迭代次数的逐渐增加,目标函数J(w(t))逐渐递增并达到局部最大。
3.1.2 步长参数γ的影响
为了验证梯度法w(t+1)=w(t)+γg(w(t ))中更新步长参数γ的影响,我们从集合{0.01,0.05,0.1,0.5, 1,5,10,50,100,500,1000}中选择不同的γ值测试其对收敛性及识别率的影响。实验结果如图2所示。
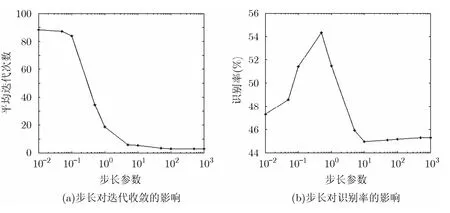
图2 步长参数γ的影响
图2(a)和2(b)充分说明γ不仅影响算法的收敛速度而且还影响算法的识别性能。由于2DLDA-L1中的目标函数并不是全局严格凸的,一个固定的γ值易使迭代算法中的目标函数局部最优化,因此在运行实验时,我们随机选择不同的γ值来优化目标函数,并选取使得目标函数达到最大的参数。
3.2 AR人脸数据库
AR人脸数据库由西班牙巴塞罗那计算机视觉中心建立,包括3120幅图像,共120个人,每人26幅图像,采集环境中的摄像机参数、光照环境、摄像机距离等都受到严格控制。所有人脸图像都被缩放到32×32大小,量化到256级灰度。
3.2.1 投影轴数q对识别率的影响 线性投影降维是处理高维数据的一个重要步骤。为了验证不同的投影轴数对识别率的影响,本节依次选择1,2,…,20个投影轴数进行测试。实验结果如图3所示。
图3表明,随着投影轴数的逐渐增加,各种方法的识别率都会达到一个饱和值。但是,当投影轴数相同时,2DLDA-L1方法的识别率比其它方法的识别率高。
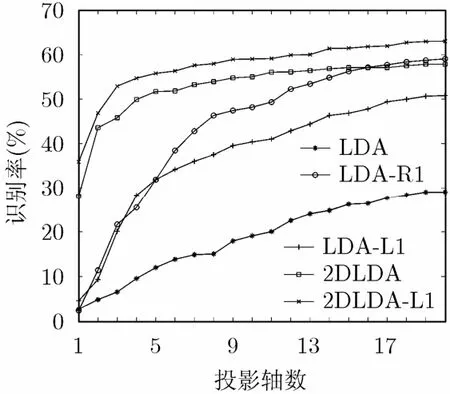
图3 识别率随着不同投影轴数q的变化趋势
3.2.2 噪声的影响 为了验证2DLDA-L1对噪声的鲁棒性,本节在加有高斯噪声或椒盐噪声的人脸图像上进行对比分类识别实验。图4(a)和图4(b)分别为加入高斯噪声和椒盐噪声后的图像示例,图像加入高斯噪声的方差或椒盐噪声的密度从小到大依次为0.0001, 0.0005, 0.001,0.005, 0.01, 0.05, 0.1。实验结果如图5所示。

图4 加入噪声示例
图5表明,随着噪声方差或密度的逐渐增加,各种方法的识别率逐渐降低。但是2DLDA-L1的识别率一直最高,这说明2DLDA-L1具有更好的鲁棒性。
3.3 ORL人脸数据库
ORL数据库是一个最为常用的人脸数据库,它由40个人,每个人10幅92×112的灰度人脸正面图像组成,每张人脸图像都有姿态、表情和面部饰物的变化。所有的人脸图像都被缩放到32×32大小,量化到256级灰度。
3.3.1 不同训练集大小对识别率的影响 为了验证不同的训练集大小对识别率的影响,每类中前k(k=2, 3,…,7)幅图像作为训练集,余下的作为测试集。实验效果如图6所示。
图6表明,同等条件下,随着训练样本数目的增多,各种方法的识别率逐渐增高,而2DLDA-L1的识别率一直最高,这充分说明2DLDA-L1方法的高效性。
3.3.2 部分缺失遮挡的影响 本节对人脸图像设置不同比例的缺失或遮挡,以验证所提出的2DLDA-L1的鲁棒性。设置图像缺失或遮挡的百分比分别为5%, 10%,15%,20%,25%,30%,35%,40%,45%,50%。图7(a)为不同比例块随机缺失示例,图7(b)为不同比例块随机遮挡示例。实验结果如图8所示。
图8表明,随着图像随机缺失或遮挡的百分比逐渐增加,2DLDA算法的识别率有很大的波动而其它算法的识别率整体趋势都在逐渐下降。然而,当有相同比例的缺失或遮挡时,2DLDA-L1方法的识别率比其它算法的识别率高,这说明2DLDA-L1具有更强的鲁棒性。
4 结束语
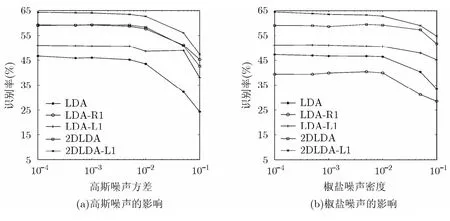
图5 噪声对识别率的影响
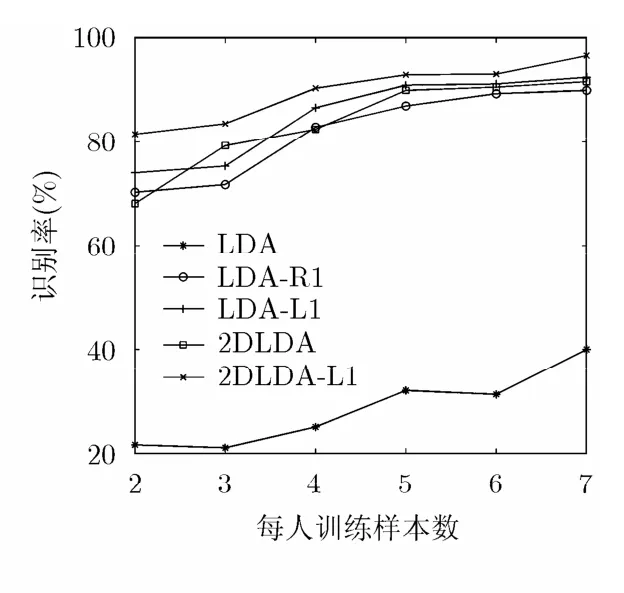
图6 识别率随着不同训练集大小的变化趋势
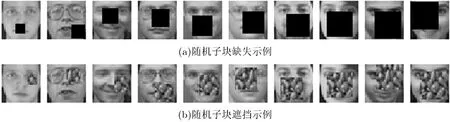
图7 图像随机子块缺失遮挡示例

图8 不同比例缺失遮挡对识别率的影响
本文在LDA, LDA-L1和2DLDA方法的基础上,提出基于L1-范数的2维线性判别分析(2DLDAL1)。该方法充分利用L1-范数对野值及噪声的强鲁棒性,并且直接在图像数据矩阵上进行线性投影降维,减少了图像数据空间的信息丢失以及避免了向量化图像数据出现的维数灾难。提出了一个单调优化迭代算法来求解其最优投影矩阵,并给出了其单调收敛到局部最优的证明。在多个图像数据库上的实验结果表明,本文提出的2DLDA-L1对野值及噪声具有强鲁棒性,并且比其它方法具有更好的判别性能。注意到,本文方法仅仅是收敛到局部最优。在后续的工作中,我们将继续深入研究如何找到全局最优。
[1] Duda R, Hart P, and Stork D. Pattern Classification[M]. Second edition, New York: John Wiley & Sons, 2001: 2-5.
[2] Chan L, Salleh S, Ting C, et al.. Face identification and verification using PCA and LDA[C]. International Malaysia, 2008: 1-6.
[3] Rujirakul K, So-In C, Arnonkijpanich B, et al.. PFP-PCA: parallel fixed point PCA face recognition[C]. 2013 4th International Conference on Intelligent Systems, Modelling Symposium on Information Technology, Kuala Lumpur, and Simulation, Bangkok, 2013: 29-31.
[4] Belhumeur P, Hespanha J, and Kriegman D. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(7): 711-720.
[5] Yang Jian, Zhang D, Frangi A, et al.. Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(1): 131-137.
[6] Wang Shi-min, Ye Ji-hua, and Ying De-quan. Research of 2DPCA principal component uncertainty in face recognition[C]. 2013 8th International Conference on Computer Science & Education, Colombo, Sri Lanka, 2013: 159-162.
[7] Li Ming and Yuan Bao-zong. A novel statistical linear discriminant analysis for image matrix: two-dimensional 527-532.
[8] Mahanta M and Plataniotis K. Ranking 2DLDA features based on fisher discriminance[C]. IEEE International Conference on Acoustic, Speech and Signal Processing, Fisherfaces[J]. Pattern Recognition Letters, 2005, 26(5): Florence, Italy, 2014: 4-9.
[9] Wang Bin-bin, Hao Xin-jie, Chen Li-sheng, et al.. Face recognition based on the feature fusion of 2DLDA and LBP[C]. 2013 Fourth International Conference on Information, Intelligence, Systems and Applications, Piraeus, Greece, 2013: 10-12.
[10] Pang Yan-wei, Li Xue-long, and Yuan Yuan. Robust tensor analysis with L1-norm[J]. IEEE Transactions on Circuits Syst ems for Video Techology, 2010, 20(2): 172-178.
[11] Zheng Wen-ming, Lin Zhou-chen, and Wang Hai-xian. L1-norm kernel discriminant analysis via Bayes error bound optimization for robust feature extraction[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 793-805.
[12] Kwak N. Principal component analysis based on L1-norm maximization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(9): 1672-1680.
[13] Li Xi, Hu Wei-ming, Wang Han-zi, et al.. Linear discriminant analysis using rotational invariant L1 norm[J]. Neurocomputing, 2010, 73(13): 2571-2579.
[14] Wang Hai-xian, Lu Xue-song, Hu Zi-lan, et al.. Fisher discriminant analysis with L1-norm[J]. IEEE Transactions on Cybernetics, 2013, 44(6): 828-842.
[15] Zhong Fu-jin and Zhang Jia-shu. Linear discriminant analysis based on L1-norm maximization[J]. IEEE Transactions on Image Processing, 2013, 22(8): 3018-3027.
[16] Li Xue-long, Pang Yan-wei, and Yuan Yuan. L1-norm-based 2DPCA[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2010, 40(4): 1170-1175.
[17] Wang Hai-xian, Tang Qin, and Zheng Wen-ming. L1-normbased common spatial patterns[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(3): 653-662.
[18] Jenatton R, Obozinski G, and Bach F. Structured sparse principal component analysis[C]. International Conference on Artificial Intelligence and Statistics, Paris, France, 2009: 1-8.
[19] Gross R, Matthews I, Cohn J, et al.. Multi-PIE[C]. 8th IEEE International Conference on Automatic Face & Gesture Recognition, Amsterdam, The Netherland, 2008: 1-8.
[20] Martinez A and Benavente R. The AR face database[R]. CVC Technical Report 24, Barcelona, Spain, 1998.
[21] Samaria F and Harter A. Parameterisation of a stochastic model for human face identification[C]. Proceedings of the Second IEEE Workshop on Applications of Computer Vision, Sarasota, USA, 1994, 138-142.
陈思宝: 男,1979年生,副教授,硕士生导师,研究方向为图像处理与模式识别.
陈道然: 女,1989年生,硕士生,研究方向为图像处理与模式识别.
罗 斌: 男,1963年生,教授,博士生导师,研究方向为计算机视觉与模式识别.
L1-norm Based Two-dimensional Linear Discriminant Analysis
Chen Si-bao Chen Dao-ran Luo Bin
(School of Computer Science and Technology, Anhui University, Hefei 230601, China)
(Key Laboratory for Industrial Image Processing and Analysis of Anhui Province, Hefei 230039, China)
To overcome the curse of dimensionality caused by vectorization of image matrices, and to increase robustness to outliers, L1-norm based Two-Dimensional Linear Discriminant Analysis (2DLDA-L1) is proposed for dimensionality reduction. It makes full use of strong robustness of L1-norm to outliers and noises. Furthermore, it performs dimensionality reduction directly on image matrices. A rapid iterative optimization algorithm, with its proof of monotonic convergence to local optimum, is given. Experiments on several public image databases verify the robustness and the effectiveness of the proposed method.
Image processing; L1-norm; Two-Dimensional Linear Discriminant Analysis (2DLDA); Linear projection; Dimensionality reduction
TP391.4
: A
:1009-5896(2015)06-1372-06
10.11999/JEIT141093
2014-08-18收到,2015-02-04改回
国家自然科学基金(61202228)和安徽省高校自然科学研究重点项目(KJ2012A004)资助课题
*通信作者:陈思宝 sbchen@ahu.edu.cn
