基于功率中值和归一化采样协方差矩阵的自适应匹配滤波检测器

刘 明水鹏朗

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

基于功率中值和归一化采样协方差矩阵的自适应匹配滤波检测器

刘 明*水鹏朗

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

在非均匀海杂波环境中，参考单元中的异常单元限制了采样协方差矩阵(SCM)的估计性能，从而影响了传统自适应匹配滤波(AMF)检测器的检测性能。而考虑删除异常单元的方法在参考单元数目有限时可能导致矩阵的奇异性。鉴于此，在保持参考单元数目不变条件下，该文设计一种基于功率中值与归一化采样协方差矩阵(MNSCM)的估计方法，并将其与匹配滤波器(MF)相结合，构造一种新型的自适应匹配滤波检测器。与传统的自适应匹配滤波相比，该文设计的检测器在实测和仿真海杂波数据条件下均具有明显的性能优势。

目标检测；海杂波；自适应匹配滤波器；采样协方差矩阵；功率中值和归一化采样协方差矩阵

1 引言

海杂波背景下的动目标检测问题因其具有重要的战略意义和民用价值，一直以来备受国内外学者关注[1−4]。由于海杂波具有平均功率大，时空相关性强和统计特性复杂等特点，使其成为目标检测问题中的一个研究难点。虽然海杂波在短时间内可认为是平稳的，但从长时间来看，海杂波具有明显的空时非平稳性[5,6]。因此，对于海杂波背景下的动目标检测问题，通常会选用自适应检测算法处理此类检测问题。

自适应匹配滤波[7]作为一种常见自适应检测算法。它使用了各个距离单元的多脉冲匹配结果作为检测统计量，从而实现目标检测。但使用该方法之前首先要对待测单元的杂波协方差矩阵进行估计。在杂波均匀假设下，即在待测单元与其邻近的距离单元(参考单元)共用同一个协方差矩阵条件下，可以使用由参考单元构成的采样协方差矩阵(Sample Covariance Matrix, SCM)估计待测单元的杂波协方差矩阵。然而，均匀杂波环境假设在实际检测下往往并不满足。

在雷达高分辨条件下或低擦地角观测下，杂波数据的呈现出很强的非高斯特性，杂波中含有大量类似目标的尖峰信号[8,9]，这种尖峰信号的存在会影响SCM的估计性能[10]。关于高分辨率条件下杂波的统计特性，国内外诸多学者对其进行了详细地研究。其中，文献[5]分析了X波段不同分辨率条件下杂波的统计特性；文献[11]分别采用几种经典统计模型给出了L波段杂波在不同环境参数条件下的幅度最优分布模型。虽然不同条件下获得的杂波幅度分布模型有所不同，但这些分布几乎都可以归类为同一个分布，即复合高斯分布(在常见的杂波模型中，Lognormal分布不属于此类)。然而，实际工作环境中的复合高斯分布的统计特性是事先未知的，尤其是杂波的协方差矩阵，这就需要我们从数据中进行估计。由于高分辨条件下的杂波不满足均匀性假设，并且实际检测中并不清楚哪个距离单元中含有目标信号。因此，选取的参考单元中可能含有目标或者杂波特性明显不同于待测单元的单元，本文称这样的单元为异常单元。当使用含有异常单元的参考单元估计协方差矩阵时，势必使SCM的出现性能损失。

为了避免异常单元对SCM估计性能的影响，文献[12]使用一种数据自适应筛选(Data-Adaptive Selection, DAS)方法获取均匀杂波数据。文献[13]采用两步自动删除平均水平的方法获得均匀杂波数据。上述方法的共同点是对参考单元作预处理，剔除其中含有的异常单元，以获取相对均匀杂波数据。然而，当参考单元数目较少时，删除其中一些异常单元也会使SCM的估计性能下降甚至出现协方差矩阵的奇异性。在不改变参考单元数目条件下，本文设计一种基于功率中值和归一化采样协方差矩阵(Median Normalized Sample Covariance Matrix, MNSCM)的协方差矩阵估计方法。它能够有效抑制非均匀杂波环境下由于不同距离单元间功率起伏对协方差矩阵估计性能带来的影响，与此同时，它保留杂波的功率信息，使其能够适用于匹配滤波(Matched Filter, MF)检测器。

实验部分分别采用实测和仿真的杂波数据对基于中值和归一化采样协方差矩阵的自适应匹配滤波(Median Normalized Sample Covariance Matrix-Adaptive Matched Filter, MNSCM-AMF)检测器的有效性作了验证。对于实测数据，选取参考单元时人为将一些功率大的异常单元考虑在内；对于仿真数据，通过调高参考单元中的某些距离单元的功率，以便获得一种含有异常单元的杂波数据。对于这两种数据，MNSCM-AMF检测器均获得了比基于采样协方差矩阵的自适应匹配滤波(SCM-AMF)检测器更好的检测结果。同时，通过调整仿真的杂波环境的非均匀程度，即异常单元的功率大小和所占的比例，定量地分析MNSCM-AMF检测器在不同程度的非均匀杂波环境相比SCM-AMF检测器具有更优检测结果的原因。

文章其余部分安排如下，第2节对检测问题进行简要描述；第3节首先引入传统的自适应匹配滤波检测器，随后介绍基于中值和归一化采样协方差矩阵的自适应匹配滤波检测器；第4节通过实验方式验证MNSCM-ANMF检测器相比SCM-ANMF检测器的检测性能优势，并在仿真数据条件下，定量分析了两种检测器性能差异产生的原因；第5节总结全文。

2 检测问题描述

如果复信号z(t)表示待测单元在观测时间内的接收到的海杂波的基带形式，对这一基带信号进行采样得到接收向量z=zI+jzQ，其中，zI和zQ分别代表接收向量z的同相部分和正交部分。要判断采样所得的向量z中是否含有目标信号相当于式(1)所示的二元假设检验：

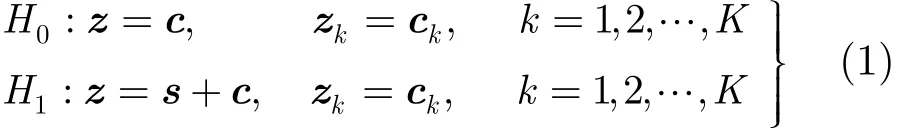
其中，z, s和c分别代表待测单元中的N维接收向量，感兴趣的目标信号和待测单元中的杂波向量；zk或者ck,k=1,2,…,K ，是来自参考单元中不含目标信号的一组接收向量，并假定在H0假设下zk与z具有相同的协方差矩阵。在此假定下，当待测单元接收向量z中的杂波协方差矩阵未知时，可以使用参考单元数据zk估计待测单元中的杂波协方差矩阵。这里假定K＞2N以满足输出的信杂比的损失小于3 dB。

在相干处理中，目标信号s可以看作一个相干脉冲序列，即s=αp，其中，α是与传输信道和雷达横截面积有关的常量，p是多普勒导向矢量，p=[1 exp(j2πfdTr) … exp(j2π(N−1)fdTr)]T，其中，fd是目标的多普勒频率，Tr是雷达脉冲重复间隔。对于杂波向量c，采用复合高斯模型进行建模，即杂波可以看作是复高斯分布的散斑分量u(n)和非负的纹理分量τ(n)的乘积，其中，相比散斑分量，纹理分量具有更长的去相关时间[9,14]。因此，当观测时间在几个相干处理时间内时，复合高斯分布的纹理分量τ(n)可以近似为某一常数，此时的复合高斯模型退化为球不变随机向量(Spherically Invariant Random Vector SIRV)模型，即c=u。

3 两种自适应匹配滤波检测器

针对式(1)中的检测问题，自适应匹配滤波(AMF)检测器给出如下检测方案。当杂波协方差矩阵已知时，由似然比不难得到AMF检测器的检测统计量为

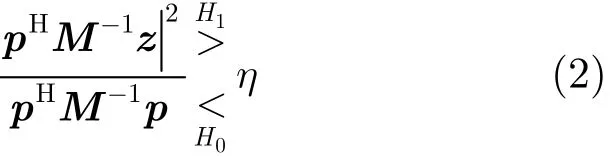
其中，M是真实的杂波协方差矩阵, η是满足指定虚警概率条件下的判决门限。然而，在实际工作环

将式(2)中的M替换为式(3)，从而得到均匀杂波环境中传统的AMF检测器。境中，杂波的协方差矩阵往往是未知的，需要从参考单元数据中估计得到。在杂波均匀假设前提下，可以使用SCM得到真实的杂波协方差矩阵的估计，即式(3)。

式(4)中的检测器具有归一化匹配滤波器的形式，而分母上的归一化因子使得AMF检测器具有恒虚警的特性。文献[7]指出：AMF的检测统计量在H0假设下与真实的杂波协方差矩阵相互独立，是一种恒虚警率检测方法。

然而，在高分辨雷达观测下，绝对均匀的杂波环境几乎不存在，这就意味采用SCM估计真实的杂波协方差矩阵会对检测器的性能造成损失。实测数据显示：高分辨率低视角条件下获得海杂波数据具有空时非平稳性，即海杂波在短的时间内是平稳的，长的时间内是非平稳的；短的距离上是均匀的，长的距离上是非均匀的[15−17]。因此，在非均匀杂波环境中，选取的用于估计杂波协方差矩阵的参考单元数据中可能含有类似目标或者杂波特性明显异于待测单元的单元(统称这样的单元为异常单元)，这就使得SCM出现性能损失，从而影响了AMF检测器的检测结果。

为了避免这种异常单元对估计的杂波协方差矩阵的影响，文献[12,13]均考虑采用删除异常单元的方法，这类方法在一定程度取得相对较好的检测结果，但它们均未考虑在有限参数单元数目时，删除异常单元可能导致矩阵的奇异性的问题。在保持参考单元数目条件下，该文设计了一种基于功率中值和归一化采样协方差矩阵(MNSCM)的估计方法，即

其中，符号Med{·}表示取中值运算，式(5)中的归一化处理去除了杂波纹理分量的影响，很好地抑制了因为各个参考单元数据功率起伏对协方差矩阵的估计性能的影响；与此同时，它又保留了杂波的功率信息，使其能够与自适应匹配滤波检测器相结合。将式(2)中的真实的杂波协方差矩阵替换为式(5)估计的杂波协方差矩阵，得到基于功率中值和归一化采样协方差矩阵的自适应匹配滤波检测器

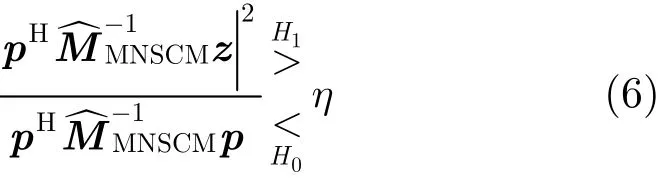
不难证明，与式(4)中的AMF检测器相同，式(6)对应的AMF检测器也是一种恒虚警率检测方法。如果从形式上分析两种自适应检测器，可以看出：在任何类型的杂波环境中，SCM估计器认为每个参考单元对最终估计的杂波协方差矩阵的贡献是均等，即所有的参考单元的对应的权值均为1/K，显然，这种做法只有在均匀杂波环境中才是合理的；而MNSCM估计器在含有功率大的异常单元的杂波环境中，会自适应地赋予那些功率大的异常单元一个较小的权值，这相当于对那些异常单元作相应的惩罚，从而减弱了异常单元对协方差矩阵估计的影响。因此，在含有功率大的异常单元的参考单元中，相比SCM-AMF检测器，MNSCM-AMF检测器会带来更好的检测性能。而对于均匀的杂波环境，MNSCM-AMF检测器与SCM-AMF检测器的形式相同，两种检测器应该具有同等的检测性能。

4 实验结果与性能分析

本节分别采用实测数据和仿真数据对SCM-AMF和MNSCM-AMF的检测性能进行评价。实测数据(1990227_215640_ANTSTEP.mat,VV极化)由(Ice Multi-parameter Imaging X)IPIX雷达[18]于1998在加拿大的安大略湖上采集得到，并且每个距离单元对应的接收数据为一组零均值、单位方差的复序列。表1总结了IPIX雷达参数和所使用数据的详细信息。通过对实验数据作分析可知，杂波数据的幅度分布可以采用不同形状参数的K分布进行描述。图1(a)给出了除了目标单元及其周围4个距离单元以外的其余距离单元采用K分布拟合时对应的形状参数。为了说明K分布的有效性，图1(b)中给出了相应距离单元对应的Kolmogorov-Smirnov (KS) 距离。由图1可知，一方面，K分布能很好地描述杂波的幅度统计特性；另一方面，K分布的形状参数并不是距离单元的常函数，各个距离单元的幅度须用不同形状参数的K分布描述，即杂波呈现非均匀特性。而仿真数据根据实测数据的一阶、二阶统计特性产生，其中，仿真数据幅度服从K分布，其形状参数等于图1(a)中各个距离单元的形状参数的均值；协方差矩阵等于实测数据不同时间段上的协方差矩阵的平均。K分布的形状参数的估计采用经典的矩估计方法，而杂波协方差矩阵利用它与自相关函数的关系，它可以根据式(7)的自相关函数得到。

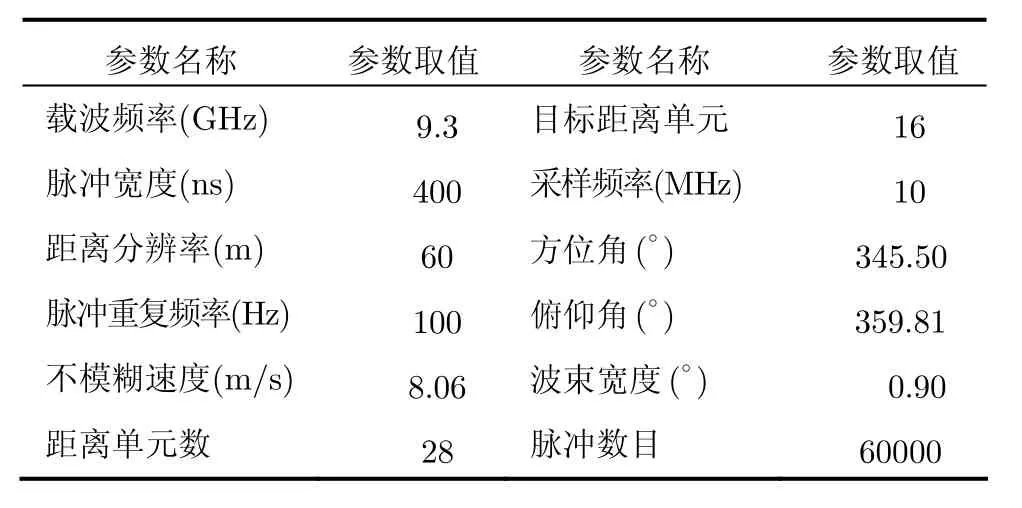
表1 IPIX 雷达参数列表[18]

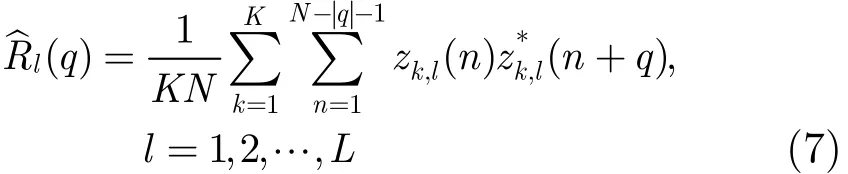
其中，zk,l(n)为第l个时间段上第k个距离单元上回波数据的第n个样本，q是同一距离单元数据中的接收信号的时间差，L由每个距离单元中的脉冲数目除以脉冲累积数N得到，星号“*”表示复数的共轭。

实验中，取虚警概率为1.0e-3，分别添加仿真目标信号到实测数据和仿真数据，观察两种检测器的检测性能，其中，实验门限采用Monte Carlo 方法计算获得。对于实测数据，保留原有的目标信号及其周围4个距离单元数据，而仿真目标添加到其余的距离单元中，这样，对于仿真目标所在距离单元而言，真实目标所在距离单元数据即为异常单元数据。以脉冲累积数N=8为长度，将每个距离单元划分为L=7500的不重合的短向量。每个短向量都会作为H0假设下的待测向量，而同一时间段上的其余距离单元中短向量会被看作是用来估计杂波协方差矩阵的参考单元。因此，用来估计门限的实验次数为7500×28，这等于H0假设下检测统计量数目的总和。将所有的检测统计量按降序重新排列，相应的门限值将是重新排列后的检测统计量的第210个(7500 ×28 × 1.0e-3)。仿真数据采用相同的方法获得虚警概率为1.0e-3时的门限值。

实验中所加仿真目标信号的形式为其中，fd是目标的多普勒频率，初相ϕ是服从区间−[π,π]的均匀分布，a是与传播路径和雷达横截面积有关的常量。定义信号的平均信杂比为

4.1 实测数据条件下两种检测器性能对比

当N=8, K=28，平均信杂比为-5 dB时，两种检测器检测结果如图2所示。由图可知，采用MNSCM的自适应匹配滤波检测器相比传统的自适应匹配滤波检测器具有明显的性能优势。这是因为MNSCM估计方法很好地抑制了参考单元中的异常单元对杂波协方差矩阵估计的影响，从而改善了自适应匹配滤波检测器的检测性能。图3给出了实验所用数据的归一化功率谱与频率之间的关系。

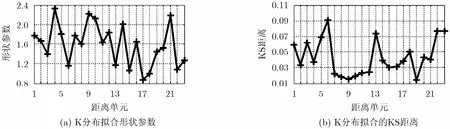
图1 各距离单元K分布拟合形状参数和K分布拟合时的KS距离

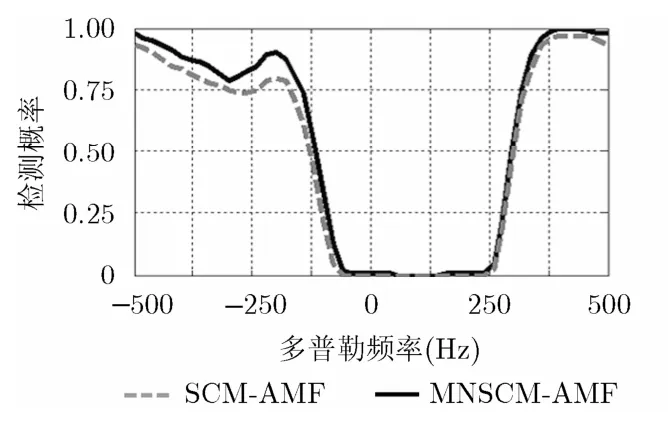
图2 平均信杂比为-5 dB时，MNSCMAMF与SCM-AMF性能对比

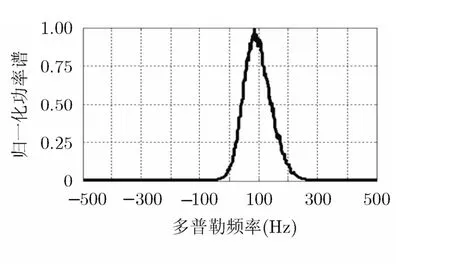
图3 实验所用实测数据的 归一化功率谱

对于指定的多普勒频率处，两种自适应检测器的检测概率随信杂比的变化关系如图4所示。图中给出了3个代表性目标多普勒频率，即频率-200 Hz, 0 Hz 和80 Hz时，两种检测器的检测结果。在这3个频率处，MNSCM-AMF检测器的性能均优于SCM-AMF检测器，而3个频率处的检测性能曲线的差异是因为杂波功率在频域的非均匀分布引起的。由图4可知，当目标多普勒频率靠近功率谱的峰值所在频率时，由于此处杂波的功率密度较大，两种检测器的检测性能相比其他频率处下降了许多。

4.2 仿真数据条件下两种检测器性能对比

为了说明当参考单元中存在功率大的异常样本时，即杂波环境不均匀时，SCM确实会因为估计性能差引起自适应匹配滤波检测器性能损失，而MNSCM能够改善AMF检测器的检测性能。仿真一组大小为40000×28相对均匀的杂波数据，即数据由28个距离单元40000个脉冲组成。选择其中任意一个距离单元作为待测单元，并添加仿真目标到该距离单元，其余的27个距离单元上的数据作为辅助数据。当以N=8为长度作相干检测时，27个距离单元中的数据被划分为135000个短向量，即正常单元的数目。然后，随机地将这27个距离单元中一些正常单元的功率调高，但它依然与距离邻近的其他正常单元共享同一个归一化协方差矩阵。由于这些被调整过的正常单元相比未调整过正常单元具有功率大的特点，这些单元可被看作是异常单元。通过控制异常单元的在原有正常单元中百分比以及异常单元相对正常单元的功率比值，构造一系列不同程度的非均匀杂波环境，观察两种不同协方差矩阵估计方法的自适应检测器在这些环境中的检测性能。

当异常单元相对同一时间段上所有正常单元平均功率的比值固定时(简称功率比)，通过调整异常单元在所有单元中的比例，观察由于异常单元的数目的增加引起的两种检测器之间的性能差异。设平均信杂比为0 dB，当异常单元功率比为5，百分比(即异常单元在所有单元中的比例)依次为5%，15%和20%，图5给了两种检测器的检测结果；当异常单元功率比为20，图6给了两种检测器的检测结果。

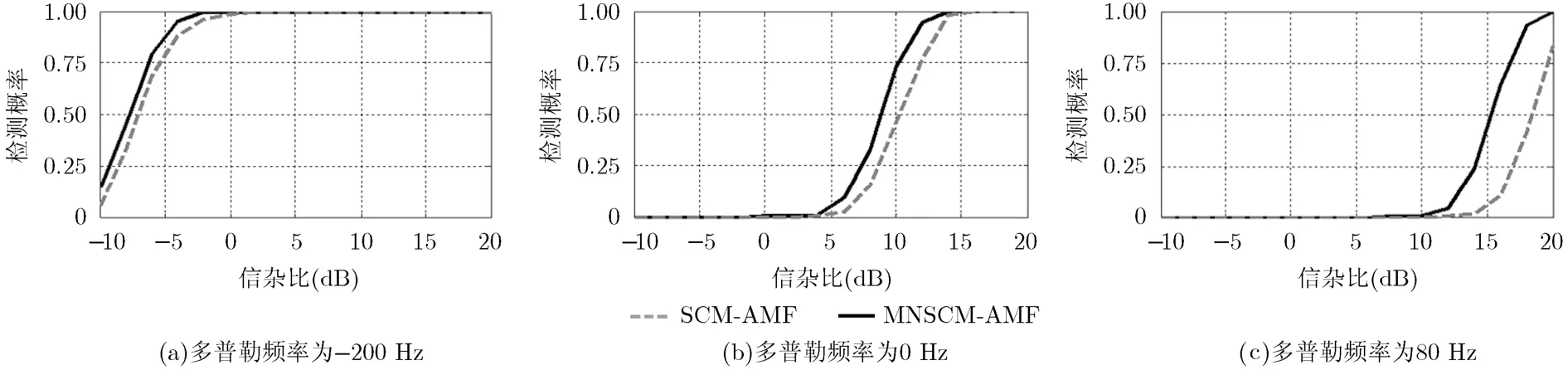
图4 3个频率处，MNSCM-AMF与SCM-AMF性能对比

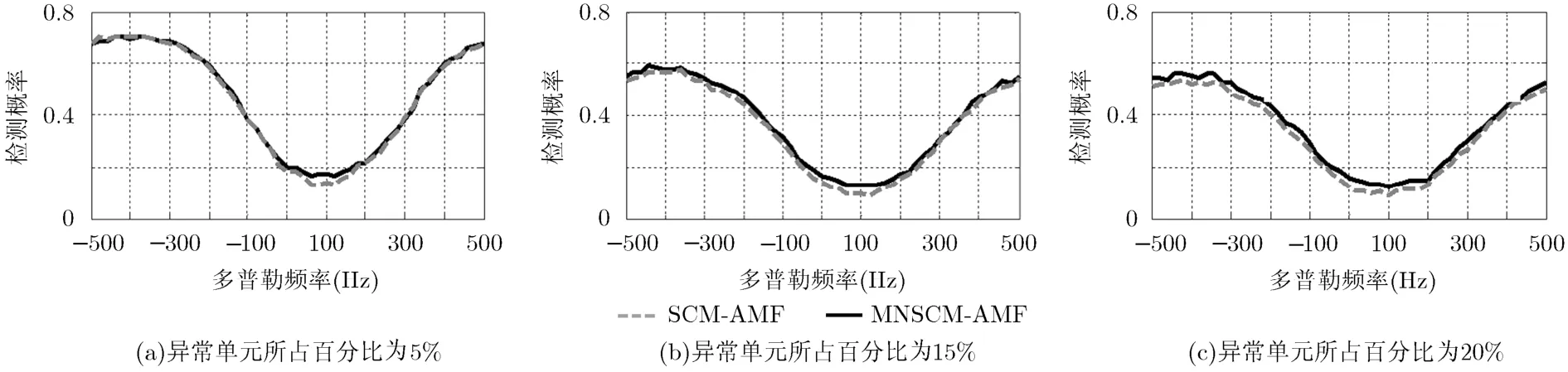
图5 功率比为5, 异常单元所占百分比为5%, 15%和20%时，MNSCM-AMF与SCM-AMF性能对比

图6 功率比为20，异常单元所占百分比为5%, 15%和20%时, MNSCM-AMF与SCM-AMF性能对比

由图5和图6可知，当异常单元数目较少时，MNSCM-AMF检测器相比SCM-AMF检测器的检测性能优势并不明显，二者具有非常相似的检测结果；当异常单元数目增大时，两种检测器的性能出现不同程度的下降，并且异常单元数目越多，两种检测器的性能差异越显著。这是由于异常单元数目的增多不仅会导致两种检测器对应的门限值增大，而且异常单元数目越多，采用SCM方法估计协方差矩阵产生的损失越大。通过对比图5和图6可知，相同异常单元数目条件下，功率比越大，一方面，两种检测器的性能都出现了不同程度的下降趋势，这是由AMF检测器的检测机理决定的。由于AMF检测器的检测统计量与杂波的能量相联系，异常单元功率的增大势必提高了相应的检测门限。另一方面，两种检测器的性能差异越明显，这是因为功率比的增大加剧了杂波的非均匀程度，使得SCM估计方法出现更大性能损失，从而影响了检测器的检测性能。

当多普勒频率为80 Hz，即目标位于强杂波区，异常单元功率比分别设为5和20，异常单元所占的百分比依次为5%, 15%和20%，两种检测器的检测结果如图7和图8所示。由图7和图8可知，功率比增大或异常单元数目增多时，两种检测器的检测曲线右移，即检测性能出现下降。这是因为：在相同数目的异常单元条件下，异常单元功率的增大直接提高了检测门限，从而使得两种检测器的性能呈现下降趋势；而相同功率比条件下，异常单元数目的增大，一方面会增大检测门限，另一方面会引起SCM估计方法更多的估计损失，使得两种检测器的性能差异变得更显著。对于其他多普频率处，具有与上述类似的结果，限于篇幅，这里没有给出详细结果。

5 结束语

本文分析了在高分辨海杂波背景下的动目标检测的两种自适应匹配滤波检测算法，即基于采样协方差矩阵(SCM)和基于功率中值和归一化采样协方差矩阵(MNSCM)的自适应匹配滤波(AMF)检测器。实验结果表明，在非均匀杂波环境中，由于异常单元的存在，SCM的估计性能受阻，限制了传统AMF检测器的检测性能；而MNSCM能很好地抑制异常单元对估计的协方差矩阵的影响，提高了AMF检测器在非均匀杂波环境中的检测能力。

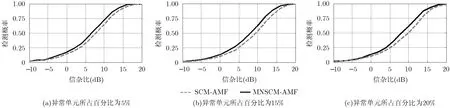
图7 频率为80 Hz，功率比为5，异常单元所占百分比为5%, 15%和20%时，MNSCM-AMF与SCM-AMF性能对比

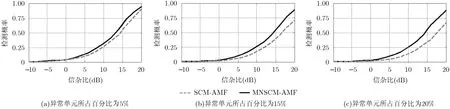
图8 频率为80 Hz，功率比为20，异常单元所占百分比为5%, 15%和20%时，MNSCM-AMF与SCM-AMF性能对比

[1] Javier M C, Javier M G, Alvaro B D C, et al.. Small target detection in high-resolution heterogeneous sea-clutter: an empirical analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 1880-1898.

[2] Chen Xiao-long, Cai Yong, and Cai Fu-qing. Application of the sparse decomposition to micro-motion target detection embedded in sea clutter[C]. Proceedings of the 2013 International Conference on Radar, Adelaide, Canada, 2013:163-166.

[3] Chen Si-jia, Kong Ling-jiang, and Yang Jian-yu. Adaptive detection in compound-Gaussian clutter with partially correlated texture[C]. Proceedings of the 2013 IEEE Radar Conference, Ottawa, Canada, 2013: 1-5.

[4] Chen Xiao-long, Guan Jian, He You, et al.. Detection and extraction of target with micro-motion in spiky sea clutter via short-time fractional fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2), 1002-1018. [5] Maria G, Fulvio G, and Muralidhar R. Statistical analysis of measured polarimetric clutter data at different resolutions [J]. IEE Proceedings-Radar, Sonar and Navigation, 2006, 153(6): 473-481.

[6] Maria G, Fulvio G, Muralidhar R, et al.. Impact of the sea clutter nonstationarity on disturbance covariance matrix estimation and CFAR detector performance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(6): 1502-1513.

[7] Frank R C, Daniel F R, Edward K J, et al.. A CFAR adaptive matched filter detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208-216.

[8] Chan H C, Radar sea-clutter at low grazing angles[J]. IEE Proceedings F Radar and Signal Processing, 1990, 137(2): 102-112.

[9] Ward, K D, Baker, C J, and Watts S. Maritime surveillance radar. part I: radar scattering from the ocean surface[J]. IEE Proceedings, F Radar and Signal Processing, 1990, 137(2): 51-62.

[10] Fulvio G and James H M. Performance analysis of two covariance matrix estimators in compound-Gaussian clutter [J]. IEE Proceedings-Radar, Sonar and Navigation, 1999, 146(3): 133-140.

[11] 张玉石, 许心瑜, 尹雅磊, 等. L波段小擦地角海杂波幅度统计特性研究[J]. 电子与信息学报, 2014, 36(5): 1044-1048. Zhang Yu-shi, Xu Xin-yu, Yin Ya-lei, et al.. Research on amplitude statistics of L-band low grazing angle sea clutter [J]. Journal of Electronics & Information Technology, 2014, 36(5): 1044-1048.

[12] Wei Na. Sea clutter covariance estimation with data-adaptive selection[C]. Proceedings of the IET International Radar Conference, Xi'an, China, 2013: 1-5.

[13] Aghaabdellahian N and Hashemi M M. Improving performance of adaptive detectors in nonhomogeneous environment[C]. Proceedings of the 21st Iranian Conference on Electrical Engineering, Mashhad, Iran, 2013: 1-5.

[14] Moya J C, Menoyo J G, Lopez A A, et al.. Statistical analysis of a high-resolution sea-clutter database[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2024-2037.

[15] Fulvio G and Maria G. Texture modeling, estimation, and validation using measured sea clutter data[J]. IEE Proceedings-Radar, Sonar and Navigation, 2002, 149(3): 115-124.

[16] Maria G, Federica B, and Fulvio G. X-band sea-clutter non-stationarity: influence of long waves[J]. IEEE Journal of Oceanic Engineering, 2004, 28(2): 269-283.

[17] Haykin S. Adaptive Radar Signal Processing[M]. Hoboken, NJ: John Wiley and Sons, Inc., 2007: 159-192.

[18] Cognitive System Laboratory, McMaster University, Canada. The IPIX radar database [OL]. http://soma.mcmaster.ca// ipix.php.2012.10.11.

刘 明： 男，1986年生，博士生，研究方向为海面微弱动目标检测.

水鹏朗： 男，1967年生，博士，教授，研究方向为多速率滤波器理论及应用、图像处理和雷达目标检测.

Adaptive Matched Filter Detector Based on Power Median and Normalized Sample Covariance Matrix

Liu Ming Shui Peng-lang
(National Key Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China)

In nonhomogeneous sea clutter, abnormal cells included reference cells constrain the performance of the Sample Covariance Matrix (SCM), and then influence the detection performance of the traditional Adaptive Matched Filter (AMF) detector, while censoring abnormal cells may cause singularity of the covariance matrix in the case of limited reference cells. Without changing number of the reference cells, this paper devises the median and normalized covariance matrix estimator and uses in the detection scheme of the AMF. Compared with the traditional AMF, the newly devised AMF obtains better performance in both measured and simulated clutter.

Target detection; Sea clutter; Adaptive Matched Filter (AMF); Sample Covariance Matrix (SCM); Median and Normalized Sample Covariance Matrix (MNSCM)

TN957.51

： A

：1009-5896(2015)06-1395-07

10.11999/JEIT140900

2014-07-09收到，2014-10-08改回

国家自然科学基金(61271295)资助课题

*通信作者：刘明 mingliu1608@163.com