一种用于RaptorQ码的降维快速译码算法
2015-07-12晓张更新徐任晖牛大伟
郭 晓张更新 徐任晖 牛大伟
(解放军理工大学通信工程学院 南京 210007)
一种用于RaptorQ码的降维快速译码算法
郭 晓*张更新 徐任晖 牛大伟
(解放军理工大学通信工程学院 南京 210007)
针对新型高效数字喷泉码——RaptorQ码译码复杂度高的问题,利用它是系统码的特性,该文提出一种降维快速译码算法。该算法利用预先计算的逆矩阵,将译码过程中对接收编码约束矩阵的求逆转化为对更小维数矩阵的求逆,以降低译码复杂度。算法译码效果与现有译码算法等价。仿真结果表明,在信道符号删除概率较低(小于0.2)时,该算法的译码速度显著高于现有算法。
译码算法;数字喷泉;RaptorQ码;降维译码
1 引言
RaptorQ码[1]是数字喷泉技术的最新研究成果,目前被广泛应用于无线实时多媒体传输、文件分发、卫星通信等诸多领域[2−6]。文献[7]的研究结果表明,在分组长度小于104量级时,仅仅通过引入两个冗余符号,RaptorQ码即可将译码失败概率降至10−6量级;与LT(Luby-Transform)码和Raptor码相比,RaptorQ码为实现成功译码所需的冗余分组数大为降低。
然而,RaptorQ码的性能提升是以编译码复杂度的提高为代价的。理论上,使用置信传播(Belief Propagation, BP)译码算法可在线性时间复杂度内对Raptor类码(包括RaptorQ码)进行译码[8]。但在实践中,受码长度的限制,单纯使用BP译码算法会使成功译码概率大大降低。为了实现在较少编码冗余的情况下提高成功译码的概率,当前实用的译码算法主要依赖于对接收编码约束矩阵A'的求逆运算[9]。文献[10]的研究表明,在符号长度T=4的情况下,求逆运算所耗费的时间约占整个编译码时间的99%; T=1024时,这一时间约占整个编译码时间的95%。可见,RaptorQ码的译码复杂度由矩阵求逆运算的复杂度决定。
目前,针对RaptorQ码编译码过程中求逆运算复杂度较高的问题,IETF RFC 6330[1]利用码约束矩阵具有稀疏性的特点,采用失活译码(Inactivation Decoding, ID)技术和高斯消元(Gaussian Elimination, GE)法,给出了一种有效的RaptorQ码译码算法,称为失活译码高斯消元(Inactivation Decoding Gaussian Elimination, IDGE)算法。文献[10]在此基础上提出了优化失活译码高斯消元(Optimized Inactivation Decoding Gaussian Elimination, OIDGE)算法,该算法通过简化译码步骤和对行选择方法进行优化,提高了译码计算的效率。文献[11]等利用GPU的并行结构,给出了RaptorQ码的并行译码算法。文献[12]利用Sherman-Morrison公式和预先计算的逆矩阵,给出了一种递归译码算法,该算法在信道符号删除概率较低时,相对于前述算法性能有较大提升。本文称该算法为递归逆矩阵译码(Recursive Matrix Inversion Decoding, RMID)算法。但该算法需要获得信道的先验符号删除概率,计算效率的提升依赖于对信道符号删除概率估计的准确性,有一定的应用局限性。
为了进一步降低译码复杂度,本文利用RaptorQ是系统码的特性,提出一种降维快速译码(Dimensionality Reduced Fast Decoding, DRFD)算法。该算法利用预先计算的逆矩阵,将译码过程中对接收编码约束矩阵A'的求逆转化为对更小维数矩阵A''的求逆,以降低译码复杂度。算法使用的降维变换方法未改变接收端编码约束矩阵的符号间约束关系,译码效果与现有译码算法等价。
2 RaptorQ码编译码原理与译码复杂性分析
RaptorQ可以看作一种无限码长的线性分组码,其编译码过程可由生成矩阵来表示,如图1所示。

图1 RaptorQ码编译码原理框图
编码过程分为预编码和LT(Luby-Transform )编码[13]两个步骤,预编码器首先将K个源符号编码成L个中间符号,LT编码器再将L个中间符号编码成无限长码序列。RaptorQ码的编译码运算是在GF(256)上实现的,基本的运算单位为Byte(8 bit),为了提高编译码效率,通常将同时参与运算的若干个Byte视为一个符号。符号大小(即每个符号包含的字节个数)为T, IETF RFC6330推荐的取值范围为4至1024。具体编码过程如下。在预编码阶段,K个源符号构成的向量经过尾部补零操作后形成长度为K'的向量t',K'为RaptorQ码预置的源符号向量长度,K'≥K。t'再经过首部补足S+H个零后形成输入向量d=(d0,d1,…, dL−1)T, S为预编码矩阵A中LDPC(Low Density Check Codes)约束的个数,H为HDPC(High Density Check Codes)约束的个数,L=K'+S +H 。经过预编码器后生成中间符号向量c=(c0,c1,…,cL−1)T,输入向量和中间符号向量的关系为

预编码矩阵A由一系列子矩阵构成。
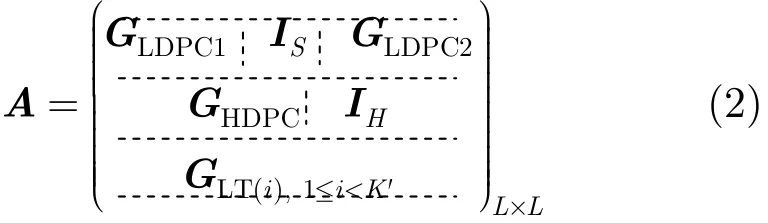
其中,IS为S×S维单位阵,IH为H×H维单位阵,GLDPC1和GLDPC2为行数S的LDPC矩阵,GHDPC为H×(L−H)维HDPC矩阵,GLT(i),1≤i<K′为K'×L维的LT约束矩阵,i为内部符号标识(Internal Symbol Identifier, ISI), RaptorQ码可通过ISI唯一确定编码符号的LT约束关系,详见文献[1]。
在LT编码阶段,中间符号向量c经过LT编码器生成无限长编码符号向量e=(e,e,…,e,…)T。
01K−1其中由K'−K个补零符号所生成的编码符号恒为零,接收端译码器可根据编码器参数进行重现,不需要进行传输。其余的符号用非负整数编号,即
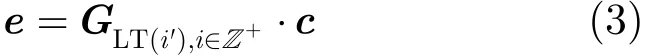
ℤ+为非负整数集,i'为编码符号标识(Encoding Symbol Identifier, ESI)。
在编码过程中,为了保证RaptorQ的系统码特性,预编码和LT编码使用了K个相同的LT约束关系,由

可知,LT编码器生成的前K个编码符号即为K个源符号。在生成的无限长码编码序列中,除去K个源符号的编码符号称为修复符号。
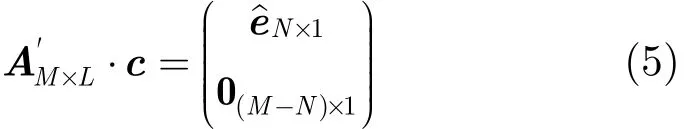
得到。若A'不可逆,方程组不具有唯一解,译码失败,需要接收更多的编码符号e',直至A'可逆。第2步,由式(3)可得向量t',去掉补足的零后即可得源符号向量t,从而完成译码过程。需要指出的是,本文所指的矩阵可逆是指矩阵的列满秩,即可以通过初等矩阵行变换将其上三角化。
从上述编译码过程可以看出,RaptorQ码的编译码算法都依赖于对约束矩阵的求逆运算。在发送端,对于给定的编码长度K,预编码约束矩阵A是固定的,其逆矩阵−1A可以通过预先计算的方式得到。在接收端,由于传输过程中符号丢失具有随机性,每一次参与译码运算的A'是不同的,译码过程不可避免地需要对A'进行求逆运算。一般的矩阵求逆算法,如GE算法,具有O(N3)的计算复杂度。为了提高译码的效率,现有的译码算法[1,10,12]利用A'具有稀疏性的特征,主要采用失活译码技术加快译码速度。在失活译码的过程中,每个迭代译码步骤都需要优先选择矩阵中非零元最少的行优先进行译码。该操作需要对矩阵元素进行扫描,占用大量的译码时间,在矩阵维数较高时,算法相当低效。综上所述,对高维矩阵的操作是现有译码算法效率不高的主要原因。
3 降维快速译码(DRFD)算法设计
3.1 DRFD算法设计的出发点
在第2节介绍的两步译码过程中,首先需要求解式(5)恢复出L个中间符号,也就是求解一个包含M个线性约束关系和L个未知变量的线性方程组,该计算过程等价于对一个M×L维矩阵进行求逆操作。观察进入RaptorQ码译码器输入端的接收符号向量, K个源符号经过删除信道后,接收端收到其中的s个,其余为r个修复符号,s+r=N,译码器仅需要译出另外K−s个源符号即可得到源符号向量t。RaptorQ码的编译码过程都是线性运算,理论上,对一个包含r(r≥K−s)个线性约束关系和K−s个未知变量的线性方程组求解,即有可能得到K−s个未知变量,等价于对r×(K−s)维矩阵进行求逆操作。
RaptorQ码具有极高的码率特性,其译码失败的概率为[14]

由此可以看出,成功译码所需的编码符号数N以很高的概率等于参与编码符号个数K,即当修复符号的个数r约等于丢失符号的个数K−s时,译码即可以很高的概率成功译码。编码符号经过符号删除概率为p的删除信道后,丢失的源符号数量K−s≈K⋅p。当信道符号删除率p≪1时,K⋅p≪K ,可得r≈K−s≈K⋅p≪K<L≤M。从这个数量关系看,在信道的符号删除概率较低时,第2节所述的两步译码方法是低效的。如果存在一种有效的方法将译码矩阵从M×L维降为r× (K−s)维,RaptorQ码译码即可转化为对较小维数矩阵求逆的过程,从而提高译码速度。
3.2 降维变换
DRFD算法利用预先计算的编码矩阵的逆−1A来实现接收端编码约束矩阵的降维变换。采用DRFD算法的译码器结构如图2所示。

图2 使用DRFD算法的RaptorQ码译码器结构
降维变换的原理可以用向量分解的方法进行说明。将含补零符号的待求的译码向量dˆ分解成两个向量之和:

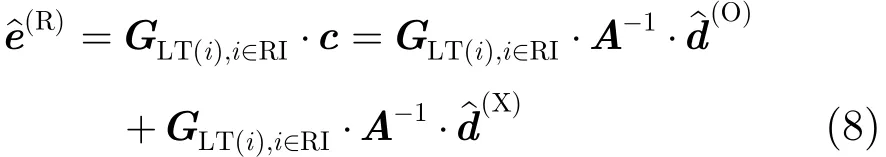
其中GLT(i),i∈RI为修复符号对应的LT约束关系矩阵,RI为修复符号对应的ESI集合。对于给定的编码长度K,依据文献[1]给出的RaptorQ码编码构造方法,编码约束矩阵的逆矩阵−1A可以通过预先计算得到。
式(8)可以化简为

给出下面的定理,该定理为降维变换提供理论依据。
定理1 对于RaptorQ码的译码,式(9)有唯一解,当且仅当式(5)有唯一解。
证明 RaptorQ码的设计保证了预编码矩阵AL×L是可逆的,即其所有L个行是线性无关的。在接收编码约束矩阵×L中,s个源符号、S个LDPC约束关系、H个HDPC约束关系、K'−K个补零约束关系所对应的行与AL×L相同,因此这些行也构成线性无关组。
×L中的s+S+H+(K'−K)个线性无关的行,剩余矩阵的秩为L−(s+S+H+(K'−K))=K−s ,即rank(GLT(i),i∈RI)=K−s 。A−1为满秩矩阵,由A''=GLT(i),i∈RI⋅A−1可知rank(A'')= rank(GLT(i),i∈RI)=K−s ,故式(9)有唯一解。
定理1说明,降维变换并没有改变接收编码符号的可译特性。式(9)使用了与式(5)相同的编码约束关系,即降维译码方法与传统的两步译码方法译码效果等价。
3.3 DRFD算法
如第2节所述,传统RaptorQ码的译码算法依赖于对接收编码约束矩阵A'进行求逆,在能够进行成功译码的前提下,A'的维数仅取决于编码器的参数K,不受信道删除率的影响。而DRFD算法则依赖于对降维矩阵A''的求逆,A''的维数受信道删除率的影响。当信道符号删除率p≪1时,A''相对于式(5)中的A',维数大大降低。
以K=10为例,根据文献[1]给出的RaptorQ码编码构造方法,编码器向信道发送11个编码符号。假设信道分组删除率约为0.1,接收端接收到9个源符号和1个修复符号,加入编码约束关系后,接收端编码约束矩阵为。现有的GE算法、×27IDGE算法和OIDGE算法都需要对这个27×27维矩阵执行求逆运算,以恢复出27个中间符号。RMID算法虽然不直接对A'进行求逆,但在递归求逆的过程中,使用到的中间矩阵维数仍然是27×27维的。利用本文所提算法,经过降维变换后,A''为1×1维矩阵,直接可以计算出丢失的源符号。
经过降维变换后,解式(9)即可得到丢失的源符号。丢失的源符号与接收到的源符号合并,即可得到完整的译码向量dˆ。
对式(9)通常使用高斯消元法求解,若高斯消元成功,即可完成译码过程;若高斯消元法失败,则需要接收更多的修复符号以完成译码过程。在需要多次译码情况下,可以采用文献[15]提出的渐增译码算法,以减少重复执行高斯消元法需要的计算开销。
表1给出DRFD算法的步骤。

表1 DRFD算法
从表1给出的DRFD算法可译看出,该算法改变了传统的两步译码结构,不再需要先译出中间符号而后译出源符号,而是直接通过接收的编码符号译出丢失的源符号。
在执行DRFD算法之前,译码需要等待接收N个编码符号。由于RaptorQ码的高可译特性,通常取N=K+2。采用此取值可将译码失败的概率降到10−6量级,同时引入的解码时延和计算开销都比较小。译码器在收到编码符号的同时,可以通过某种同步方式获得每个符号的编码符号标识ESI(如将ESI同编码符号一同发送至接收端)。译码器通过ESI可识别接收到的源符号和修复符号,这些作为算法参数输入至DRFD算法。
修复符号的LT约束关系由修复符号的ESI唯一确定,算法步骤1的实现方法详见文献[1]。矩阵GLT(i)为二进制稀疏矩阵,算法步骤2利用的该特征将矩阵乘法运算转化成矩阵的行累加运算,其中为A''的第i行,为A−1的第k行。算法步骤3中,为L维向量,但部分元素为零,在计算矩阵乘法时,A''中部分列不参与运算,可以节约一些计算开销。算法步骤4中,为L维向量,但仅包含K−s个未知源符号,其余元素为零,因此A''中仅有未知符号对应的K−s个列参与的生成,A''可以看作r×(K−s)维矩阵。
算法中所有的加法和乘法运算都是GF(256)上的运算。算法步骤2中使用到预编码约束矩阵A的逆矩阵A−1,该矩阵预先计算后存储在译码器端,在译码过程中,其计算开销可以忽略不计,但增加了译码器端的存储开销。
3.4 计算复杂度分析
DRFD算法使用降维变换降低执行GE算法的矩阵的维数,以达到降低译码计算复杂度的目标。作为降维的代价,计算A''和e(R)的过程需要引入额外的矩阵乘法和加法,在一定程度上增加了计算量。但GLT(i),i∈RI为二进制稀疏矩阵,利用算法中步骤2给出计算方法,对A−1中的行进行异或操作即可计算出A'',不需要进行GF(256)上的矩阵乘法。若信道的符号删除率为p,则矩阵GLT(i),i∈RI的行数r约为pK, DRFD算法中步骤2计算A''的译码计算复杂度为O(pKL),L为中间符号的个数,略大于K。中约有(1−p)K个非零元,矩阵A''的行数约为pK, DRFD算法中步骤3计算的译码计算复杂度为O(p(1−p)K2)。算法步骤4在矩阵A''上执行GE算法,计算复杂度O(p3K3)。因此DRFD算法整体的计算复杂度为O(p3K3)。
另外,求解式(9)可直接得到未知符号,不再需要利用矩阵乘法操作从中间符号c来恢复未知符号。在信道的符号删除率为p较小的情况下,相对于具有O(N3)计算复杂度的GE消元法,DRFD算法可以大大减小计算开销。
4 仿真结果及分析
为了验证DRFD算法的性能,本节利用仿真实验将其与GE, IDGE, OIDGE和RMID算法进行比较。IDGE算法参照文献[1]实现,OIDGE算法参照文献[10]实现,GF(256)上的乘法运算采用查表法实现。仿真中所采用的信道为符号删除信道,且具有稳定的符号删除概率p。参与RaptorQ编码的源符号个数K的取值范围为10到2000,符号大小T取值分别为4和128,符号删除概率p取值为0.01, 0.10和0.20,对于每个(K,T,p)三元组进行500次实验,每次实验使用相同的编码数据,分别使用5种不同的译码算法进行译码。仿真算法采用C语言实现,仿真程序在同一台PC机(Intel i3 CPU@2.4G, DDR2@400MHz)上运行。
由于RaptorQ码的可译特性由码结构本身决定,上述5种译码算法具有相同的可译性能,本文主要对译码算法的计算复杂度进行比较,不对译码失败概率进行比较。各译码算法在实现过程中使用微秒精度的时间计数器,译码计算复杂度取译码时间的平均值作为仿真结果。
在给定分组个数K和符号大小T的条件下,由于RMID算法需要预先对信道符号删除概率进行估计,且算法性能受信道符号删除率和估计准确性两个因素的影响,本文所提的DRFD算法的性能仅受信道符号删除率影响,GE, IDGE, OIDGE算法的性能则跟这两个因素无关。为了清楚说明各算法性能之间的关系,下文分两部分进行分析。
4.1 与GE, IDGE和OIDGE算法的比较
图3(a)给出了在符号长度T=4时,译码时间随源分组个数K的变化曲线。GE, IDGE, OIDGE算法的译码时间仅受分组个数K和符号大小T影响,在图中分别给出一条曲线。
由图3(a)可以看出,RFC6330给出的IDGE算法译码速度较GE算法和OIDGE算法低,原因是IDGE算法采用了较为复杂的行选择算法,该算法虽然可以最大可能地利用接收编码约束矩阵A'的稀疏特性,但需要对A'的元素进行多次扫描,扫描矩阵元素需要消耗大量的计算时间;在K较小时,GE算法的译码速度略优于OIDGE算法,随着K的不断增加,OIDGE算法的译码速度显著优于GE算法。上述结果与文献[10]的结论一致。DRFD算法译码速度在符号删除概率p较低时,译码性能显著优于上述3种算法,例如在p=0.1时,对应于K为100, 500和1500, DRFD算法的译码速度是OIDGE算法的17.4, 12.7和7.3倍。随着p的增长,DRFD算法的译码速度随之降低。这是由于随着p的增长,参与DRFD算法译码的修复分组个数随之增加,导致译码矩阵A''的规模随之增长,在A''上执行高斯消元算法的算法复杂度为O(N3),从而增加了算法中步骤4的译码时间。
图3(b)给出了在T=128时的仿真结果。与图3(a)的结果类似,在符号删除概率p较小时,DRFD算法的译码速度同样优于现有3种译码算法,例如在p=0.1时,对应于K为100, 500和1500, DRFD算法的译码速度是OIDGE算法的5.3, 2.7和2.1倍,但相对于T=4时效率的提高有所减小。T增大导致DRFD算法译码速度降低的主要原因是,在算法的步骤3中,T增大将导致矩阵乘法的计算量增加,从而使步骤3占用大量的计算时间。
从图3(a)和图3(b)可以看出,随着p和K的增加,DRFD算法的译码速度的优势会逐步降低。在p=0.2, K=2000时,DRFD算法的性能接近OIDGE算法。表明DRFD算法的应用有一定的局限性,即DRFD算法不适用于高误码率和分组块较大的应用场景。K=2000, T=128时,单个传输的数据分段大小为256k Byte。单个传输分段大小小于256k Byte、信道符号删除概率p小于0.20,这些限制对于当前大多数的多媒体应用来说是可满足的[16]。
4.2 与RMID算法的比较
图4给出了DRFD算法与RMID算法在T=4时,p=0.01和p=0.20的仿真结果。由于RMID算法需要预先估计信道符号丢失率,故给出两条曲线,分别表示能够准确预先估计信道质量和估计的信道质量有误差时的情况。pˆ表示预先估计的信道符号丢失率。从图上可以看出,在给定的信道符号丢失率的情况下,对信道质量的估计值影响RMID算法的性能,估计值的误差会降低RMID算法的译码速度,这与文献[12]的结论一致。DRFD算法不需要预先估计信道符号丢失率,故给出一条曲线。在两种信道符号丢失率的情况下,DRFD算法的译码速度均优于RMID算法。
在T=128时,DRFD算法与RMID算法的对比仿真结论与上述仿真结论类似,本文不再赘述。
5 结束语
RaptorQ码是一种高效的数字喷泉码,但由于译码运算需要对较高维数的接收端编码约束矩阵进行求逆运算,其译码的计算复杂度较高。本文利用预先计算的逆矩阵,提出了一种降维快速译码(DRFD)算法,该算法译码结果和现有译码算法等价,不改变现有算法对RaptorQ码的可译性,在信道的符号删除概率p较低(小于0.2)时,译码速度显著优于现有算法。信道的符号删除率越低,DRFD算法的性能提升约明显。该算法的性能虽然受信道符号删除率的影响,但不需要预先得到信道符号删除率的先验信息,相对于RMID算法,在提高译码速度的同时,提升了算法的可用性。
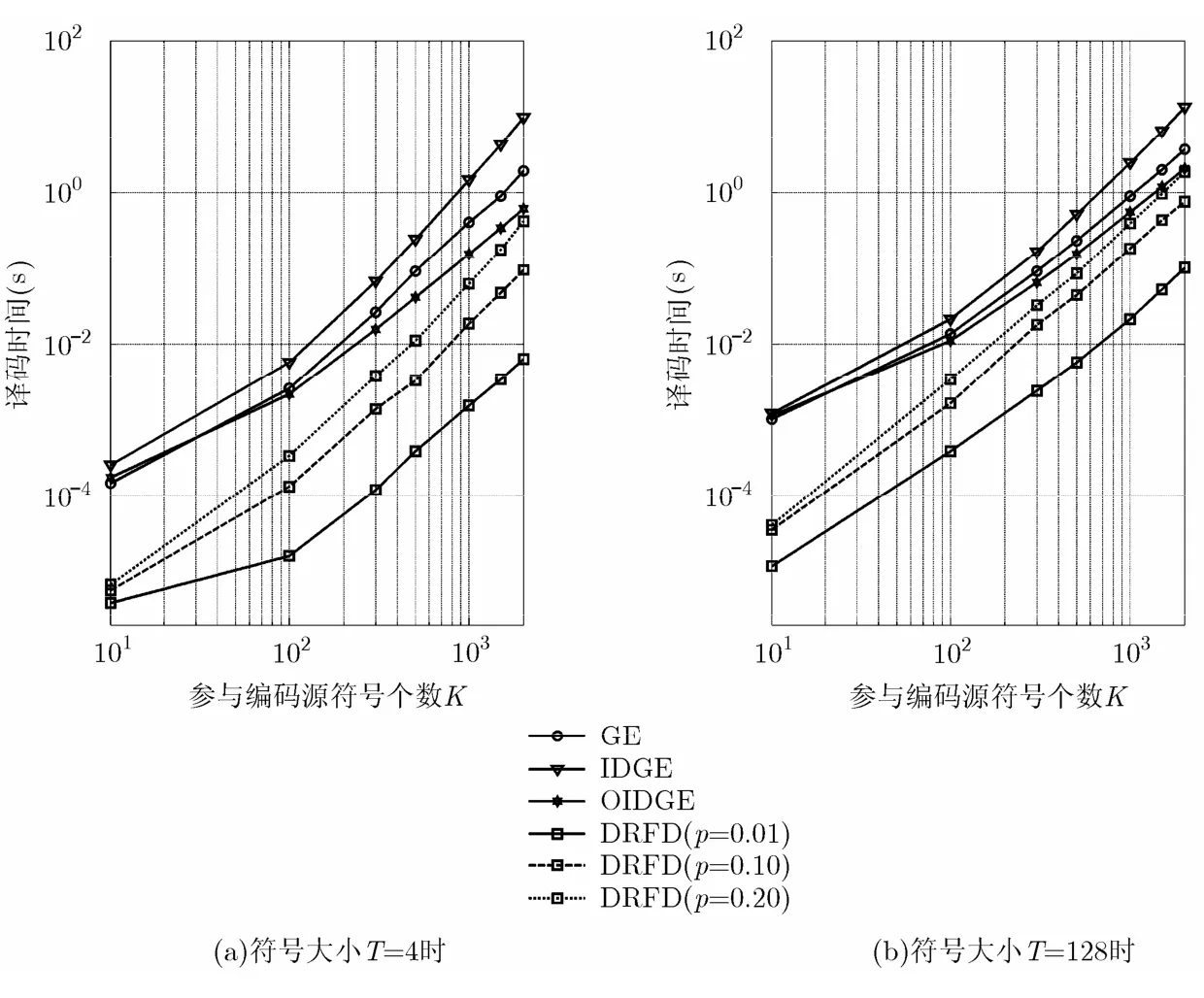
图3 DRFD算法在不同符号删除率下与GE, IDGE和OIDGE算法性能比较
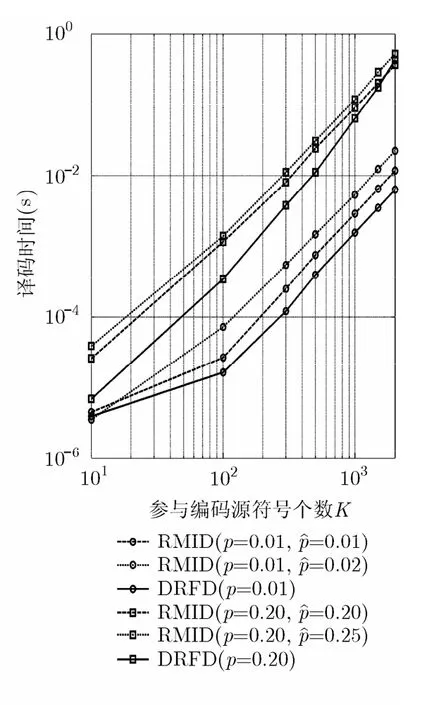
图4 T=4时DRFD算法在不同符 号删除率下与RMID算法性能比较
[1] IETF RFC 6330. RaptorQ forward error correction scheme for object delivery[S]. IETF Proposed Standard, 2011.
[2] Calabuig J, Monserrat J F, Gozálvez D, et al.. AL-FEC for streaming services in LTE E-MBMS[J]. EURASIP Journal on Wireless Communications and Networking, 2013, 2013(1): 1-12.
[3] Bouras C, Kanakis N, Kokkinos V, et al.. Embracing RaptorQ FEC in 3GPP multicast services[J]. Wireless Networks, 2013, 19(5): 1023-1035.
[4] Bouras C, Kanakis N, Kokkinos V, et al.. Application layer forward error correction for multicast streaming over LTE networks[J]. International Journal of Communication Systems, 2013, 26(11): 1459-1474.
[5] Pandya M A U, Trapasiya S D, and Chinnam S S. Implementation of AL-FEC RaptorQ code over 3GPP E-MBMS network[J]. International Journal of EngineeringResearch and Technology, 2013, 2(5): 170-177.
[6] 黄晓可, 刘洛琨, 张剑, 等. RaptorQ 码级联方案在卫星通信中的应用[J]. 信息工程大学学报, 2013, 14(3): 306-311.
Huang Xiao-ke, Liu Luo-kun, Zhang Jian, et al.. Application of the RaptorQ codes concatenation in satellite communications[J]. Journal of Information Engineering University, 2013, 14(3): 306-311.
[7] Shokrollahi A and Luby M. Raptor codes[J]. Foundations and Trends in Communications and Information Theory, 2011, 6(3/4): 213-322.
[8] Shokrollahi A. Raptor codes[J]. IEEE Transactions on Information Theory, 2006, 52(6): 2551-2567.
[9] Kim S, Lee S, and Chung S Y. An efficient algorithm for ML decoding of Raptor codes over the binary erasure channel[J]. IEEE Communications Letters, 2008, 12(8): 578-580.
[10] Mladenov T, Nooshabadi S, Kim K. Efficient GF (256) raptor code decoding for multimedia broadcast/multicast services and consumer terminals[J]. IEEE Transactions on Consumer Electronics, 2012, 58(2): 356-363.
[11] Hu L, Nooshabadi S, and Mladenov T. Forward error correction with Raptor GF(2) and GF(256) codes on GPU[J]. IEEE Transactions on Consumer Electronics, 2013, 59(1): 273-280.
[12] Lu Y, Lai I, Lee C, et al.. Low-complexity decoding for RaptorQ codes using a recursive matrix inversion formula[J]. IEEE Wireless Communications Letters, 2014, 3(2): 217-220.
[13] Luby M. LT codes[C]. Proceeding of the 43rd Annual IEEE Symposium on the Foundations of Computer Science, Vancouver, Canada, 2002: 271-280.
[14] 3GPP Tdoc S4-110449. Rationale for MBMS AL-FEC Enhancements[R]. 3rd Generation Partnership Project (3GPP), 2011.
[15] Kim S, Ko K, and Chung S Y. Incremental Gaussian elimination decoding of raptor codes over BEC[J]. IEEE Communications Letters, 2008, 12(4): 307-309.
[16] Mladenov T, Nooshabadi S, and Kim K. MBMS raptor codes design trade-offs for IPTV[J]. IEEE Transactions on Consumer Electronics, 2010, 56(3): 1264-1269.
郭 晓: 男,1981年生,讲师,博士生,研究方向为信道编码、深空通信、无线网络.
张更新: 男,1967年生,教授,博士,博士生导师,研究方向为卫星通信、深空通信.
徐任晖: 男,1978年生,讲师,博士,研究方向为认知无线电.
牛大伟: 男,1978年生,讲师,博士,研究方向为无线网络、光交换网络.
Fast Decoding Algorithm for RaptorQ Code Using Matrix Dimensionality Reduction
Guo Xiao Zhang Geng-xin Xu Ren-hui Niu Da-wei
(Institute of Communications Engineering, PLA University of Science and Technology, Nanjing 210007, China)
RaptorQ code is a novel and efficient digital fountain code and its decoder is known to be too complicated. Considering the characteristic of the systematic code, a very fast decoding algorithm can be performed using matrix dimensionality reduction. The algorithm exploits a pre-calculated inverse matrix to achieve dimensionality reduction for the
code constraint matrix. As a result, the decoding complexity is reduced significantly while the failure-overhead curve is still identical to that of the conventional approaches. The simulations show that the decoding speed of the proposed algorithm outperforms the state-of-the-art algorithms, when the erasure probability of the channel is relatively low (less than 0.2).
Decoding algorithm; Digital fountain; RaptorQ code; Dimensionality reduction decoding
TN911.22
: A
:1009-5896(2015)06-1310-07
10.11999/JEIT141037
2014-08-04收到,2014-10-31改回
国家自然科学基金(91338201, 61032004)资助课题
*通信作者:郭晓 gosiuua@163.com
