方程式赛车车架建模与模态分析

张宝玉，李萍

（江苏食品药品职业技术学院机电工程系，江苏 淮安 223001）

方程式赛车车架建模与模态分析

张宝玉，李萍

（江苏食品药品职业技术学院机电工程系，江苏 淮安 223001）

大学生方程式赛车车架的模态分析对于减少整车振动和提高动态性能具有重要意义。在CATIA软件中建立方程式赛车车架几何模型，将其导入有限元软件HyperMesh中进行网格划分、加载和边界处理，对车架进行自由模态分析。通过Optistruct计算，得到车架各阶固有频率与振型，进而分析该车架结构发生共振的可能性。

赛车车架；有限元；模态分析；共振

CLC NO.:U463.8 Document Code: B Article ID: 1671-7988(2015)05-70-03

引言

不同于普通汽车，方程式赛车车架作为各系统总成的承载体，承受着不同工况下的载荷。加之于赛车在比赛中行驶速度快，工作强度大等因素，因此，车架结构对赛车性能有很大影响，直接关系比赛成绩的好坏。本文运用三维建模和有限元软件分别对车架建立三维和有限元模型，通过模态分析获得车架各阶固有频率和振型，使其满足震动要求，避免由共振带来的破坏，保证赛车可靠性和安全性。

1、车架模型建立

1.1 车架几何模型

CATIA建模软件具有强大的几何生成与修改功能，通过扫掠、布尔操作等功能可以对多个交叉杆件进行有效地处理。依据中国大学生方程式汽车大赛规则[1]对车架的技术要求，为了减小在车架几何清理和网格划分时花费的时间和强度，本文直接在 CATIA环境中中扫掠杆件中面并对相贯处进行修剪整理，这样既得到了整个车架的实体模型，并将其软件格式接口设置为STEP，保证导入HyperMesh有较好的几何要素。图1为所建立的车架几何模型。

1.2 车架有限元模型建立

从广义上讲，有限元模型包括单元、节点、材料特性、实常数、边界条件以及其他反应系统结构的特性参数。车架有限元模型的建立是分析和改进车架结构的关键步骤，如果有限元模型的建立不够准确，或是与实际结构相差很大，这样都会给计算结果带来影响。车架有限元模型建立流程如图2所示。

1.2.1 材料属性

车架选用的材料为高强度铬钼合金钢，它具有良好延展性与强度，采用氩弧焊接法。其特性如表1所示。

表1 车架材料属性Lab.1 Frame material properties

1.2.2 网格划分

有限元计算是基于单元和节点进行的，而二者是由网格划分产生的，因此，网格质量的好坏直接影响计算结果与分析的精确度。HyperMesh是一个网格划分非常智能的有限元前处理软件，通过网格自动划分技术能生成密度均匀、质量较高的网格模型。

研究车架是由不同外径与壁厚且具有一定空间结构与几何尺寸的圆管焊接而成。为了节省建模时间，在前述中，已经建立了圆管的中面，在 HyperMesh里只需通过 Geom cleanup和surf edit 等操作进行几何清理，接下来就要对清理完的车架进行网格划分，考虑到驾驶舱与发动机舱处相交杆及其他关键杆件受力复杂，在相交处划分较密网格，其余杆受力相对简单，为了满足有限元模型的计算精度，保证计算结果的准确性，车架有限元模型采用板壳单元进行网格划分。相交处尽量多划分tria3单元，在非交叉处划分均匀的quad4单元。总之，应该保证划分的网格既要疏密适当，又要均匀过度。整个车架模型单元尺寸为4mm，划分单元201102个，节点200234个，tria3单元占9%，车架有限元模型见图3所示，图4为局部网格图。

2、模态分析理论

模态是结构的一种固有的振动特性，模态分析是研究结构动态特性的一种近代分析方法，是系统辨别方法在工程振动领域中的应用[2]。通常，结构的动态特性用模态参数（模态频率、模态振型、模态阻尼）描述；通过对结构的模态分析求得这些动态特性参数。

由振动理论可知，系统的运动微分方程：

其中：M、C、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵；x(t)、x˙(t)、˙x˙(t)分别为系统的位移矢量、速度矢量和加速度矢量；P(t)为激振力列阵。由于车架振动系统阻尼C很小，可以忽略其影响，且采用自由振动方式建立模态模型，即P(t)=0，所以上式简化为：

由式（2）可推导出多自由度系统的固有频率和主振型方程

其中，A为主振型，ω为系统固有频率；ω2为特征值。保证式（3）有意义，则

式（4）说明n自由度系统有n个特征值，即系统有n个固有频率。

模态分析就是基于该理论通过，有限元计算得到系统振动的特征值问题，即求得振动系统特征方程的根即固有频率和模态振型。

3、车架模态计算及结果分析

车架的模态分析是为了避免车架振动产生的疲劳损坏，提高车架结构疲劳强度。进行模态分析时，由于所要求解的结果是车架结构的固有频率及固有振型，与所受外力无关，故可忽略外部载荷的作用，即对车架进行自由模态分析[3]。

汽车在路面行驶，由路面不平引起的激振频率为1~12Hz；由车轮不平衡引起的激振频率一般在11Hz左右[4]；由发动机工作引起的激振频率计算公式如下：

其中：n为发动机转速；z为发动机气缸数；τ为发动机冲程数，赛车选用CBR600四缸发动机，经调校怠速转速为3000r/min，代入上式计算得发动机激振频率为100Hz。

车架设计要求车架结构的各阶固有频率能够有效避开赛车由于上述三个因素引起的激振频率，从而避免发生共振现象。

在已建立的车架有限元模型基础上运用 HyperMesh/ OptiStruct求解器采用分块 Lanczos法对车架进行自由模态分析，得到前六阶车架固有频率和振型见表2。图5为分析结果。

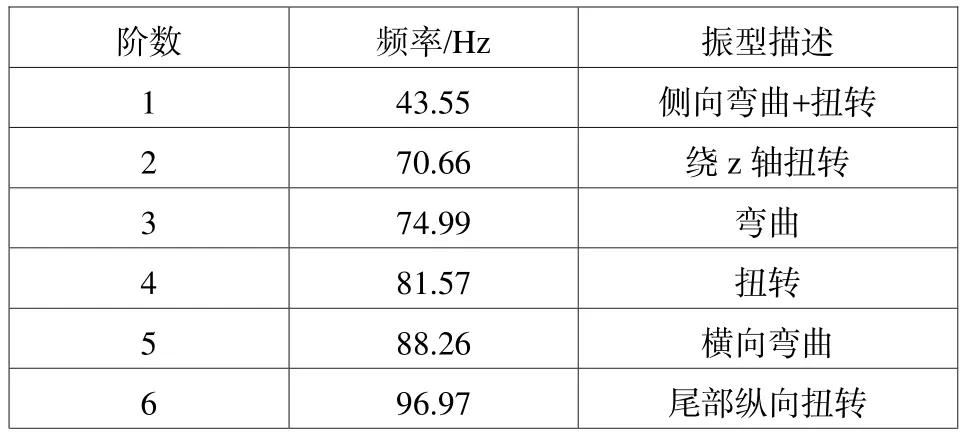
表2 车架固有频率和振型Lab.2 Frame inherent frequency and vibration mode

分析结果表明，车架最低阶振动频率为 43.55Hz，有效避开了路面和车轮不平衡引起的激励频率。车架第六阶固有频率为 96.97Hz，尽管接近发动机的怠速频率，但基本上避开了此值，可避免扭转共振发生。因此，本车架结构有效地避开了能引起共振的频率范围，设计满足振动要求。

4、结束语

通过对车架有限元模型进行自由模态分析，得到了车架结构的固有频率和固有振型，这不仅可以反映结构的动刚度特性，而且还是分析结构动力响应和其他动力特性问题的基础[5]。分析结果表明，所设计的车架结构基本满足振动要求，但发动机工作条件存在不确定性，所以想要更好地避开发动机怠速频率，避免引起结构疲劳损坏，可以在发动机舱区进行结构加强。

[1] 中国大学生方程式汽车大赛规则委员会.中国大学生方程式汽车大赛规则[Z].2013.

Rules committee of Formula Student China.Rules of Formula Student China[Z].2013.

[2] 周永光,阳林,吴发亮,邓仲卿.FSAE赛车车架结构优化和轻量化[J].广州：广东工业大学学报，2012.

Zhou Yongguang,Yang Lin,Wu Faliang,Deng Zhongqing.The structure optimization and lightweight of FSAE car frame[J].Guang zhou:Journal of Guangdong university of technology,2012.

[3] 汪伟.车架结构有限元分析与优化设计.南昌大学硕士学位论文，2009.

Wang Wei.Finite element analysis and optimization design on vehicle frame structure.Master dissertation of Nanchang university, 2009.

[4] 王家豪,张浩锴 FSAE管阵式车体骨架机构设计与分析[R].广州:华南理工大学,2010.

Wang Jiahao, Zhang Haokai.FSAE tubular body frame structure design and analysis[R].Guang zhou:South China University of Technology,2010.

[5] 张胜兰，严飞.基于 HyperWorks的车架模态分析[J].沈阳：机械设计与制造，2005.

Zhang Shenglan,Yan Fei.The analysis for the modals of frame based on hyperWorks[J].Sheng yang:Machinery Design and Manufacture, 2005.

The Finite Element Modeling and Modal Analysis of Formula Frame

Zhang Baoyu, Li Ping

(Automobile & Transportation Engineering College, Liaoning University of Technology, Jiangsu Huai’an 121001)

Modal analysis of Students formula car frame is of great significance for reducing the vehicle vibration and improving the dynamic performance. Established geometrical model of formula car frame in the CATIA software, then import it into finite element software HyperMesh and mesh, load and constraint it , and free modal analysis was carried out on the frame. Through Optistruct calculation, got the frame each order natural frequency and vibration mode, so that analyzed the possibility of resonance of frame structure.

racing car frame; finite element; modal analysis; sympathetic vibration

U463.8

B

1671-7988(2015)05-70-03

张宝玉，讲师，江苏食品药品职业技术学院，硕士研究生。