三相感应电机SVM-DTC系统

刘健楠，马西庚，孔鹏，李香香

（中国石油大学（华东）信息与控制工程学院，山东东营257061）

1 引言

直接转矩控制技术能够取得很高的转矩控制性能，在交流传动系统中得到了广泛的应用。其独特的零速满转矩输出特性以及对速度传感器依赖性低的特点使其成为挖掘机、网电修井机等大型机电设备的首选技术方案。

传统的直接转矩控制系统包含两个滞环比较器，将电机转矩、定子磁链的给定值与实际值之差限定在滞环范围内，逆变器只有在差值达到滞环比较器容差上下限时开关状态才会改变，这显然造成了逆变开关频率的不固定，会产生大量电磁干扰，同时影响散热［1］。另外，传统直接转矩控制系统还采用开关选择表进行最优电压矢量的选择，而这正是其控制电机输出转矩脉动过大的主要原因。有学者将传统磁链轨迹的6扇区细分为12个扇区，通过工作矢量在转矩调节作用效果上的差异对转矩调节信号进一步划分，增加了控制余地［2］。这种方法可以适当降低转矩脉动，但其本质仍是基于开关选择表的控制，优化能力有限。在此基础之上，还有学者提出使用模糊控制技术的策略。此方案可以进一步优化转矩脉动，但仍是以开关选择表为基础，另外，模糊控制器结构复杂，为实际应用增加了难度［3］。

针对上述问题，本文引入了一种基于空间矢量调制的三相感应电机直接转矩控制系统。该系统摒弃了传统的滞环控制器与开关选择表，代之以2 个PI 调节器及1 个SVPWM 发生器，控制过程中无需查表，可由基本电压矢量合成任意所需矢量，有效地对转矩与定子磁链同时调节。所需矢量的合成采用5 段式合成方式，在确保了直接转矩控制优秀性能的前提下，可以有效减小转矩与磁链的脉动。同时在每个载波周期内，系统能够保证逆变单元开关管各通断1 次，使得开关频率近似保持恒定，增强了系统的鲁棒性。

2 SVM-DTC系统方案

实现SVM-DTC 方案的结构主要包括磁链闭环控制结构、磁链转矩无差拍控制结构以及转矩闭环控制结构。磁链闭环控制结构方案要用到定子磁链与转子磁链观测器，因此，要掌握所有的电机参数，这会使得系统过分依赖电机参数，抹煞了直接转矩控制技术的优点，同时控制结构中缺少转矩闭环，降低了系统的鲁棒性。磁链转矩的无差拍控制方案要求非常精确的数学模型，稍有偏差就会导致输出电压的震荡，影响系统的稳定性。目前常用的方案为转矩闭环控制方案，其结构如图1所示［4］。

图1 SVM-DTC转矩闭环控制控制方案Fig.1 SVM-DTC scheme with closed-loop torque control

这种方案采用转矩闭环得到转矩误差值，经过1 个PI 调节器配合定子磁链角度与给定定子磁链可以得到1 个预测磁链，然后通过与实际磁链的比较得到1个参考电压矢量实现转矩与磁链的补偿。在SVM 模块中，通过基本的电压矢量能够合成任意矢量，以所需矢量在静止坐标系下的两分量作为输入信号从而能够实现其合成。这种方案比较简单，但是利用转矩参与到了磁链的补偿过程，这样使得磁链的调节受到转矩影响。因此，本文采用了一种定子磁链定向控制方案，通过磁链、转矩的实际值与给定值之差直接得到参考电压矢量，从而能够实现电压与转矩的精确补偿，其结构如图2所示［5-6］。

图2 SVM-DTC定子磁链定向控制方案Fig.2 SVM-DTC scheme with stator flux oriented voltage control

2.1 参考电压矢量

本文提出的SVM-DTC 采用的是基于静止坐标系下定子磁链定向的控制方案，如图2所示，控制系统中采用了转矩与磁链2 个闭环，其输出分别经过PI调节器可得到定子电压分量ud，uq，其中ud只影响定子磁链的幅值，而uq只对转矩的调整起作用，二者实为1个电压矢量的2个分量，而该矢量能够同时补偿电机电磁转矩和定子磁链误差，此电压矢量即为参考电压矢量。

此时的矢量是基于dq旋转坐标系下的矢量，但由于基本矢量的分析都是在静止坐标系下进行的，我们有必要将其变换到αβ静止坐标系下。dq-αβ的变换公式如下：

式中：θ为定子磁链轨迹的角度。

根据参考电压矢量在静止坐标系下的分量即可求得矢量相位角，从而判断其所在扇区。相位角计算公式如下：

2.2 空间矢量调制原理

直接转矩控制系统以两电平逆变器可输出的6个工作电压矢量为据对参考电压的工作区间进行了扇区划分，其划分情况如图3 所示。通过这样的扇区划分，无论所需矢量落在哪一区域，都可以由相邻两矢量配合零矢量合成，这是空间矢量调制的基本思想。

以扇区S1为例，如果参考电压矢量Vref落在S1扇区内，那么就可以利用v1，v2配合零电压矢量对其进行合成，见图4。

设定在一个采样周期Ts内，v1作用时间为T1，v2作用时间为T2，零矢量的作用时间为T0，那么首先T1，T2，T0与Ts应满足下式关系：

图3 逆变器工作电压及扇区划分Fig.3 Inverter operating voltage and sector distribution

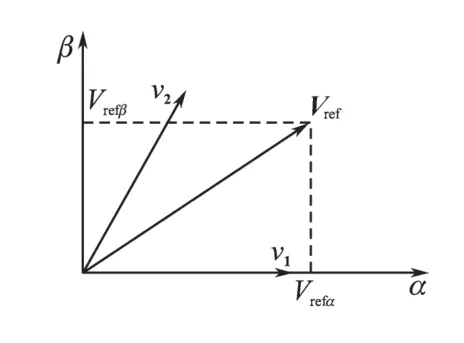
图4 扇区S1内静止坐标系下的参考矢量Fig.4 Reference voltage under α-β coordinateinsector1

其次，根据电压作用的伏秒平衡原理，通过下式关系即可得到v1与v2的作用时间：

其中，v1，v2的幅值应为直流母线电压值的2/3。其他扇区各矢量作用时间可通过类似的方法求得。值得注意的是，当所需合成的参考电压矢量的幅值超过基本工作矢量的幅值时，以此方式求得的T1和T2时间之和可能会超过1个采样周期，这时，需要对求得的电压作用时间进行修正，修正公式如下：

2.3 参考矢量的5段式合成

作为一种调制形式，空间矢量调制的最终输出也应该是一系列的脉宽调制波，波形与工作电压矢量的作用顺序紧密相关。为了保证在每一个载波周期内，逆变器开关管能够实现各通断1次，需要采用零矢量分散合成方案对参考电压矢量进行合成。一般按照对称原则，工作矢量分成3 段作用，配合开关变化最小原则在工作矢量中插入合适的零矢量，电压矢量作用顺序如图5 所示。其中，在工作矢量与参考矢量的各交点对称地插入零矢量，这种方案使得参考矢量的合成过程以零矢量开始，也以零矢量结束［7］。

图5 参考矢量的3段式合成Fig.5 3-section synthesis of reference voltage

如果在传统3段式合成方案的基础上进行修改，即将电压合成的过程进一步细化，可以得到一种5 段式的合成方案，其合成方式如图6a 所示。5段式方案所合成的矢量更加逼近于所需矢量，其工作矢量在合成轨迹上与参考矢量的分离幅值较3 段式方案更小，从而使得转矩与磁链的脉动更加减小。按照零矢量分散原则以及开关最小原则，图6b画出了各基本电压矢量在5段式合成方案中的作用时间顺序，以1 和0 分别代表开关管的通断。如图6所示该合成方式在每个载波周期仍然以零矢量开始和结束，1 个采样周期（2个载波周期）内，逆变单元开关管各通断2次，保证了开关频率的近似恒定。

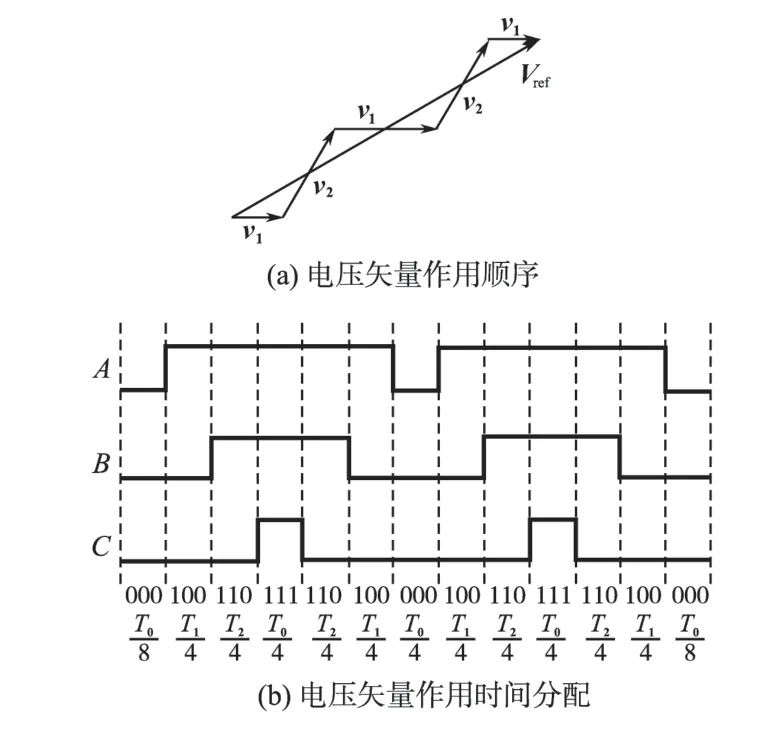
图6 参考矢量的5段式合成Fig.6 5-section synthesis of reference voltage

2.4 电机转速辨识

本系统中采用的感应电机转速辨识办法为模型参考自适应法（MRAS）。电机的转速可通过2个能够确定转子磁链在静止坐标系下分量的模型来获得，这2 个模型分别为转子磁链的电压模型与电流模型，其中电压模型方程为

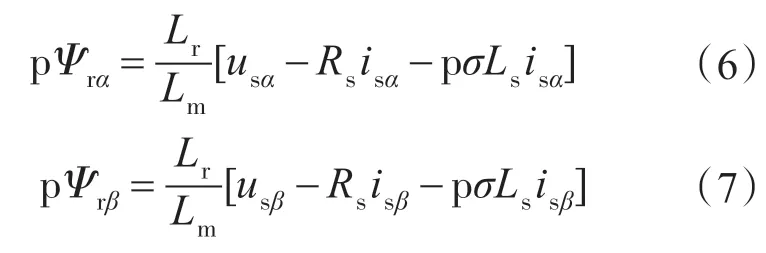
电流模型方程为

式中：Ls，Lr，Lm分别为电机定子绕组自感、转子绕组自感及定转子绕组间互感；Rs，Rr分别为定子电阻与转子电阻；Tr为转子电磁时间常数；σ为漏磁系数；p为微分算子为辨识转速。

转速辨识方案结构如图7所示［8］。

图7 转速辨识方案Fig.7 Speed estimation scheme configuration

由于电流模型中有转速参与了转子磁链的计算，所以将其选为自适应模型，相应的电压模型即选为参考模型。将2个模型的输出进行比较可得到一调谐信号，该信号经PI调节即可得到辨识转速。通过不断调整使调谐信号接近于0，此时的辨识转速与实际转速也就近似相等。调谐信号生成机制如下：

采用此调谐信号配合PI 控制器可以得到一非线性闭环系统，响应快速且稳定，同时系统算法中不涉及转子电阻，转子电阻的变化对转速辨识不产生影响。

3 仿真结果分析

本文通过使用Matlab/Simulink 组件对系统进行了建模仿真，其中感应电机选用额定功率为37 kW 的较大功率电机，初始给定转速800 r/min，初始给定转矩100 N·m。0.5 s 时，电机给定转速下降至0 r/min；0.75 s 时，给定转速升至500 r/min；1 s 时，改变给定转矩为300 N·m。仿真全程给定磁链幅值为1 Wb，时长1.2 s。系统的转矩响应、转速响应以及定子磁链轨迹分别如图8～图10所示。

本文同时对传统直接转矩控制系统、基于12扇区划分的直接转矩控制系统进行了仿真，并分别取相同时段的电机转矩、电机单相电流以及磁链幅值进行对比。

图8 SVM-DTC系统的转矩响应Fig.8 Torque response of SVM-DTC system

图9 SVM-DTC系统的转速响应Fig.9 Speed response of SVM-DTC system

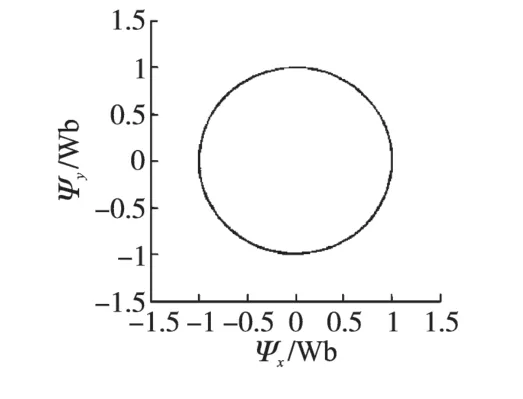
图10 SVM-DTC系统的定子磁链轨迹Fig.10 Stator flux trajectory of SVM-DTC system

图11为3 种控制方案下0.35～0.45 s 期间的电机电磁转矩，此时给定转矩为100 N·m。由于12扇区控制方案对转矩的控制选择余地更宽，所以其转矩脉动也明显小于传动控制方案，而SVM-DTC 采用了5 段式合成技术，其转矩脉动相比前两者有了显著改善。

图11 3种控制方案下的电机电磁转矩Fig.11 Motor electromagnetic torque of 3 control systems

图12 为3 种控制方案在0.4～0.5 s 期间的电机定子磁链幅值，此时给定转矩为100 N·m，给定转速为800 r/min。定子磁链幅值的波动直接影响了电机转矩响应波形的脉动，其3 种控制方案的波动比较结果也与图11 的转矩脉动比较结果一致。由于SVM-DTC 系统合成的电压矢量直接针对磁链与转矩的所需变化量进行补偿，该控制方案下的转矩与磁链脉动要比仅采用6个工作电压矢量进行补偿的控制方案大为优化。

图12 3种控制方案下的电机定子磁链幅值Fig.12 Stator flux amplitude of 3 control systems

图13为3 种控制方案下0.85～0.95 s 期间的电机C相定子电流，此时给定转矩为100 N·m，给定转速为500 r/min。尽管基于12 扇区的控制方案在电机转矩与定子磁链方面都较基本控制方案有所改善，但是通过图13可以发现其相应开关频率也更高，这体现了逆变开关频率不固定的缺陷。相比较而言，由于SVM-DTC 系统开关频率固定，其电流谐波含量也较基于开关矢量表的前两者控制方案大大减小。

4 结论

针对三相感应直接转矩控制系统存在的电机转矩脉动过大及逆变开关频率不固定的缺点，本文给出了一种基于空间矢量调制的直接转矩控制系统，并对其工作原理进行了阐述分析。通过对该系统进行建模仿真，结果表明该系统能够实现转矩与转速的快速响应，并实现零速满转矩输出特性。另外，与传统直接转矩控制系统及基于12扇区的改进直接转矩控制系统相比，此系统可以有效降低电机转矩与定子磁链脉动，且逆变开关频率固定，能够大大减小电机定子电流谐波，是更为优秀的控制方案。但是这种方案下的逆变开关周期为采样周期的二分之一，逆变器频率过高，该问题需要通过选择合适的采样频率来解决。

［1］韩如成，潘峰，智泽英.直接转矩控制系统理论及应用［M］.北京：电子工业出版社，2012．

［2］Üser Y，Gülmez K，Özen S．Sensorless Twelve Sector Implementation of DTC Controlled IM for Torque Ripple Reduction［C］//6thInternational Advanced Technologies Symposium，2011：317-321．

［3］王志强，刘建章，肖烨然.一种12电角度区间划分的异步电动机模糊直接转矩控制方法［J］.电气应用，2012，31（4）：30-35.

［4］黄志武，单勇腾，刘心昊，等.感应电机直接转矩控制三种方案的比较［J］.计算机仿真，2007，24（3）：326-332.

［5］Ouarda，Ben Salem.Induction Machine DTC-SVM：A Comparison Between Two Approaches［C］//10thInternational Multi-conference on Systems，Signals&Devices，2013：18-21．

［6］张瑞，高赟.异步电机空间矢量直接转矩控制的仿真研究［J］.大电机技术，2013（2）：23-26.

［7］阮毅，陈伯时.电力拖动自动控制系统［M］.北京：机械工业出版社，2009．

［8］Peter Vas. Sensorless Vector and Direct Torque Control［M］．New York：Oxford University Press，1998.