基于RLS的永磁同步电机离线参数辨识研究

王莉娜，薛飞

（北京航空航天大学自动化科学与电气工程学院，北京100191）

1 引言

永磁同步电机（PMSM）因具有高功率密度、大转矩惯量比和宽调速范围等优点，在工业机器人、数控机床和作动系统等运动控制领域得到了广泛应用［1］。随着永磁同步电机驱动系统在各行业领域中日益广泛的应用，对其控制性能提出了更高的要求。不论是采用矢量控制，还是直接转矩控制，其控制效果都依赖于电机模型参数的准确性，需要对电机参数进行辨识。通过离线辨识可以获得较准确的电机参数，从而实现：1）速度环、电流环调节器参数自整定，提高系统的动静态性能；2）转子速度估算，实现无速度传感器控制［2］；3）弱磁控制，拓宽调速范围。

电机参数的离线辨识主要通过直流试验、空载试验和堵转试验等试验方法对电机参数进行辨识，即在电机投入运行前，向电机施加不同形式的电压、电流激励信号，检测电机的电压、电流响应，按照它们的关系计算出电机参数或者采用某种拟合算法辨识电机参数。离线辨识一般具有激励信号易获取，算法简单的优点。

最小二乘辨识方法形式简单，在一定条件下具有良好的一致性和无偏性，既可用于在线辨识也可用于离线辨识，适用范围较广。递推最小二乘法不需要大矩阵求逆运算，计算量小，计算速度快，是一种比较理想实用的参数辨识方法。

文献［3］通过向电机注入高频信号，利用递推最小二乘法由dq 轴电压、电流离线辨识电阻电感，通过滤波减少干扰误差，但滤波器设计的好坏决定了最终辨识的准确性。文献［4］采用脉冲响应法辨识交直轴电感，并通过合理步骤减少死区对辨识的影响，但是在理论推导中做了近似处理。文献［5］通过空载试运行辨识电感，需要预先调试系统调节器的PI 参数。文献［6］采用交直流注入法辨识电感参数，辨识方法简单，辨识结果比较准确，但是没有对注入电压大小进行限定。

本文以面贴式永磁同步电机矢量控制系统为基础，采用直流注入方式对定子电阻和电感进行辨识。分析、补偿逆变器开关死区、管压降造成的电压损失，减小辨识误差。在辨识过程中结合递推最小二乘算法，减小采样噪声的影响。最后，通过仿真和实验对该方法的可行性和有效性进行了验证。

2 系统控制结构组成

系统整体控制框图如图1 所示，采用基于转子磁场定向的矢量控制策略，id=0 的电流控制方式；采用空间电压矢量脉宽调制方法（SVPWM）计算逆变器占空比；辨识部分位于虚线框中，独立于正常工作部分，给出激励信号，并依据电压、电流采样值，利用递推最小二乘法辨识电机参数。

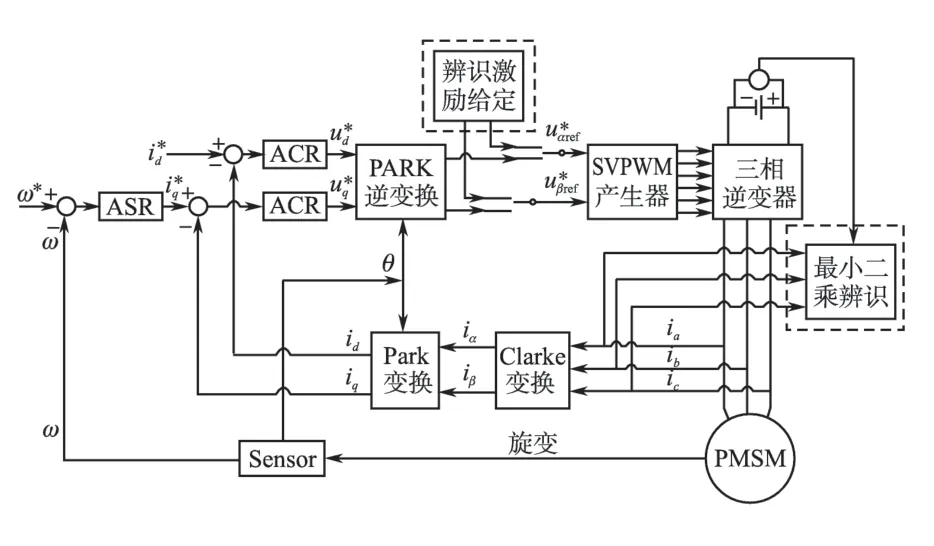
图1 系统控制框图Fig.1 The system control block diagram

3 电机参数离线辨识

3.1 定子电阻辨识

定子电阻的辨识通过施加直流电压，利用伏安法辨识。由于驱动器无法提供恒定直流电压，实际通过给定恒定占空比，经逆变器输出电压脉冲，在电机端获得等效直流电压。令=0，给定（其值的确定见第4 节），经SVPWM 调制方法，即可得到一个α轴方向的电压，大小等于初始，转子处于任意位置，通电后，转子d轴向α轴吸合，待稳定后，转子不再旋转，等效电路如图2所示。

图2 等效电路图Fig.2 Equivalent circuit

由定子U 相电流Iu和等效直流电压Ueq，可得定子电阻：

因逆变器输出端为脉冲电压，等效直流电压需通过给定激励电压计算得到。根据SVPWM和坐标变换，给定电压与理论等效直流电压存在如下关系：

在不考虑电压误差的情况下，可以认为Ueq与相等。利用给定电压和相电流Iu即可计算出定子电阻。

3.2 驱动器非线性因素对电阻辨识的影响

因为定子电阻辨识时，是以系统给定电压换算实际输出电压来处理，然而由于逆变器的开关死区以及IGBT和续流二极管的导通压降等非线性因素的存在，造成给定电压与实际输出电压之间存在误差。而电机电阻一般较小，辨识时给定的激励电压也较小，因此该差值对于电阻辨识的影响不可忽视。对电压误差的合理补偿关系到辨识结果的准确性。

图3 1个开关周期内的三相驱动脉冲Fig.3 Three-phase drive pulses within one switching cycle

以3.1 节辨识方法分析IGBT 和续流二极管的导通压降（包括死区时间内的部分）。如图3所示，在1个开关周期内，当逆变器输出非零电压矢量时（T2，T4期间），电流等效流过2 个IGBT；输出零电压矢量时（T1，T3，T5期间），即使上3 管或下3管均有导通信号，电流也只等效经过1个IGBT和1个续流二极管。则，由于IGBT和续流二极管导通压降造成的电压损失可表示为

式中：Vf为电压损失；Vsat为IGBT 导通压降；Vd为续流二极管导通压降；D为有效电压矢量占空比，表示逆变器输出非零电压矢量的时间占整个开关周期的比例。

对于给定较小的激励电压来说，D很小，则可以近似的将式（3）简化为

因此，考虑导通压降后的实际等效直流电压为

逆变器开关死区会造成输出电压波形发生畸变，产生电压误差［7］。死区引起的误差电压矢量大小为

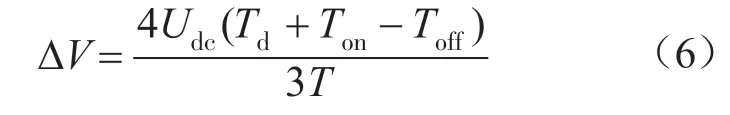
式中：Udc为直流母线电压；Td为设定死区时间；Ton为IGBT导通时间；Toff为关断时间；T为逆变器开关周期。

误差电压矢量的方向由三相电流极性决定。在本文中，给定电压矢量的方向固定，电机不转，因此三相电流的极性是固定的，故误差电压矢量方向也是固定的，与给定电压矢量方向相反。实际给定电压的大小为

将式（2）、式（5）、式（7）带入式（1），可得电阻的计算公式为

3.3 电感辨识

在转子保持静止不动，即ωr=0的条件下，永磁同步电机在同步旋转坐标系下的d轴电压状态方程为

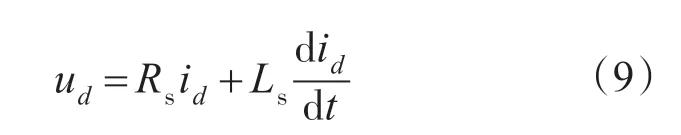
当给定ud阶跃信号，电流将按指数规律增加；当撤去ud阶跃信号，电流按指数规律衰减。根据一阶RL 电路的全响应计算方法，可知电流响应满足

根据上式，在定子电阻已知的条件下，观测电流随时间的变化，即可辨识电感。根据3.1 节辨识电阻后的条件，转子d轴与α 轴重合，此时，

在α轴施加阶跃电压信号，就能够形成辨识电感的条件，以相电流iu替换id，即可利用式（10）计算电感。

3.4 非线性因素对电感辨识的影响

电感辨识只涉及到初始电流和最终响应电流，不受死区电压误差的影响，在电流不过零的情况下，零电流钳位也不会影响电流响应过程。因而死区造成的非线性因素对电感辨识的影响在电流不过零情况下可以忽略。但要保证在整个电流增加、衰减过程中给定电压都要超过死区影响范围。

若ud阶跃电压初值或终值过零，则IGBT 和续流二极管的导通压降会使式（9）形式变为

构成一阶非齐次微分方程，求解复杂。为消除导通压降的影响，令激励电压始终存在一个基值电压Ubase（其值的确定见第4 节），在此电压基础上进行阶跃给定。则可以消除上述非线性因素的影响，仍可按式（10）计算。基值电压的存在，也可以保证转子d 轴始终与α 轴吸合不运动，防止撤除电压时出现电机转动的情况，使其能很好地满足ωr=0的条件。

3.5 递推最小二乘算法

在上述方法的基础上，结合最小二乘法，有助于减小电流、电压采样干扰因素，提高辨识精度，同时可以减小数据存储量，提高运算速度。最小二乘的基本形式为

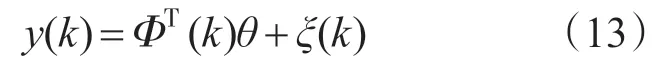
式中：y(k)，ΦT(k)为系统可观测的输入输出量；θ为待辨识量；ξ(k)为系统残差。

将系统满足的等式变形为最小二乘的基本形式，即可采用最小二乘方法辨识参数。为了减少辨识过程中的大矩阵求逆及大量运算，采用递推最小二乘算法。其算法具体实现如下［8］：

式中：Kk+1为增益矩阵；Pk+1为协方差阵，其初始值为P0=10αⅠ，α一般取较大的正整数（如取3～5）；Ⅰ为单位阵；估计参数初值般可取很小的值（如0.000 1）。

对于电阻辨识，将式（8）变形为

满足最小二乘基本形式，由激励电压和电流采样值即可辨识定子电阻。

电感辨识时，将式（10）取对数后变形可得：

已知初始I0和最终电流I∞，采样电流值并记录时间，即可辨识电感。

由于两式均为一阶标量方程，递推最小二乘算法中的矩阵转置可简化，简小了计算量。

4 辨识步骤

具体辨识步骤如图4 所示。为减小采样误差，提高辨识精度，应尽可能获得大的响应电流。故在辨识初始t0—t1时段缓慢增加激励电压，使电流达到某一合理值，本文选取略小于额定电流值，通过此过程既可获得激励电压的最大给定值，同时也能使任意初始态的电机转子d 轴与α轴吸合。t1—t2时段保证电流最终达到稳定。t2—t3辨识电阻，并得到电流最大时的稳定值I1。然后逐渐减小激励电压使电流降为额定值的50%左右，得到基值电压Ubase及此条件下的电流I2。t4时刻给定阶跃电压，以t2—t3时刻辨识得到的电阻值，采集的电流值I1，I2作为已知条件辨识电感，t5—t6时刻继续辨识电阻。t6—t7以更新的电阻辨识值和新采集的电流最大值I1替换原已知量，利用电流衰减过程继续辨识电感。并在基值电压给定下再采集电流值I2。一般电阻与电感的比值较大，阶跃时直流递增衰减过程较快，可辨识的时间较短，所以进行多次电感辨识，增加数据量，以保证电感辨识的准确。

图4 辨识步骤图Fig.4 Steps diagram of the identification

5 仿真结果

仿真所用电机参数为：定子绕组电阻R＝0.331 Ω，定子直轴电感Ld＝2.1 mH，极对数pn＝4，转子转动惯量J＝0.025 2 kg·m2，额定转矩T＝75 N·m，额定电压UN＝380 V，永磁体磁链Ψ＝0.353 7 Wb，定子交轴电感Lq＝2.1 mH，摩擦系数B＝0.001 1 N·m·s，额定转速n＝1 700 r/min，额定电流I＝23 A，额定功率PN＝13.5 kW。

在Simulink 仿真环境下，建立离线参数辨识仿真模型，如图5 所示。该模型中略去了正常工作情况下的PI调节器和坐标变换部分。

图5 简化离线辨识Simulink仿真模型Fig.5 Simulink model of the simplified offline identification

仿真中，IGBT导通压降设为1.7 V，续流二极管导通压降为2.3 V。逆变器开关频率5 kHz，死区时间为3 μs。参数辨识计算步长为100 μs。仿真中简化了最大激励电压获得过程，没有加入激励电压递增递减过程，采取直接给出一个合适电压的方式。得到仿真电流波形和电阻电感辨识曲线如图6所示。

在激励信号注入初期，由于电机转子d 轴未与α轴重合，存在一个转动过程，电流有一定的波动变化。待转子吸合稳定后电流趋于稳定。

图6 辨识仿真波形Fig.6 Simulation waves of identification

在t=0.2 s处辨识电阻，可以看出电阻辨识值快速趋于稳定值，电阻误差很小。在t=0.4 s时利用阶跃电压辨识电感，电感辨识值也很快稳定，辨识过程较快。之后的过程在之前数据的基础上继续辨识电阻、电感，增加辨识数据量。

通过以上的仿真说明，利用最小二乘法采用直流伏安法和直流衰减法辨识电机电阻、电感的方法理论上是可行的。对驱动器死区及IGBT续流二极管对电压误差的分析及近似补偿也是合理的。

6 实验研究

本文采用TI 数字信号处理器（DSP）TMS320F28335 和三菱智能功率模块PM100RL1A120 搭建驱动器硬件平台。其中电机参数见第5 节。电压、电流信号的采样频率均为10 kHz。通过示波器观测电机电流，由CCS软件提取DSP数据绘制辨识结果。

考虑到DSP 中PWM 比较器的分辨率的影响，给定电压和实际逆变器输出电压仍有一定的误差，先通过采样的直流母线电压和PWM 比较器值反推给定电压值，再按照上文方法进行后续辨识计算。直流母线电压越高，有效电压占空比越小，造成死区影响也相对增大，因而需要适当增大激励电压，或者降低逆变器开关频率。

图7 U相电流波形Fig.7 Waves of U-phase current

U 相电流波形如图7 所示，电流波形初始为电压递增递减确定辨识电压最大值和基值的过程，之后为阶跃辨识电阻、电感过程。在阶跃过程中电流符合指数曲线规律。

辨识过程总时间为4.5 s，时间较短。由图8可看出，电阻的辨识结果很快趋于稳定，可以进一步缩短电阻辨识时间。最终得到的电阻辨识值为0.333 6 Ω。由于直流衰减过程很短，数据较少，电感辨识值有较小的波动，如图9所示。最终得到的辨识结果为2.104 mH。辨识结果与仪器测量结果接近，误差较小。

图8 电阻Rs辨识波形Fig.8 Waves of resistance identification

图9 电感LS辨识波形Fig.9 Waves of inductance identification

表1 所示的实验结果显示，电阻的辨识结果基本相同，较实际结果稍大，存在一定量的接线电阻的影响。由于电阻辨识结果的误差，也会对电感辨识结果产生一定的影响。采样频率会影响电感辨识结果的稳定，当将采样频率改为20 kHz时，电感辨识结果不再波动。

表1 5次辨识结果Tab.1 Five identification results

分析误差主要来自于：

1）IGBT、续流二极管导通压降受电流大小的影响，不能精确的补偿；

2）PWM驱动信号会受到光耦等中间传输器件以及IPM 自身导通关断时间因电流大小而变化的影响，死区时间会有一定的变化；

3）电压、电流采样存在误差，且受分辨率的限制；

4）采样频率较小造成数据较少，影响电感的辨识。

7 结论

本文主要研究面贴式永磁同步电机的电阻、电感参数离线辨识，考虑了逆变器开关死区等延时，IGBT、续流二极管导通压降等非线性因素造成的电压误差，提出了补偿方法，并通过注入基值电压的方法消除IGBT和续流二极管导通压降对电感辨识的影响。结合递推最小二乘法，进一步提高了辨识速度和准确性。该辨识方法简单，由于采用最小二乘法，对采样误差有一定的抑制作用。辨识速度快，准确度高，具有一定的实用性。

［1］李光泉，葛红娟，刘天翔，等.永磁同步电机调速系统的伪微分反馈控制［J］.电工技术学报，2010，25（8）：18-23．

［2］张虎，李正熙，童朝南.基于递推最小二乘算法的感应电动机参数离线辨识［J］. 中国电机工程学报，2011，31（18）：79-86.

［3］Omrane I，Etien E，Bachelier O，et al. A Simplified Least Squares Identification of Permanent Magnet Synchronous Motor Parameters at Standstill［C］//Industrial Electronics Society，IECON 2013-39th Annual Conference of the IEEE.IEEE，2013：2578-2583.

［4］吴家彪，马钧华. 伺服系统永磁同步电机参数辨识策略［J］.轻工机械，2013，31（6）：45-50.

［5］张斯瑶，刘桂花，王卫.变频空调压缩机电机的参数辨识方法［J］.电源学报，2013（1）：95-100.

［6］陈振锋，钟彦儒，李洁.嵌入式永磁同步电机离线参数辨识技术［J］.电力电子技术，2009，43（11）：43-44.

［7］吴茂刚，赵荣祥，汤新舟.正弦和空间矢量PWM 逆变器死区效应分析与补偿［J］.中国电机工程学报，2006，26（12）：101-105.

［8］杨承志，孙棣华，张长胜.系统辨识与自适应控制［M］.重庆大学出版社，2003.