高压MMC变换器低频运行特性分析及控制方法

高会民，谢小英，杜金桥

（国网冀北电力有限公司秦皇岛供电公司，河北秦皇岛066000）

1 引言

6 kV/10 kV高压电机在现代电力传动系统中应用广泛，与中、小电压等级电机相比，其具备运行效率高、启动电流低、无需降压变压器等诸多优势［1-2］。然而，受限制于现有功率开关器件（IGBT，IGCT等）的耐压等级，将中压等级（1 140 V，3 300 V）中应用最为广泛的二极管中点钳位式（neutral point camped，NPC）三电平拓扑推广至10 kV 高压场合时困难重重［3］。针对上述问题，西门子、ABB 等公司均给出了多电平拓扑的解决方案，其中西门子公司推出的模块化多电平（MMC）拓扑结构在保持传统多电平变换器优点的基础上，更是具备了模块化设计、故障容错运行、单一电源供电、恶劣电网适应性等优势，使得MMC拓扑成为6 kV/10 kV 高压电机驱动领域中极具前景的设计方案［4-5］。

为了保证MMC 系统的正常运行，需要对其子模块电容电压进行均压控制。MMC拓扑存在的低频电容电压波动现象是限制其运用于高压电机驱动的关键问题。为此，本文在建立MMC拓扑数学模型的基础上，分析了子模块电容电压波动规律，在此基础上提出了一种基于高频信号注入的MMC 多电平变换器低频调制方法。最后，搭建了1 台3.2 kW 的MMC 实验样机进行高频信号注入法的可行性与高效性验证。

2 MMC拓扑数学模型

如图1 所示为MMC拓扑结构，上、下桥臂各由N 个子模块（single module，SM）和1 个桥臂电抗L 串联组成，其中：SM 由2 个开关器件和1 个储能电容组成。各个SM 可处于投入、切除和闭锁3种工作状态。通过控制各子模块的投切可实现桥臂输出电压Varm在0～Vdc之间自由调节。

图1 MMC拓扑基本结构Fig.1 The basic structure of MMC topology

根据子模块的工作特性，可将单个桥臂所有子模块SM等效为1个可控电压源，忽略上、下桥臂电抗之间的互感，根据基尔霍夫电压定律可得：

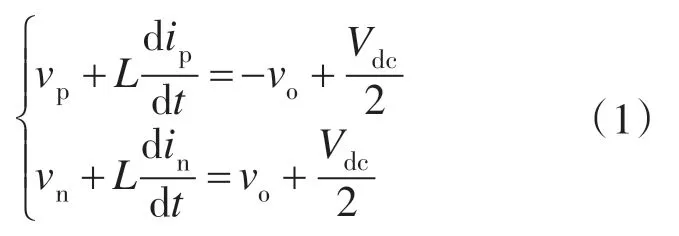
式中：vp为上桥臂子模块电容电压之和；vn为下桥臂子模块电容电压之和；ip为上桥臂电流；in为下桥臂电流；vo为单相输出电压；Vdc为直流母线电压。

根据基尔霍夫电流定律可得：

式中：io为输出相电流。

考虑到子模块电容电压的均衡控制策略，假设子模块电容电压均相等，为便于控制以及能量在各相之间均衡分布，子模块电容电压额定值一般设定为Vdc/n。因此，上、下桥臂子模块电容电压之和分别为

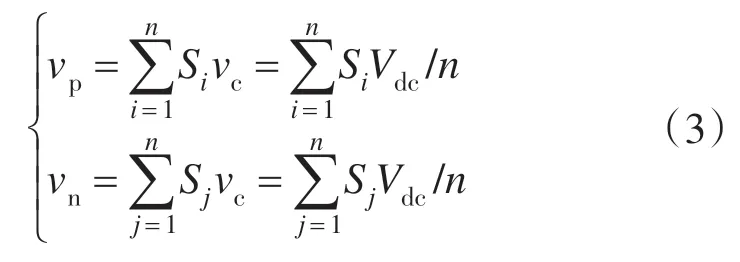
式中：Si，Sj分别为上下桥臂子模块数。

利用桥臂电抗可以对环流进行抑制的特性，在保证桥臂电抗压降平均值为零的前提下，同一相中上、下桥臂处于投入状态的子模块个数可以不严格互补。因此，可对经典的控制方法进行改进，使k1，k2满足下式的约束关系。

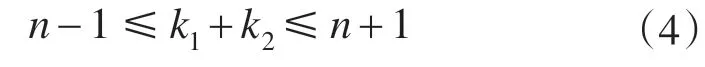
由式（4）可知，通过改变k1，k2的值，可在交流侧得到2n+1电平的相电压，每个电平的电压等级为Vdc/2n。这种方法每相中处于投入状态的子模块电容电压之和不恒等于直流母线电压，桥臂电抗将承受电压。当n=4 时，表1 给出了9 电平MMC 上、下桥臂子模块投入个数变化时所对应的交流侧相电压。

表1 MMC交流侧输出状态关系Tab.1 The AC output status of MMC

3 MMC子模块电容电压波动规律

为便于分析MMC 子模块电容电压波动规律，假设a 相输出相电压vao=Vmsin(ωt)，输出相电流ia=Imsin（ωt-φ）。其中，Vm为相电压峰值，大小等于mVdc/2；Im为相电流峰值；φ为相电压超前电流的相位角。则3项输出瞬时功率P为

假设三相子模块电容储存能量的总量始终保持不变，则输出功率全部由直流母线提供，根据能量守恒原则可得：

至此，a相上、下桥臂瞬时功率Ppa，Pna为

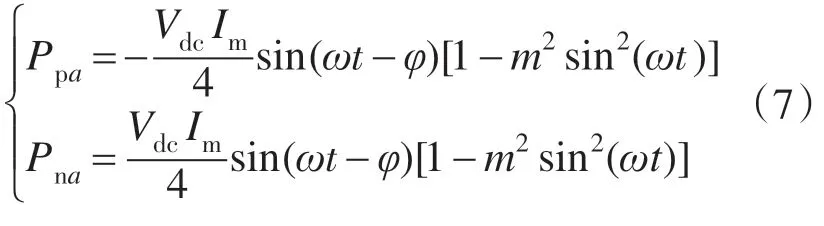
由式（7）可知，Ppa，Pna大小相等符号相反，且均为周期性函数，1 个周期内积分值为零。由此可知，同一相上、下桥臂输出瞬时功率互补，一相总能量保持不变；上、下桥臂子模块电容均进行周期性充放电，且在1 个周期内充放电能量达到平衡。

子模块电容所储存能量的变化可以反应子模块电容电压的波动，因此，在半个周期内通过对单个桥臂输出功率进行积分可得到子模块电容电压的波动情况。以上桥臂为例进行分析，因调制度m<1，则式（7）中1-m2sin2(ωt)≥0，则Ppa2个过零点θ1，θ2为

t1时刻对应θ1，t2时刻对应θ2，则Ppa在t1～t2区间内小于零，子模块电容一直从外界吸收功率，造成储存能量一直增加，增加量ΔWpa为

由式（9）可知，MMC 直流母线电压确定后，子模块电容所储存能量的波动与相电流峰值Im成正比，与输出角频率成反比，理论上频率为0 Hz运行时，电容电压波动将无穷大。因此，MMC不适用于低速大转矩启动或低速重载运行的高性能调速领域。然而，风机、泵类等负载转矩与转速平方成正比，低速运行时转矩较小，相应较小的负载电流可减小电容电压的波动，且该类负载调速范围较窄，一般运行在30～50 Hz，MMC应用于风机、泵类等调速领域时，主要解决0～30 Hz启动过程中电容电压波动问题即可。

4 高频信号注入方法

由子模块电容电压波动规律可知，桥臂功率的波动频率和幅值可影响电容电压的波动，若保持桥臂功率的波动幅值不变，通过提升桥臂功率的波动频率可降低电容电压的波动幅值。通过合理注入高频零序电压，桥臂电流和桥臂电压将会出现高频分量，桥臂功率的波动将会由低频转为高频，进而可减小低频运行时电容电压的波动幅值。

假设桥臂所叠加高频零序电压为vz，a相所叠加高频相间环流为ipza，此时a相桥臂电流、电压分别为

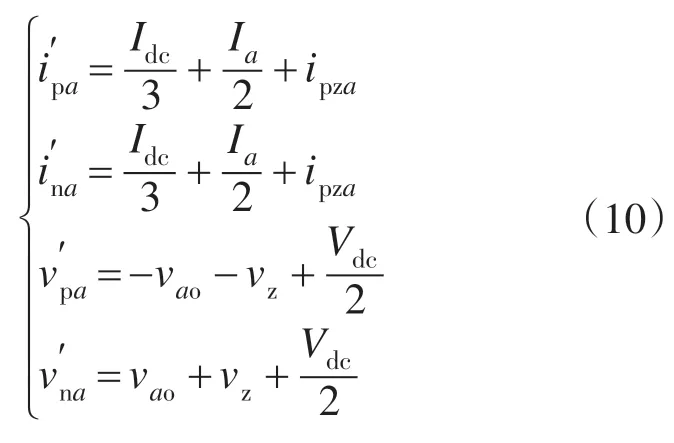
其中

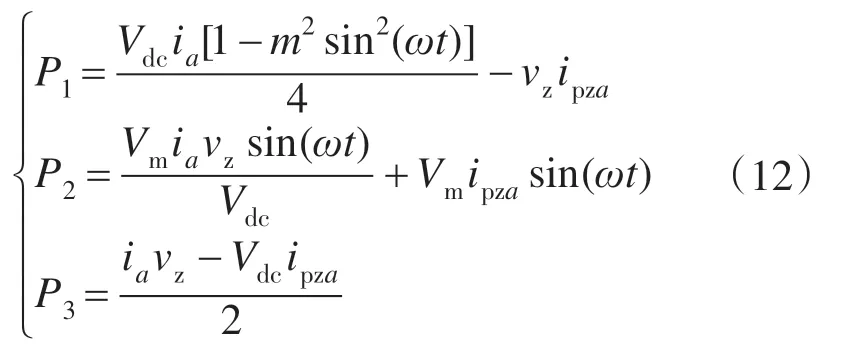
由式（12）可知，叠加高频分量vz，ipza后，P2，P3将只含高频成分，而P1仍含低频成分，若使桥臂功率只含高频成分，应消除P1中的低频成分或使其等于0。令P1=0，利用正弦函数积化和差的特性，可将P1中的高频成分vzipza通过积化和差运算产生与P1低频成分Vdcia[1-m2sin2(ωt)/4]大小相等符号相反的分量，进而抵消低频分量的影响。则相间环流ipza为

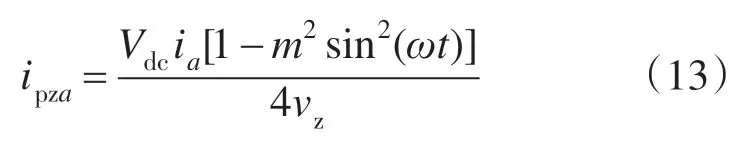
设高频零序电压vz表达式为

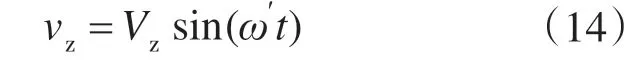
式中：Vz为零序电压峰值；ω′为零序电压角频率。

MMC 采用CPS-SPWM 进行调制时，相电压峰值与零序电压峰值应满足：

由式（15）可知，零序电压峰值Vz应取最大值为

5 MMC样机实验

MMC 实验样机主要技术参数为：额定功率3.2 kW，直流母线额定电压640 V，直流母线额定电流5 A，桥臂子模块个数4 个。为便于集中控制，各子模块均配备独立控制器，控制系统采用3级控制架构，主控制器和辅助控制器集成在主控制板上，子模块控制器与主控制板采用光纤进行通信，从而保证了通信质量，避免了电磁干扰。

图2 为MMC 拓扑带阻、感负载时的稳态实验波形。图2a、图2b 为MMC 拓扑子模块电容电压，其中子模块电容电压波动由传统方法的5.8 V 降低到2.6 V，验证了MMC 高频信号注入法的可行性；图2c、图2d 为MMC 拓扑上、下桥臂电流，高频信号注入后桥臂电流中除了含有基频分量（20 Hz）和2 倍频分量（40 Hz）外，还含有高频分量，与理论分析结果相符；图2e、图2f为MMC 拓扑输出相电压，传统方法中相电压为5 电平阶梯波，主要分量为基频分量（20 Hz），高频信号注入后相电压除含有基频分量（20 Hz）外，还含有高频分量，结果验证了高频信号注入法的可实现性。

图2 带阻、感负载时MMC稳态实验波形Fig.2 MMC steady state test waveforms with R L load

图3为MMC 拓扑带异步电机全速段运行实验波形，异步电机采用经典的V/f控制方法进行控制，稳定运行频率设为50 Hz，启动时间设为20 s。图3a、图3b为动态过程中上、下桥臂子模块电容电压实验波形，由图3a、图3b可知，高频注入法将低频段电压波动值由35 V 减小为5 V，电容电压在低频段波动的问题得以解决；图3c、图3d 为动态过程中输出线电压Vab实验波形，由图3c、图3d 可知，高频注入法Vab低频段波形满足V/f 控制要求，线电压幅值随频率的增大而线性增大，从而保证电机稳定运行；图3e、图3f 为动态过程中电机相电流ia实验波形，可以看出传统方法中出现的电流冲击、震荡等问题均得到了抑制，电机启动性能将得到明显改善，实验结果与理论分析结果相符。

图3 带电机负载时MMC动态实验波形Fig.3 MMC dynamic state test waveforms with motor load

6 结论

本文研究了一种高压多电平MMC变换器高频信号注入方法，通过相关理论分析和样机实验验证可以得出以下几点结论。

1）MMC 拓扑具备的模块化结构、故障容错运行、单一电源供电、恶劣电网适应性等优势，使其适用于6 kV/10 kV 高压风机、水泵等调速领域。

2）基于高频信号注入的MMC 拓扑控制方法，有效地克服了MMC 拓扑低频段子模块电容电压波动，避免了传统方法中出现的电流冲击、震荡问题，电机启动性能得到明显改善。

［1］李长利.高压变频调速在主抽风机同步电机上的应用［J］.电气传动，2012，42（10）：69-71.

［2］石志辉.300 MW 机组凝结水泵变频改造技术方案及节能分析［J］.电气传动，2011，41（8）：40-44.

［3］王昌南，何凤有，田明.大功率三电平防爆变频器散热分析及计算［J］.工矿自动化，2013（1）：88-91.

［4］Hagiwara M，Akagi H.Control and Experiment of Pulsewidthmodulated Modular Multilevel Converters［J］.Power Electronics，IEEE Transactions on，2009，24（7）：1737-1746.

［5］戴鹏，郭全军，梁改革，等.模块化多电平变流器调制策略研究［J］.电气传动，2014，44（1）：49-52.