低开关频率下三电平同步对称SVPWM算法实现

吴强，袁庆庆，王钊，伍小杰

（中国矿业大学江苏省煤矿电气与自动化工程实验室，江苏徐州221008）

1 引言

在大功率应用中，三电平逆变器中IGBT 或IGCT 的开关频率一般控制在500 Hz 以内［1］，低开关频率能有效降低开关损耗并增大装置输出功率，但会使波形畸变增大［2-4］。

将每个基波周期内的开关脉冲数P定义为开关频率fsw与基波频率fs之比，即P=fsw/fs。按脉冲个数和相位是否固定，可将调制方式分为异步和同步调制两大类。异步调制会产生除6k±1（k为整数）之外的非特征次谐波，在开关频率fsw很低时，非特征次谐波影响不可忽视，此时若采用同步对称调制，即保证输出电压波形三相间对称、每相电压1/2正负半周期奇对称（1/2周期对称）、半周期内1/4 周期偶对称（1/4 周期对称）［4］，有助于优化谐波性能。

传统调制方式仅当P为3的奇数倍时才满足同步对称要求［5］。由于脉冲数不能连续变化，当逆变器带负载进行变频调速时，存在开关频率随基波频率在较大幅度内变化的情况，影响分段同步调制效果。因此，对于在任意脉冲数下实现同步对称调制的研究具有实际意义。

文献［5］使用钳位电压和零状态转化的策略，实现了当脉冲数为奇数时的两电平同步对称调制。文献［6］根据调制度设计多种开关切换规则实现三电平同步对称调制，但未给出脉冲数为3的偶数倍时的规则。如果采用特定谐波消去法和电流谐波最小法，可使输出波形满足同步对称性［4］，但两者的开关角多为离线计算，且涉及超越方程，算法较为复杂。

本文首先分析了同步对称调制特征，推导得出三电平同步对称SVPWM 的两个基本条件，在此基础上按脉冲数讨论开关切换的对应规则，实现了任意脉冲数下的同步对称调制。通过仿真分析了谐波优化情况，使用DSP 实现算法，并在三电平NPC逆变平台上进行了具体实验。

2 同步对称SVPWM实现方法

2.1 简化三电平SVPWM算法

由于简化三电平SVPWM 在选择基本矢量和设计开关切换规则上，有两电平SVPWM 的直观性，在此算法上进行同步对称算法优化［7］。将三电平空间矢量图分成6个大扇区B1～B6，每个大扇区分为6 个小扇区S1～S6，如图1 所示。将三电平参考电压矢量Vr通过坐标平移，修正为以小矢量V1为等效零矢量的两电平参考电压矢量V′r。修正关系如图2所示，关系式为

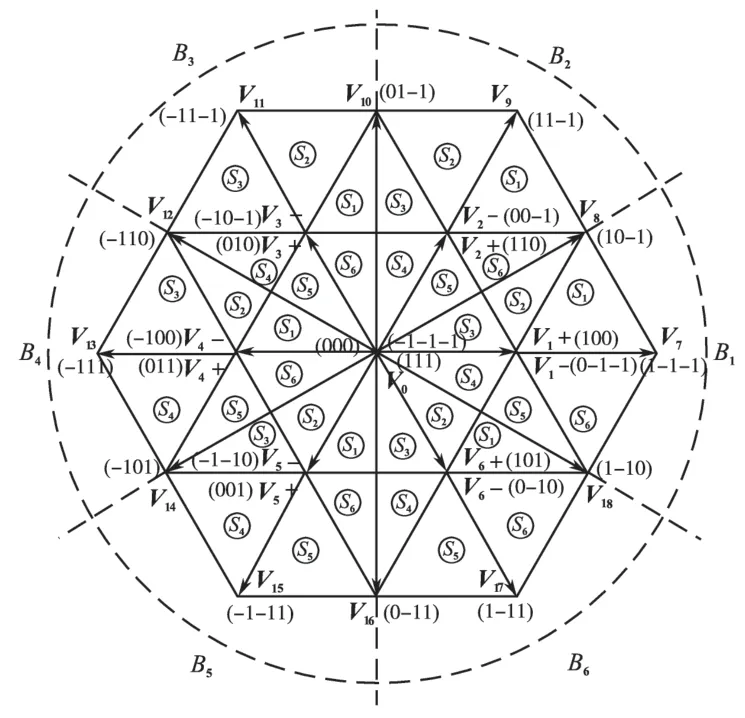
图1 简化三电平SVPWM空间矢量图Fig.1 Simplified three-level SVPWM space vectors

图2 矢量修正与采样位置Fig.2 Vectors correction and sample position

式中：Ts为采样周期；Udc为直流侧电压。

2.2 同步对称条件

通过分析同步对称输出波形的基本特征，推导矢量开关状态之间的关系，并进行归纳。

1）同步性。满足同步时基波周期内的脉冲个数和相位均固定，相电压幅值在θ与θ±2π处相等，对应的开关状态在θ与θ±2π处相同，为

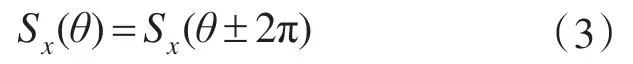
式中：Sx代表A，B 或C 相桥臂的开关状态；θ为与α坐标轴的夹角。

当每个周期的采样数P 为定值时，可以满足同步的要求。

2）三相对称。三相对称意味着三相输出电压互差120°。这需要A 相在θ处的开关状态与B 相在θ+2π/3处，C相在θ-2π/3处的开关状态相同，为

例如，θ处的开关状态为101，则θ+2π/3 处的开关状态为110，θ-2π/3 处的开关状态为011，同时对应矢量的作用时间要相等。

3）1/2 周期对称。基波电压正负1/2 周期关于过零点奇对称，即开关状态在θ与θ±π处相反，为

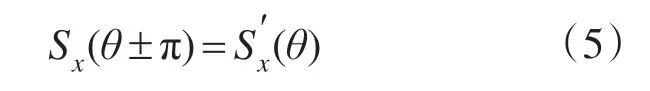
4）1/4 波对称性。波形关于峰值处1/4 周期偶对称，为

式中：θx为波形峰值处角度。

扇区内选取N（整数）个参考矢量，须使N 个矢量关于扇区对称轴对称，扇区对称轴两侧的脉冲个数和开关位置相同，即为偶对称，则θx在扇区的中心对称轴处。

对上述4 种关系进行归纳，得到同步对称调制必须同时满足的2 个条件：1）每个大扇区中采样数为整数；采样位置在扇区内平均分布，关于扇区中心轴线对称；2）相邻大扇区间对应采样处的开关状态满足下式

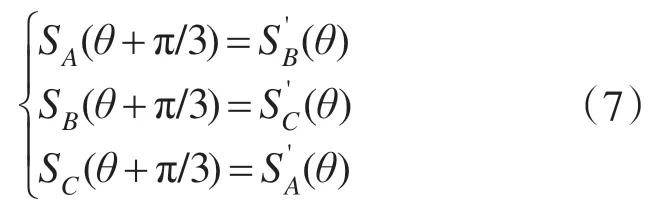
2.3 实现步骤

1）确定采样位置。按照条件1分配各采样位置，采样间距为π/3N；且各采样位置需关于扇区中心轴线对称。当采样数为奇数时，第1 个采样位置应在扇区边界处；当采样数为偶数时，第1个采样位置的角度θ=π/6N。N=4时采样位置如图2中虚线所示。

2）判断扇区。根据式（1）修正基本电压矢量，判断大小扇区号，确定合成矢量Vx，Vy，Vz。

3）时间计算。根据式（2）计算基本矢量的作用时间T0，T1，T2。

4）开关状态切换规则设计。由条件2 可知，只需设计一个扇区中的开关策略，再由式（7）推算到其他各扇区中，不同脉冲数下的策略不同，分为3种情况讨论。

①当N 为奇数，脉冲数P=（3N-1）/2 时。前N-1 个采样在扇区内，按照Vx+↔Vy↔Vz↔Vx-切换。第N 个采样处，矢量开关切换规则为Vx+→Vy→Vy→Vz，扇区最后一个矢量是Vz，此时它与下1 个扇区的第1 个矢量相同，切换时没有开关动作。以N=3，P=4 举例，具体规则：扇区B1，N=1，V1+→V18→V7→V1-；扇区B1，N=2，V1-→V7→V8→V1+；扇区B1，N=3，V1+→V8→V8→V2-；扇区B2，N=1，V2-→V8→V9→V2+。

②当N 为奇数，脉冲数P=（3N+1）/2 时。前N-1 个采样在扇区内，按照Vx-↔Vz↔Vy↔Vx+切换。第N 个采样处，矢量开关切换规则为Vz→Vy→Vy→Vx+，扇区最后一个矢量是Vx+，此时它与下一个扇区的第1 个矢量不相同，扇区切换时存在额外的开关动作。以N=3，P=5 举例，具体规则：扇区B1，N=1，V1-→V7→V18↔V1+；扇区B1，N=2，V1+→V8→V7→V1-；扇区B1，N=3，V2-→V8→V8→V1+；扇区B2，N=1，V2+→V9→V8→V2-。

③当N为偶数时，脉冲数P=3N/2时。第1个和第N 个采样的开关规则为Vx+↔Vy↔Vz↔Vy。其他采样位置开关规则均为Vx+↔Vy↔Vz↔Vx-，扇区切换时不存在开关动作。以N=4，P=6举例，具体规则：扇区B1，N=1，V18+→V7→V18→V1+；扇区B1，N=2，V1+→V18→V7→V1-；扇区B1，N=3，V1-→V7→V8→V1+；扇区B1，N=4，V1+→V8→V7→V8；扇区B2，N=1，V8→V9→V8→V2-。

按照矢量的作用时间和切换规则控制开关器件通断，可以在三相之间、整个基波周期内、任意整数脉冲数P下实现三电平SVPWM同步对称调制。

3 仿真结果及分析

搭建Matlab/Simulink 三电平NPC 逆变器仿真模型，仿真参数为：直流侧电压400 V，负载电阻10 Ω，电感5 mH。相电压波形如图3 所示。P=4时的平均开关频率（每周期总脉冲数与总开关器件数之比）为200 Hz，与相同平均开关频率下传统SVPWM进行仿真对比，谐波性能如图4所示。

图3 相电压波形Fig.3 Phase voltage waveforms

图4 电流谐波畸变率Fig.4 Current harmonic distortion

由图3可知，在指定脉冲数各种调制度下，输出电压脉冲数量和相位固定，且满足各项对称性质，符合给定脉冲数下的同步对称调制要求。

设线电压波形的周期函数为f（t），由于1/2周期对称、1/4周期对称特征，它在周期内同时具有偶函数f（t）=f（-t）和奇谐函数f（t）=-f（t±Ts/2）性质，故不含偶次谐波，只含有余弦项奇次谐波［8-9］，即2k±1；同时又由于三相对称，故不含有3 的倍数次谐波［10］，所以只含有6k±1 特征次谐波。由图4 可知，同步对称调制消除了相电流的3 的倍数次谐波和偶次谐波，与定性分析结论一致，另外，总谐波畸变率上较传统SVPWM 有明显改善。

图5 算法流程图Fig.5 Flow chart of the algorithm

图6 相电压与线电压实验波形对比Fig.6 Experimental waveforms comperison of phase voltage and line voltage

4 实验结果

以TMS320F28335 为控制器，搭建三电平NPC逆变器实验平台，对同步对称算法进行实验验证。算法流程图如图5所示。

具体实验参数为：直流侧电压80 V，负载为Y 型三相对称阻感负载，其中电阻10 Ω，电感5 mH，调制度为0.9，验证当N=3，P=4时的情况。

图6为同步对称调制下的相电压与线电压波形。由图6可知，电压波形输出脉冲稳定，满足同步对称要求，证明了实验算法正确性。

相同条件下与传统SVPWM 进行对比实验，二者的电流波形与谐波性能分别如图7和图8所示。低开关频率下传统SVPWM 输出电流波形畸变严重，谐波总畸变率较高。同步对称下电流波形正弦性良好，总畸变率由21.1%下降到10.4%，非特征次谐波被消除，优化效果明显，与理论和仿真结果一致，验证了同步对称调制的有效性。

图7 传统SVPWMFig.7 Traditional SVPWM

图8 同步对称SVPWMFig.8 Synchronization and symmetries SVPWM

5 结论

本文研究了三电平SVPWM 同步对称调制算法，给出了具体的矢量开关切换规律和算法实现步骤。仿真和实验结果表明，该算法可以在任意脉冲数下实现波形的同步、三相对称、1/2周期对称、1/4周期对称，可消除输出电流中的非特征次谐波，有效降低谐波总畸变率，适用于大功率低开关频率下三电平逆变器。算法易于实现。可进一步推广到更多电平数下的逆变器控制中。

［1］WU Bin. High-power Converters and AC Drives［M］. Hoboken：Wiley-IEEE Press，2006.

［2］袁庆庆，伍小杰，吴强，等.低开关频率下的不对称空间矢量脉宽调制［J］.电力电子技术，2013，47（5）：4-6，17.

［3］袁庆庆，伍小杰，吴强，等.三电平PWM 策略谐波性能的二重傅里叶分析［J］.中国矿业大学学报，2013，47（5）：859-865.

［4］马小亮.概述低开关频率PWM变频的问题及解决办法［J］.电气传动，2009，39（5）：3-9.

［5］Narayanan G，Ranganathan V T.Two Novel Synchronized Bus-Clamping PWM Strategies Based on Space Vector Approach for High Power Drives［J］.IEEE Trans.on Power Electronics，2002，17（1）：84-93.

［6］葛兴来，冯晓云.动车组牵引传动三电平逆变器SVPWM控制［J］.西南交通大学学报，2008，43（5）：566-572.

［7］张崇巍，范春明，张兴.中点电位平衡的三电平逆变器SVPWM简化算法及实现［J］.电气传动，2008，38（11）：37-48.

［8］Abdul Rahiman Beig，Narayanan G，Ranganathan RV T.Modified SVPWM Algorithm for Three Level VSI with Synchronized and Symmetrical Waveforms［J］. IEEE Transactions on Industrial Electronics，2007，54（1）：486-494.

［9］刘百芬，张利华.信号与系统［M］.北京：人民邮电出版社，2012.

［10］张雪原.SVPWM 调制下逆变器输出电压谐波分析［J］.电气传动，2010，40（7）：30-33.