基于自适应陷波器的分布式电源并网技术

殷桂梁，郭磊

（燕山大学电气工程学院，秦皇岛066004）

基于自适应陷波器的分布式电源并网技术

殷桂梁，郭磊

（燕山大学电气工程学院，秦皇岛066004）

分布式电源并网时要求与公共电网保持同频同相，传统的方法是使用锁相环提取公共电网电压的相角。为了提高控制系统的性能，该文提出了基于自适应陷波器的单相和三相并网控制系统，单相控制系统以电流控制为基础，参考电流的相角由ANF提取，三相控制系统采用PQ控制原理，电网电压的频率、幅值和相角由ANF检测。与基于锁相环的并网控制系统相比，文中的方法抗干扰能力强，最后通过仿真验证该文所提方法的快速性和准确性。

自适应陷波器；分布式电源；并网；频率变化；幅值变化；谐波

为了解决能源供求矛盾，改善地球环境，世界各国加快了对新能源的开发利用。分布式发电DG（distributed generation）是近年关注度较高的一种发电形式，所以相关技术在世界范围内得到广泛的发展[1-3]。分布式电源的形式多种多样，其中有一部分输出为直流电源或非工频交流电，它们必须经过并网逆变器并入公共电网，因此，逆变器的控制已经成为当前分布式发电研究的热点[4-8]。DG并网时需要保持与电网电压同频同相，所以逆变器控制系统中需要有提取电网电压相角的工具。最简单的相角提取方法是电压过零检测法[9]，但是，过零点只在电压的每半个周期出现一次，而且此方法不能有效地抑制谐波的干扰，因此当电压波动或存在谐波时，它的性能将会降低。后来有学者提出了滤波算法，基本原理是三相电压首先进行坐标变换，进而通过滤波器得到基频成分，最终得到相角[10]，这种方法的主要缺点是当电网频率变化或者电压不平衡时，性能会降低。在当前同步技术中，锁相环PLL（phase-locked loop）是使用最广泛的[11]。它主要由相位比较器、低通滤波器和压控振荡器组成。学者们不断地改进其中的相位比较器，进而得到了增强锁相环EPLL（enhanced PLL）[12]、移相锁相环QPLL（quadrature PLL）[13]、双二阶广义积分锁相环DSOGI-PLL（double second ordergeneral-ized integrator-PLL）[14]和同步参考坐标锁相环SRFPLL（synchronous reference frame-PLL）[15]。锁相环技术的主要缺点是对谐波的抗干扰能力不理想，频率追踪的速度较慢。文献[16]提出了自适应陷波器ANF（adaptive notch filter）用来检测信号的频率，能够把它引入分布式电源并网系统中，用来检测电网侧电压的相角。

本文提出将ANF的方法应用于分布式电源并网控制系统中，用它取代锁相环。在单相并网系统中，设计了基于ANF的电流控制系统，三相并网系统中，设计了基于ANF的PQ控制系统。与基于锁相环的并网系统比较，本文提出的方法在电网电压处于非标准情况时也能可靠地工作。

1 ANF的基本原理

1.1 ANF的基本原理

文献[16]提出的ANF能够快速准确地跟踪输入信号的频率变化，可以得到输入信号的正交变换，幅值、频率等信息，在频率检测，序分量分解，谐波检测等领域得到了广泛应用。

设任一周期信号为

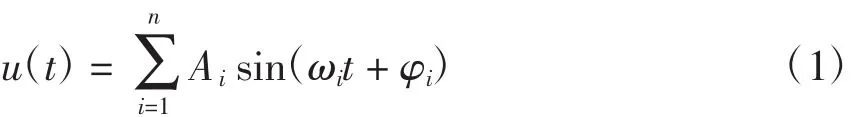
自适应陷波器的动态方程为

式中：u（t）为输入信号；γ和ζ分别为ANF的参数；x为中间变量；θ为输入信号频率的估计值。当输入信号为单一频率的正弦波时，ANF具有唯一的局部收敛根轨迹[16]，即

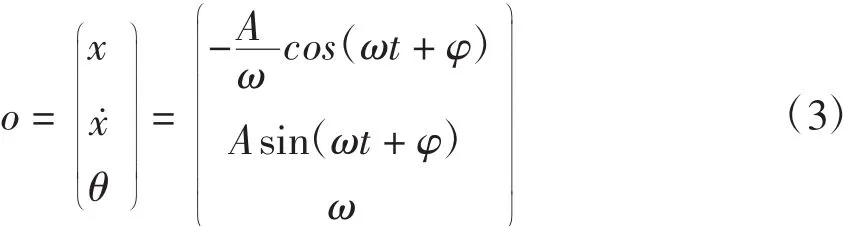
1.2 ANF提取基波和谐波分量

当信号含有谐波时，动态微分方程[16]变为

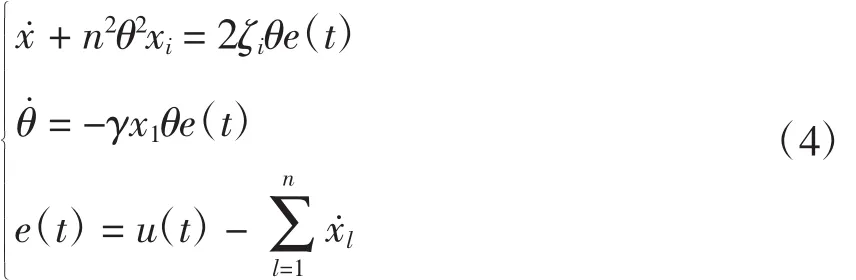
对ANF的结构进行修改，其中主ANF用来检测基频成分的信息，副ANF可以检测各个谐波的信息，每次谐波都有与其对应的ANF。提取基波和5次谐波分量的结构如图1所示。ζi为第i个ANF的参数，θ为输入信号基频频率的估计值。

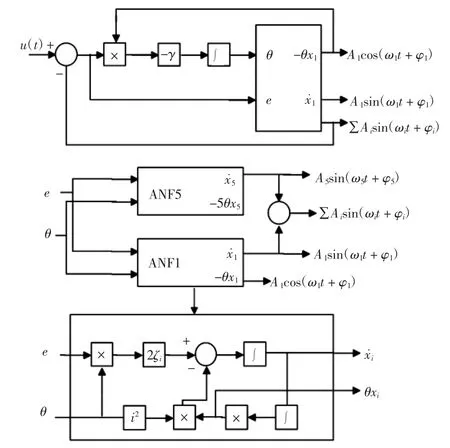
图1 ANF提取基波和5次谐波分量Fig.1 Extraction of fundamentaland 5th harmonic based on ANF

2 基于ANF的单相并网系统

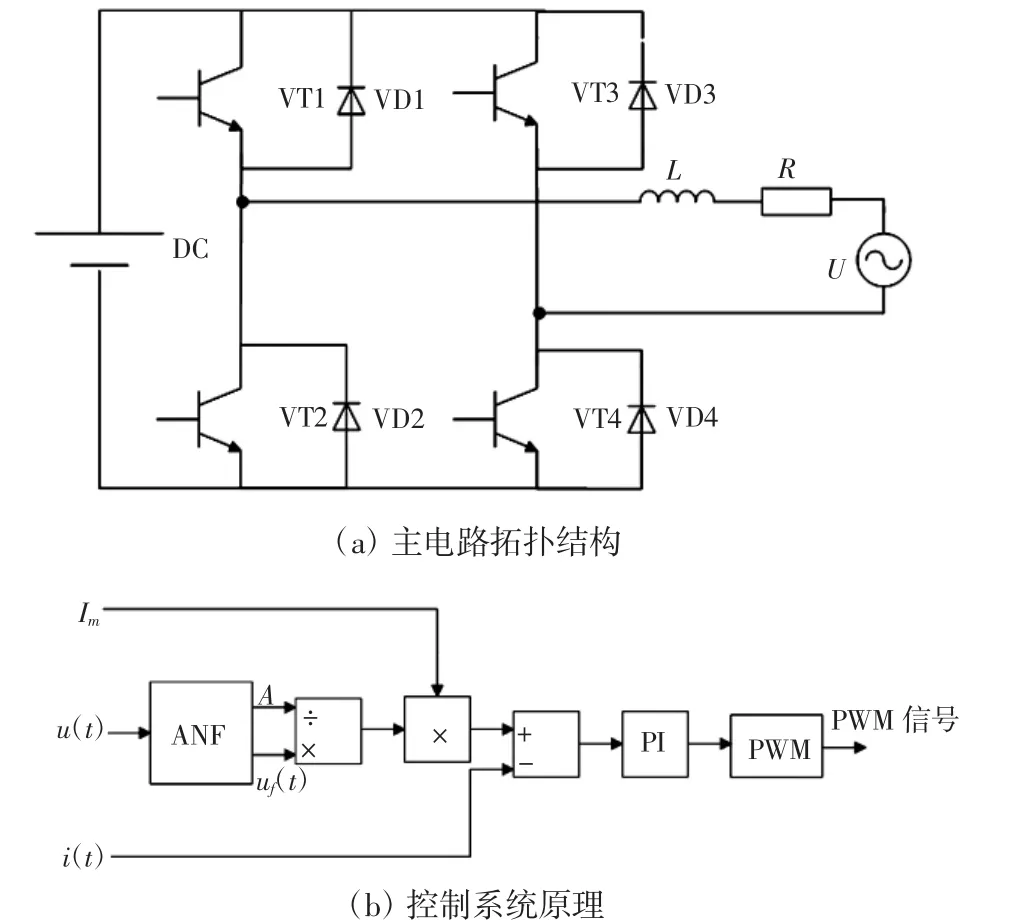
图2 单相并网系统Fig.2 Single phase grid-connected system

分布式电源的单相并网主电路结构如图2（a）所示，电感用于滤除由于开关动作引起的高次谐波电流，使并网输出电流是与电网电压同频同相的正弦波。本节提出的逆变器控制系统采用电流控制，具体的原理如图2（b）所示，其中u（t）为电网电压，Im为并网电流的幅值，i（t）为并网电流，A为输入信号幅值，uf（t）为输入信号的基频分量，当输入信号为单一频率时，即为原样输出。电网电压信号通过ANF得到其原样输出和幅值，将两者相除可得到电网电压的三角函数值，同时通过频率计算相角，进而计算三角函数值，然后将两者相比。本节提出的方法能够整体获得相角的三角函数值，减小了误差，设定的并网电流的幅值与三角函数值相乘即可得到并网电流的参考值，它与当前并网电流做差依次送入PI调节器和PWM发生器产生PWM信号，进而控制逆变器。

3 基于ANF的三相并网系统

三相分布式电源并网时通常使用PQ控制，这样能够提高能量利用效率[17]。设计的分布式电源三相并网控制系统如图3（a）所示，控制子系统由图3（b）、（c）和（d）给出。PQ控制的基本原理是通过P和Q的设定值计算出参考有功电流和参考无功电流，然后调节并网电流的有功成分与无功成分跟踪参考值。

其中，ANF单元的主要功能是提取电网侧电压的相角信息，得到相角的三角函数值，同时得到并网电流的d轴和q轴分量；功率控制单元的主要功能是通过设定的PQ值，计算并网电流的d轴和q轴分量的参考值；PWM信号单元的主要功能为将当前并网电流的d轴和q轴分量与d轴和q轴分量的参考值的差别送入PI控制器，进而控制PWM信号发生器产生响应的脉冲信号。

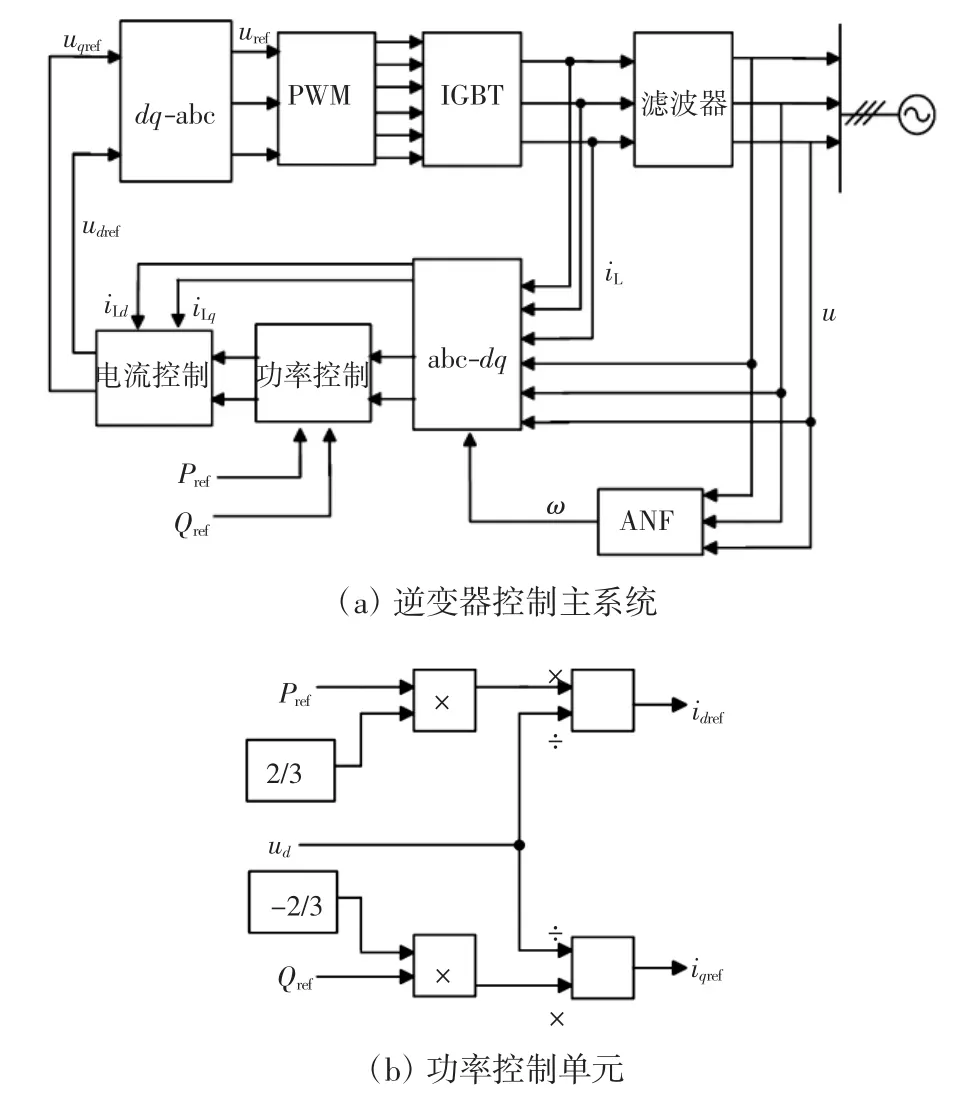
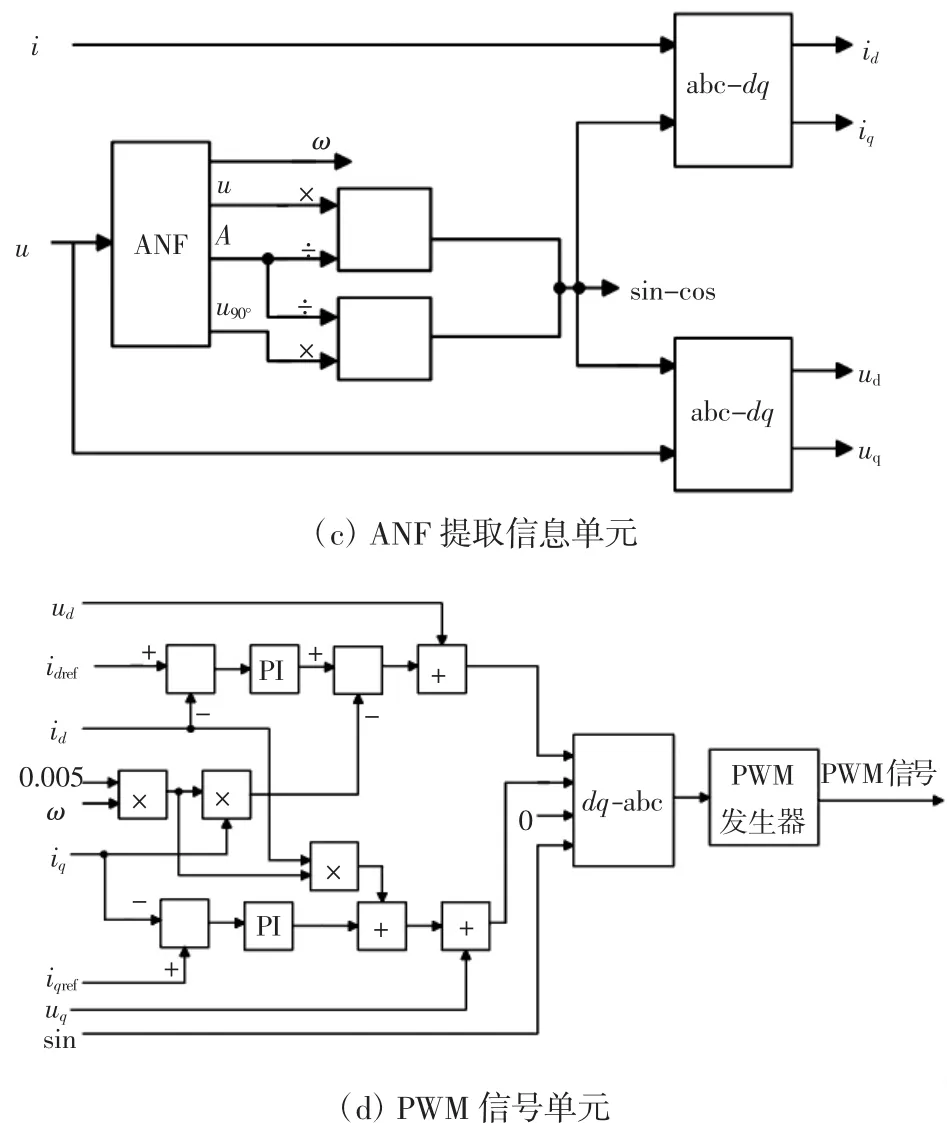
图3 三相并网系统Fig.3 Three phase grid-connected system

4 仿真分析

4.1 单相并网系统的仿真

用Matlab/Simulink建立了系统仿真模型，由于ANF检测的幅值都是从零开始，所以在仿真过程中需添加一个阶跃函数，以保证在仿真开始时不会出现奇异点。为了全面验证本文提出的基于ANF的单相并网控制系统，分别在电网电压为标准情况，电压幅值发生变化，电压频率变化，电压含有谐波等情况下仿真。直流电源电压为440 V，电网电压的标准情况为u=220sin（100πt），并网电流的幅值Im=10 A，逆变器的滤波电感L= 0.003 H，电阻R=0.1Ω，PI控制器的kp=2，ki= 512，ANF的参数γ=800，ζ=1.2。

4.1.1 标准情况

图4为基于ANF控制系统的分布式电源发出的功率波形，图5为基于PLL控制系统的分布式电源发出的功率波形，通过对比可以看出，在标准情况下，两种方法都能使并网电流基本达到与电网电压同频同相。

4.1.2 电压幅值发生变化

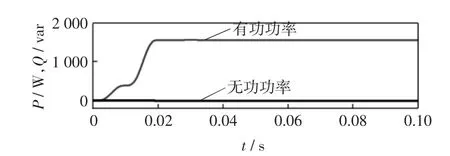
图4 基于ANF控制系统的分布式电源发出功率波形Fig.4 Power waveformsof DG based on ANF controlsystem

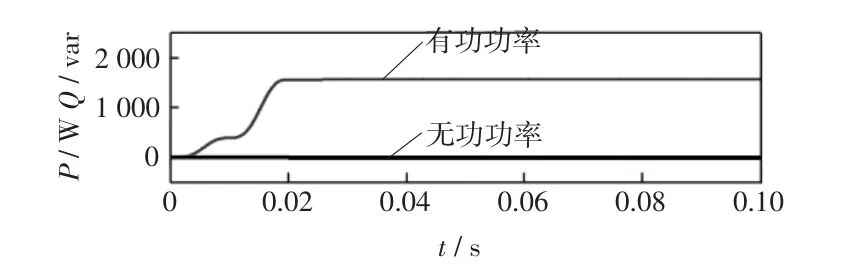
图5 基于PLL控制系统的分布式电源发出功率的波形Fig.5 Power waveform sof DG based on PLL controlsystem

当t=0.1 s时，电压幅值增大10%，当t=0.3 s时，电压幅值恢复为初始值。图6为基于ANF的并网系统中分布式电源发出的功率波形，当幅值变化时，无功功率会在1.5个周期内波动，且波动值较小，图7为基于PLL的并网系统中分布式电源发出的功率波形，当幅值变化时，无功功率会在3~ 4个周期内波动，且波动较大。主要原因是在幅值变化的情况下，ANF提取电压的相角信息比PLL的精度要高。

图6 基于ANF控制系统的分布式电源发出功率波形Fig.6 Power waveform sof DG based on ANF controlsystem

4.1.3 电压频率变化

当t=0.2 s时，电网电压频率增大0.5 Hz，当t=0.5 s时，电网频率恢复为初始值，即50Hz。图8为基于ANF的并网系统中分布式电源发出的无功功率波形图，当电网电压频率变化时，无功功率会在1个周期内波动，且幅度较小，图9为基于PLL的并网系统中分布式电源发出的无功功率波形，当电网电压频率变化时，无功功率会在7个周期内波动，且幅度较大。主要原因是基于ANF的并网系统具有更好的频率适应性。

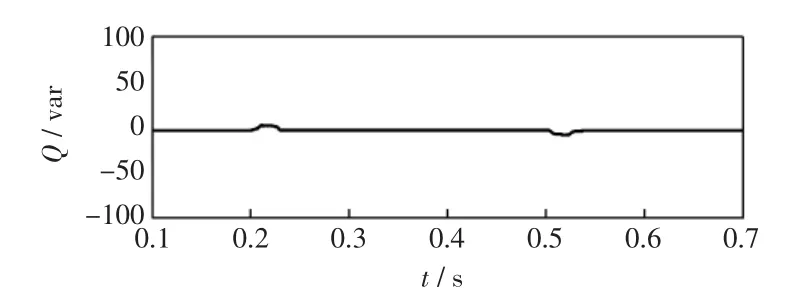
图8 基于ANF控制系统的分布式电源发出的无功功率Fig.8 Reactive power of DG based on ANF controlsystem

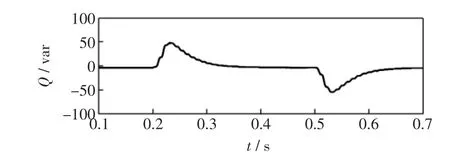
图9 基于PLL控制系统下的分布式电源发出的无功功率Fig.9 Reactive power of DG based on PLL controlsystem

4.1.4 电压含有谐波

当t=0.2 s时，电压突然含有40%的5次谐波，30%的7次谐波，t=0.4 s时，谐波消失，电压恢复为标准情况。图10为基于ANF控制系统的分布式电源发出的无功功率波形，从图中可以看出，基于ANF的并网系统中，分布式电源发出的无功功率会在1.5个周期内波动，即1.5个周期后并网电流将会与电网电压同频同相，从图11看出，基于PLL的系统中，无功功率会波动6个周期，且波动值较大。主要原因是含有谐波的情况下，ANF依然能够快速准确的检测相位信息，而PLL的响应时间变长，且精度下降。

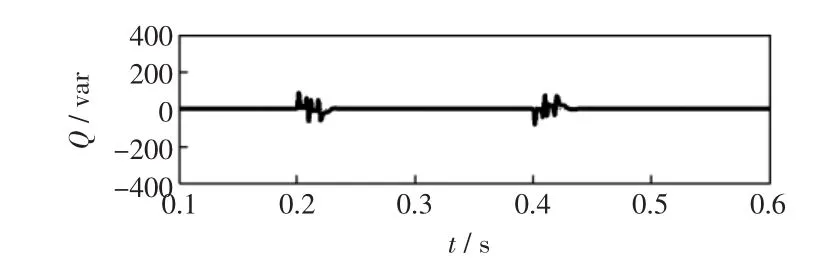
图10 基于ANF控制系统的分布式电源发出的无功功率Fig.10 ReactivepowerofDG based on ANFcontrolsystem

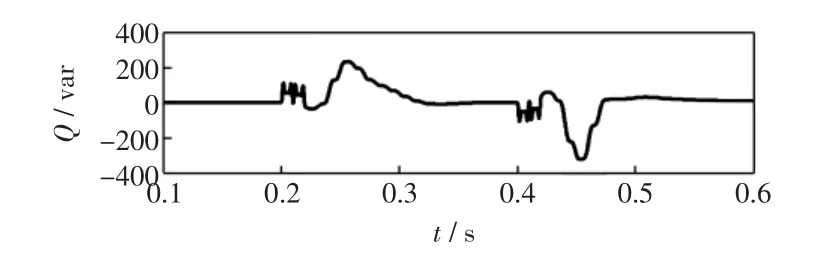
图11 基于PLL控制系统的分布式电源发出的无功功率Fig.11 Reactivepower ofDG based on PLL controlsystem

4.2 三相并网系统的仿真

用Matlab/Simulink建立了系统仿真模型，同样在幅值检测处添加一个阶跃函数，以保证在仿真开始时不会出现奇异点。设三相系统为平衡系统，即不存在负序和零序分量，分别在电网电压稳定、和电网电压频率变化两种情况下仿真，为了便于比较，仿真结果全部取A相的波形。P和Q分别设置为30 kW和0 var。直流电源电压为600 V，电网电压的标准情况为u=2202sin（100πt），LC滤波器的L=5×10-3H，C=1×10-5F，R=0.1Ω，ANF的参数γ=800，ζ=1.2。

4.2.1 标准情况

图12为基于ANF的并网系统中A相发出的功率波形，图13为基于PLL的并网系统中A相发出的功率波形，在标准情况下，分布式电源发出的无功功率均为150 var左右，有功功率为10 kW，基本达到了并网电流与电网电压同频同相的要求。

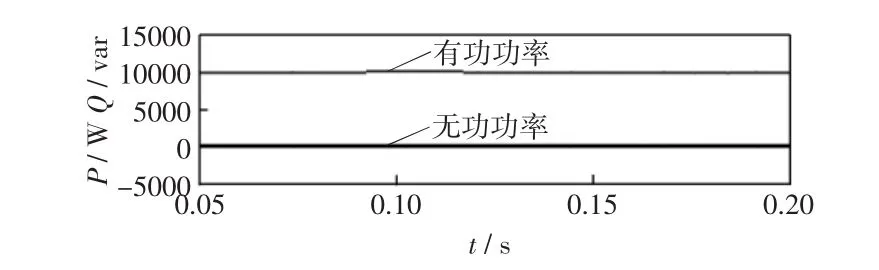
图12 基于ANF控制系统的分布式电源发出功率波形Fig.12 Power waveformsof DG based on ANF control system

图13 基于PLL控制系统的分布式电源发出功率波形Fig.13 Power waveformsof DG based on PLL controlsystem

4.2.2 频率发生变化

当t=0.1 s时，电网电压频率增大为51Hz，图14为基于ANF的并网系统中A相发出的功率波形，当频率变化时，无功功率会在两个周期内发生明显的波动，最大波动值为240 var，图15为基于PLL的并网系统中A相发出的功率波形，从图中可以看出，当频率变化时，无功功率会在8个周期内发生明显的波动，最大波动值为540 var，这表明，在电网频率变化的情况下，基于ANF的三相并网系统的性能优于基于PLL的并网系统。

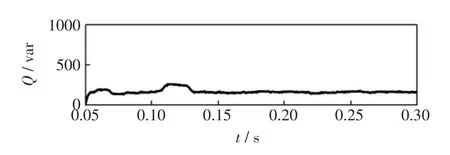
图14 基于ANF控制系统的分布式电源发出的无功功率Fig.14 Reactivepower ofDG based on ANF controlsystem

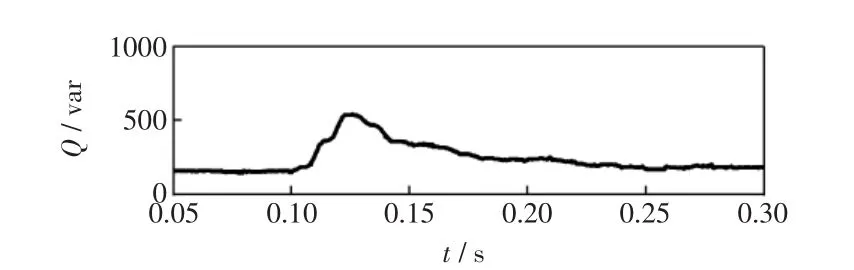
图15 基于PLL控制系统的分布式电源发出的无功功率Fig.15 Reactivepower ofDG based on PLL controlsystem

5 结语

本文提出了基于ANF的单相和三相并网控制系统，其中，单相并网控制系统为基于ANF的电流控制系统，三相并网控制系统为基于ANF的PQ控制系统，分别与对应的基于PLL的控制系统的性能进行对比，可以得到如下结论：在电网电压为标准情况时，本文提出的方法能够可靠地并网，在电网电压为非标准情况时，本文提出的方法比基于PLL的控制系统具有更高的精度和更快的响应速度。

[1]Kramer W，Chakraborty S，Kroposki B，et al.Advanced power electronic interfaces for distributed energy systems [R].Battelle：MidwestResearch Institute，2008.

[2]崔金兰，刘天琪（Cui Jinlan，Liu Tianqi）.分布式发电技术及其并网问题研究综述（Distributed generation and its grid interconnection issue）[J].现代电力（Modern Electric Power），2007，24（3）：53-57.

[3]王成山，李琰，彭克（Wang Chengshan，LiYan，Peng Ke）.分布式电源并网逆变器典型控制方法综述（Overview of typical controlmethods for grid-connected inverters of distributed generation）[J].电力系统及其自动化学报（Proceedingsof the CSU-EPSA），2012，24（2）：12-20.

[4]丁明，王敏（DingMing，WangMin）.分布式发电技术（Distributed generation technology）[J].电力自动化设备（Electric Power Automation Equipment），2004，24（7）：31-36.

[5]刘凤君.现代逆变技术及应用[M].北京：电子工业出版社，2006.

[6]刘凤君.正弦波逆变器[M].北京：电子工业出版社，2002.

[7]王兆安，黄俊.电力电子技术[M].北京：机械工业出版社，2000.

[8]徐德宏.电力电子系统建模及控制[M].北京：机械工业出版社，2005.

[9]Blaabjerg F，Teodorescu R，Liserre M，et al.Overview of controland grid synchronization for distributed powergeneration systems[J].IEEE Trans on Industrial Electronics，2006，53（5）：1398-1409.

[10]Lee Sang-Joon，Kim Hyosung，Sul Seung-Ki，etal.A novel controlalgorithm forstatic series compensatorsby use of PQR instantaneous power theory[J].IEEE Trans on Power Electronics，2004，19（3）：814-827.

[11]Hsieh Guan-Chyun，Hung James C.Phase-locked loop techniques-a survey[J].IEEE Trans on Industrial Electronics，1996，43（6）：609-615.

[12]Karimi-GhartemaniM，IravaniMR.A nonlinear adaptive filter for online signal analysis in power system：applications[J].IEEE Trans on Power Delivery，2002，17（2）：617-622.

[13]KarimiH，Karimi-GhartemaniM，IravaniMR.Estimation of frequency and its rateof change forapplications in power systems[J].IEEE Trans on Power Delivery，2004，19（2）：472-480.

[14]Rodriguez P，Teodorescu R，Candela I，etal.New positivesequence voltage detector for grid synchronization of power converters under faulty grid conditions[C]//IEEE Power Electronics Specialists Conference.Jeju，South Korea：2006.

[15]Limongi LR，BojoiR，Pica C，etal.Analysisand comparison of phase locked loop techniques for grid utility applications[C]//Fourth Power Conversion Conference.Nagoya，Japen：2007.

[16]MojiriM，BakhshaiA R.Estimation ofn frequencies using adaptive notch filter[J].IEEE Trans on Circuit and Systems II，2007，54（4）：338-342.

[17]杨文杰（YangWenjie）.光伏发电并网与微网运行控制仿真研究（Simulation and Research of Grid Connected Photovoltaic Generation and Microgrid Operation Control）[D].成都：西南交通大学电气工程学院（Chengdu：Schoolof Electrical Engineering of Southwest Jiaotong U-niversity），2010.

Grid-connection Technology for Distributed Generation Based on Adaptive Notch Filter

YINGuiliang，GUO Lei
（SchoolofElectric Engineering，Yanshan University，Qinhuangdao066004，China）

In general，grid-connected distributed generationmustbe synchronized with the utility grid.The phase angle ofgrid voltage isdetected by phase locked loop（PLL）in traditionalcontrolsystem.In order to improve the performance of control system，in this paper，single and three phase grid-connected controlmethods based on adaptive notch filter（ANF）are proposed.Single phase grid-connected controlmethod is based on current control and the phase angle of reference current is extracted by ANF.Three phase grid-connected control approach isbased on PQ control.The frequency，amplitude and phase angle of the voltage is detected by ANF.Compared with the grid-connected control system based on PLL，the proposedmethod offers high insensitivity to the grid disturbance.Finally，the rapidity and accuracy of the proposedmethod isverified by simulation.

adaptive notch filter（ANF）；distributed generation；grid-connected；frequency variation；amplitude variation；filter

TM711

A

1003-8930（2015）04-0067-06

10.3969/j.issn.1003-8930.2015.04.012

殷桂梁（1964—），男，博士，教授，研究方向为配电网自动化和微电网运行与控制。Email：glyin@ysu.edu.cn

2013-04-22；

2013-06-07

郭磊（1987—），男，硕士研究生，研究方向为电网信息提取和微电网运行与控制。Email：jiuyinhuanpei@163.com