计算架空线路分布参数的新方法

焦彦军，于江涛，王增平

（新能源电力系统国家重点实验室（华北电力大学），北京102206）

计算架空线路分布参数的新方法

焦彦军，于江涛，王增平

（新能源电力系统国家重点实验室（华北电力大学），北京102206）

提出一种考虑土壤电阻率影响的架空输电线路分布参数计算新方法。介绍和分析了Carson公式和Dubanton公式，提出用函数代替的方法简化Carson校正项来避免Carson公式计算困难、Dubanton公式误差较大的问题，总结出一种计算精度较高的架空线路分布参数计算新方法。误差分析表明，该方法的计算公式简单、计算值连续、计算结果较精确。该方法可替代Dubanton公式进行相应的计算和分析，在电力系统分析、仿真及计算中具有很强的实用价值。

架空线路；分布参数；Carson公式；Dubanton公式；Carson校正项；函数代替

架空输电线路的串联电阻、电抗及对地电容、电导总是沿线路分布的，且线路的串联电阻、电抗易受土壤电阻率影响[1-7]。线路长度与信号波长相比不能忽略时，线路中信号的行波传输特征较明显[15-16]，系统仿真、分析及计算需采用分布参数才能取得较理想的结果。一种高精度、快速的、考虑土壤电阻率影响的线路参数算法对电力系统的相关研究具有重大的意义。

架空线路的分布参数中电抗及电阻常采用Carson公式[1-2]、简化Carson公式[3]或Dubanton公式[3-4]进行计算，3种方法对土壤电阻率影响的处理方式不同，文献[4-8]也对此进行了一定的分析和讨论。简化Carson公式及Dubanton公式的形式简单，但误差较大，目前仍认为Carson公式计算结果较为精确、并广泛用于各种计算软件中。Carson公式校正项中含有第二类Bessel函数Y1（x）及Struve函数H1（x）[1]，表达式不利于用于公式推导，其算法在高、低频时的计算方法不同[2-3，8-9]，算法切换处附近的计算值误差较大、结果不连续，对相关研究也带来一定的影响。

本文根据Carson校正项里的函数特点，提出利用易积分的函数取代其中的原函数，得到了较为精确的校正项计算结果，并总结出一种架空线路分布参数计算的新方法。误差分析的结果表明：新方法的校正项计算结果具有较好的精度，其实部、虚部、模值最大相对误差均小于Dubanton公式的最大误差，可替代Dubanton公式进行相应的计算和分析。新方法的计算公式简单、计算值连续、计算结果较精确，具有很强的实用价值。

1 Carson公式与Dubanton公式

1.1 Carson公式

1926年，Carson、Pollaczek等提出了考虑土壤电阻率的架空导线阻抗计算方法，Carson还提出了相应的级数算法，该算法经研究、补充后成为目前应用最广泛的架空线路参数算法[1-3]。

两导体k、l及其镜像k′及l′的相对位置如图1所示，若土壤电导率为σ、真空磁导率为μ0、信号的角频率为ω，则导体k的自阻抗Zs可用式（1）计算，导体k、l间的互阻抗Zm可用式（2）计算，式（1）（2）即为Carson公式。

图1 两导线相对位置示意Fig.1 Diagram of two conductorsconfiguration

式中，省略了导体内阻抗，实际计算中需补充。Js与Jm为Carson校正项，用于解决非零的土壤电阻率对线路参数的影响，计算方法为

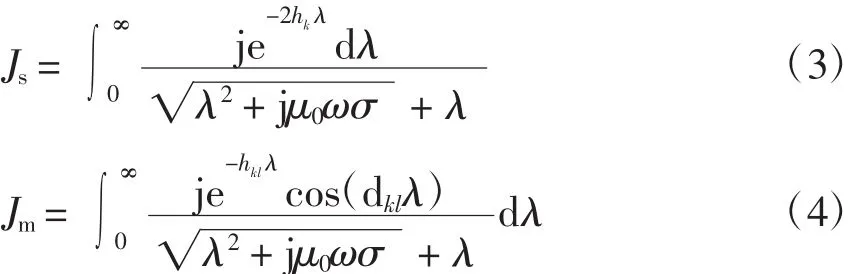
式中，hkl=hk+hl。

式（3）和式（4）可进行简化，式（3）可写为

并定义函数F（s），式（4）则可写为

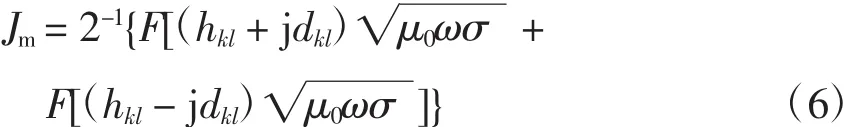
式（5）和式（6）中函数F（s）变量s实部始终大于0，即Re（s）>0、π/2>Arg（s）>-π/2，此时函数F（s）的积分结果如式（7）所示。式（7）中Y1（x）为第二类Bessel函数、H1（x）为Struve函数。

式（5）式（6）无法直接得出精确的计算结果，可采用复化Simpson法近似计算式（3）和式（4），但计算量大、计算复杂。文献[1]为式（3）和式（4）给出了相应的级数表达式，经相关人员完善形成了易于计算的形式[8-9]，并得到广泛使用[2]。

Carson公式适合用于需要精确计算值的环节、不适合应用于公式推导，Carson算法的计算结果不连续，这均将对相应的分析和研究带来影响。Carson算法中仅保留一次项时形成的表达式即为简化Caroson公式[3]，简化Carson公式有较简单的表达形式，但存在较大的误差。

1.2 Dubanton公式

Dubanton公式也称为复穿透距离法[3]，该方法通过增加一个复数埋深来解决土壤电阻率、磁导率变化对架空线路参数的影响[3-4]，所增加的复距离和Dubanton公式分别为

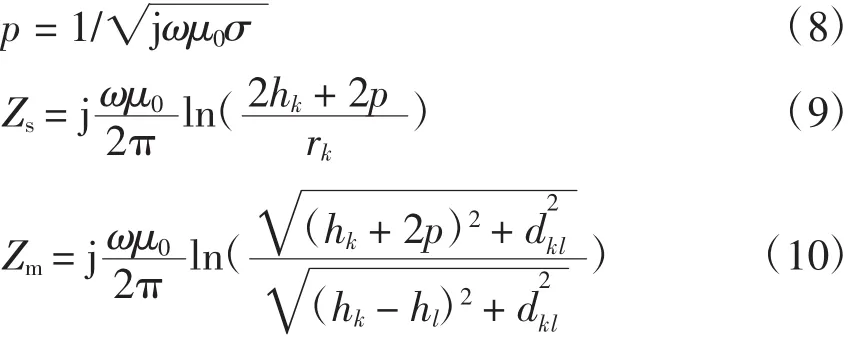
对比式（1）和式（2）与式（9）和式（10）易知，Dubanton公式将Carson校正项Js与Jm分别简化为

Dubanton公式的计算相对简单、方便，但文献[4]在推导复穿透距离时所选用的剖面具有代表性，但不能体现电磁场沿导线断面分布中的差异，计算结果将总存在一定的误差。Dubanton公式的表达形式简单、计算结果连续、计算精度介于Carson及简化Carson公式之间，可用于公式推导，但其计算精度仍存在提升的可能。

2 计算架空线路分布参数的新方法

Carson公式的架空线路参数计算结果较为准确，而Carson算法采用了级数叠代、不适于公式推导，其算法切换位置可能存在较大误差；若采用复化Simpson法进行计算，计算量大、计算复杂、应用面小。简化Carson公式及Dubanton公式虽具有简单的形式，但误差较大。因此一种表达形式简单、计算量低、计算精度较高的架空线路参数的计算方法具有很强的实用价值。

文献[4]提出Dubanton公式相当于用函数替代简化了Carson校正项，这为Carson公式的简化提供了思路。

研究发现，当Re（s）>0时

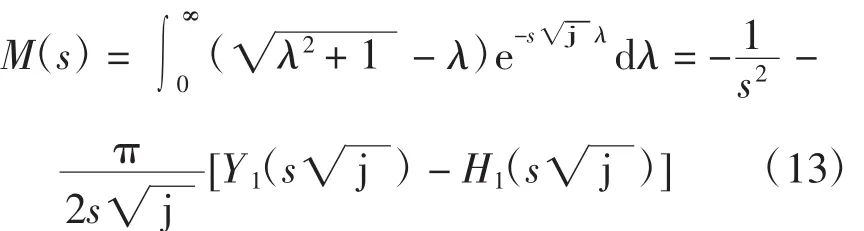
始终成立。对比式（7）可知，Re（s）>0时M（s）=F（s）成立。

定义函数F1（λ）、F2（λ）、F3（λ）为

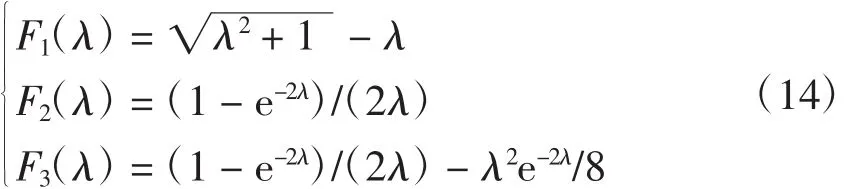
函数F2（λ）、F3（λ）与F1（λ）的差别见图2。

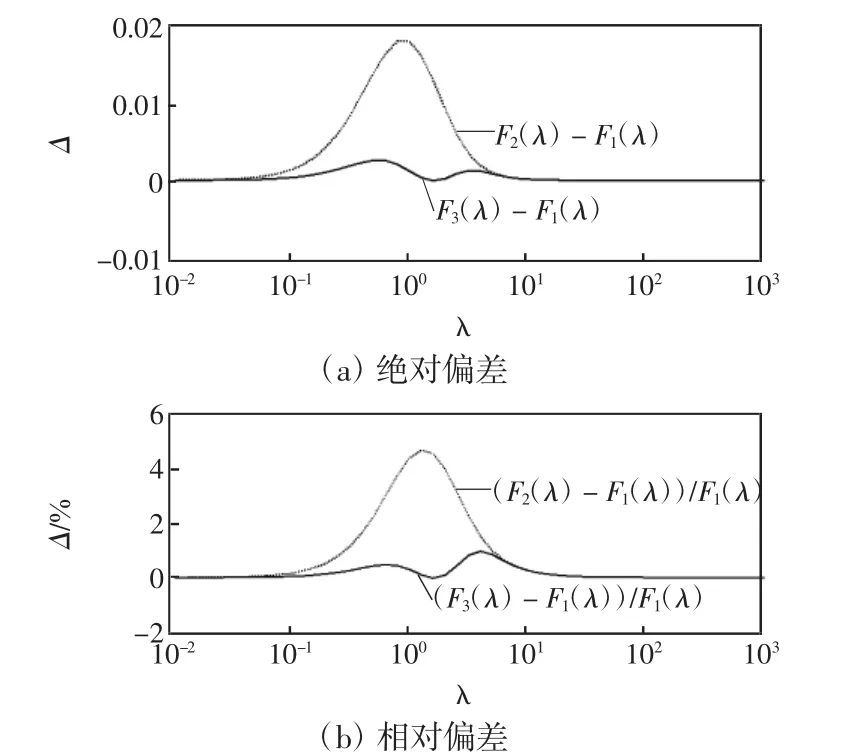
图2 函数值的差别Fig.2 Difference of function values

文献[4]用函数F2（λ）在式（13）中替代函数F1（λ）推导出Dubanton公式。由图2知，采用函数F3（λ）替代函数F1（λ）时形成的计算方法性能应优于Dubanton公式。

用函数F3（λ）替代式（13）中的函数F1（λ），导出式在Arg（s）<π/4时可积分、结果为

导出式在π/4≤Arg（s）<π/2时难以直接计算，可按

进行函数替换，结果与式（15）相同。

由式（15）和式（16），Carson校正项中自、互阻抗部分可分别简化为

则Carson公式中自、互阻抗计算可分别简化为

即为计算架空线路分布式参数的新方法。

从图2的函数值对比易知，新方法计算结果的最大误差应小于Dubanton公式计算结果的误差；由式（15）和式（16）易知，新方法的计算结果在θ＜π/4时具有极高的精度，但在θ＞π/4时计算结果的最大误差将随θ增大而增大。

3 误差分析

3.1 模型参数

本文以图1所示的2导线系统进行误差计算与分析，基本参数为：两线对地距离均为20m，土壤电阻率为200Ω·m，线水平间距由图1中θ决定，导线为直径2.5 cm的单根导线。

3.2 基准值

式（5）~式（7）是Carson校正项的精确表达形式，通常采用Carson算法[1-2]进行近似计算。Carson算法用式（21）的值来切换算法，算法切换处附近计算结果不连续（文献[2]中切换值为5），计算值在α介于3~5之间总存在较大误差。

式（21）用于导线k的自阻抗计算时dkl为0、hkl为2hk。

随着算法的发展，Y1（x）与H1（x）的算法日趋成熟[13-14]，使直接计算Y1（x）与H1（x）成为可能，如Mathematica就提供了相应函数。计算表明：α介于1~10之间时，直接计算的结果与用复化Simpson法计算式（3）和式（4）的结果基本吻合。但直接计算也存在一定问题，Y1（x）与H1（x）的差占其自身比例过小时，算法本身的误差可能导致计算结果出现较大偏差，计算值将发生摆动。

计算结果对比表明：两种计算结果均不能精确的描述式（5）和式（6）；两种结果在α等于1及10时基本相同，参见图3（a）、（b）；α介于1~10之间时，两者总存在误差（如α介于3~5之间），此时Carson算法的结果存在突变，而直接计算的结果更平滑、接近用复化Simpson公式计算的结果，参见图3（c）（图3（c）中Carson算法切换时α为3）。

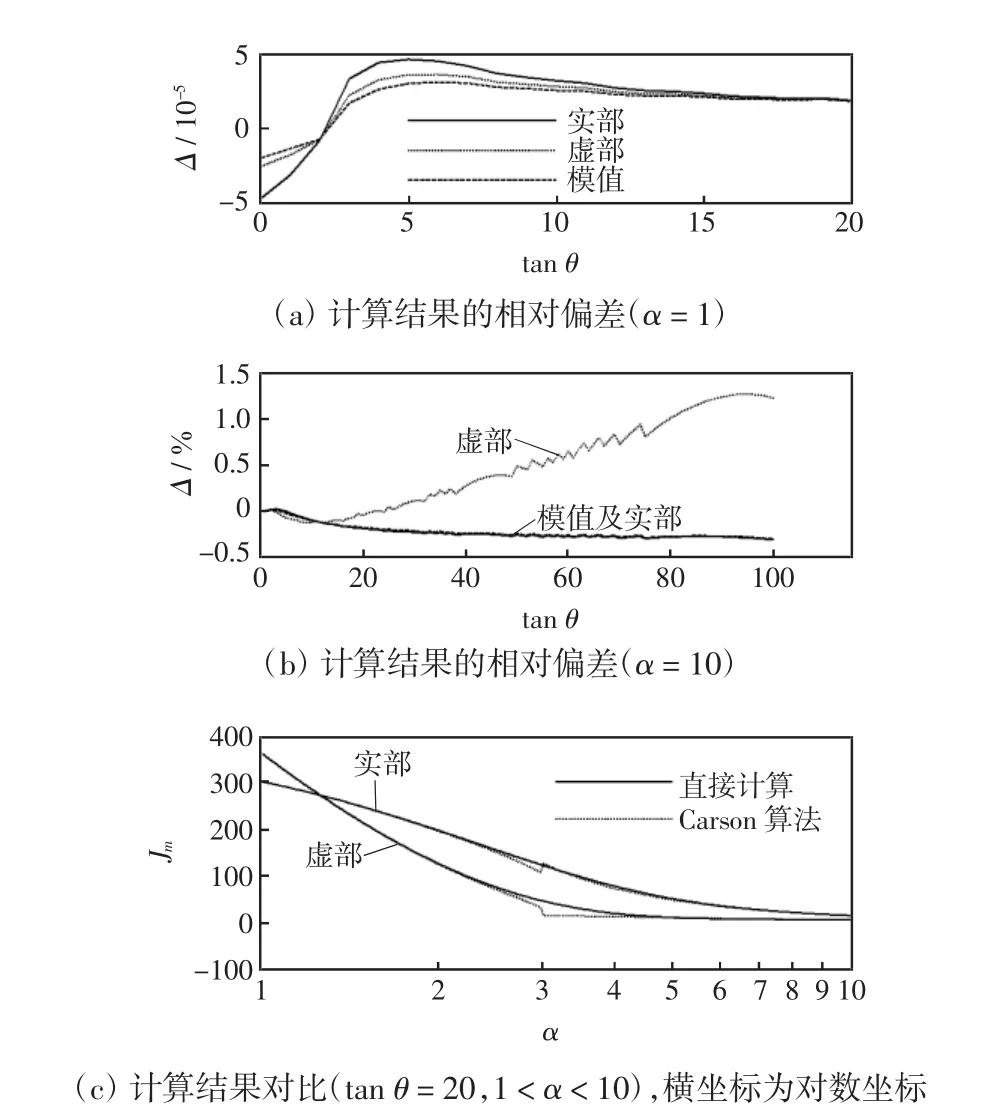
图3 计算结果的对比Fig.3 Comparison of the calculation results

由此，本文选用混合计算结果作为基准数据，其校正项在α介于1~10时选用直接计算结果、α为其他值时选用Carson算法的计算结果。

3.3 误差对比与分析

1）最大相对误差的对比

tanθ不大于100时，用新方法及Dubanton公式分别进行计算，两种方法计算结果校正项最大相对误差的模值对比如图4所示，总阻抗最大相对误差的模值对比如图5所示。

图4 校正项的最大相对误差模值Fig.4 Maximum nodulusof relativeerror in correction terms

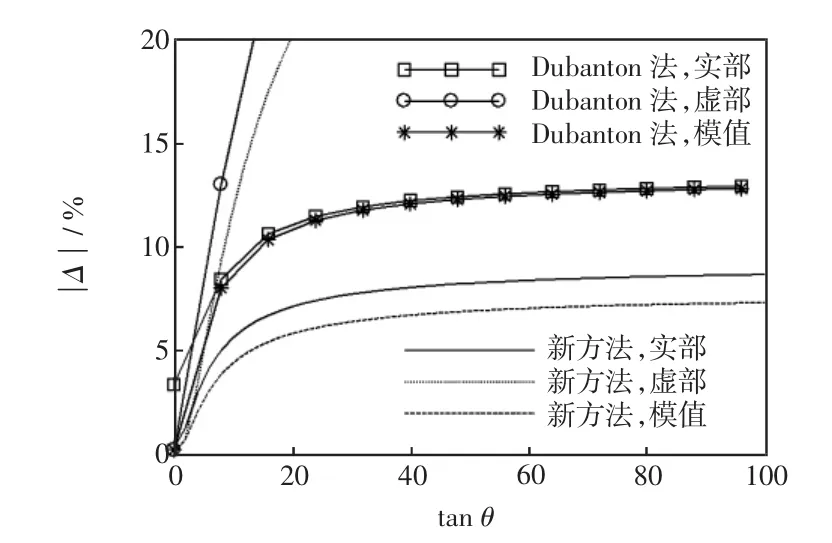
图5总阻抗的最大相对误差模值Fig.5 Maximum modulusof relative error in total impedance

图4 和图5表明：

（1）两种方法计算结果的最大相对误差均随tanθ增大而增大，其中实部及模值的最大相对误差变化逐渐变慢，虚部的最大相对误差增长极快、但其绝对误差较小、对模值相对误差的影响极小。

（2）新方法自阻抗计算的精度较高，校正项的实部、虚部、模值最大相对误差分别为0.294%、0.200%、0.214%，远小于Dubanton公式的计算误差。

（3）在tanθ<1时，新方法具有极高的计算精度，互阻抗计算结果实部、虚部、模值的最大误差分别不超过0.56%、0.24%、0.25%。

（4）当tanθ>10时，图4中校正项的最大相对误差和图5中总阻抗的最大相对误差几乎相等，说明此时线路互阻抗中校正项所占比例较大、对计算精度影响较大。

（5）新方法计算结果的最大相对误差总是小于Dubanton公式。如tanθ为100时新方法计算结果的实部、模值的最大误差分别为8.66%与7.31%，而Dubanton公式的相应误差接近13%。

2）新方法计算总阻抗的相对误差

根据图4和图5所示的计算结果，选择较有代表性、方便比较的角度进行计算，新方法计算的总阻抗模值、实部及虚部相对误差如图6所示。图6中各曲线的tanθ数值标记在该曲线的最大模值附近。

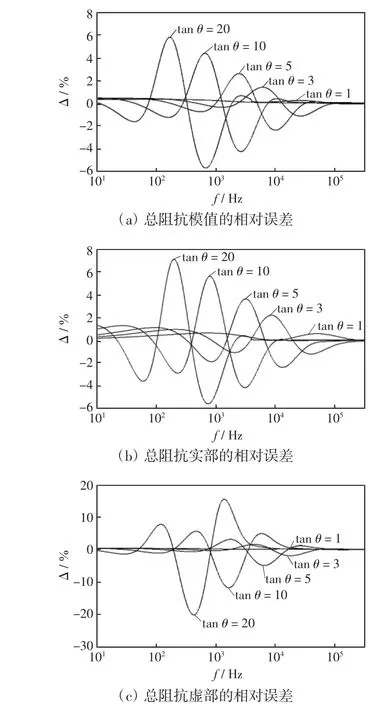
图6总阻抗的相对误差Fig.6 Relative error in the total impedance

图6 表明：

（1）新方法计算结果的最大误差随tanθ增大而不断增大的同时，发生位置也不断向低频发展。根据图6计算结果中的最大误差分布及式（21）易推知，tanθ>3时计算结果的最大误差发生频率大致与1+tan2θ成反比。

（2）当tanθ<20时，计算结果中误差较大的部分主要集中在（102~105）Hz之间，其实部、虚部、模值误差小于7.11%、20.20%、5.82%，但小于1Hz的数据仍能保持一定的精度。

（3）计算结果中50Hz数据的各部分随tanθ的增加而发生变化，但tanθ<20时50Hz的数据仍能保持较高的精度，其实部、虚部、模值误差分别小于3.40%、1.40%、1.64%。

3.4 计算方法的性能分析

常规单回或同杆多回架空线路的架设参数通常满足tanθ<1，此时新方法自、互阻抗计算结果的实部、虚部及模值均具有较高的精度，计算结果能满足大部分仿真及计算的需要。

在平行线路的互阻抗计算中：tanθ不大时（小于20），该方法的计算结果能保证较高的精度，误差较大部分主要集中在102~105Hz之间，50Hz数据仍能保持较高的精度；当tanθ较大时，线路参数计算结果通常用于计算线路之间的相互干扰，此时该方法计算结果的实部和模值仍能具有一定的精度、但虚部误差较大，线路间相互干扰的幅值计算结果仍能保持一定的精度。

架空线路分布参数计算新方法的公式简单、计算结果连续、精度高于Dubanton公式，可替代Dubanton公式进行相应的分析、计算，在电力系统分析、仿真及计算中均具有较强的应用价值。

4 结语

本文利用函数替代法简化了Carson公式，提出了一种架空线路分布式参数计算的新方法，该方法也可看作为Dubanton公式的改进，具有计算公式简单、计算结果连续、计算精度较高的优点。该方法的计算精度高于Dubanton公式的计算精度，可替代Dubanton公式参与相应的分析与计算，在电力系统计算及仿真中均具有较强的应用价值，但其计算精度是否可继续提高还有待进一步的研究。

[1]Carson J R.Wave propagation in overhead wires with ground return[J]．Bell System Technical Journal，1926，5（4）：539-554．

[2]Dommel HW．EMTPTheory Book[M]．Vancouver：Microtran Power System AnalysisCorporation，1992．

[3]Beaty HW．电力计算手册[M]．北京：中国电力出版社，2007．

[4]Deri A，Tevan G，Sem lyen A，et al．The complex groundreturn plane-asimplifiedmodel forhomogeneousandmultilayerearth return[J]．IEEE Transon Power Apparatusand Systems，1981，100（8）：3686-3693．

[5]WiseW H．Effectofground permeability on ground return circuits[J]．Bell System Technical Journal，1931，10（3）：472-484．

[6]Wedepohl L M．Wave propagation in transmission lines over lossy ground：a new complete field solution[J]．Proceedings of the Institution of Electrical Engineers，1978，125（6）：505-510．

[7]Sem lyen A．Ground return parameters of transmission lines，an asymptotic analysis for very high frequencies[J]．IEEE Trans on Power Apparatus and Systems，1981，100（3）：1031-1038．

[8]Galloway R H，ShorrocksW B，Wedepohl LM，etal．Calculation of electrical parameters for short and long polyphase transmission lines[J]．Proceedingsof the Institution of ElectricalEngineers，1964，111（12）：2051-2059.

[9]Dommel H W．Overhead line parameters from handbook formulas and computer programs[J]．IEEE Trans on Power Apparatusand Systems，1985，104（2）：366-372．

[10]Newman JN．Approximations for the Bessel and Struve functions[J]．MathematicsofComputation，1984，43（168）：551-556．

[11]Aarts RM，Janssen A JEM．Approximation of the Struve function H1occurring in impedance calculations[J]．Journal of the Acoustical Society of America，2003，113（5）：2635-2637．

[12]Gradshteyn IS，Ryzhik IM．Table of Integrals，Series and Products[M]．Burlington：Academic Press，2007．

[13]Jeffrey A，Dai H H．Handbook of Mathematical Formulas and Integrals[M]．Burlington：Academic Press，2008．

[14]PressW H，Teukoslsky SA，VetterlingW T，etal．Numerical Recipes：The Art of Scientific Computing[M]．UK：CambridgeUniversity Press，2007．

[15]李杨，李永丽（LiYang，LiYongli）．750 kV及特高压输电线路的暂态电流研究（Research on transientcurrentof 750 kV and UHV transmission line）[J]．电力系统及其自动化学报（Proceedingsof the CSU-EPSA），2006，18（3）：18-23．

[16]葛耀中，徐丙垠，陈平（Ge Yaozhong，Xu Bingyin，Chen Ping）．利用暂态行波测距的研究（Study of fault location based on travelingwaves）[J]．电力系统及其自动化学报（Proceedingsof the CSU-EPSA），1999，11（3）：17-22．

New Calculation Method of Overhead Transm ission Line Distributed Parameters

JIAOYanjun，YU Jiangtao，WANG Zengping
（State Key Lab ofNew Energy Power System（North China Electric Power University），Beijing 102206，China）

A new calculationmethod of overhead transmission line distributed parameterswith ground return is presented.After the introduction and analysisof the Carson formulaand Dubanton equations，itisproposed to simplify the Carson correction termsby function replacement，which is carried out to avoid the calculation difficulty of Carson formula and the large errorsof Dubanton equations，and a new high precisionmethod is put forward to calculate the distributed parameters of overhead transmission line.The error analysis result indicates that the newmethod has the advantage ofplain calculation expression，continuous calculation value andmore precise calculation results.Themethod can be utilized to replace the Dubanton equations in corresponding calculation and analysis，and is valuable for the analysis，simulation and calculation ofpowersystem.

overhead transmission line；distributed parameter；Carson′s formula；Dubanton equations；Carson′scorrection terms；function replacement

TM743；TP391

A

1003-8930（2015）04-0055-06

10.3969/j.issn.1003-8930.2015.04.010

焦彦军（1963—），男，博士，教授，研究方向为电力系统继电保护。Email：jiao_yanjun@263.com

2013-03-18；

2013-05-29

于江涛（1973—），男，博士，高级工程师，研究方向为电力系统继电保护。Email：fisherhoper@sohu.com

王增平（1964—），男，博士，教授，博士生导师，研究方向为电力系统自动化、电力系统继电保护及变电站综合自动化等。Email：wangzp1103@sina.com