电网连锁性故障序列的模糊综合评价方法

姚薇薇，李华强，贺强，吴星

（四川大学电气信息学院，智能电网四川省重点实验室，成都610065）

电网连锁性故障序列的模糊综合评价方法

姚薇薇，李华强，贺强，吴星

（四川大学电气信息学院，智能电网四川省重点实验室，成都610065）

为研究电力系统在隐性故障下的故障传播路径，在分析隐性故障发生机理的基础上，提出基于扰动距离、潮流过限、潮流转移率和综合脆弱性4类模糊指标的支路故障综合可能性指标。应用灰色关联理论获取指标影响权重，采用模糊综合评价得到支路故障综合可能性指标，并进行故障排序。该方法能够综合考虑多种故障触发不确定因素，更准确地评估预误动集中支路发生故障的可能性。在IEEE 30节点系统的仿真验证了该方法的有效性和普适性。

隐性故障；模糊映射；灰色关联理论；模糊综合评价；连锁故障

规模化、自动化是现代电力系统的发展趋势，也是维护电力系统安全可靠运行的双刃剑。一方面，具有高度自动化特性的互联大型电网增强了对偶发事故的镇定能力，减少了事故的发生频次；另一方面，电力系统结构日益复杂，继电保护参与程度日益增加，一旦系统故障，继电保护系统的不正确动作将加速电力系统压力累积，导致线路过载加重，甚至引发连锁故障，造成大规模的电力系统灾难性事故。对大停电事故的研究表明，约75%的电力大停电事故正与此有关[1]。当前国内外相关领域的专家将隐性故障作为引发电力系统灾难性事故的一种机理，广泛将其运用于连锁故障和电力灾难事故的研究中。

当前基于电力系统隐性故障的研究主要侧重于两方面。

（1）隐性故障机理的探究与模型改进。文献[2-9]提出隐性故障理论和发生机理，基于现有电力系统继电保护种类给出隐性故障基本模型。文献[10]提出基于马尔可夫方法的隐性故障模型，计算保护拒动、误动概率。文献[11]基于历史数据建立保护行为模型，采用蒙特卡洛抽样方法仿真保护动作特性。

（2）基于隐性故障模型计算连锁故障概率或搜索系统脆弱区域。文献[12-13]以隐性故障模型为连锁性故障的传播机制，采用可信性测度刻画故障发生的可能性；文献[14-16]基于继电保护隐性故障模型与风险指标辨识电网连锁故障序列。

部分研究以单一隐性故障模型为基础评估故障发生概率，难以对下级故障做出有效判断。随着连锁故障方向研究深入，综合评价作为更全面的评估手段，逐渐成为研究趋势[13，17-19]。为弥补单一隐性故障模型预测下级故障准确性的不足，本文提出一种模糊综合评价方法。将系统运行参数考虑在内，结合历史统计数据，提出线路故障的综合可能性系数指标，对线路下级故障做出合理选择。通过在IEEE30节点系统的仿真，验证了该方法的合理性。

1 电力系统隐性故障

1.1 隐性故障机理

广义的隐性故障是指所有在正常状态下隐匿，在承压状态偶然暴露的故障。在电力系统领域，隐性故障专指继电保护系统具有隐匿性、范围性、危害性的各类问题。这类问题均在电力系统正常运行时难以排查且对系统暂无影响，一旦系统异常，就会在相应范围对电力系统产生危害。

从继电保护隐患原因上分析，导致继电保护隐患的原因分为两类[2]：一是保护定值不合理，包括定值错误和因为运行方式改变或系统传输能力上升造成保护整定值的过时；二是保护系统本身存在硬件缺陷，包括继电保护装置所处位置的长期负载率、承压等级等环境不同，影响保护系统的硬件绝缘、老化等问题。

1.2 隐性故障模型

现有研究提出了三段距离保护、阶段式电流保护、潮流越限保护3种输电线路的继电保护隐性故障模型[3-8]，其中考虑线路潮流越限的继电保护隐性故障概率模型[9]如图1所示。

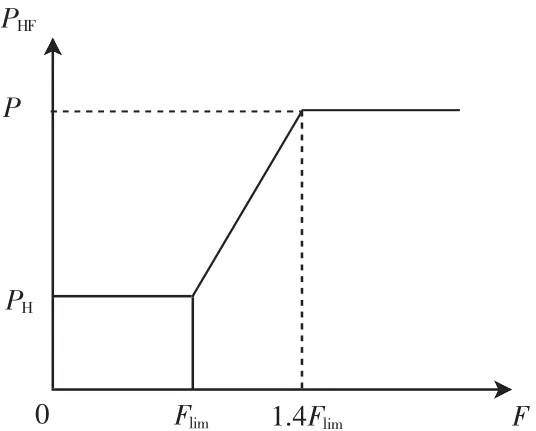
图1 线路潮流越限时保护的隐性故障特性Fig.1 Hidden failure characteristicsof line protection w ith over-flow

图中，PHF表示线路潮流越限隐性故障率，其大小与线路潮流大小相关；P表示继电保护正确动作的概率；PH表示隐性故障统计概率，是根据二次设备条件和自然因素等非一次系统数据分析而来；Fi表示线路i的有功潮流；Flim表示线路的潮流限值。考虑线路潮流越限的隐形故障概率为

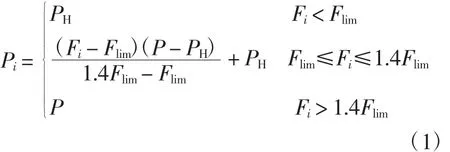
本文正是根据此种模型建立起适应当前系统运行方式下的线路故障综合可能性指标。

2 线路故障综合可能性指标

2.1 综合可能性指标

由考虑线路潮流越限的隐形故障模型可知，当线路潮流不超过潮流限值时，所有线路触发隐性故障的概率一致。但从继电保护隐患原因上分析，电力系统的固有属性和运行状态均影响隐性故障触发的可能性。故严格意义上，不同线路对扰动的承受度与敏感度不同。因而提出线路L故障的综合可能性评价指标PL为

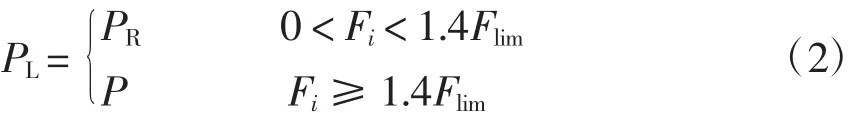
式中，PR为综合可能性评价结果，由模糊综合评价方法计算。当线路潮流过限140%，认为保护正确动作，下级故障可能性就是保护正确动作概率；当线路潮流未过限140%时，则对线路做综合判断，计算下级故障可能性。综合评价因素从隐性故障隐患原因上分析，提取支路的扰动距离、支路潮流、潮流变化率、支路综合脆弱性指标，分别从电网的结构与状态两部分评估引起隐性故障的可能性。

2.2 综合评价因素

2.2.1 扰动距离指标

扰动距离定义为被评价支路到故障支路的距离，用同心松弛理论可以阐释，如图2所示。

根据同心松弛理论，各母线层所受到的扰动影响将随着与故障中心电气距离的增大而逐步衰减。现以故障支路A为圆心，将所有与支路A直接相连的支路设为支路层1，与支路层为1的支路直接相连的支路设为支路层2，以此类推，如图2所示。将每条支路所处的支路层作为当前支路到故障支路的扰动距离。

由于隐性故障的发生具有范围性，存在“准误动集”或“预故障集”。国内外统计资料表明，当一条线路被切除后，与该线路相连的线路或发电机的继电保护装置误动的概率将大大提高[14]。只考虑单重隐性故障的情况，即线路断开只会造成与它两端相连的所有线路中的某一条故障[15]。本文设定支路层不大于2的所有支路为下级故障的预故障集，支路层大于3的线路可认为受扰很小，可忽略不计。

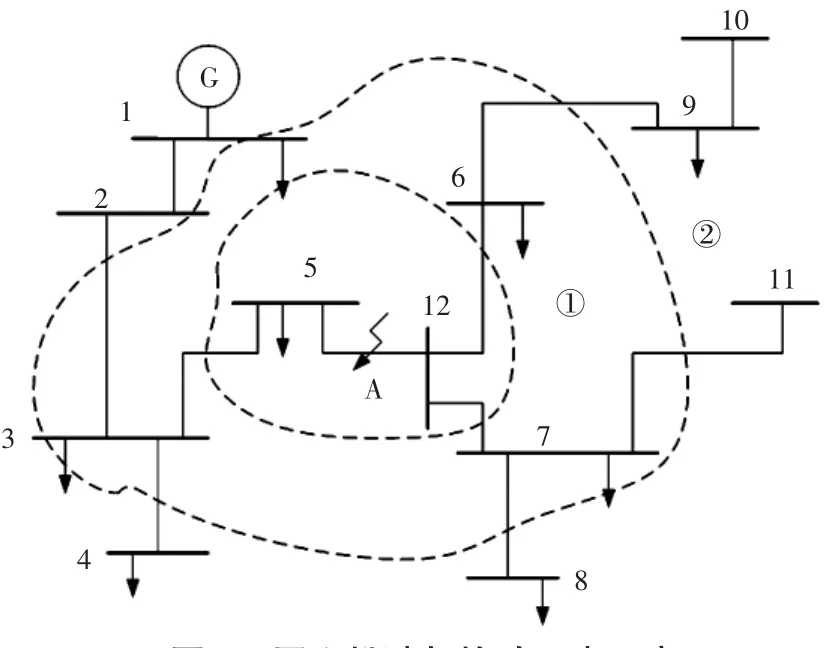
图2 同心松弛与扰动距离示意Fig.2 Relationship between concentric relaxation and disturbance distance

线路断开单因素“扰动距离指标”在评语集上的映射为

式中：V为隐性故障预误动集；da为测试系统的最大层数；db为以当前故障为圆心到电网的最大层数；dis（j）为第j条线路到故障线路的层数；τ1j为支路j到故障线路的扰动距离在评语集上的映射，即对预误动集中支路发生故障可能性的支持程度。

2.2.2 支路潮流过限指标

支路潮流过限指标取原始潮流过限隐性故障模型，表达线路本身存在固有隐性故障风险，故障概率随线路潮流过限程度增加而上升。

单因素“支路潮流过限指标”在评语集上的映射为

式中：j为隐性故障预误动集内所有支路，j∈V；τ2j为支路j潮流越限程度在评语集上的映射，是对预误动集中支路发生故障可能性的支持程度。

2.2.3 支路潮流转移率指标

潮流转移率取当前所发生故障距上一阶段所发生故障在支路潮流变动上的量化值与线路潮流裕度的比值。支路潮流转移率越大，继电器发生误动的可能性一定程度上越大，线路故障的可能性越大。故将其作为评价因素之一纳入考虑。

单因素“支路潮流转移率指标”在评语集上的映射为

式中：nowflowj为当前潮流；bassflowj是上级故障后线路潮流；τ3j为支路j潮流转移率在评语集上的映射，表达当前潮流与上级故障后潮流的转移率对故障预误动集中支路发生故障可能性的支持程度。这里的潮流功率采用线路复功率，因为无功变化剧烈同样可能引起保护误动[20]。

2.2.4 支路综合脆弱性指标

支路脆弱性是支路在正常运行情况或各种随机因素作用下，系统承受干扰或故障能力不断弱化的特性，从属性上剖分为结构脆弱性与状态脆弱性两方面[22]。结构脆弱性属于系统的固有属性，表达各支路稳态潮流长期分配状态。状态脆弱性表达的是系统当前状态距离临界状态的距离，通过系统状态变量构建指标来反映系统当前运行状态的脆弱程度。支路综合脆弱性指标由结构指标和状态指标联合建立，具体算法见文献[20-21]。

支路综合脆弱性指标E（j）为

单因素“支路综合脆弱性”评价集上的映射为

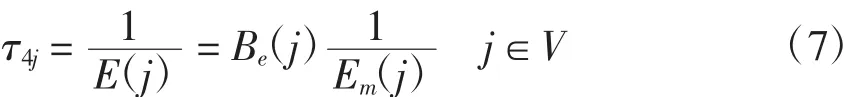
式中，τ4j为支路j综合脆弱性在评语集上的映射。

3 模糊综合评价

模糊综合评价是基于模糊理论的综合评估方法。其基本思想是运用模糊变换原理和最大隶属度原则，根据参评事物的多类评价因素的相互联系做出综合判断。综合评价有3要素：①因素集；②评语集；③单因素判断。

3.1 因素集

因素集U={u1，u2，u3，…，un}，即被评判对象的参评因素集。根据本文的线路故障综合可能性指标，因素集取为：

u1=支路扰动距离指标；

u2=支路潮流过限指标；

u3=支路潮流转移率指标；

u4=支路综合脆弱性指标。

3.2 评语集

评语集V={v1，v2，v3，…，vn}，即可能出现的评判内容。由于所需评判内容为下级故障发生支路，故将评语集取为隐性故障预误动集，m为隐性故障范围内支路总数。本文中选取V为距离故障支路为支路层数不大于2的所有支路。

3.3 单因素判断

单因素判断：即对单因素ui（i=1，2，…，n）逐一评判，得到V上的F集（ri1，ri2，ri3，…，rim），即从U到V的一个模糊映射。

因素集包含4类单因素，为得到各因素在评语集上模糊映射，现建立隶属度函数将4类指标进行模糊化处理

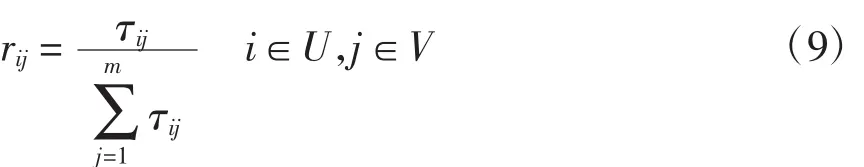
式中：rij表示单因素ui在评语vj上的映射τij对评选内容为j的隶属程度，rij∈（0，1）。于是因素集的每一个成员在评语集上的映射组成评价矩阵R为

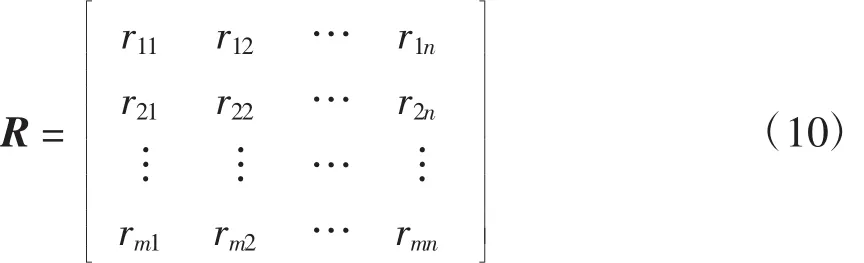
由于各因素地位不一定相等，对最后的判断的参考价值也不等，所以需对各因素加权。本文基于灰色关联理论求取权重矩阵。

3.4 评判权重

灰色关联指的是在不同序列之间由于异同关系不明而导致的序列联系紧密与否不明确的状态。灰色关联度则是这个不明确状态的量化值，是两个序列间的联系度。根据灰色关联理论，若序列所表达的对象发展变化态势越一致，关联度越大；反之关联度越小。运用于本文单因素权重的求取，若单因素序列相互间的关联度越大，两序列的发展态势越趋于一致，其综合评价结果趋同程度就越高，反应客观规律发展的准确度将越高，对应指标的影响权重越大。于是计算单因素间关联度为

式中：i、j为因素集中任意两单因素在评价集上的评价序列；|rih-rjh|为两序列对应元素差；mij为序列对应元素差中最小值；Mij为序列对应元素差中最大值，e为常数，一般e<0.5。

由序列间关联度得到单因素权重为

式中，A为所有与单因素i相关的序列。

于是权重矩阵W为

3.5 综合评判

综合评判一般有两种评判模型：①合成模型：采用模糊算子∧和∨对评价矩阵和权重矩阵进行合成运算；②加乘模型：采用实数的加乘运算，即对评判矩阵和权重矩阵采取矩阵乘的方式运算，运算结果比合成模型更精细。本文采用加乘模型进行综合评判，即

4 算例仿真与分析

4.1 计算步骤

步骤1计算初始故障前系统的稳态潮流和临界潮流，由式（6）计算故障前支路的综合脆弱度；

步骤2由故障前支路综合脆弱度筛选出前15条最脆弱支路作为初始故障集；

步骤3初始故障发生，计算故障后潮流和故障临界潮流；

步骤4判断是否有支路潮流满足Fi≥1.4Flim，若有支路满足，则认为该支路保护正确动作，转至步骤6，若无支路满足转至步骤5；

步骤5由式（3）、（4）、（5）、（7）、（9）计算综合评判指标，对处于误动范围的支路进行综合评判，得到支路误动可能性最大支路作为下级故障；

步骤6判断是否达到搜索深度，如果没有，计算当前故障下系统潮流和临界潮流，跳转到步骤5；如果达到搜索深度或系统电源、负荷孤立，结束。

4.2 算例分析

取线路潮流极限为200MW，不考虑线路保护拒动，即认为P+PH=1。根据2009年全国继电保护装置运行情况统计数据[23]和系统电压等级取P= 0.999 6，PH=1-0.999 6=0.000 4。

4.2.1 初始故障集

稳态潮流下IEEE30节点系统支路的综合脆弱性指标如图3所示。

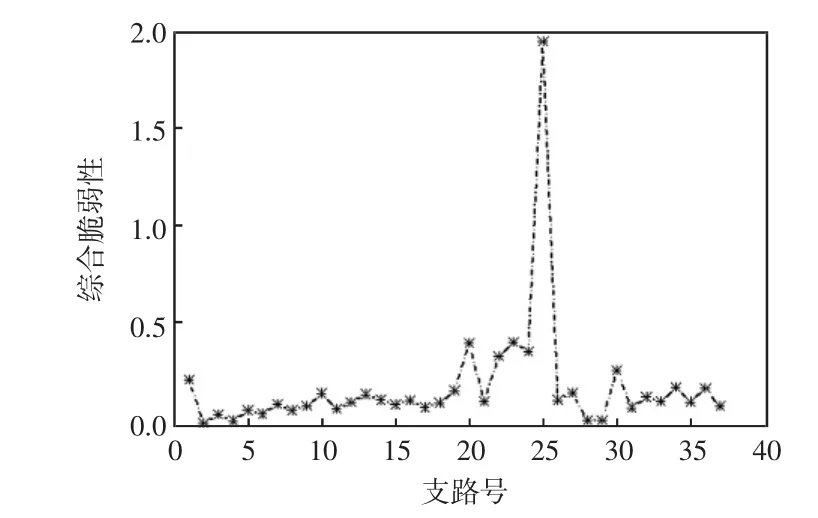
图3 初始故障前系统各支路的综合脆弱性指标Fig.3 Comprehensive vulnerability index of each branch before the initial failure

其中，由综合脆弱性指标具体含义可知，指标数值越小，对应综合脆弱性越大，故从图中选择综合脆弱性指标数值最小的15条支路作为初始故障进行算例分析。

4.2.2 连锁故障序列

取最大序列搜索深度为4，初始故障按照支路综合脆弱性指标排序，评估结果见表1。

表1 连锁故障预测及故障序列指标Tab.1 Forecasting of cascading failuresand involved indicators

表1中SG、SL、SC分别表示发生失电源事故、失负荷事故和低压减载失负荷。以脆弱性最高的2号支路（1，3）作为初始故障进行合理性分析。分析评价矩阵可知，初始故障后，支路L1潮流过限指标值为0.964，潮流过限较严重；支路L1潮流转移量指标同样很高，为0.284，这与L1、L2均与1号发电机相连有关，当L2开断，大量潮流将转移至L1；同时L1与初始故障L2通过节点1直接相连，相隔支路层数为1，发生隐性故障的可能性理应很大，故选择L1作为下级故障具有合理性。

分析表1中连锁故障序列可知，故障序列往往有一定的发生模式，如1、2号发电机相邻线路故障后会引起L1、L3、L2、L5、L6、L8支路中某几条相继开断继而发电机相邻线路潮流过限达到Fi≥1.4Flim进而发电机退出。上述序列中L3-L1-L6-L8、L1-L3-L6-L8、L6-L1-L3-L8为较固定序列。表5中以L28、L37、L18为初始故障的连锁故障序列由于达到搜索深度而停止搜索。如果继续搜索，L36的开断将引起L1支路过载继而触发L1-L3-L6-L8序列；L1、L3的开断将引起L6过载触发L1-L3-L6-L8序列。此外连接较重负荷节点线路如L28、L29故障容易引发同一节点其他支路相继开断继而负荷节点孤立。

表1中传统方法下的故障序列是根据原有基于线路潮流过限隐性故障概率模型仿真得到。当有多条线路潮流越限，或没有线路潮流越限时采用轮盘赌法选取下级故障。仿真可得，当潮流过限为多种不确定因素的主要矛盾时，传统方法和文章方法筛选的序列一致，如以L3、L6、L5为初始故障时搜索的故障路径；一旦潮流过限因素不是主要矛盾，每次仿真中，传统方法根据轮盘赌法所得序列都可能不同。如以L4为初始故障时，相邻线路L2、L3、L7的故障概率均为保护误动概率PH，每次仿真，下级故障可能出现在L2、L3、L7中任何一条。但实际上3条线路由于拓扑结构和潮流状态不同，对扰动的承受能力不应完全相同。故综合评判方法较之传统方法更优更准确，更具实用性。

以线路潮流限值为因变量，对故障序列发生可能性做横向比较，结果见图4所示。

图4不同潮流限值下的故障序列可能性Fig.4 Possibility of cascading failuresw ith different power lim itation

图4 表明，在其他环境因素和运行状况不变的情况下，线路潮流限值越大，故障序列可能性相对越小，这为电力系统安全控制工作提出了相应改进意见。

5 结语

本文基于潮流过限隐性故障模型，设立了扰动距离、潮流过限、潮流转移率和综合脆弱性4类支路模糊指标，采用模糊综合评判对下级故障支路进行预测，预测结果较原有的考虑单一故障触发原因的模型结果更具有效性。评价结果可为电力系统灾难性事故预防提供参考：首先，综合脆弱性最高支路常属于距发电机较近线路或重负荷线路，其故障后将引起较大规模的潮流转移造成相邻支路相继重载或过载，继而触发连锁故障导致大量失负荷。故可认为综合脆弱性高的支路需作为关键支路加强监督和防护，并在系统异常承压时及时控制，不让关键支路因受扰开断。其次，从隐性故障的机理出发，设计具有整定值自适应性能的继电器，加强关键支路的监督，增加线路潮流限值可有效降低线路发生故障的可能性。

[1]Phadke AG，Thorp JS．Expose hidden failures to prevent cascading outages in power systems[J]．IEEE Computer Applications in Power，1996，9（3）：20-23．

[2]施莉，赵东成，杨明玉（Shi Li，Zhao Dongcheng，Yang Mingyu）.关于继电保护系统中隐形故障的探讨（Discussion on hidden failures in relay protection ofpowersystems）[J].继电器（Relay），2004，32（5）：66-69.

[3]Elizondo DC，de La Ree J，Phadke AG，etal．Hidden failures in protection systems and their impact on wide-area disturbances[C]//IEEE Power Engineering Society Winter Meeting.Columbus，USA：2001．

[4]Bae Koeunyi，Thorp James S．An importance sampling application：179 busWSCC system under voltage based hidden failures and relaymisoperations[C]//Hawaii International Conference on System Sciences.Big Island，USA：1998．

[5]Yu Xingbin，Singh Chanan．A practicalapproach for integrated power system vulnerability analysiswith protection failures[J]．IEEE Trans on Power Systems，2004，19（4）：1811-1820．

[6]Bae K，Thorp JS．Stochastic study of hidden failures in powersystemprotection[J]．Decision SupportSystems，1999，24（3/4）：259-268．

[7]王明俊（Wang Mingjun）.大电网继电自动装置的隐藏故障、脆弱性和适应性问题（Hidden failure，vulnerability and adaptability of relaying automations in large interconnected power systems）[J]．电力自动化设备（Electric Power Automation Equipment），2005，25（3）：1-5．

[8]MotterAE，Ying-Cheng Lai．Cascadebasedattackson complex networks[J]．PhysicalReview E，2002，66（6）：1-4．

[9]杨明玉，田浩，姚万业（Yang Mingyu，Tian Hao，Yao Wanye）.基于继电保护隐性故障的电力系统连锁故障分析（Analysisofpower system cascading failurebased on hidden failures of protective relaying）[J].电力系统保护与控制（Power System Protection and Control），2010，38（9）：1-5.

[10]吴旭，张建华，吴林伟，等（Wu Xu，Zhang Jianhua，Wu Linwei，etal）．输电系统连锁故障的运行风险评估算法（Method of operational risk assessment on transmission system cascading failure）[J]．中国电机工程学报（Proceedingsof the CSEE），2012，32（34）：74-82．

[11]李生虎，丁明，王敏，等（Li Shenghu，Ding Ming，Wang Min，etal）．考虑故障不确定性和保护动作性能的电网连锁故障模式搜索（Search of power system chained failuremode considering uncertainty of element fault and performance of protective relaying）[J]．电网技术（Power System Technology），2004，28（13）：27-31，44.

[12]马超，肖先勇，袁志坚，等（Ma Chao，Xiao Xianyong，Yuan Zhijian，etal）．电网连锁性故障发生可能性的模糊模拟评估方法（A fuzzy simulation assessmentmethod ofoccurrence possibility of power grid cascading failures）[J]．中国电机工程学报（Proceedings of the CSEE），2012，32（16）：77-84．

[13]崔振，肖先勇，马超，等（Cui Zhen，Xiao Xianyong，Ma Chao，etal）．基于电网剖分与不确定性测度的电网灾难性事件评估（Assessmentmethod of catastrophic accident in power system based on electric network dissection and uncertainmeasure）[J]．电力系统保护与控制（Power System Protection and Control），2011，39（20）：30-37．

[14]陈为化，江全元，曹一家（ChenWeihua，Jiang Quanyuan，Cao Yijia）．考虑继电保护隐性故障的电力系统连锁故障风险评估（Risk assessmentofpower system cascading failure considering hidden failures of protective relaying）[J]．电网技术（Power System Technology），2006，30（13）：14-19，25．

[15]丁理杰，刘美君，曹一家，等（Ding Lijie，Liu Meijun，Cao Yijia，etal）．基于隐性故障模型和风险理论的关键线路辨识（Power system keylines identification based on hidden failuremodel and risk theory）[J]．电力系统自动化（Automation of Electric Power Systems），2007，31（6）：1-5，22．

[16]张国华，张建华，杨志栋，等（Zhang Guohua，Zhang Jianhua，Yang Zhidong，etal）．电力系统N-K故障的风险评估方法（Risk assessmentmethod ofpowersystem N-K contingencies）[J]．电网技术（Power System Technology），2009，33（5）：17-21，27．

[17]邓慧琼，艾欣，张东英，等（Deng Huiqiong，AiXin，Zhang Dongying，etal）．基于不确定多属性决策理论的电网连锁故障模式搜索方法（Search technique forpowersystem cascading outages based on uncertain multiple attribute decision-making）[J]．电网技术（Power System Technology），2005，29（13）：50-55．

[18]王涛，王兴武，顾雪平，等（Wang Tao，Wang Xingwu，Gu Xueping，etal）.基于概率及结构重要度的电力系统事故链模型与仿真（Power system fault chainmodel and simulation based on probability and structural importance）[J]．电力自动化设备（Electric Power Automation Equipment），2013，33（7）：51-56.

[19]许小兵，吴锡斌，徐培栋（Xu Xiaobing，Wu Xibin，Xu Peidong）.考虑线路停运率的电网连锁故障风险评估（R isk assessment of cascading failure in power grid considering line outage rate）[J].电力建设（Electric Power Construction），2013，34（8）：116-120.

[20]余晓丹，贾宏杰，陈建华（Yu Xiaodan，Jia Hongjie，Chen Jianhua）．电力系统连锁故障预测初探（A preliminary research on power system cascading contingency forecasting）[J]．电网技术（Power System Technology），2006，30（13）：20-25．

[21]陈卓，李华强，周柯宇，等（Chen Zhuo，LiHuaqiang，Zhou Keyu，etal）.考虑风电场影响的电力系统支路脆弱性评估（Vulnerable branch assessment of power system consideringwind farm effects）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（2）：37-43.

[22]王伊渺，李华强，肖先勇，等（Wang Yimiao，LiHuaqiang，Xiao Xianyong，etal）．基于电网状态和结构的连锁故障预测（Cascading failures forecasting based on running state and structure）[J]．电力系统保护与控制（Power System Protection and Control），2012，40（20）：1-5，12.

[23]沈晓凡，舒治淮，刘宇，等（Shen Xiaofan，Shu Zhihuai，Liu Yu，etal）.2009年国家电网公司继电保护装置运行统计与分析（Statistics and analysison operation situation ofprotective relayingsofstate grid corporation of China in 2009）[J]．电网技术（Power System Technology），2011，35（2）：189-193．

Fuzzy Synthetic Evaluation Method of Cascading Failure Sequence in Power Grid

YAOWeiwei，LIHuaqiang，HEQiang，WU Xing
（IntelligentElectric PowerGrid Key Laboratory of Sichuan Province，Schoolof Electrical Engineering and Information，Sichuan University，Chengdu 610065，China）

In order to study the failure propagation path，a comprehensive probability index ofbranch isproposed considering occurrencemechanism of hidden failure in terms of disturbance distance，power exceeding，power transition rate and comprehensive vulnerability-the four fuzzy branch indicators.The grey correlation theory isadpted to approach the impactweights.And afterward the comprehensive branch probability index is calculated applying fuzzy synthetic evaluation，so that the failure sequence is obtained.Taking a variety of fault trigger factors under uncertainty into account to assess the full-scale resultsbased on fuzzy theory，thismethod can sort the failure possibility ofbranches in incorrect tripping set relativelymore accurately.The simulation analysis on the IEEE 30 bus test systemproved out the validity and generaladaptability of thismethod.

hidden failures；fuzzymapping；grey correlation theory；fuzzy synthetic evaluation；cascading failures

TM712

A

1003-8930（2015）04-0079-07

10.3969/j.issn.1003-8930.2015.04.014

姚薇薇（1989—），女，硕士研究生，研究方向为电压稳定及优化问题。Email：925134833@qq.com

2014-04-24；

2014-11-13

李华强（1965—），男，博士，教授，研究方向为电压稳定及优化问题电网稳定与控制研究。Email：lihq1986@hotmail.com贺强（1989—），男，硕士研究生，研究方向为电压稳定及优化问题。Email：279874450@qq.com