基于IPSO优化发电调度的静态电压稳定分析

伍利，陈少芳，南海鹏

（西安理工大学水利水电学院，西安710048）

基于IPSO优化发电调度的静态电压稳定分析

伍利，陈少芳，南海鹏

（西安理工大学水利水电学院，西安710048）

发电机出力增长方式对静态电压稳定临界点有一定的影响，优化发电机有功出力是提高系统静态电压稳定的主要控制手段。文中对粒子群算法中惯性权重和加速常数进行改进，提出以发电增量作为连续潮流的控制变量，实现负荷增量在发电机间的最优分配。该方法以系统静态电压稳定下的最大负载为目标，基于改进粒子群算法优化发电机有功出力，以连续潮流法计算IPSO的适应度函数，确定发电机最优调度模式下的系统最大静态电压稳定裕度。应用该法对IEEE30系统的评估，验证了该方法的正确性和有效性。

静态电压稳定裕度；发电调度；连续潮流法；改进粒子群优化

由于对电力传输容量的巨大需求，考虑追求经济效益和对环境影响的约束，输电系统越来越紧凑，电力设备运行于极限状态，因此电压稳定就成为电力系统安全性和可靠性最大威胁。为了满足经济发展对负荷的要求，电网运行管理部门正在最大限度地挖掘现有输电系统的输电能力。为了充分利用现有输配电系统，系统输电应尽可能地优化配置系统资源并调度系统内设备的运行工况以满足系统的最大需求。在开放的输电环境下，作为提高系统稳定裕度的最经济有效的手段，发电机有功出力调度占有重要地位，因此提高系统静态安全的发电机调度的研究受到广泛关注[1-2]。

目前计算静态电压稳定裕度的主要方法之一有连续潮流法。连续潮流法通过沿PV曲线按一定的步长逐步搜索崩溃点[3-4]，既可以得到负荷节点的PV曲线，还能较好地解决潮流方程在极限点（鞍结分岔点）附近的病态，较好地考虑电力系统的一些约束条件，可靠地跟踪系统稳态运行随负荷的变化情况，得到静态稳定裕度。在此方法中，通常都是基于预先设定的发电机出力增长方式求取电压稳定裕度，这不符合实际系统运行情况。在实际系统中，当负荷水平变化时，各发电机的出力模式可通过不同的调度方式进行调整。按固定的模式调整发电机出力，所得出的计算结果过于保守，从而限制了电能的输送，造成现有资源的浪费[2，5]。因此，如何优化发电调度寻找最大负荷裕度具有一定的实际意义。

电力系统的安全运行需要合理的规划和适当的控制方法来避免电压崩溃，而发电调度对静态电压稳定裕度有较大的影响，利用改进粒子群优化IPSO（improved particle swarm optimization）算法对控制变量进行优化组合可求出系统的最大静态电压稳定裕度MLM（maximum loadingmargin），从而得到提高静态电压稳定裕度的控制措施。本文将IPSO算法引入连续潮流计算中，通过IPSO对发电机出力合理的优化调整，搜寻系统的最大静态电压稳定裕度。此方法通过寻找最优发电状态获得MLM，充分利用已有的发电和输电设备，提高了系统的负荷裕度，求出的电压稳定极限更符合实际。本文还对IPSO的参数进行了改进，加强了它的全局寻优能力，快速且准确地获得更好的优化结果。

1 基本数学模型

从系统给定运行状态出发，按照某种模式，通过负荷或传输功率的增长逐步逼近电压崩溃点。系统当前运行点到电压崩溃点的距离可定义为静态电压稳定裕度。本文选用发电机的有功出力增量作为系统的控制变量，优化的目的是在满足系统运行约束的条件下，通过优化调整控制变量，使系统静态电压稳定裕度达到最大[6-9]。

因此，优化模型的目标函数为静态电压稳定裕度最大，即

为计算方便，取λ0=0。因此目标函数可写为maxλcr。

需满足：

式中：λ0为初始负荷水平；当功率增长到系统鞍结分岔点时，λcr为最大的负荷水平；x为系统状态变量；向量u为控制变量，u=[ΔPG1…ΔPGi…]表示系统内可以参与调度的发电机的有功出力增量，该向量可以包括系统内所有的发电机，也可以根据需要设定可供调节的发电机。不等式约束（3）反映各设备参数如母线电压、发电机的有功和无功出力等的允许范围。式（2）可详细表示[12-13]为

式中：PGi0、QGi0为节点i的初始发电机功率；PLi0、QLi0为节点i的初始负荷功率；Pi为计算出来的节点i的有功功率；Qi为计算出来的节点i的无功功率；ΔPGi为节点i发电机的有功出力增量。

负荷节点的P、Q保持与初始工作点的功率因数不变，故负荷增长可以表示成（1+λ）PLi0和（1+ λ）QLi0。

主要计算过程包括以下两部分。

（1）对粒子群算法进行改进，用改进的粒子群算法优化参与调度的发电机，确定以最大负载能力为目标的发电机的发电状况。在此过程中，以CPF计算IPSO中粒子适应度值。

（2）一旦确定了参与调度的发电机的出力增量，就可以确定各个发电机响应负荷增长的方向GD（generation direction）。可表示为

2 连续潮流法

连续潮流法是电压稳定性分析的有力工具。它可克服接近稳定极限运行状态时的收敛问题[11-12]。连续潮流法由4个基本元素组成：预测、校正、参数化和步长控制。如图1所示，预测步从已知的解（A）开始，以一个切线预报来估计对于一个规定负荷增长方式的解（B）；然后校正步，利用常规潮流求出准确解（C）；负荷进一步增加时，根据新的切线预报电压值。如果新的估计负荷超出了准确解的最大负荷，则以节点电压为固定值进行校正计算来求准确解（E）；当接近电压稳定极限时，为确定准确的最大负荷，在连续预报中，负荷的增量应逐步减少。

目前，制约CPF计算效率的关键有两点：一是解潮流方程时每次迭代都需要形成雅可比矩阵，计算量大，占用内存多，速度慢；二是步长控制，选取小步长，可以得到比较精确的稳定极限，但计算很耗时；选取大步长，计算出的电压稳定极限不够精确，甚至可能导致解的不收敛。本文采用基于PQ分解法的局部参数CPF；参考文献[13]，在预测和变步长时使用牛顿二次插值技术来有效地控制步长的方法，以解决步长控制困难问题。牛顿插值的主要思想在文献[13]有具体的描述。

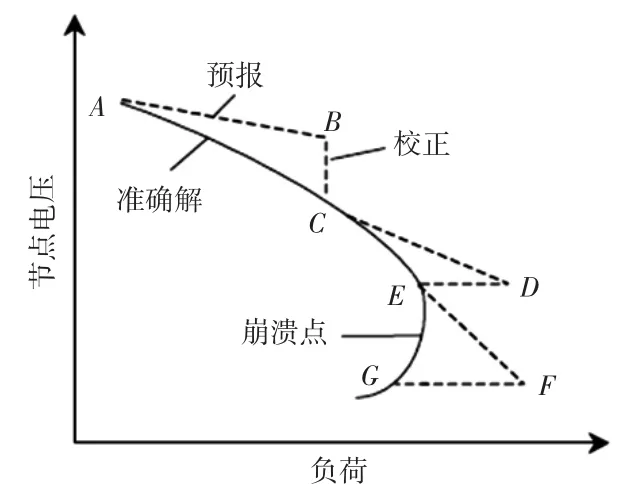
图1 连续潮流的预测与校正Fig.1 Prediction and correction of CPF

3 改进粒子群算法

为了把损耗包括在每个发电机增量里，式（11）应变为

粒子群算法（PSO）是人们受到社会体系中个体行为的启示而提出的一种优化算法，它通过群体的信息共享与个体自身经验的总结来修正个体行动策略，最终求取优化问题的解。

PSO算法先生成初始种群，即在解空间中随机初始化一群粒子，粒子的位置表示待优化问题的解，解的优劣程度由目标函数确定的适应值决定。每个粒子将在解空间中运动，并由一个速度决定其飞行方向和速率大小，然后通过逐代搜索找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个极值就是粒子本身所找到的最优解，这个极值称为个体极值pbest。另一个极值是整个种群目前找到的最优解，这个极值是全局极值gbest。每个粒子更新自己的速度和在解空间的位置[14-16]的公式为

在PSO中，粒子在搜索空间的位置对应于参与调度的发电机有功增量（控制变量），每个粒子的搜索空间（维数）为控制变量个数。粒子xi为

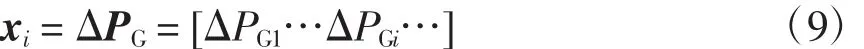
参与调度的发电机增量ΔPG根据电力系统稳定运行的要求应该满足一定的约束条件[12]，即

式中：i为参与调度的发电机数；μ为参与负荷增长

式中：wmax为搜索开始时最大的惯性权重；wmin为搜索结束时最小的惯性权重；k和kmax分别表示当代迭代次数和最大迭代次数。

2）加速常数的改进

对c1、c2合适的取值可以加快算法的收敛速度，减少陷入局部最优的可能性。如果c1=0，此时粒子没有认知能力，收敛速度较快，但更易于陷入局部最优。如果c2=0，此时粒子间没有信息共享，能成功得到全局最优解的概率非常低。为此，调整加速常数的公式为

式中：c1e、c2e分别为c1、c2的终值；c1s、c2s分别为c1、c2的初始值。本文根据文献[16]研究，当c1由2.15线性递减至0.15，c2由0.15线性递增至2.15时，算法能获得最优的适应值。

3.2 基于IPSO的CPF静态电压分析步骤

步骤1输入原始数据及所需参数。设置IPSO算法的运行参数，输入所有相关电气数据。

步骤2初始化。以式（2）中的控制变量u作为IPSO中的粒子。在m维空间按式（16）随机初始化nP个粒子，以保证粒子在控制变量的取值范围之内。

式中：第i个粒子位于xi，速度为vi，m维即参与调度的发电机数，umax、umin为控制变量u的上下限。

步骤3适应值的选取及计算。将目标函数（1）作为适度值，即

对每个个体对应的系统的初始状态进行连续潮流计算，按式（17）计算该个体的适应度值，即静的节点数；η为网络损耗因子，需根据不同的系统而定。

3.1 针对标准粒子群算法的改进

1）惯性权重的改进

惯性权重系数w的合理选择能有效地调整粒子的全局和局部搜索能力的平衡。在开始搜索时，将设置成较大的值以推动粒子在搜索空间进行全局搜索以提高搜索效率，而在搜索后期，w随时间线性递减以保证粒子能够在极点周围做精细地搜索。w的修正公式[15]可表示为态电压稳定裕度。

步骤4按照方程（13）~方程（15）对粒子的惯性权重和加速常数进行更新。

步骤5粒子的状态更新。用式（7）和式（8）对每一个粒子的速度和位置进行更新。如果vi＞vmax将其设置为vmax，如果vi＜vmin将其设置为vmin。

步骤6评估每个粒子的适应值，更新pbest和gbest。对每个个体对应的系统初始状态进行连续潮流计算，计算该个体的适应度即λcr。如果好于该粒子当前的个体极值，则将pi设置为该粒子的位置，且更新个体极值。如果所有粒子中最好的个体极值好于当前的全局极值，则将pbest设置为该粒子的位置，更新全局极值。

步骤7检验是否符合结束条件。如果当前的迭代次数达到了预先设定的最大次数Tmax，则停止迭代，输出最优解，否则转到步骤4。图2为基于IPSO计算静态电压稳定裕度的基本流程。

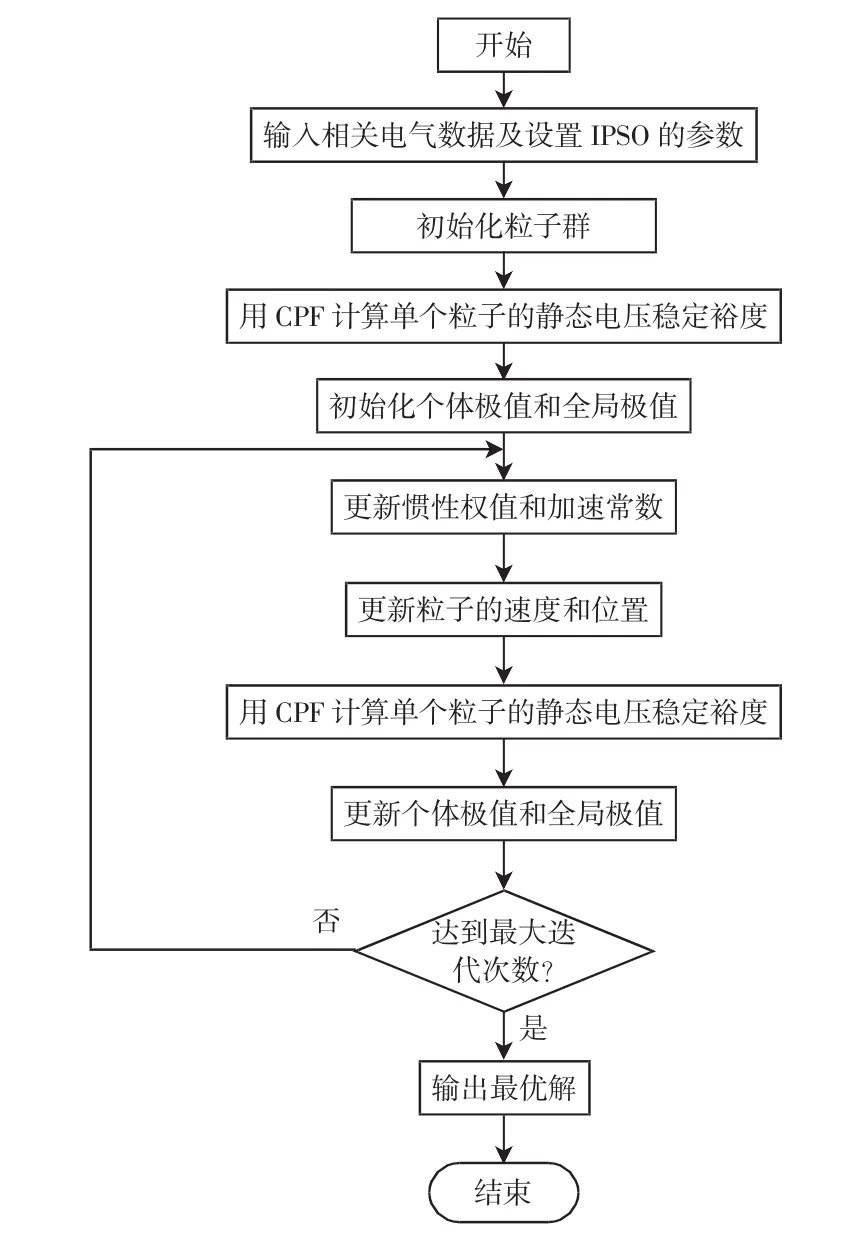
图2 IPSO静态电压稳定裕度的流程Fig.2 Flow chart for calculatingmaximum static voltage stabilitymargin via IPSO

4 算例结果与分析

以本文的方法，对IEEE30节点系统进行仿真分析，系统接线如图3所示。系统优化的控制变量为5个可调发电机的有功出力增量（除去平衡节点）。在静态电压稳定裕度求取的过程中，由于采用的是全网负荷同步增长方式，因此通过计算可得到本文所提的粒子群算法的参数设置为：群体规模为30；最大迭代次数为250，达到最大迭代次数则终止程序的运行，wmax= 0.9，wmin=0.4；c1由2.15线性递减至0.15，c2由0.15线性递增至2.15；为了使目标函数尽快达到最优，本文的粒子群算法对粒子的飞行速度也进行了限制（-0.3≤v≤0.3）。

图3 IEEE 30节点系统Fig.3 IEEE 30-bus system

发电机的出力增长方式目前主要有两种：

（1）根据发电机当前的出力多少增长，即可以表示成PGi=（1+λ）PGi0，即第1种发电机出力方法。

（2）发电机按初始出力的比例来分配增长的负荷功率，即可表示成，即第2种发电机出力方法。

本文将所提的改进粒子群算法与上述所提的两种传统方法进行比较。采用以上3种方法时各控制变量的最优解和最大电压稳定裕度如表1和表2所示（表中各变量为标么值）。

由表1和表2可知，不同的控制变量组合可以得到不同的负荷裕度，通过调整发电机有功出力，可以影响系统的静态电压稳定裕度。与传统连续潮流（法1和法2）相比，本文所提的方法得到的负荷裕度有了一定程度增加，这是因为本文方法能在更大的区域内寻求到控制变量的最佳组合方式，以实现静态电压稳定裕度的最大化。在实际系统中，通过对控制变量的优化调整，使得系统运行于某一状态时具有更大的稳定裕度，对实际系统的运行控制具有更大的指导意义。系统达到最大负荷裕度时参与调度的发电机响应负荷增长的方向由表3所示。

表1 3种情况下的IEEE30节点的控制变量的最优解Tab.1 Optimalsolution of controlvariablesof IEEE30-bus system w ith three cases

表2 系统的静态电压稳定裕度Tab.2 Static voltage stabilitymargin of the benckmarking system

表3 系统获得MLM时发电机响应负荷增长方向Tab.3 Bestgeneration direction w ith MLM

图4为采用IPSO算法时，系统最危险节点优化前后的PV曲线。由图可知，应用IPSO算法能有效提高系统的电压稳定裕度，计算结果较佳。图5为此次验证过程中最易崩溃点及其附近负荷节点的电压变化情况。图6显示了迭代过程中，IPSO最优值随迭代次数增加而变化的情况。由图5可知本文所用的IPSO算法收敛速度快且有较好的收敛效果。

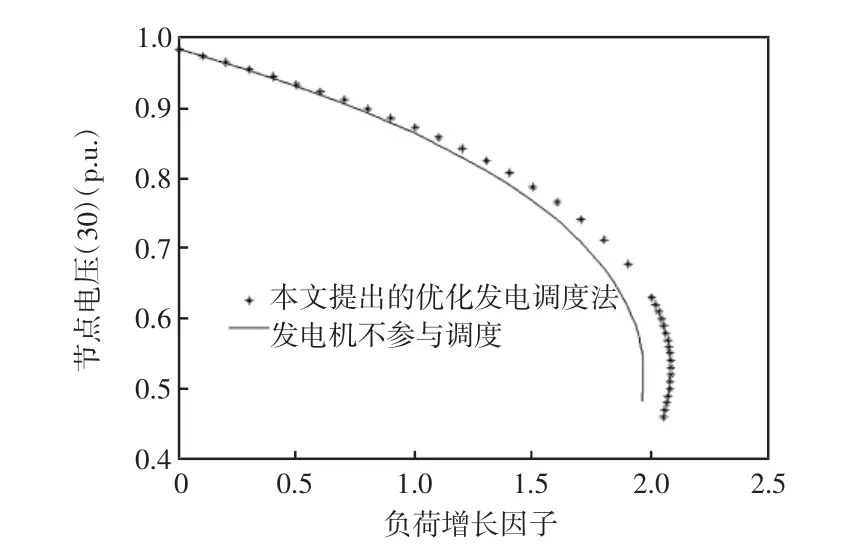
图4 两种情况下最危险节点的P-V曲线Fig.4 Mostendangered nodes′P-V curvew ith two cases

图5 负荷增长时影响最大的节点电压Fig.5 Bus voltage in 14、21、22、27、28 and 30w ith load augmentation

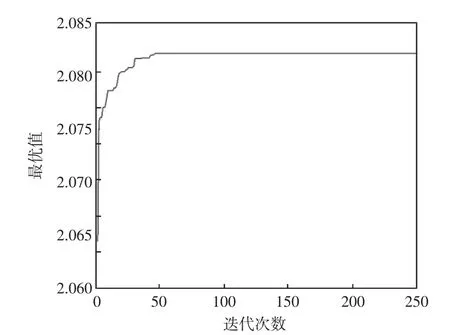
图6 最优值随迭代次数的变化Fig.6 Curve ofoptimalvaluew ith iteration number changes

5 结论

（1）本文针对目前求解系统负荷裕度的方法中缺乏对发电机有功出力优化调度的合理考虑，提出了一种基于IPSO算法优化发电机出力的连续潮流方法，相对于以往的出力方法更好地考虑了发电机之间出力的协调关系。实际系统计算表明，该算法能有效提高系统的负荷裕度，是对常规计算方法的有效改进。

（2）本文方法是充分利用已有的发电和输电设备来提高稳定裕度，求得更有利于指导系统实际运行的最大静态电压裕度，为调度运行人员制定电压稳定控制的具体方案提供了有效的信息。

（3）对IPSO算法的参数进行改进，增强了全局搜索能力，有效摆脱了局部最优解搜索到全局最优解，提高寻优效率。

[1]戴博，张建华，刘军，等（DaiBo，Zhang Jianhua，Liu Jun，etal）.考虑动态电压安全的发电机有功出力最优调整（Active power output rescheduling with dynamic voltage stabilitymargin considered）[J]．电网技术（Power System Technology），2009，33（3）：44-48．

[2]王成山，魏炜，徐德儒，等（Wang Chengshan，WeiWei，Xu Deru，etal）．考虑发电机调度的电力系统输电能力的计算（Calculation ofpower system transmitting capability considering generator dispatch）[J]．电网技术（Power System Technology），2001，25（9）：21-23，27．

[3]蔡伟程，代静（CaiWeicheng，Dai Jing）．对求取电力系统PV曲线的连续潮流法的改进（Improvementof continuation method in tracing PV curves of power systems）[J]．电力系统及其自动化学报（Proceedingsof the CSUEPSA），2005，17（5）：82-85．

[4]赵晋泉，张伯明（Zhao Jinquan，Zhang Boming）．连续潮流及其在电力系统静态稳定分析中的应用（Summarization of continuation power flow and its applications in static stability analysis of power system）[J]．电力系统自动化（Automation of Electric Power Systems），2005，29（11）：91-97．

[5]祝达康，程浩忠（Zhu Dakang，Cheng Haozhong）．求取电力系统PV曲线的改进连续潮流法（An improved continuation method in tracing PV curvesof power systems）[J]．电网技术（Power System Technology），1999，23（4）：37-40，48．

[6]胡彩娥（Hu Cai’e）．应用基于连续潮流算法的遗传算法进行静态电压稳定分析（Application of continuous power flow based genetic algorithm to analysis of static voltage stability）[J]．电网技术（Power System Technology），2004，28（15）：57-61．

[7]李超，陈允平（LiChao，Chen Yunping）．应用基于连续潮流法的改进差异进化算法分析静态电压的稳定裕度（Application of the improved differential evolution calculationmethod based on continuous power flow to the analysis of marginal static voltage stability）[J]．动力工程（Journalof Power Engineering），2006，26（5）：756-760．

[8]李宏仲，金义雄，程浩忠，等（LiHongzhong，Jin Yixiong，Cheng Haozhong，etal）.基于改进粒子群优化算法并计及静态电压稳定性的电力系统无功规划（Reactive power planning based on improved particle swarm optimizationwith static voltage stability）[J]．电网技术（Power System Technology），2005，29（22）：50-55．

[9]蔡智慧，唐忠，马士英，等（Cai Zhihui，Tang Zhong，Ma Shiying，etal）．基于遗传禁忌混合算法的静态电压稳定裕度计算（Static voltage stabilitymargin calculation based on genetic/tabu search hybrid algorithm）[J]．电力科学与技术学报（Journal of Electric Power Science and Technology），2007，22（4）：31-35．

[10]Ya-Chin Chang，Chin-Lien Su．Optimum generation direction for transmission systemmaximum loadingmargin considering static voltage stability[C]//IEEE Power and Energy Society GeneralMeeting.Pittsburgh，USA：2008．

[11]李娟，陈继军，司双，等（Li Juan，Chen Jijun，SiShuang，etal）．连续潮流与免疫遗传算法结合的静态电压稳定裕度计算（Calculation of static voltage stability margin based on continuation power flow and immune genetic algorithm）[J]．电力系统保护与控制（Power System Protection and Control），2010，38（18）：24-27，32．

[12]王锡凡，方万良，杜正春．现代电力系统分析[M]．北京：科学出版社，2003．

[13]伍利，古婷婷，姚李孝（Wu Li，Gu Tingting，Yao Lixiao）．基于改进连续潮流法的静态电压稳定分析（Static voltage stability analysisbased on improved continuation power flow）[J]．电网技术（Power System Technology），2011，35（10）：99-103．

[14]朱童，李小凡，鲁明文（Zhu Tong，Li Xiaofan，Lu Mingwen）．位置加权的改进粒子群算法（Improved particle swarm optimization algorithm with position weighted）[J]．计算机工程与应用（Computer Engineering and Applications），2011，47（5）：4-6，16.

[15]王坤，王蔚，张智晟，等（Wang Kun，Wang Wei，Zhang Zhisheng，etal）．电力系统经济负荷分配的改进粒子群算法（Improved particle swarm optimization algorithm for economic load dispatch of power system）[J]．青岛大学学报：工程技术版（JournalofQingdao University：Engineering&Technology Edition），2009，24（1）：79-84．

[16]李兴源，王秀英（LiXingyuan，Wang Xiuying）．基于静态等值和奇异值分解的快速电压稳定性分析方法（Fast voltage stability analysismethods based on static equivalence and singular value resolution）[J]．中国电机工程学报（Proceedingsof the CSEE），2003，23（4）：1-4，20．

Analysisof Static Voltage Stability Based on Improved Particle Swarm Optim ization to Optim izeGeneration Dispatch

WU Li，CHENShaofang，NANHaipeng
（InstituteofWaterResource and Hydroelectric Engineering，Xi'an University of Technology，Xi'an 710048，China）

Generator active power outputgrowthmode greatly affects the static voltage stability critical point，one of themain controlmeans to enhance power system stability is the optimization of the active poweroutputof the generator. Taking the generation increments as the control variables in the continuation power flow（CPF）to effectively achieve load dispatch among participating generators is proposed，in which the inertiaweightand acceleration coefficients for particle swarm optimization（PSO）algorithm are improved.Themethod treats themaximum loadingmargin under the static voltage stability as the objective function，and adjusts the active poweroutput incrementofeach generator based on improved particle swarm optimization（IPSO）and utilizes CPF to calculate the fitness function of IPSO，ultimately determine themaximum static voltage stabilitymargin under the optimalgenerator schedulingmode.The application of thismethod to IEEE30-bussystems indicates that the proposedmethod is feasibleand effective．

static voltage stabilitymargin；generation dispatch；continuation power flow；improved particle swarm optimization（IPSO）

TM744

A

1003-8930（2015）04-0092-06

10.3969/j.issn.1003-8930.2015.04.016

伍利（1970—），女，博士，讲师，研究方向为电力系统规划与运行。Email：wuli@xaut.edu.cn

2013-02-26；

2013-10-28

陈少芳（1986—），女，硕士研究生，工程师，研究方向为电力系统测量与控制。Email：460218164@.qq.com

南海鹏（1962—），男，博士，教授，研究方向为发电机运行过程控制。Email：hxnhp@163.com