市场环境下考虑电价的机组组合问题比较
2015-07-10熊高峰蔡振华谢上华刘曼
熊高峰,蔡振华,谢上华,刘曼
(湖南大学电气与信息工程学院,长沙410082)
市场环境下考虑电价的机组组合问题比较
熊高峰,蔡振华,谢上华,刘曼
(湖南大学电气与信息工程学院,长沙410082)
为了比较市场环境下基于电价的确定性机组组合问题与考虑电价不确定性的随机机组组合问题模型的优劣,该文定义了两种风险指标,并采用改进粒子群算法求解这两种机组组合问题。在求解过程中,将机组组合问题分解为确定机组开停机表和确定机组出力的两阶段优化问题,并引入最小开停机修复策略。算例表明,在不同风险态度下,发电商应采取不同的机组组合问题数学模型并进行求解和决策。
基于电价的确定性机组组合问题;考虑电价不确定性的随机机组组合问题;风险指标;改进粒子群优化
机组组合问题是电力生产过程中主要问题之一,它是一个高维数、非凸、离散、非线性优化问题。传统的机组组合UC(unit commitment)问题是以系统总发电成本最小为目标。由于带来的经济效益显著,目前针对该问题已提出了多种优化方法,如优先顺序法[1]、动态规划法[2]、拉格朗日松弛法[3]、遗传算法[4]等。在传统机组组合问题中,负荷值一般是事先给定,而在随机机组组合SUC(stochastic unitcommitment)问题[5-7]中,则采用情景分析法对负荷的不确定性进行建模并求解。
在电力市场环境下,机组组合问题的目标函数及约束条件均已发生改变。对发电商而言,市场环境下基于电价的确定性机组组合PBUC(price based unitcommitment)问题是指在一定调度周期内,在满足合同供电要求及机组运行技术要求的条件下,合理确定机组的开停机方案及其出力大小以使发电商利润最大。市场环境下PBUC问题的求解能为发电商提供竞价所需的信息,使发电商在市场竞争中处于有利地位。文献[8-9]对PBUC问题的数学模型和求解算法进行了综述。在建模和求解PBUC问题时,电价一般也作为已知量事先给定,然而由于电价波动性较大且难以精确预测,因此针对电价的不确定性,文献[10-12]建立了考虑电价不确定性的随机机组组合SPBUC(stochastic pricebased unitcommitment)问题的数学模型并进行了求解。
一般而言,未考虑电价不确定性的PBUC问题的求解速度快,而考虑了电价不确定性的SPBUC问题的求解速度较慢,对发电商而言,采用哪种模型较为合适尚未得到很好的结论。
为此,本文采用改进粒子群算法对这两种机组组合问题数学模型求解,在不同工况和风险指标下,对其最优解进行了比较。计算结果表明,在不同风险态度下,发电商应采取不同的机组组合问题数学模型并进行求解和决策。
1 数学模型
1.1 PBUC问题的数学模型
假定机组台数为N,调度周期为T,则PBUC问题的数学模型[8]为
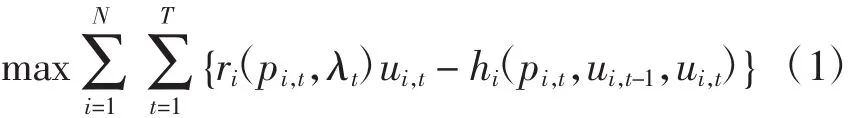
满足以下约束条件:

式中:r(ipi,t,λ)t为第i台机组发电收入,r(ipi,t,λ)t= pi,tλt;h(ipi,t,ui,t-1,ui,)t为第i台机组的发电成本,hi(pi,t,ui,t-1,ui,)t=f(ipi,)t+g(iui,t-1,ui,)t;f(ipi,)t为机组i的运行成本,表示为机组出力的二次函数,f(ipi,)t= ai0+ai1pi,t+ai(2pi,)t2,此处,ai0,ai1,ai2为机组i的运行成本的系数;g(iui,t-1,ui,)t为机组i的启动成本;λt和分别为时刻t的预测电价和预测负荷;pi,t和ui,t分别为机组i在时刻t的输出功率和开停机状态(ui,t=0表示机组停机,ui,t=1表示机组开机)分别为机组i的最小停机和最小开机时间;qi和Qi分别为机组i的最小和最大出力;T分别为机组i在t时刻已连续停机和开机的时间。
PBUC问题的目标函数是最大化发电商的利润。式(2)为机组的功率平衡约束条件,式(3)和式(4)分别为机组的最小开机和最小停机时间约束条件,式(5)为机组出力的上下限约束条件。
1.2 SPBUC问题的数学模型
建立在情景分析基础上的SPBUC问题的数学模型[11]为
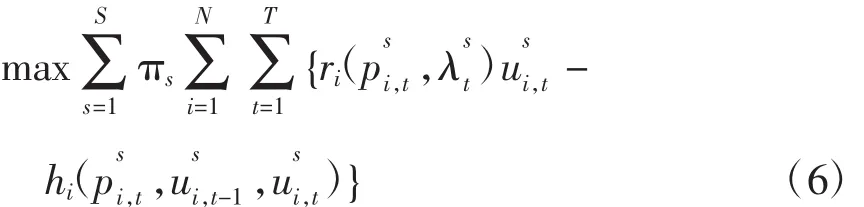
满足以下约束条件:
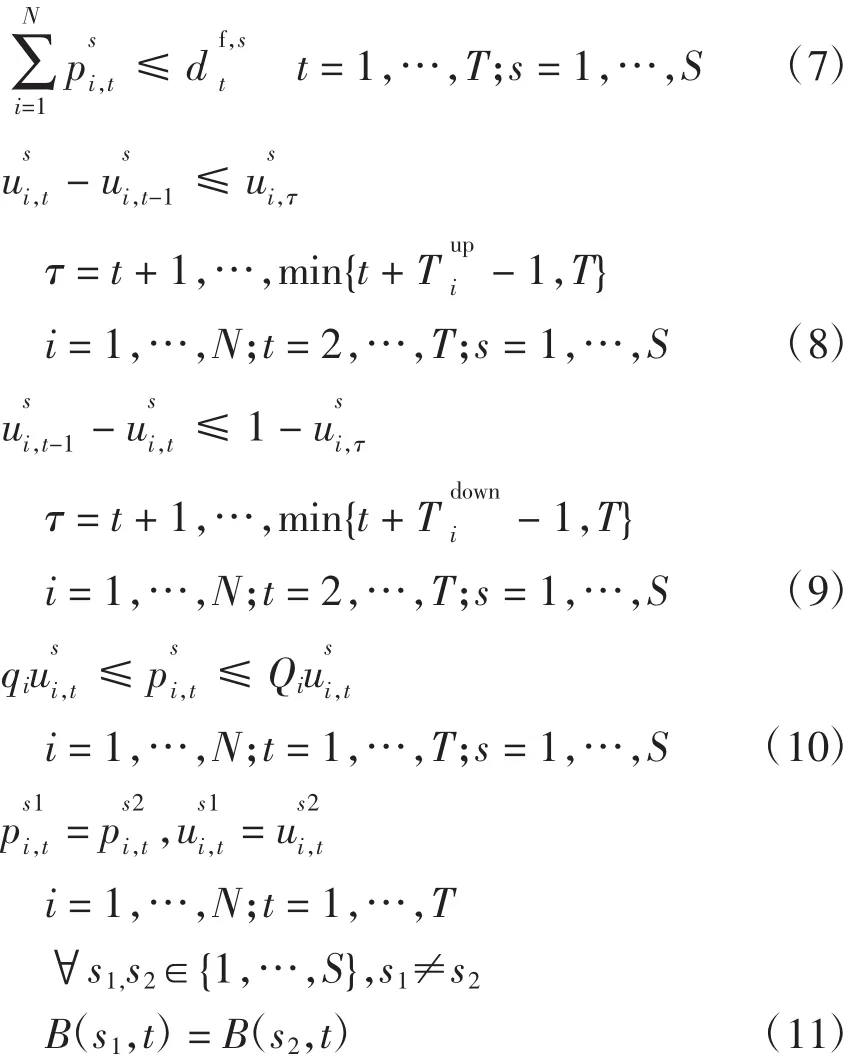
式中:S为电价情景数;πs为情景s发生的概率;分别为情景s下机组i在时刻t的输出功率和开停机状态分别为情景s下时刻t的预测电价和预测负荷。
SPBUC问题的目标函数是最大化所有情景下利润的期望值。式(8)和式(9)分别为情景s下机组的最小开机和最小停机时间约束条件;式(11)为情景簇约束条件。SPBUC问题是一个包含有S个PBUC问题的大规模混合整数非线性规划问题,它是PBUC问题的一个推广。如果只有一个情景,则其就是PBUC问题。
2 风险指标
由于期望下行风险能反映发电商目标利润的损失情况,而波动风险能反映发电商决策方案的收益波动性,故本文采用这两种风险指标来衡量两种机组组合问题模型的优劣。
2.1 期望下行风险
假定发电商的目标利润为ε0,发电商在情景s下获得的利润profits,则发电商在情景s下的下行风险为
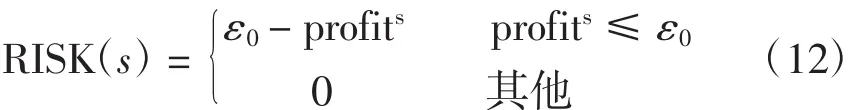
式(12)说明:如果情景利润大于目标利润,则发电商将不会有损失,即下行风险为0;反之,则发电商的下行风险为目标利润与情景利润之差。
为了综合考虑目标利润在各个情景下的风险情况,引入期望下行风险,其定义为

对发电商而言,期望下行风险越小,表示发电商的决策越优。
2.2 波动风险波动风险一般采用标准差来表示,即

式中,E表示决策方案的期望值利润。
波动风险越小,表示发电商收益的波动性越小,故决策方案越优。
3 基于改进粒子群算法的求解
本文采用改进粒子群算法对PBUC和SPBUC问题进行求解。由于SPBUC问题是一个包含有S个PBUC问题的多阶段随机规划问题,求解过程较复杂,因此为简单起见,本文将SPBUC问题简化为两阶段随机规划问题求解,第1阶段求解调度表中各机组的开停机状态变量,并令调度表中开停机变量在所有情景下固定不变,第2阶段则计算此调度表中各机组在各电价情景下的出力,即SPBUC问题的目标函数式可以采用形式为

3.1 粒子群算法的基本原理
粒子群算法[13]是由美国电气学家Eberhart和Kennedy于1995年提出,是一种启发式智能优化算法。粒子群算法的思想最初来源于鸟群(粒子)对食物(最优解)的搜索。该算法中的种群由多个粒子组成,每一个粒子在多维搜索空间中飞行以寻求最优解。在飞行过程中,各个粒子根据自身的经验(粒子目前找到的最优位置)以及同伴的经验(同伴目前找到的最优位置)来调整自身的速度与位置,通过速度与位置的多次调整,粒子群最终能找到最优解。与其他进化算法相比,该算法容易实现且需要调整的参数少。
假定x和v分别表示粒子在搜索空间中的位置和速度,pbest表示粒子目前最优位置,gbest表示种群中所有粒子的目前最优位置,则修正的粒子速度和位置计算公式分别为
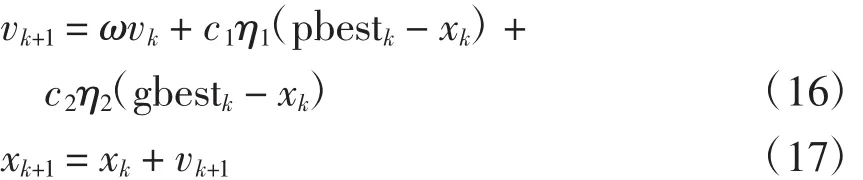
式(16)中,右边第1项为表征粒子对新空间探索能力的动量项;第2项为“认知”部分,表征粒子对自身最优解的学习能力;第3项为“社会”部分,表征粒子间的协作关系。其中,ω为惯性系数,较大的ω表示粒子的全局搜索能力强,较小的ω表示局部搜索能力强;vk和vk+1分别为粒子当前的速度和修正后的速度;c1和c2为加速常数;η1和η2为均匀分布在(0,1)之间的随机数;xk和xk+1为粒子当前位置和修正后位置;pbestk为粒子本身目前搜索到的最优解的位置;gbestk为种群目前搜索到的最优解的位置。
3.2 基于改进粒子群算法求解的具体实施
3.2.1 编码方法
本文采用大小为N×T的二进制矩阵对粒子进行编码,每个编码矩阵表示机组的一个调度表,矩阵中的第i行j列元素表示第i台机组在第j时刻的开停机状态,0表示停机,1表示开机。
3.2.2 粒子的种群初始化
随机初始化一个包含粒子数目为L的初始种群,每个粒子维数为N×T的编码矩阵。
3.2.3 最小开停机时间修复策略
在粒子群进化过程中,本文采用文献[14]中的最小开停机时间修复策略对粒子编码矩阵进行修复,即:若机组的连续开机时间小于其最小开机时间,则该机组将继续开机;若机组的连续停机时间小于其最小停机时间,则该机组将继续停机。
3.2.4 机组出力计算
给定调度时刻t的电价λt,则满足利润最大化的机组i的出力[15]计算式为

3.2.5 适应度函数
采用目标利润作为评价粒子优劣的适应度函数,若某粒子的利润较大,则其对应适应度值较高;反之,其适应度值较低。
3.2.6 算法终止条件
采用给定的最大迭代次数G作为算法的终止条件。
3.2.7 改进粒子群算法的求解步骤
采用改进粒子群算法[16-18]求解PBUC和SPBUC问题的具体步骤如下:
(1)随机产生L个大小为N×T的二进制编码矩阵粒子。
(2)对产生的L个粒子,采用最小开停机时间修复策略对其编码矩阵进行修复。
(3)计算每个粒子的适应度值。对于PBUC问题,适应度值为粒子编码矩阵在给定电价下的利润值;对于SPBUC问题,适应度值为粒子编码矩阵在所有情景下的利润的期望值。
(4)以各粒子的编码矩阵作为该粒子的个体极值pbest,选出所有个体极值中适应度值最大的粒子,并以其编码矩阵作为全局极值gbest。
(5)更新粒子的速度公式为
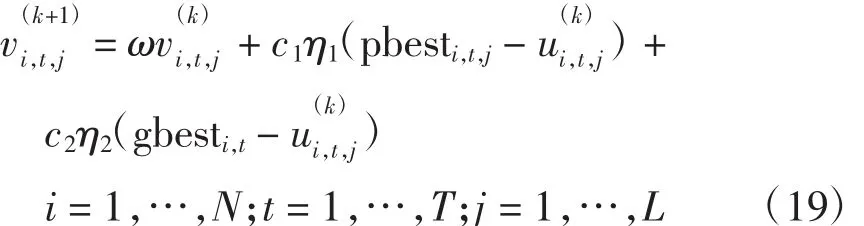
式中,ω=ωmax-(ωmax-ωmin)×g/G,g为迭代次数。

式中:rand()表示(0,1)之间的随机数;S()为模糊转换函数。
(8)采用最小开停机时间修复策略修复新粒子的编码矩阵,计算修复后各个新粒子的适应度值,对各个粒子,若粒子的适应度值优于先前个体极值的适应度值,设置当前粒子的编码矩阵作为个体极值pbest。
(9)选出所有个体极值中适应度值最优的粒子,并以其作为全局极值gbest。
(10)如果达到最大迭代次数,则算法结束。此时,全局极值gbest为所求机组组合问题的最优调度表,其适应度值为所求问题的目标函数值;否则返回步骤(5)。
4 测试结果
采用C语言对本文算法进行编程,并在一个10机组的测试系统上进行测试,调度周期为24 h,各机组相关参数见文献[4]。
为了保证电价数据的真实合理性,对2012年9月美国PJM电力市场的电价数据[19]进行统计分析,以该月每天各小时的期望值电价作为PBUC问题中的预测电价,如表1所示;以各天24 h的电价序列作为情景,由此产生SPBUC问题中的30个电价情景。
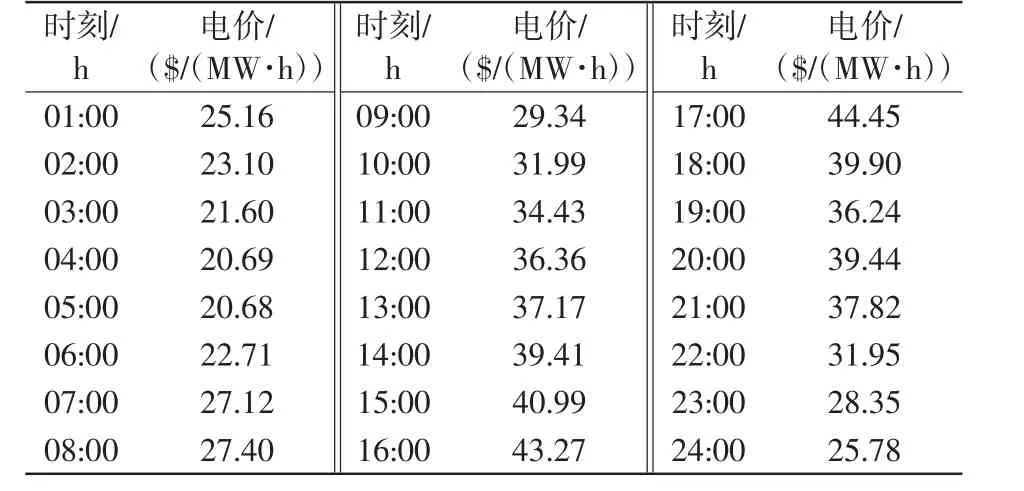
表1 预测电价Tab.1 Forecasted electricity prices
在改进粒子群求解算法中,令G=1 200,种群大小L=40,惯性系数的最大最小值分别为ωmax= 0.9、ωmin=0.4,粒子速度的最大及最小值分别为vmax=300、vmin=-300,加速常数c1=200、c2=200;因改进粒子群算法是一种随机搜索算法,所求得的解不一定每次都是最优解,故在求解各个算例时,分别进行15次独立运算并从中选出最优解。
表2给出了在预测电价下PBUC问题的最优调度表,表3给出了在30个电价情景下SPBUC问题的最优调度表。

表2 PBUC问题的最优调度表Tab.2 Optimalschedule of PBUC problem

表3 SPBUC问题的最优调度表Tab.3 Optimalschedule of SPBUC problem
计算波动风险时,各最优调度表在30个情景下算得的标准差即为各机组组合问题的波动风险;计算期望下行风险时,各最优调度表的利润在各个情景利润下的下行风险的期望值即为各机组组合问题的期望下行风险。
表4给出了所得PBUC问题和SPBUC问题的最优调度表分别在预测电价下和30个电价情景下的利润值以及在不同风险指标下的风险值。PBUC问题在30个电价情景下的利润值是指PBUC问题的最优调度表在30个电价情景下算得的期望利润值,而SPBUC问题在预测电价下的利润值是指SPBUC问题的最优调度表在预测电价(即单个电价情景)下算得的利润值。
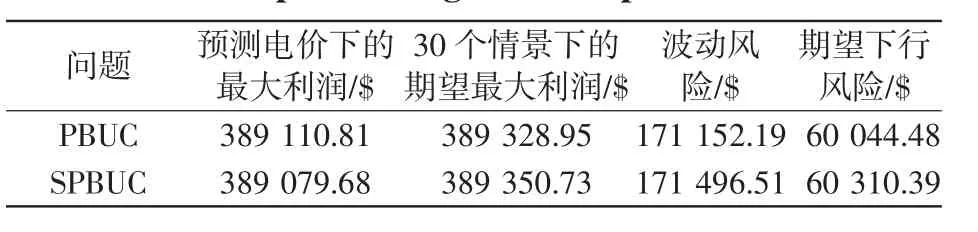
表4 发电利润及风险值比较Tab.4 Comparison ofgeneration profitsand risks
由表4可知,SPBUC问题的最优解在30个情景下的利润比PBUC问题的最优解在预测电价下的利润高239.92$,并且比其在30个情景下的利润值高21.78$,但其期望下行风险和波动风险却比PBUC问题分别高265.91$和344.32$。这说明SPBUC问题的数学模型在提高期望利润的同时也增加了风险,是一种高风险高收益的模型,适合于风险偏好型的决策者,而PBUC问题的数学模型在降低利润的同时也减小了风险,是一种低风险低收益的模型,适合于风险厌恶型的决策者。
为了比较机组效率对发电商的影响,分别将文献[4]中各机组的成本变量值a、Sc、Sh降低20%,其他量保持不变,采用改进粒子群算法重新计算,求得的PBUC问题在预测电价下的最优调度表及SPBUC问题在30个情景电价下的最优调度表分别见表5和表6。各最优调度表分别在预测电价下和30个电价情景下的利润值及在不同风险指标下的风险值见表7。
由表7可知,SPBUC问题的最优解在30个情景下的利润比PBUC问题的最优解在预测电价下的利润高391.41$,并且比其在30个情景下的利润值高89.08$,但其期望下行风险和波动风险却比PBUC问题分别高547.27$和857.43$。同样,该数据说明了SPBUC问题的数学模型适合于风险偏好型的决策者,而PBUC问题的数学模型适合于风险厌恶型的决策者。

表5 成本变量降低20%时PBUC问题的最优调度表Tab.5 Optimalschedule of PBUC problem w ith a 20% decrease in costvariables

表6 成本变量降低20%时SPBUC问题的最优调度表Tab.6 Optimalscheduleof SPBUC problem w ith a 20% decrease in cost variables

表7 成本变量降低20%发电利润及风险值比较Tab.7 Comparison ofgeneration profitsand risksw ith a 20%decrease in costvariables
另一方面,表7中的PBUC问题的最优解与表4中的PBUC问题的最优解相比,其在预测电价下的利润和30个情景下的利润分别增加了23 603.33$和23 687.49$。同时,表7中的SPBUC问题的最优解与表4中的SPBUC问题的最优解相比,其在预测电价下的利润和30个情景下的利润分别增加了23 386.09$和23 754.79$。这说明提高机组效率能给发电商带来显著的经济效益。
5 结语
本文建立了市场环境下的PBUC问题与SPBUC问题的数学模型,并采用改进粒子群算法对这两种机组组合问题数学模型求解。计算结果表明,在不同的风险态度下,发电商应采取不同的机组组合问题数学模型进行求解和决策。最后,通过比较两种机组参数情况下最优调度表的获利情况表明,提高机组效率能给发电商带来显著的经济效益。
[1]Lee F N.Short-term thermal unit commitment-a new method[J].IEEE Trans on Power Systems,1988,3(2):421-428.
[2]SnyderW L Jr,PowellH D,Rayburn JC.Dynamic programming approach to unit commitment[J].IEEE Trans on Power Systems,1987,2(2):339-350.
[3]Zhuang F,Galiana F D.Towards a more rigorous and practical unit commitment by Lagrangian relaxation[J]. IEEE Transon Power Systems,1988,3(2):763-773.
[4]KazarlisSA,BakirtzisAG,PetridisV.A genetic algorithm solution to the unitcommitmentproblem[J].IEEETranson Power Systems,1996,11(1):83-92.
[5]TakritiS,Birge JR,Long E.A stochasticmodel for the unit commitment problem[J].IEEE Trans on Power Systems,1996,11(3):1497-1508.
[6]Shiina T,Birge JR.Stochastic unit commitment problem [J].International Transactions in Operational Research,2002,1252(11):117-123.
[7]熊高峰,聂坤凯,刘喜苹,等(Xiong Gaofeng,Nie Kunkai,Liu Xiping,etal).基于遗传算法的随机机组组合问题求解(GA-based solution to stochastic unit commitmentproblem)[J].电力系统及其自动化学报(Proceeding of the CSU-EPSA),2012,24(5):93-99.
[8]Padhy N P.Unit commitment-a bibliographical survey[J]. IEEETranson Power Systems,2004,19(2):1196-1205.
[9]Padhy Narayana Prasad.Unit commitment problem under deregulated environment-a review[C]//IEEE Power Engineering Society GeneralMeeting.Toronto,Canada:2003.
[10]Baillo A,Ventosa M,Rivier M,et al.Optimal offering strategies for generation companies operating in electricity spotmarkets[J].IEEE Trans on Power Systems,2004,19(2):745-753.
[11]Pereira MV,Granville S,Fampa M,etal.Strategy bidding under uncertainty:a binary expansion approach[J].IEEE Transon Power Systems,2005,20(1):180-188.
[12]Tao L,Shahidehpour M,Zuyi L.Risk-constrained bidding strategywith stochastic unitcommitment[J].IEEETranson Power Systems,2007,22(1):449-458.
[13]Kennedy J,EberhartR.Particle swarm optimization[C]// IEEE InternationalConferenceon NeuralNetworks.Perth,Australia:1995.
[14]Dieu VN,OngsakulW.Enhanced augmented Lagrangian Hopfield network forunitcommitment[J].IEEProceed-ings-Generation,Transmission and Distribution,2006,153(6):624-632.
[15]曾次玲,张步涵(Zeng Ciling,Zhang Buhan).浅析发电公司的竞价策略(A preliminary analysison bidding strategy of power generation companies)[J].电网技术(Power System Technology),2002,26(5):49-53,75.
[16]Kennedy J,EberhartR C.A discrete binary version of the particle swarm algorithm[C]//IEEE International Conference on Systems,Man,and Cybernetics.Orlando,USA:1997.
[17]Zwe-Lee Gaing.Discrete particle swarm optimization algorithm for unit commitment[C]//IEEE Power Engineering Society GeneralMeeting.Toronto,Canada:2003.
[18]刘涌,侯志检,蒋传文(Liu Yong,Hou Zhijian,Jiang Chuanwen).求解机组组合问题的改进离散粒子群算法(Unit commitment via an enhanced binary particle swarm optimization algorithm)[J].电力系统自动化(Automation of Electric Power Systems),2006,30(4):35-39.
[19]PJMMarket.Day-ahead LMP data[EB/OL].http://www. pjm.com/markets-and-operations/energy/day-a-head/lmpda.aspx,2012.
Comparison of Unit Comm itment Problem Considering Price in Markets
XIONGGaofeng,CAIZhenhua,XIEShanghua,LIUman
(CollegeofElectricaland Information Engineering,Hunan University,Changsha410082,China)
To compare themodelofprice-based unit commitmentproblem and themodelofstochastic price based unit commitmentproblem in electric powermarkets,this paper introduces two risk indicators,and adoptsan improved particle swarm optimization to solve these two kinds of unit commitment problem.During the solution,the unit commitmentproblem is decomposed into a two-stage optimization problem.A uniton/off status schedule is determined in the firststage,and the generation outputofeach unit is determined in the second stage.Also,a kind ofminimum up/down repair strategy is introduced.Numerical results indicate that,with different risk attitudes,decision makers should adoptdifferentmathematicalmodelandmake decision accordingly.
price-based unitcommitment(PBUC);stochastic price based unit commitment(SPBUC);risk indicators;improved particle swarm optimization
10.3969/j.issn.1003-8930.2015.04.011
熊高峰(1969—),男,博士,副教授,研究方向为电力系统运行与控制、电力市场。Email:jiaquanx@yahoo.com.cn
2013-04-12;
2013-05-31
TM73
A
1003-8930(2015)04-0061-06
蔡振华(1985—),男,硕士研究生,研究方向为电力系统经济调度。Email:403739239@qq.com
谢上华(1988—),男,硕士研究生,研究方向为电力系统经济调度。Email:553621511@qq.com
